Метод дихотомии

1. Лекция 10

1. Метод дихотомии
2. Метод золотого сечения
3. Сравнение методов одномерной
оптимизации

2. Метод дихотомии

3. Сущность метода дихотомии

Сначала находится середина начального отрезка a;b – точка
c=(a+b)/2. Затем выбирается достаточно малое δ > 0 (параметр метода). О
том, как правильно выбрать этот параметр, увидим чуть позже. Найдем две
симметричные относительно середины отрезка c точки:
a b
a b
x1
δ и x2
δ
2
2
Вычислим значения целевой функции в точках x1 и x2 – f(x1) и f(x2).
Сравнив эти значения, в силу унимодальности функции можно сократить
отрезок неопределенности следующим образом:
если f(x1) ≤ f(x2), то x* [a;x2], и правая граница отрезка b переносится
в точку x2;
если f(x1) > f(x2), то x* [x1;b], и левая граница отрезка a переносится в
точку x1.
На слайде 2 изображен первый случай.
Затем такая же процедура выполняется на новом отрезке, и так далее,
пока длина отрезка неопределенности Δn не станет меньше либо равной
допустимой погрешности приближения ε: Δn = |bn – an| ≤ ε, где an и bn –
концы отрезка неопределенности на n–ой итерации.

4. Свойства метода дихотомии

Длина отрезка неопределенности Δn на n–ой итерации определяется
через концы отрезка неопределенности на предыдущей итерации по
формуле:
b n 1 an 1
Δn
δ
2
Можно показать, что при n→∞ Δn стремится к величине 2δ, оставаясь
больше этой величины. Поэтому добиться при некотором значении n длины
отрезка неопределенности Δn ≤ ε можно лишь выбирая 2δ ≤ ε, откуда δ ≤ ε/2.
Можно взять δ = 0.1ε.
Длину конечного интервала неопределенности Δn можно вычислить
через длину начального интервала Δ0 и количество итераций n по формуле
Δ0 2 δ
Δn
2δ
n
2

5. Свойства метода дихотомии

Положив Δn = ε, можно определить необходимое количество итераций:
Δ 2δ
n log2 0
.
ε 2δ
Выбрав δ = 0.1ε, получим:
Δ 0 0.2 ε
).
n log 2 (
0.8 ε
Например, если начальная длина отрезка равна 1, а допустмая погрешность ε
= 10–6, то n оказывается равным 21, то есть практически таким же, как в
меторе половинного деления при тех же условиях. Это объяснимо, так как
при малой величине δ отрезок неопределенности на каждой итерации
уменьшается практически вдвое.

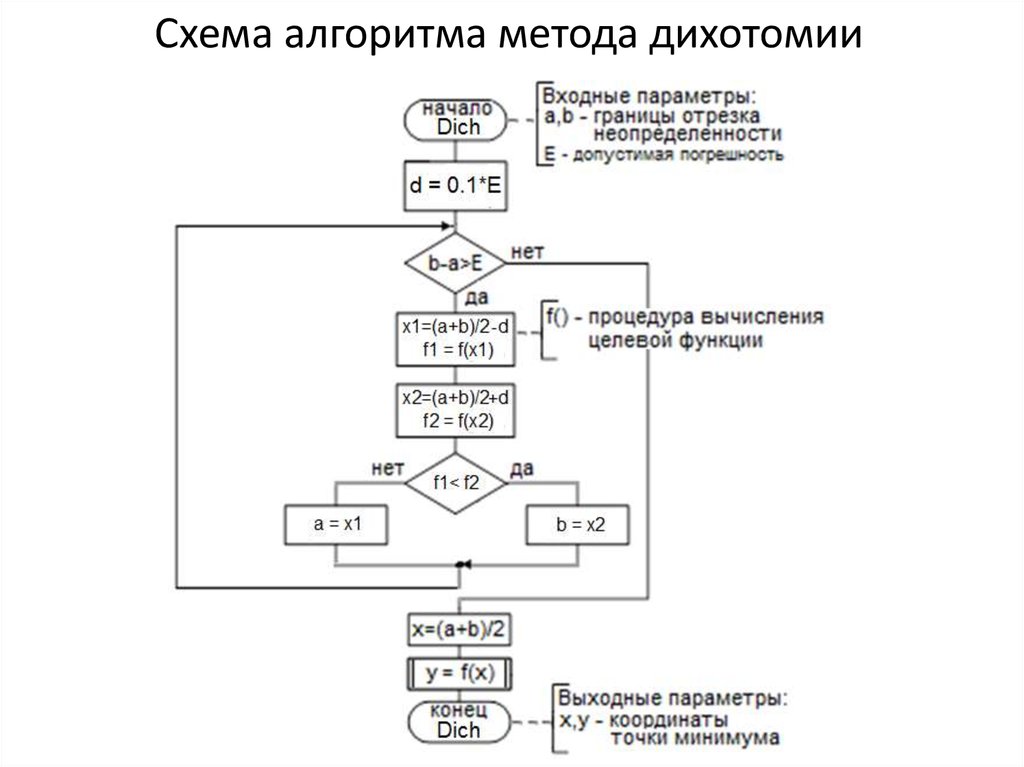
6. Схема алгоритма метода дихотомии

7. Золотое сечение

В основу метода золотого сечения положено разбиение отрезка
неопределенности a;b в соотношении золотого сечения: отношение длины
большей части отрезка ко всей длине отрезка равно отношению длины
меньшей части отрезка к длине его большей части (слайд 7).
l
l1
l1 l2
l l1
l2
l l1 l2
l1 l2
Обозначим z = l2/l1. Сделав подстановки и решив квадратное уравнение
z2 + z – 1 = 0, получим z = (√5-1)/2 ≈ 0.618. Таким образом,
l1 l 2
0.618
l l1
l2
l1
1 0.382
l
l

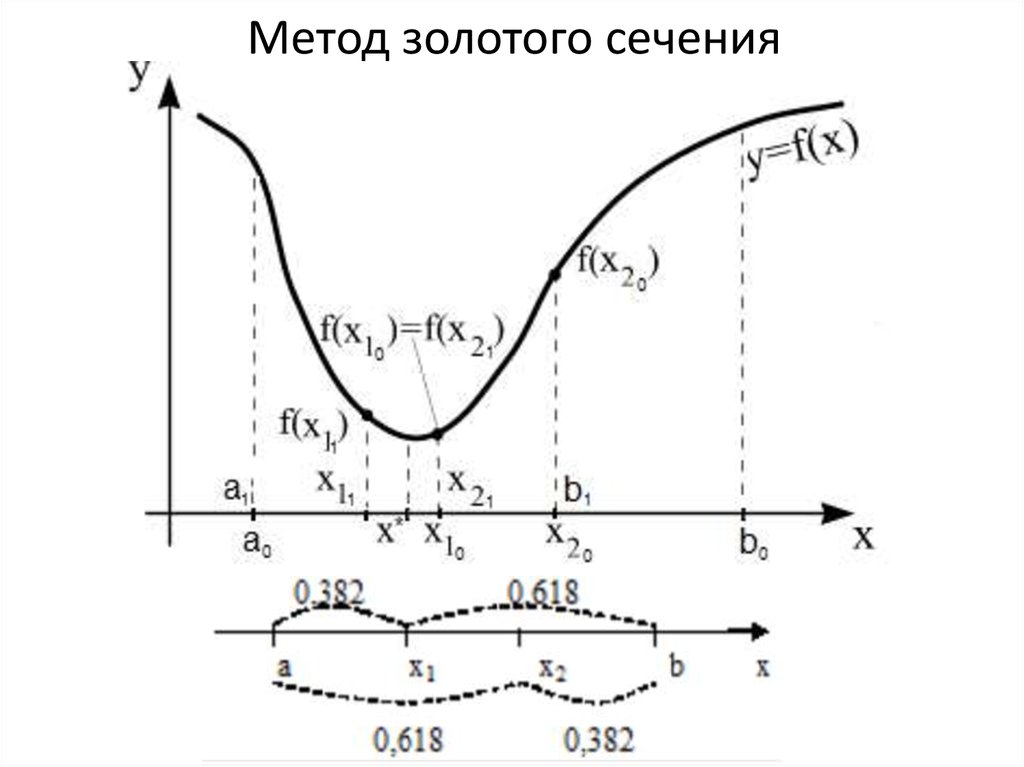
8. Метод золотого сечения

9. Сущность метода золотого сечения

Обозначим k1 = 0.382, k2 = 0.618. Сначала начальный отрезок [a0;b0]
разбивается точками золотого сечения x10 и x20 так, что
x10 = a0 + k1∙( b0 - a0), x20 = a0 + k2∙( b0 - a0)
Затем сравниваются значения функции в этих точках: f(x10) и f(x20).
Если f(x10) < f(x20) (как на рисунке), то в силу унимодальности f(x) точка
минимума x* находится слева от точки x20. В этом случае на следующей
итерации правым концом нового отрезка неопределенности b1 становится
точка x20. При этом левая граница нового отрезка остается на месте: a1 = a0.
Нетрудно убедиться, что точка x10 осуществляет золотое сечение не
только отрезка [a0;b0], но и нового отрезка [a1;b1]. Однако на новом отрезке
она становится правой точкой золотого сечения: x21 = x10 со значением
функции f(x21) = f(x10). Левая же точка вычисляется заново:
x11 = a1 + k1∙( b1 – a1).
В противном случае на следующей итерации левым концом нового
отрезка a становится точка x1 предыдущего отрезка, правый конец отрезка b
сохраняет свое положение, левой точкой x1 нового отрезка становится правая
точка предыдущего отрезка, а правая точка x2 вычисляется заново. Такой
случай будет иметь место на следующем шаге для рисунка на слайде 8.

10. Свойства метода золотого сечения

Таким образом, значение целевой функции на каждой итерации (кроме
первой) вычисляется только один раз. Итерации сужения отрезка
неопределенности продолжаются до тех пор, пока длина отрезка
неопределенности Δn не станет меньше либо равной допустимой
погрешности приближения ε: Δn = |bn – an| ≤ ε, где an и bn – концы отрезка
неопределенности на n–ой итерации.
После каждой итерации длина отрезка неопределенности сокращается
в l/l1 раз (примерно 1.618 раза). Длина конечного отрезка неопределенности
n = 0.618n 0, где 0= (b0-a0) – начальная длина отрезка. Положив Δn = ε,
можно определить необходимое количество итераций:
ε
lg( )
lgΔ0 lgε
Δ0
n
lg 0.618
0.21
Например, если начальная длина отрезка равна 1, а допустимая погрешность
ε = 10–6, то n оказывается равным 29, что при тех же условиях примерно в
полтора раза больше, чем в методах половинного деления и дихотомия

11. Схема алгоритма метода золотого сечения

12. Основные характеристики методов одномерной оптимизации

Метод
Деления отрезка
пополам
Дихотомии
Золотого сечения
Коэффициент сужения
отрезка
неопределенности
Количество вычислений
функции на каждой
итерации
0.5
1 или 2
0.5 + δ
0.618
2
1
Критерием
сравнения
методов
одномерной
оптимизации может служить эффективность –
количество вычислений функции, требуемое для
достижения
требуемого
сужения
отрезка
неопределенности. Можно говорить, наоборот, о
коэффициенте сужения отрезка неопределенности в
зависимости от количества вычислений целевой
функции.

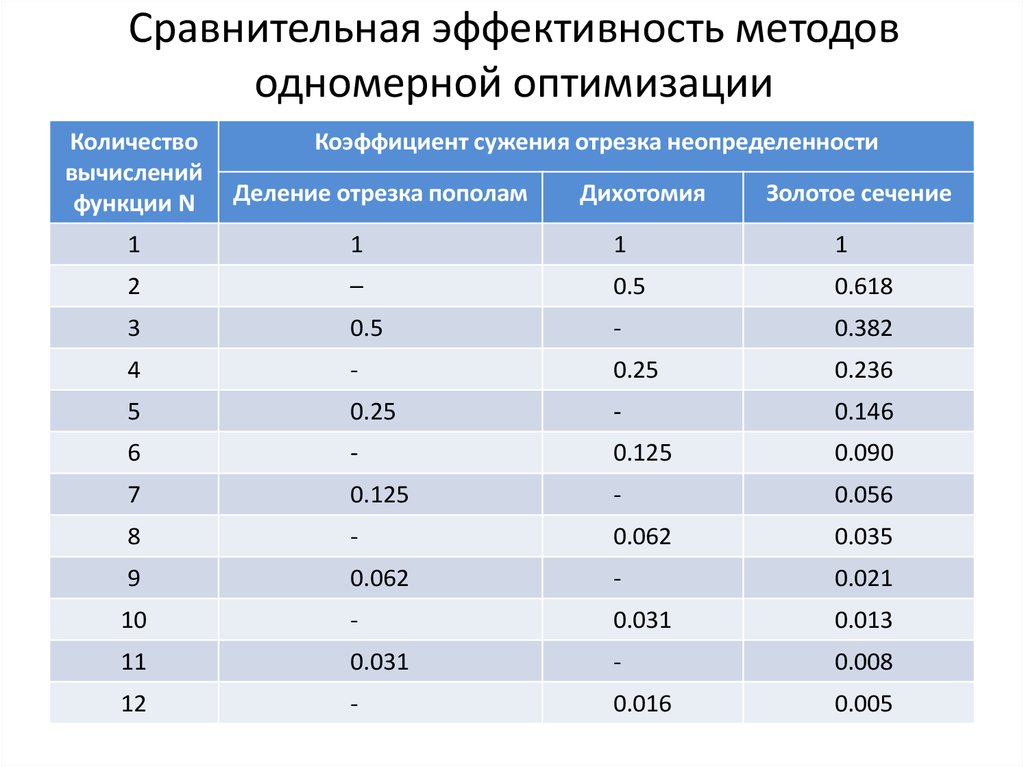
13. Сравнительная эффективность методов одномерной оптимизации

Количество
вычислений
функции N
Коэффициент сужения отрезка неопределенности
Деление отрезка пополам
Дихотомия
Золотое сечение
1
1
1
1
2
–
0.5
0.618
3
0.5
-
0.382
4
-
0.25
0.236
5
0.25
-
0.146
6
-
0.125
0.090
7
0.125
-
0.056
8
-
0.062
0.035
9
0.062
-
0.021
10
-
0.031
0.013
11
0.031
-
0.008
12
-
0.016
0.005