Похожие презентации:
Одномерная оптимизация. Методы классического анализа
1. 2. Одномерная оптимизация
2.1. Методы классического анализаРассмотрим задачу минимизации функции одной
переменной f (x) на множестве X R1 :
min
x X
f ( x),
где R1 - множество действительных чисел одномерного
пространства.
а) глобальные и локальные минимумы
*
Определение 1. Точка x доставляет глобальный минимум
*
*
функции f (x) на множестве X , если x X и f ( x ) f ( x)
для всех x X
2.
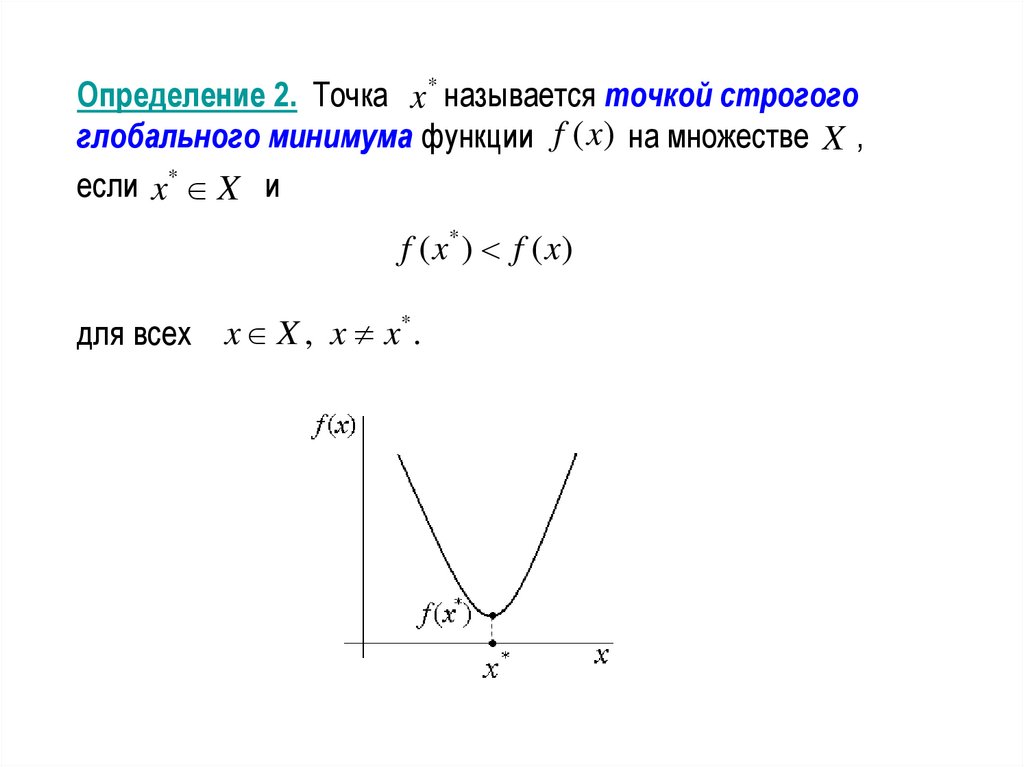
Определение 2. Точка x * называется точкой строгогоглобального минимума функции f (x) на множестве X ,
если x* X и
f ( x* ) f ( x)
для всех x X , x x* .
3.
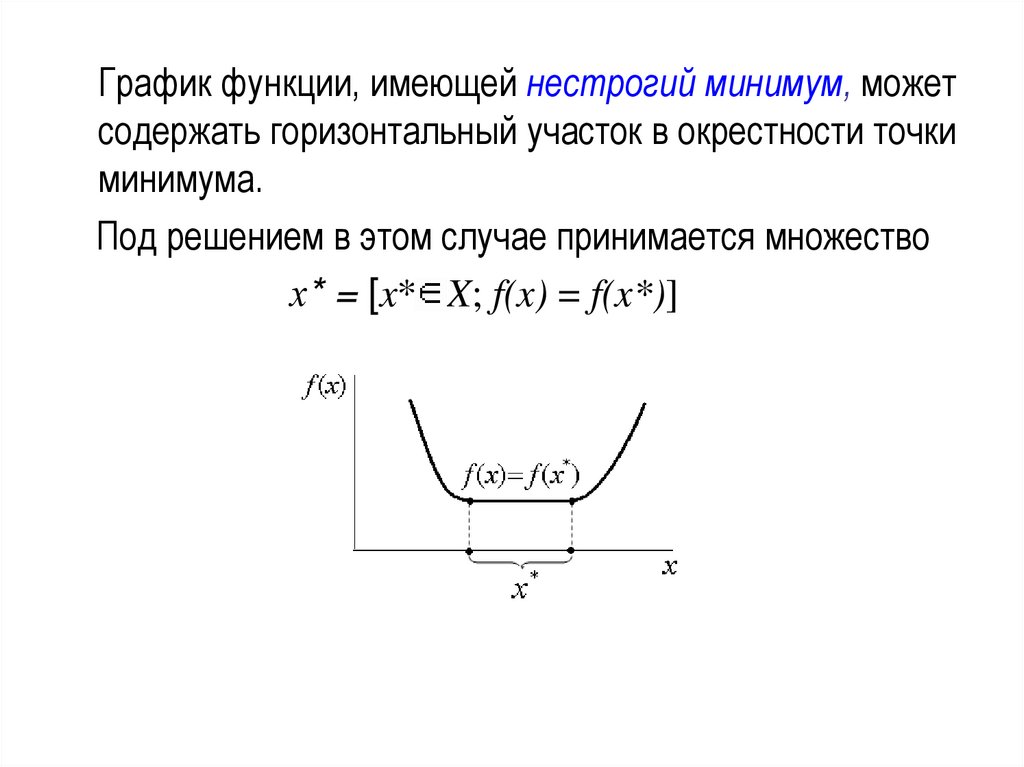
График функции, имеющей нестрогий минимум, можетсодержать горизонтальный участок в окрестности точки
минимума.
Под решением в этом случае принимается множество
х* = [x* X; f(x) = f(x*)]
4.
Определение 3. Точка x0 X называется точкойлокального минимума функции f (x) , если существует
такое число 0 , что для всех x x0 , x X
удовлетворяющих условию x x0
выполнено неравенство
f ( x0 ) f ( x).
(2.1)
Если неравенство (2.1) – строгое, то точку x 0
называют точкой строгого локального минимума
функции f (x ).
5.
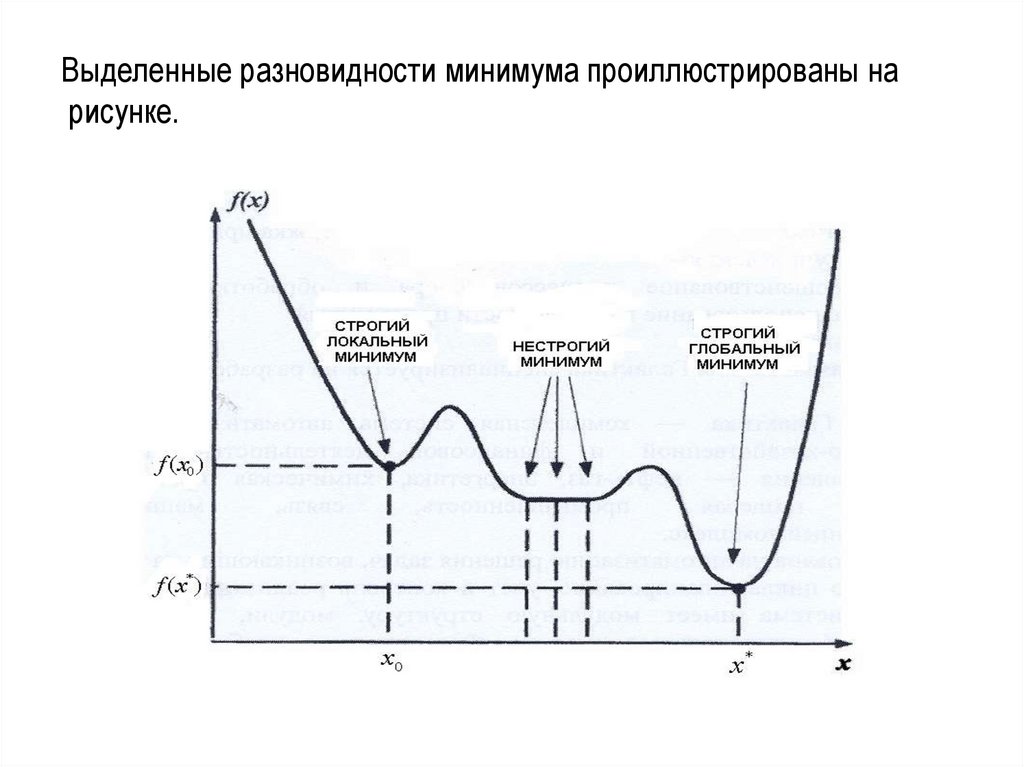
Выделенные разновидности минимума проиллюстрированы нарисунке.
6. в) алгоритм нахождения точки минимума с использованием производной
1.2.
Найти первую производную функции f (x ).
Найти критические (стационарные) точки функции, для этого:
- найти корни уравнения f ( x) 0 ;
- найти точки, в которых функция f (x ) не существует.
3. Исследовать поведение знака f (x ) в окрестности каждой
критической точки: если при переходе слева направо через
критическую точку функция меняет знак, то такая критическая
точка является точкой экстремума:
- точкой максимума, если знак меняется с плюса на минус;
- точкой минимума, если знак меняется с минуса на плюс.
7. г) достаточные условия экстремума
Если функция f (x) дважды непрерывно дифференцируема, тодостаточным условием минимума является положительность, а
максимума отрицательность второй производной f ( x* ).
Если существует производная f ( n ) ( x) и если
f ( x* ) f ( x* ) . . . f ( n 1) ( x* ) 0 ,
*
x
то функция f (x) имеет в точке
:
- минимум при n четном и f ( n) ( x* ) 0 ;
- максимум при n четном и f ( n) ( x* ) 0.
*
f
(
x
) в точке x * имеет точку
Если n нечетно, то функция
перегиба.
8.
Пример 2.1. Решить пример 1.1, используя необходимыеи достаточные условия экстремума.
V0
2
S
(
r
)
2
(
r
).
Решение. Целевая функция имеет вид
r
Найдем стационарные точки функции S (r )
V0
V0
*
3
S (r ) 2 (2r
) 0 r
2
2
r
Так как функция дважды непрерывно дифференцируема, то
достаточные условия экстремума исследуем с помощью второй
производной
2V0
S (r ) 2 (2
).
3
r
Так как S (r * ) 2 (2
2V0 2
) 12 0, то в точке
V0
минимум целевой функции.
r
*
достигается
9.
Из условияV0 r 2 h
найдем:
2
2
3
V
V
4
V
2
*
0
0 3
0
3
h
* 2
2
3
(r )
V0
V0
3
4 V0
8 V0
V0
*
3
2
2r ,
2
2
3
т.е. высота цилиндрического бака должна быть равна
диаметру основания бака.
10. 2.2. Численные методы поиска экстремума функции одной переменной
2.2.1. Постановка задачи.Будем предполагать, что в пределах отрезка a, b
функция f (x) унимодальна, т.е. на данном отрезке имеет только
один минимум.
*
x
Другими словами, если
– единственная точка
минимума на отрезке , то f (x) является унимодальной на данном
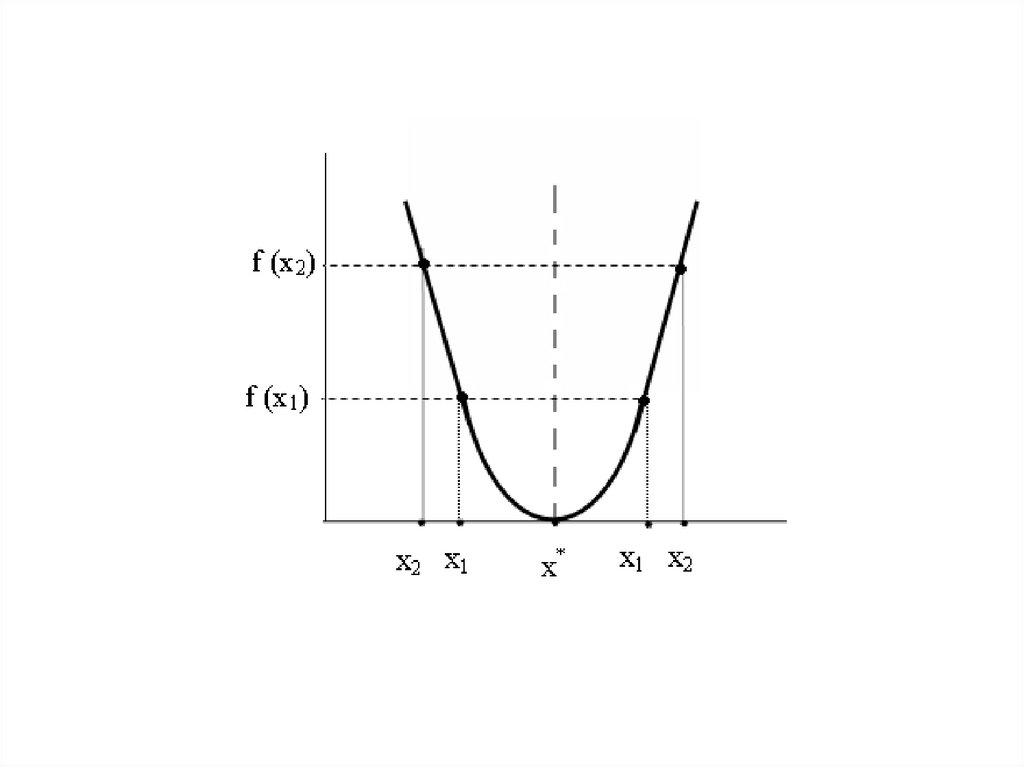
отрезке тогда и только тогда, когда для любых двух точек отрезка
x1 и x 2 взятых по одну сторону от точки минимума x *
соответствует меньшее значение функции, т.е. как при x* x1 x2 ,
*
так и при x x1 x2 справедливо неравенство
f ( x* ) f ( x1 ) f ( x2 ).
11.
12.
Унимодальная функция может быть непрерывной, разрывнойили дискретной.
Для проверки унимодальной функции на практике обычно
используют следующий критерий:
если функция f (x) дважды дифференцируема на отрезке a, b и
f ( x) 0 в любой точке этого отрезка, то f (x) унимодальная
функция на отрезке a,b .
Заметим, что f ( x) 0 определяет множество точек, на котором
функция является выпуклой вниз.
Пример 2.2. Для функции f ( x) 2 x 2 ln x найти отрезок, на
котором функция унимодальна.
13.
Решение.Функция f (x) определена при x 0.
Найдем ее производные:
1
f ( x) 4 x
x
1
при
x (0; )
f ( x) 4 2 0
x
Следовательно, функция
Первая производная
Следовательно x 0,5
f (x) унимодальна на интервале (0, ).
f ( x) 0 при x 0,5.
- точка локального минимума.
14. 2.2.2. Стратегии поиска
Существуют две принципиально различныестратегии выбора точек, в которых производится
вычисление значений целевой функции.
Пассивная стратегия - все точки задаются заранее,
до начала вычислений.
Последовательная стратегия - точки выбираются
последовательно в процессе поиска с учетом
результатов предыдущих вычислений.
15.
Последовательную стратегию можнореализовать двумя способами:
построением последовательности
вложенных в друг друга интервалов, каждый
из которых содержит точку минимума;
применением квадратичной и кубической
интерполяции, где по нескольким
вычисленным значениям функции строятся
интерполяционный многочлен, а его минимум
указывает на очередное приближение
искомой точки экстремума.
16.
Алгоритм последовательной стратегииВыбор начального интервала [a, b] изменения параметра ,
называемого интервалом неопределенности. Границы
интервала
выбираются таким образом, чтобы функция была унимодальной.
Для выбора начального интервала неопределенности можно
применить алгоритм Свенна.
Уменьшение интервала неопределенности.
Проверку условия окончания процесса вычислений. Поиск
заканчивается, когда длина текущего интервала
неопределенности [ak , bk ] будет меньше заданной точности
вычислений >0, т.е. bk ak .
17. Прием уменьшения интервала неопределенности
Пусть функция f (x ) унимодальна на интервале [ a, b]и ее минимум достигается в точке x* [a, b]. Возьмем две
произвольные точки x1 и x 2 , расположенные на
интервале таким образом, что x1 x2 . Сравнивая
значения функции f ( x1 ), f ( x2 ) в этих точках, можно
x
сузить интервал неопределенности
следующим образом:
• если f ( x1) f ( x2 ), то точка минимума лежит на интервале [a, x 2 ].
*
18.
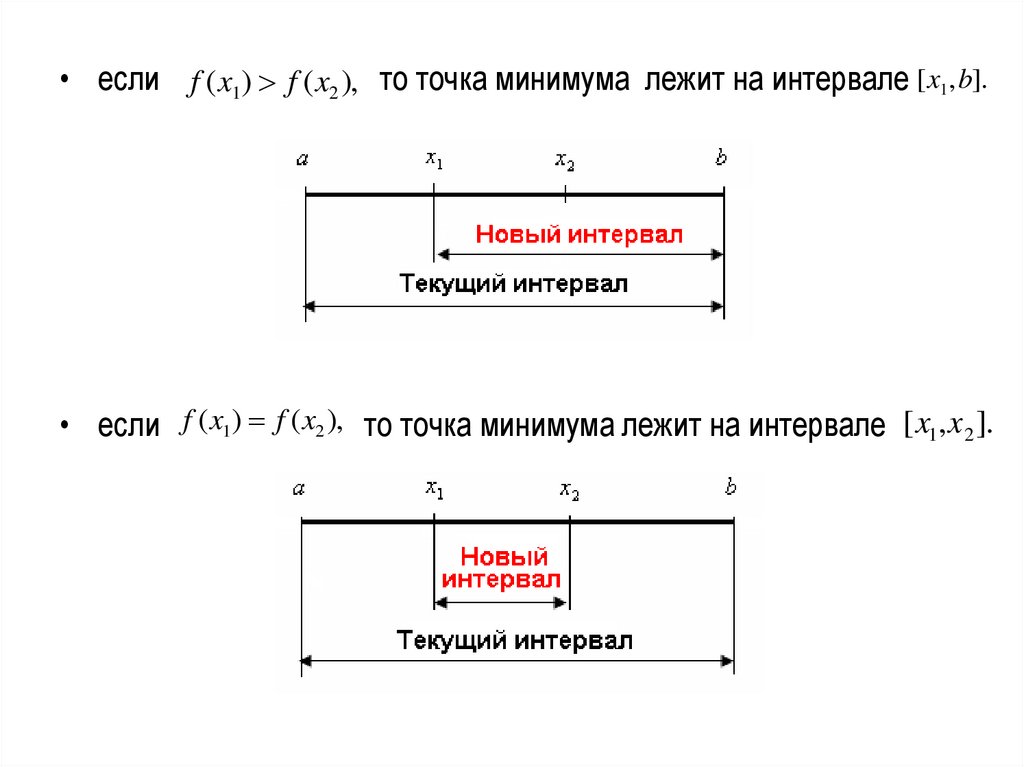
• если f ( x1) f ( x2 ), то точка минимума лежит на интервале [ x1, b].• если f ( x1) f ( x2 ), то точка минимума лежит на интервале [ x1, x 2 ].
19.
Рассмотрим наиболее распространенные в
практике следующие приближенные методы поиска
минимума:
метод равномерного поиска;
метод дихотомии;
метод деления интервала пополам;
метод золотого сечения;
метод Фибоначчи;
метод квадратичной интерполяции.
20.
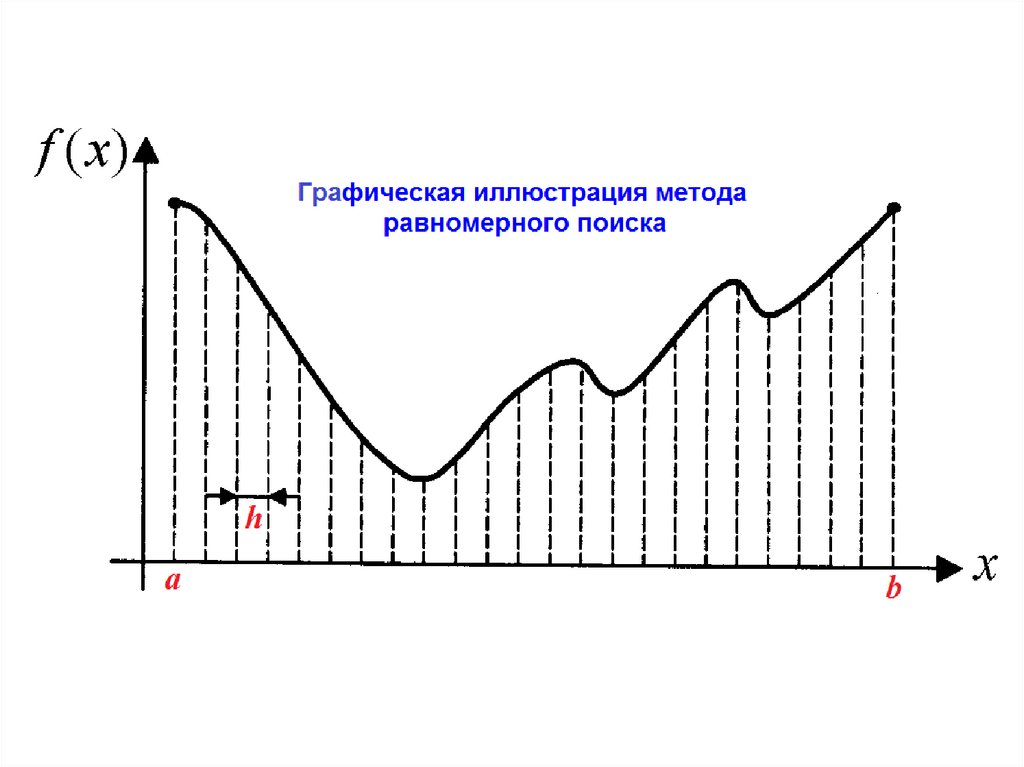
2.2.3. Метод равномерного поискаМетод относится к пассивным стратегиям.
Задается начальный интервал неопределенности a, b
и количество n вычислений целевой функции f (x ).
Вычисляются значения целевой функции f ( xi ) в
равноотстоящих друг от друга точках
b a
xi a ih a i
, i 0, n.
n
21.
*Среди точек xi находится точка x , в которой
целевая функция принимает наименьшее значение
f ( x* ) min f ( xi ).
0 i n
Эффективность метода невелика и вычисляется по
формуле
2
.
n 1
Например, для достижения точности 0.01 ,
потребуется вычислить целевую функцию в 199 точках, а
при 0.001 в 1999 точках.
Преимущество – возможность определения глобального
экстремума.
22.
23.
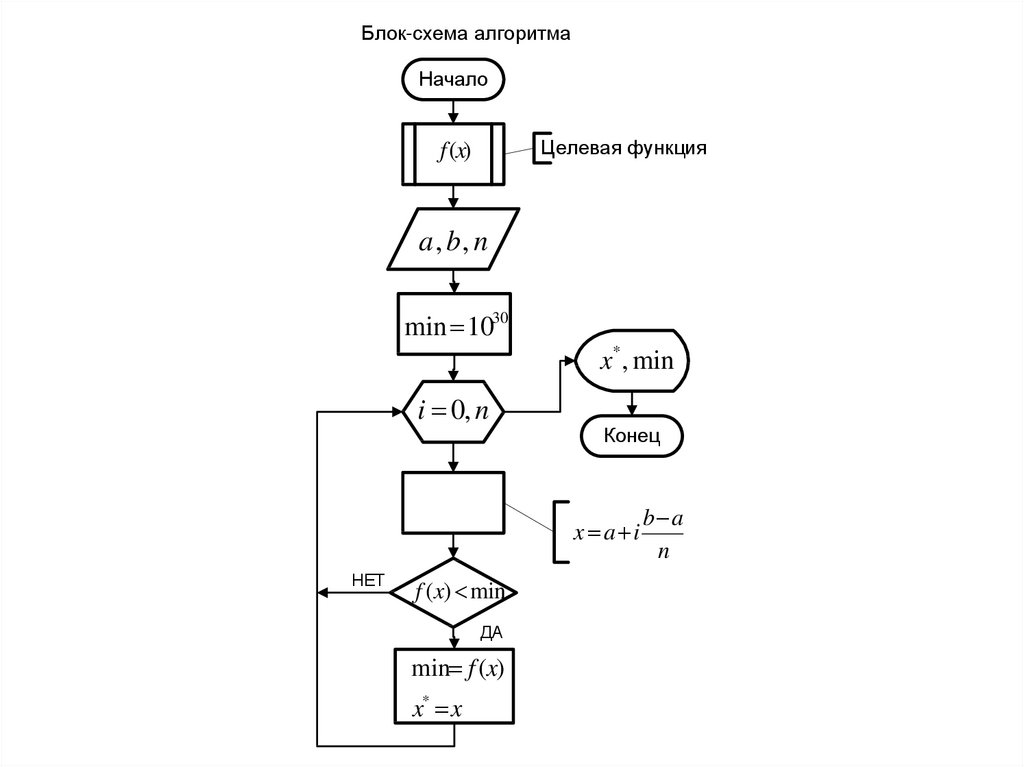
Блок-схема алгоритмаНачало
Целевая функция
f (x)
a , b, n
min 1030
x* , min
i 0, n
Конец
x a i
НЕТ
f (x) min
ДА
min f (x)
x* x
b a
n
24. 2.2.4. Метод дихотомии
Метод относится к последовательным стратегиям.Задается начальный интервал неопределенности a, b и
требуемая точность поиска .
Делится интервал поиска пополам
a b
x
2
и вычисляются две абсциссы симметрично расположенные
относительно точки x :
x1 x ; x2 x ,
2
2
где 0 - величина различимости точек ( ).
25.
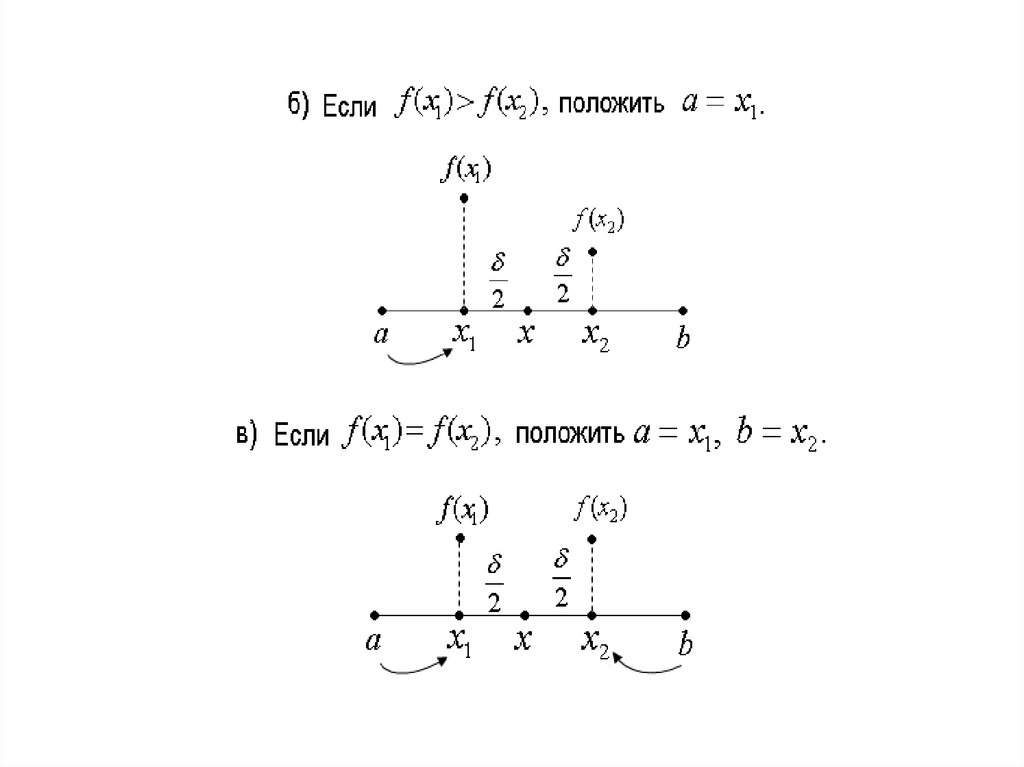
Вычисляются функции f ( x1 ) и f ( x2 ). Сравниваютсяполученные значения и находится новый уменьшенный
интервал неопределенности:
26.
27.
Затем снова вычисляются координаты x1 и x2и продолжается поиск.
За оценку прекращения поиска принимают b a ,
а за минимальное значение
a b
x
.
2
*
За одну итерацию интервал неопределенности
уменьшается примерно в два раза. За n итераций
длина интервала будет примерно равна
b a
n
2
28.
Точность нанеравенством
n м шаге вычислений определяется
b a
n
2
Отсюда следует, что для достижения точности
потребуется
ln[( b a) / ]
n
.
ln 2
итераций.
На каждой итерации целевая функция вычисляется
дважды.
29.
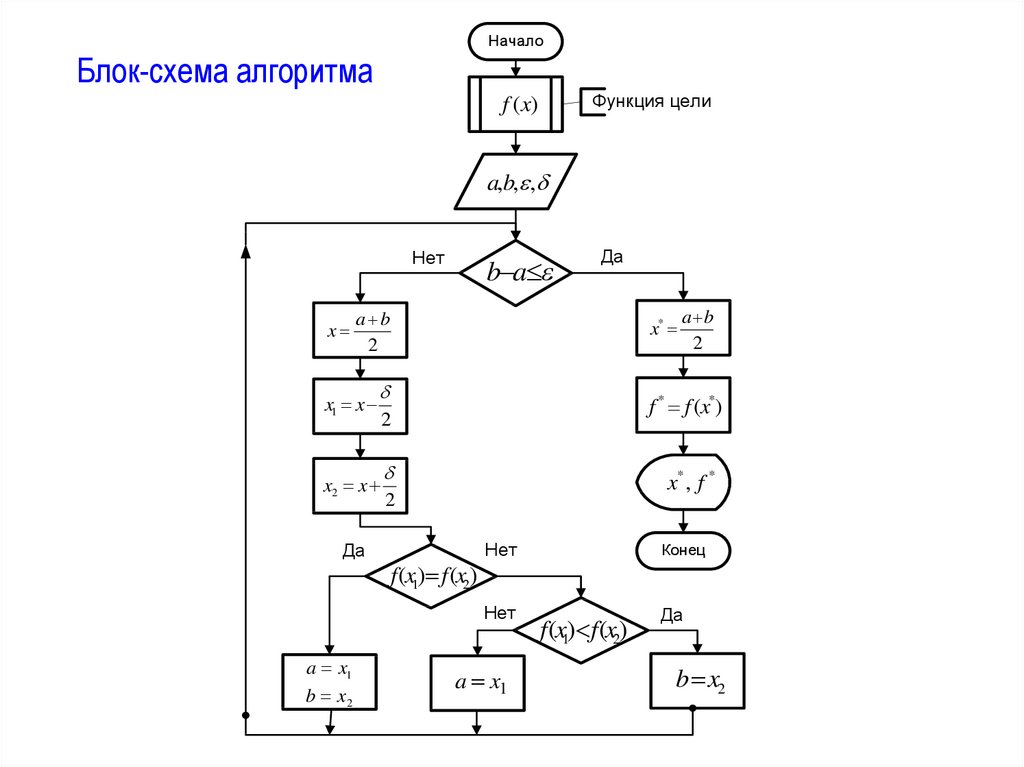
НачалоБлок-схема алгоритма
Функция цели
f (x)
a,b, ,
Нет
x
b a
a b
2
x1 x
Да
x*
x2 x
b x2
a b
2
f * f (x*)
2
x* , f *
2
Нет
Конец
f (x1) f (x2)
Нет
a x1
Да
a x1
f (x1) f (x2)
Да
b x2




















 Математика
Математика








