Похожие презентации:
Основные понятия и законы электрических и магнитных цепей, физические основы электротехники
1. 1. Основные понятия и законы электрических и магнитных цепей, физические основы электротехники
1.1 Физические основы электротехники1.2 Элементы электрических цепей
1.3 Топологические понятия
1.4 Основные законы электрических цепей
1.5 Основные законы магнитных цепей
2. 1.1 Физические основы электротехники
1.1.1 Связь между электрическими и магнитными явлениямиСила Лоренца
F F1 F2 qE q vB
Напряжённость электрического поля
E
F1
q0
F2 qvBsin
Индукция магнитного поля
F
B 2
qv
Тл
Н/Кл, В/м
3.
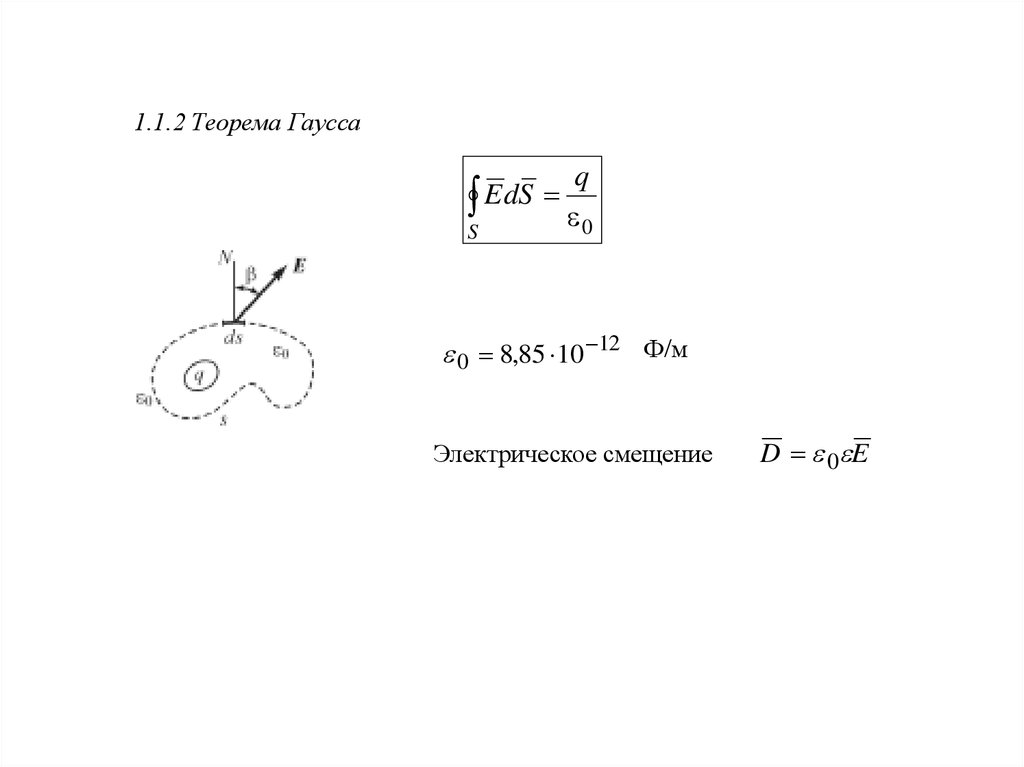
1.1.2 Теорема ГауссаE dS
S
q
0
0 8,85 10 12 Ф/м
Электрическое смещение
D 0 E
4.
1.1.3 Электрические токи проводимости, переноса, смещения. Принципнепрерывности электрического тока
Ток проводимости
dq
i
dt
Модуль вектора плотности тока
Закон Ома
1
i
jdS
S
j
di
dS
А/м2
j E
- удельная электрическая проводимость вещества, См/м
- удельное электрическое сопротивление проводника, Ом·м
E j
5.
Плотность тока смещенияПолный электрический ток
Плотность полного тока
dD
jcм
dt
i
dq d
D dS
dt dt S
j jсм
Принцип непрерывности электрического тока
i dS 0
S
6.
1.1.4 Электрическое напряжение, потенциал, ЭДСЭлектрическое напряжение
B
B
A
A
u AB E cos dl E dl
Электрический потенциал
P
P
E dl U A U x, y, z
U P E dl 0
P
A
Электрическая ёмкость
Для плоского конденсатора
Условие действия ЭДС
C
q1
q2
U1 U 2 U 2 U1
С
0 S
d
Edl e 0
Ф
7.
1.1.5 Магнитный поток. Закон электромагнитной индукцииМагнитный поток
Ф B cos dS B dS
S
Вб
S
Принцип непрерывности магнитного потока
B dS
0
S
dФ
e E dl
dt
Закон электромагнитной индукции
Потокосцепление
ЭДС самоиндукции
wФ
eL L
Индуктивность контура (катушки)
e
di
dt
d
dФ
w
dt
dt
w2 S
L 0
l
Li
8.
1.2 Элементы электрических цепей1.2.1 Основные понятия
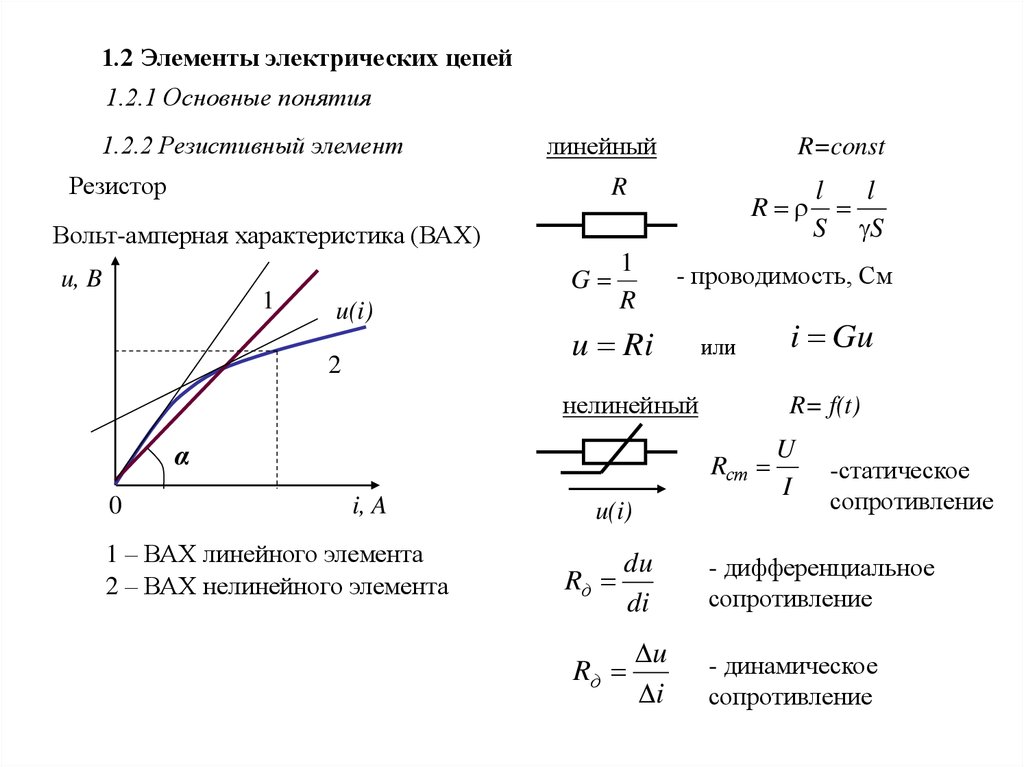
1.2.2 Резистивный элемент
Резистор
линейный
R=const
R
R
Вольт-амперная характеристика (ВАХ)
u, B
1
G
u(i)
2
1
R
- проводимость, См
u Ri
или
нелинейный
α
0
1 – ВАХ линейного элемента
2 – ВАХ нелинейного элемента
u(i)
Rд
du
di
Rд
u
i
i Gu
R= f(t)
Rст
i, A
l
l
S S
U
I
-статическое
сопротивление
- дифференциальное
сопротивление
- динамическое
сопротивление
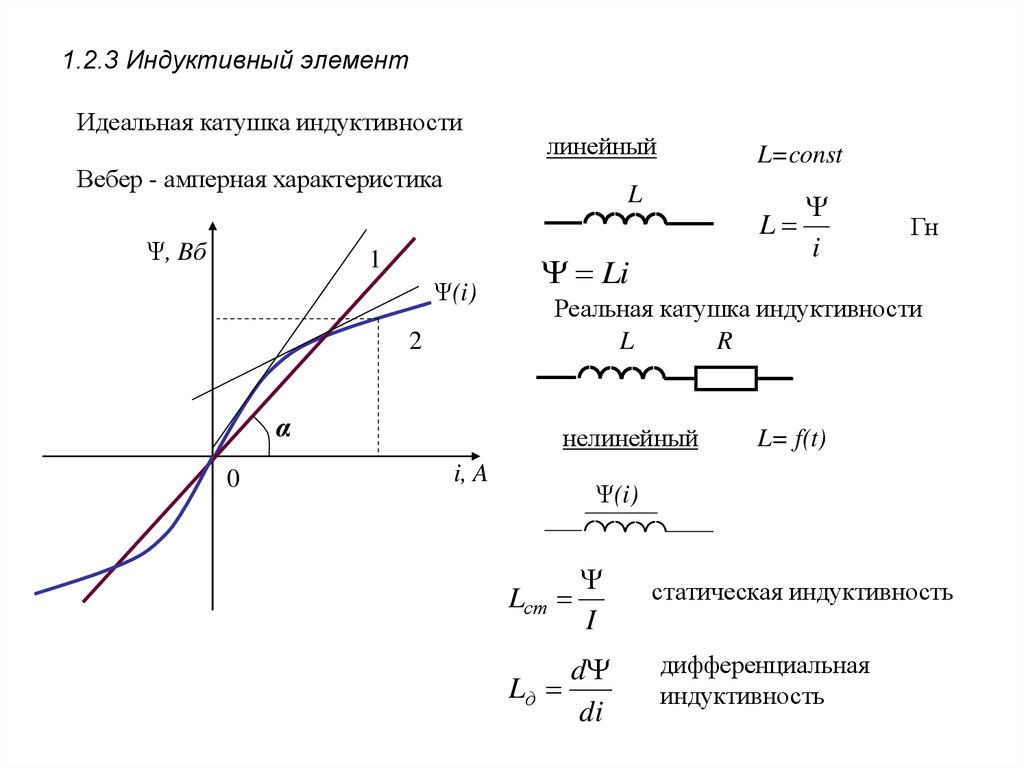
9. 1.2.3 Индуктивный элемент
Идеальная катушка индуктивностилинейный
Вебер - амперная характеристика
Ψ, Bб
L
1
Ψ(i)
2
α
0
L=const
L
Li
i
Гн
Реальная катушка индуктивности
L
R
нелинейный
i, A
L= f(t)
Ψ(i)
Lст
I
d
Lд
di
статическая индуктивность
дифференциальная
индуктивность
10.
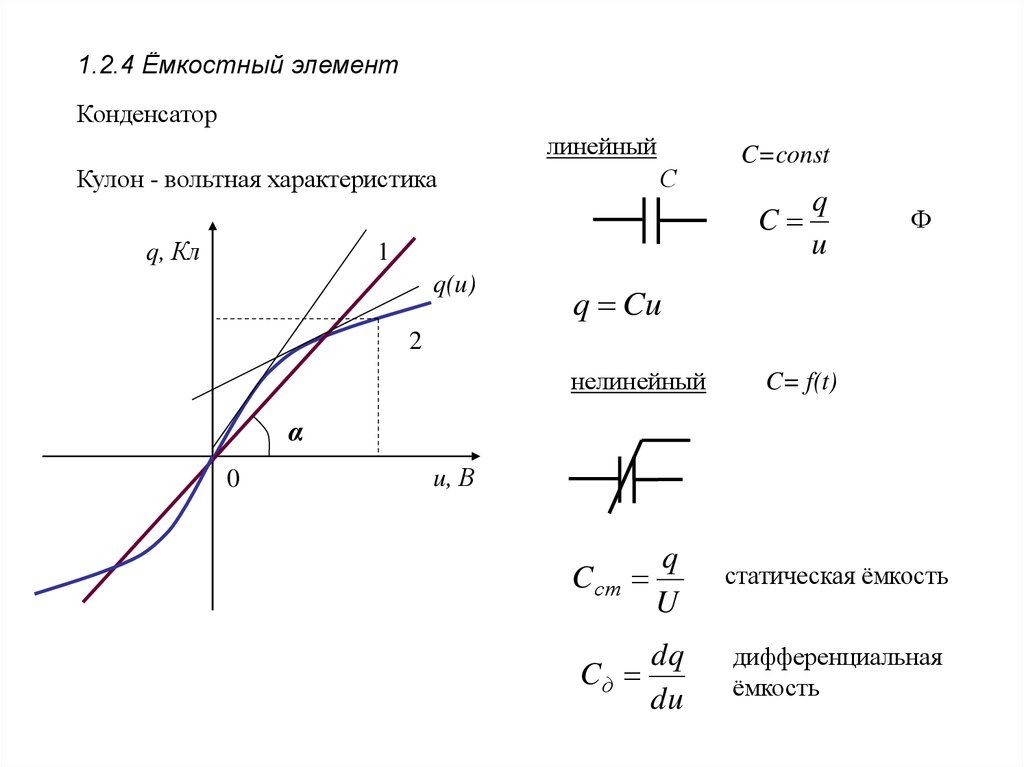
1.2.4 Ёмкостный элементКонденсатор
линейный
Кулон - вольтная характеристика
С
C=const
C
q, Кл
1
q(u)
q
u
Ф
q Cu
2
нелинейный
C= f(t)
α
0
u, В
q
U
статическая ёмкость
dq
Cд
du
дифференциальная
ёмкость
Cст
11. 1.2.5 Источники электрической энергии
IВнешняя характеристика
источника
A
И
U
V
RH
U
а – режим холостого хода
I=0;
UXX а
m
U=UXX
b – режим короткого замыкания
U=0;
n
I=IКЗ
b
0
U=UXX – RBH I
IКЗ
RBH =UXX / IКЗ
I
12.
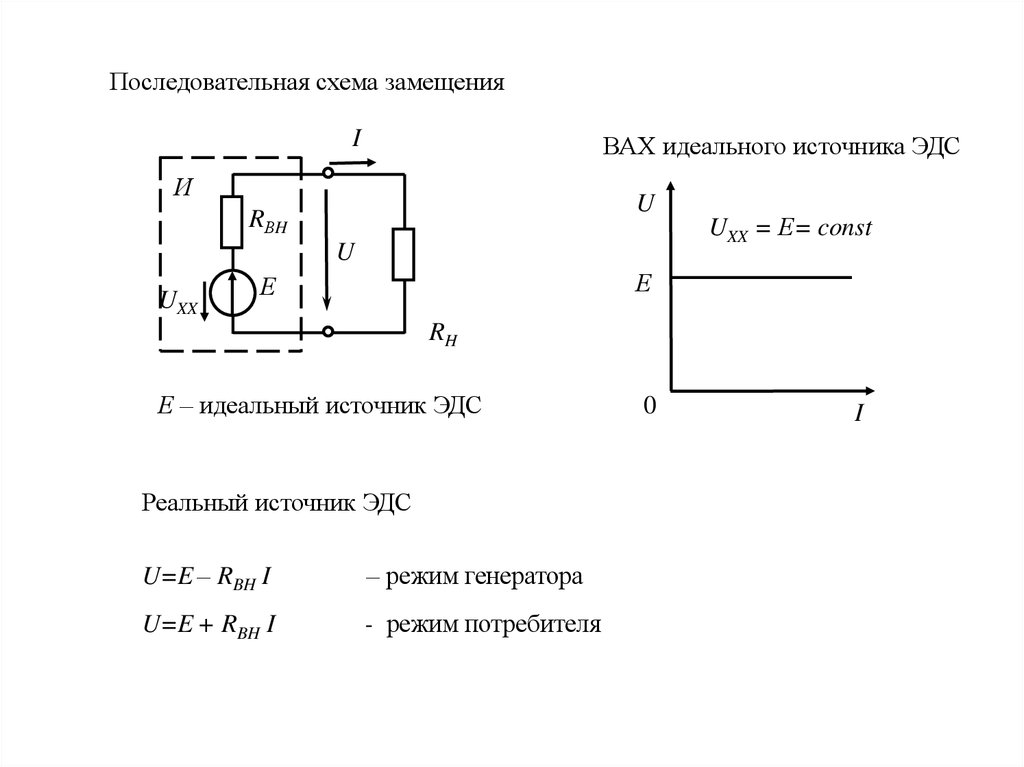
Последовательная схема замещенияI
ВАХ идеального источника ЭДС
И
U
RВH
U
UXX
UXX = Е= const
Е
Е
RH
Е – идеальный источник ЭДС
Реальный источник ЭДС
U=E – RBH I
– режим генератора
U=E + RBH I
- режим потребителя
0
I
13.
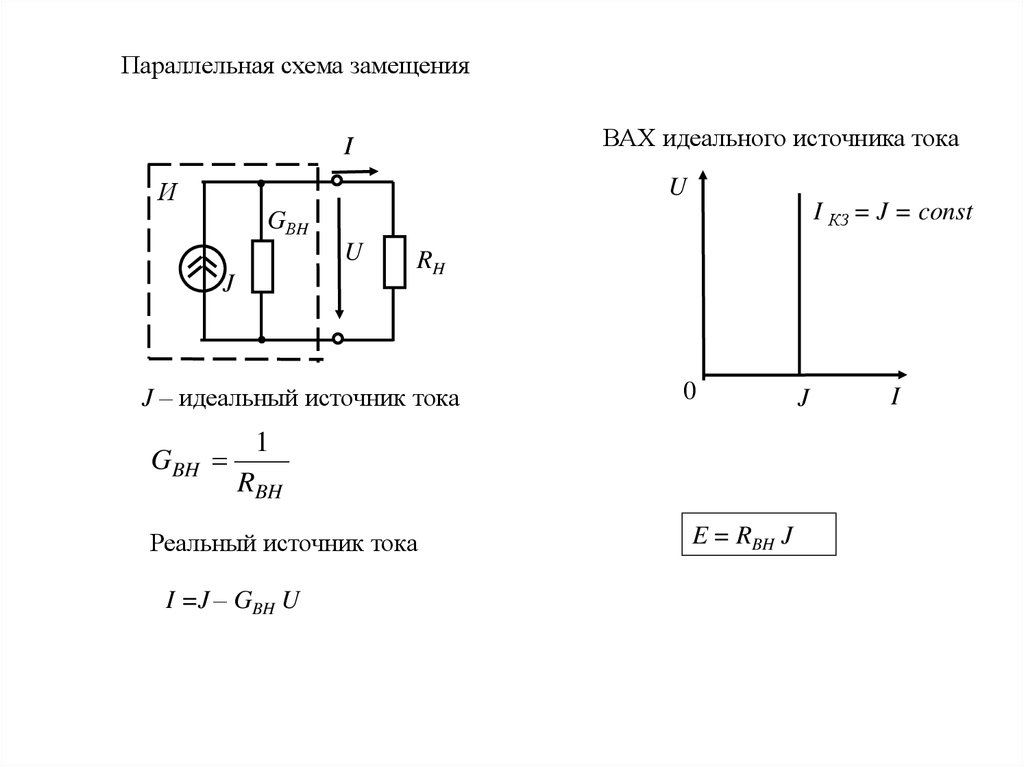
Параллельная схема замещенияВАХ идеального источника тока
I
И
U
I КЗ = J = const
GВH
U
J
RH
J – идеальный источник тока
GBH
0
1
RBH
Реальный источник тока
I =J – GBH U
E = RBH J
J
I
14.
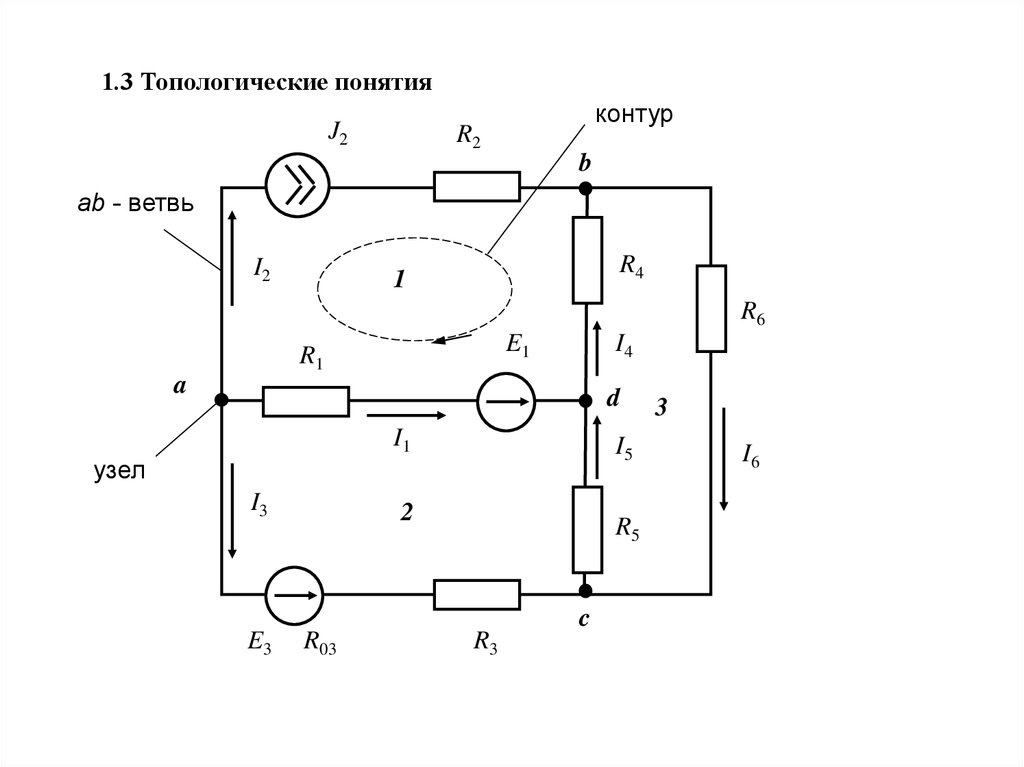
1.3 Топологические понятияJ2
контур
R2
b
ab - ветвь
I2
R4
1
R6
E1
R1
I4
a
d
I1
узел
I3
E3
I5
2
R03
R5
R3
c
3
I6
15.
1.4 Основные законы электрических цепейЗакон Ома
для контура
для участка цепи
U
I ;
R
1 закон Кирхгофа
I
k
k
0
I
U 1 2 E
E
RЭКВ
2 закон Кирхгофа
I
k
Rk Ei
k
U k 0
k
i
16.
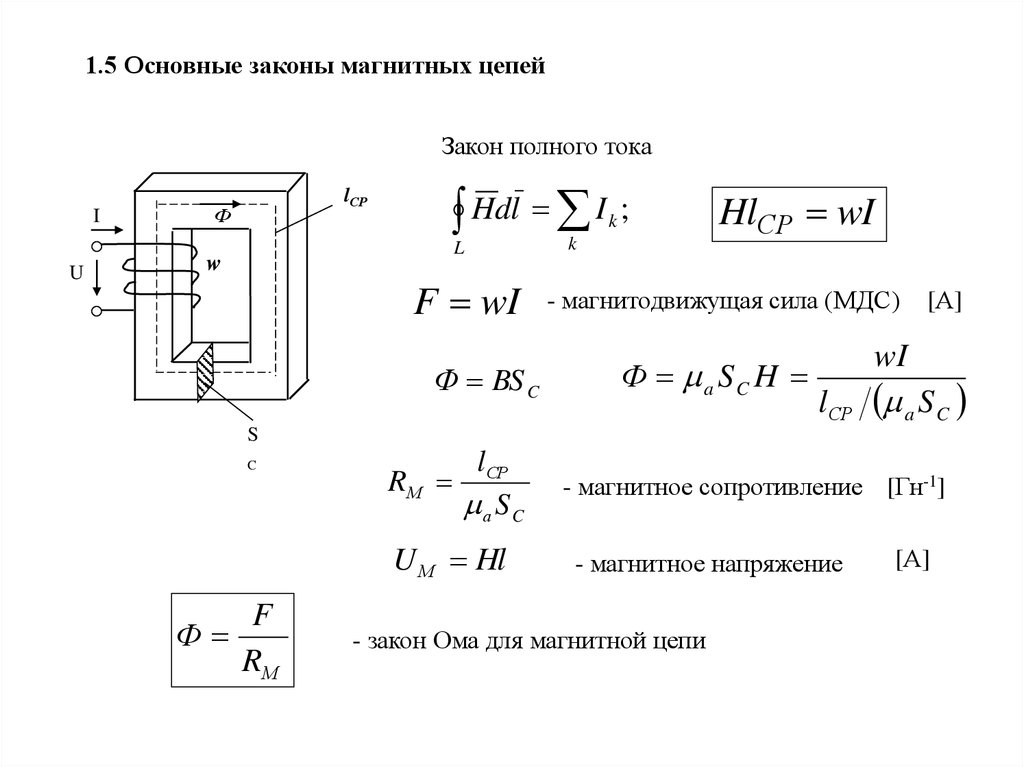
1.5 Основные законы магнитных цепейЗакон полного тока
I
U
lСР
Ф
Hdl I ;
k
L
w
F wI
Ф BS C
k
HlСР wI
- магнитодвижущая сила (МДС)
Ф a SC H
[А]
wI
lСР a S C
S
C
lСР
RМ
а SC
U М Hl
F
Ф
RМ
- магнитное сопротивление [Гн-1]
- магнитное напряжение
- закон Ома для магнитной цепи
[А]
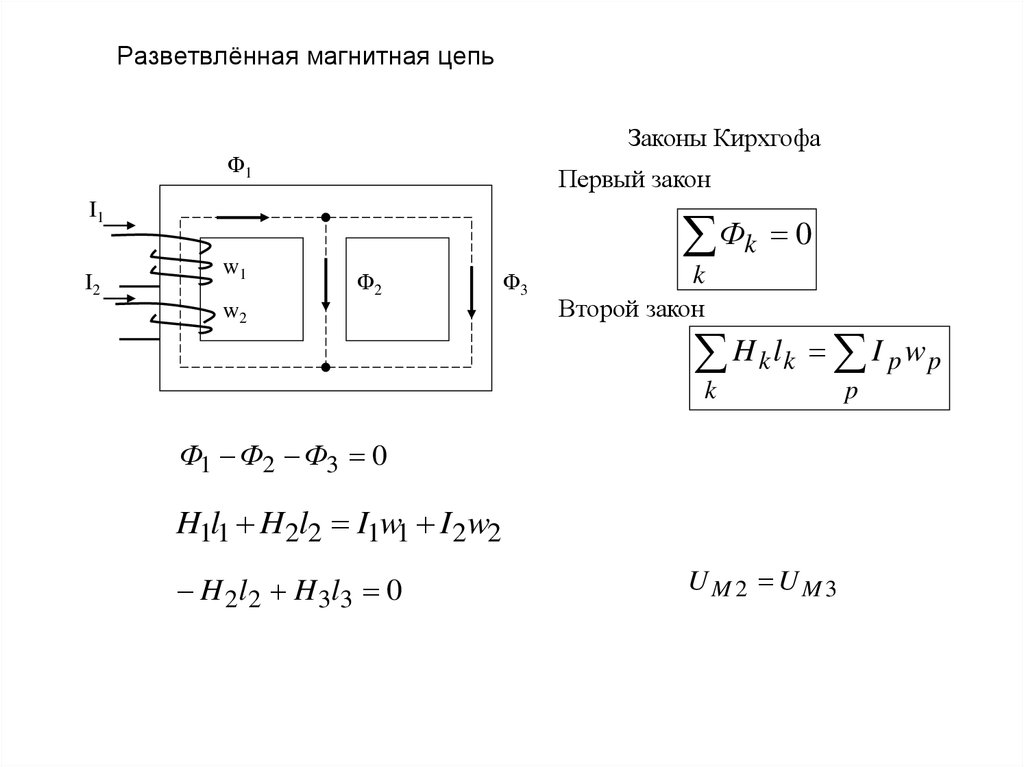
17. Разветвлённая магнитная цепь
Законы КирхгофаФ1
Первый закон
I1
I2
w1
Фk 0
Ф2
w2
Ф3
k
Второй закон
H k lk I p w p
k
Ф1 Ф2 Ф3 0
H1l1 H2l2 I1w1 I 2w2
H 2l 2 H 3l3 0
UM 2 UM3
p
18.
2. Методы анализа электрических и магнитных цепей2.1 Эквивалентные преобразования линейных электрических цепей
2.2 Метод контурных токов
2.3 Метод узловых потенциалов
2.4 Метод эквивалентного генератора
2.5 Баланс мощностей
2.6 Методы анализа нелинейных резистивных цепей постоянного тока
2.7 Методы анализа магнитных цепей с постоянными магнитными потоками
19.
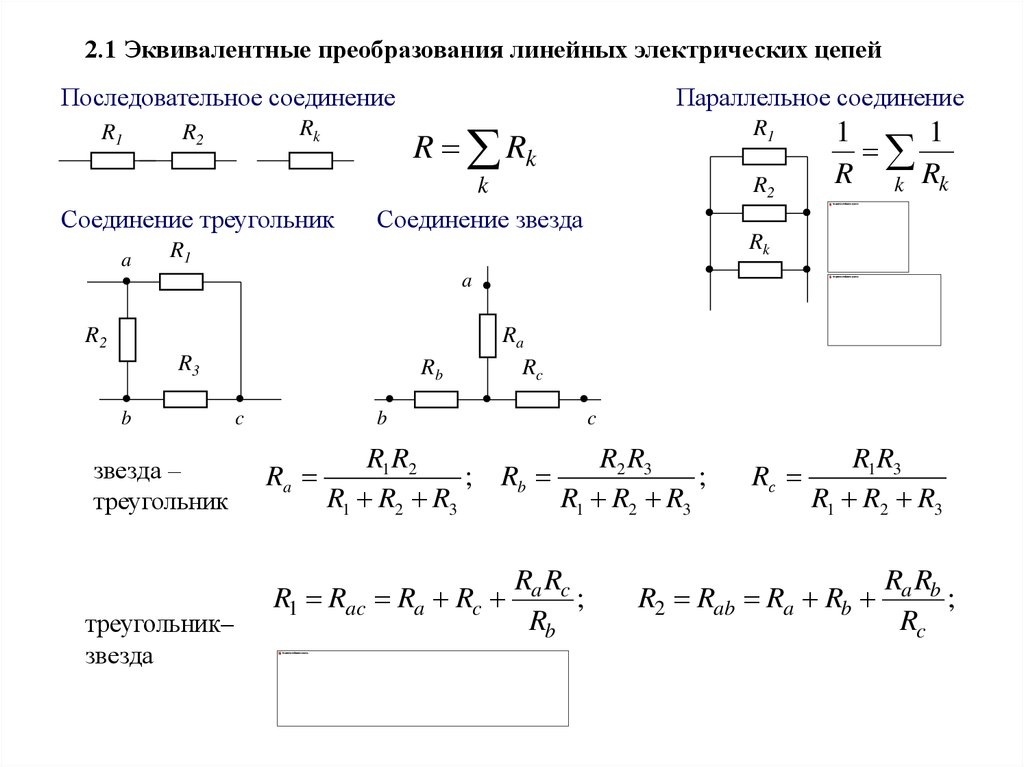
2.1 Эквивалентные преобразования линейных электрических цепейПоследовательное соединение
R1
R Rk
Rk
R2
Параллельное соединение
R1
R2
k
Соединение треугольник
a
1
1
R k Rk
Соединение звезда
Rk
R1
a
R2
R3
b
звезда –
треугольник
треугольник–
звезда
Rb
c
Ra
Rc
b
Ra
c
R2 R3
R1 R2
;
; Rb
R1 R2 R3
R1 R2 R3
R1 Rac Ra Rc
Ra Rc
;
Rb
Rс
R1 R3
R1 R2 R3
R2 Rab Ra Rb
Ra Rb
;
Rc
20.
2.2 Метод контурных токов1. Выбирают и обозначают независимые контурные токи.
Число независимых контурных токов равно
pВ q 1
Рекомендуется выбирать контурных токов так, чтобы
каждый из них проходил через один источник тока.
2. Составляют по второму закону Кирхгофа для контуров n уравнений в виде
R11 I11 R12 I 22 R1n I nn R1n 1J1 R1n pT J pT E11 ;
R I R I R I R
22 22
2 n nn
2 n 1J1 R2 n pT J pT E22 ;
21 11
Rn1I11 Rn 2 I 22 Rnn I nn Rnn 1J1 Rnn pT J pT Enn .
3. Определяют значения контурных токов.
4. Находят токи в ветвях, применяя первый закон Кирхгофа.
21.
2.3 Метод узловых потенциалов1. Один узел схемы цепи принимают базисным с нулевым потенциалом.
2. Для остальных (q - 1) узлов составляют уравнения по первому закону
Кирхгофа, выражая токи ветвей через потенциалы узлов, применяя закон
Ома.
3. Решением составленной системы уравнений определяют
потенциалы (q - 1) узлов относительно базисного.
4. Находят токи ветвей по обобщенному закону Ома.
22.
2.4 Метод эквивалентного генератораДля нахождения тока в одной ветви
1. Всю внешнюю по отношению к выделенной ветви электрическую
цепь представляют в виде некоторого эквивалентного генератора с ЭДС
ЕЭ и сопротивлением RЭ.
2. ЭДС ЕЭ определяют как разность потенциалов между точками (узлами)
электрической цепи, к которым подключена ветвь с искомым током в
режиме холостого хода.
3. Сопротивление RЭ определяют в режиме холостого хода, заменяя источники
ЭДС – нулевыми сопротивлениями, а источники тока – бесконечно большими
сопротивлениями.
4. Искомый ток в ветви определяют по закону Ома
23.
2.5 Баланс мощностейPИk PПm
k
m
PR RI 2
PE EI
PJ U J J
24.
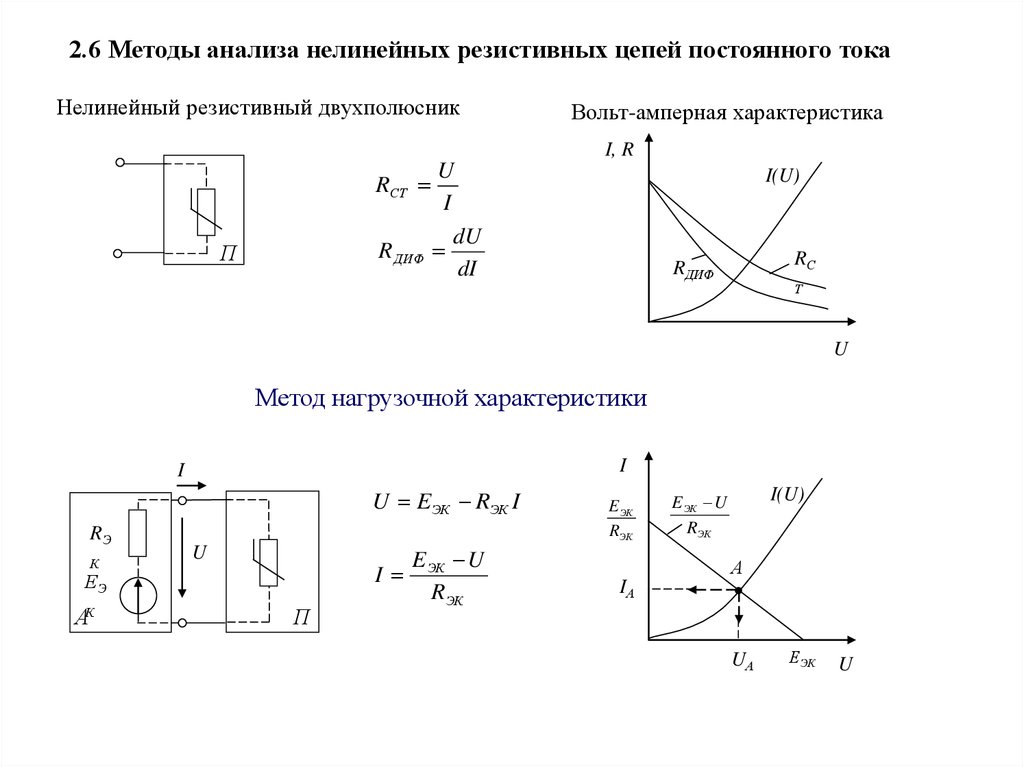
2.6 Методы анализа нелинейных резистивных цепей постоянного токаНелинейный резистивный двухполюсник
Вольт-амперная характеристика
I, R
RСТ
П
R ДИФ
U
I
dU
dI
I(U)
RС
RДИФ
Т
U
Метод нагрузочной характеристики
I
I
U EЭК RЭК I
RЭ
К
U
I
ЕЭ
АК
П
E ЭК U
RЭК
EЭК
RЭК
I(U)
EЭК U
RЭК
А
IА
UА
ЕЭК
U
25.
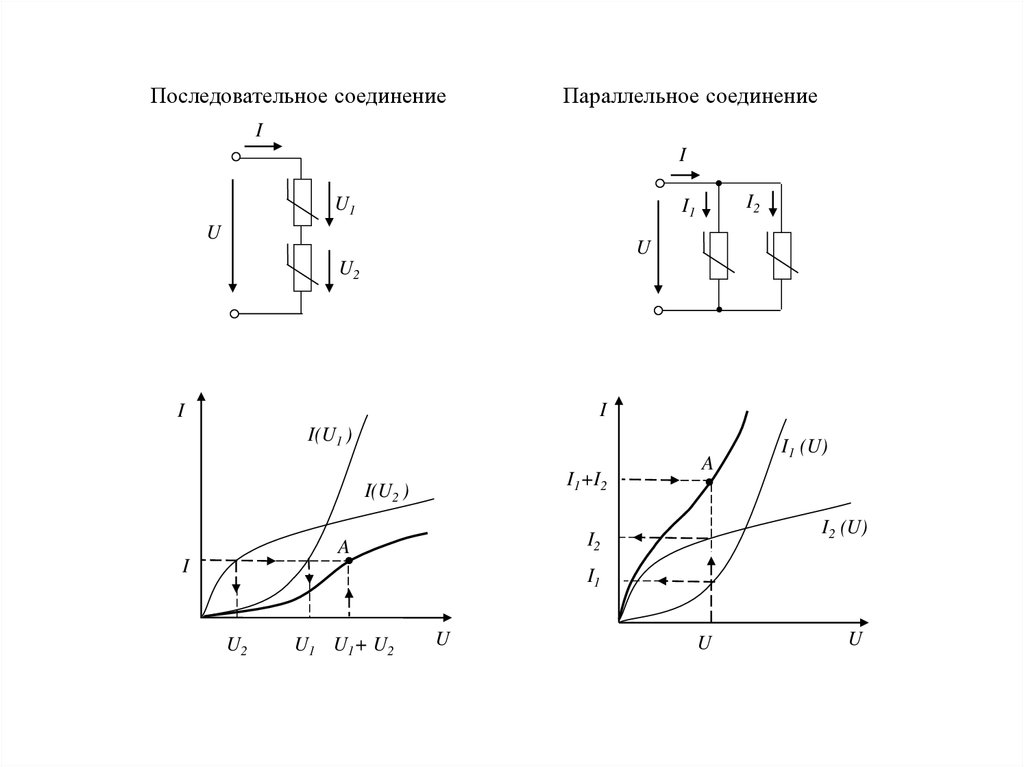
Последовательное соединениеПараллельное соединение
I
I
U1
I2
I1
U
U
U2
I
I
I(U1 )
I1+I2
I(U2 )
A
I2 (U)
I2
A
I
I1 (U)
I1
U2
U1 U1+ U2
U
U
U
26.
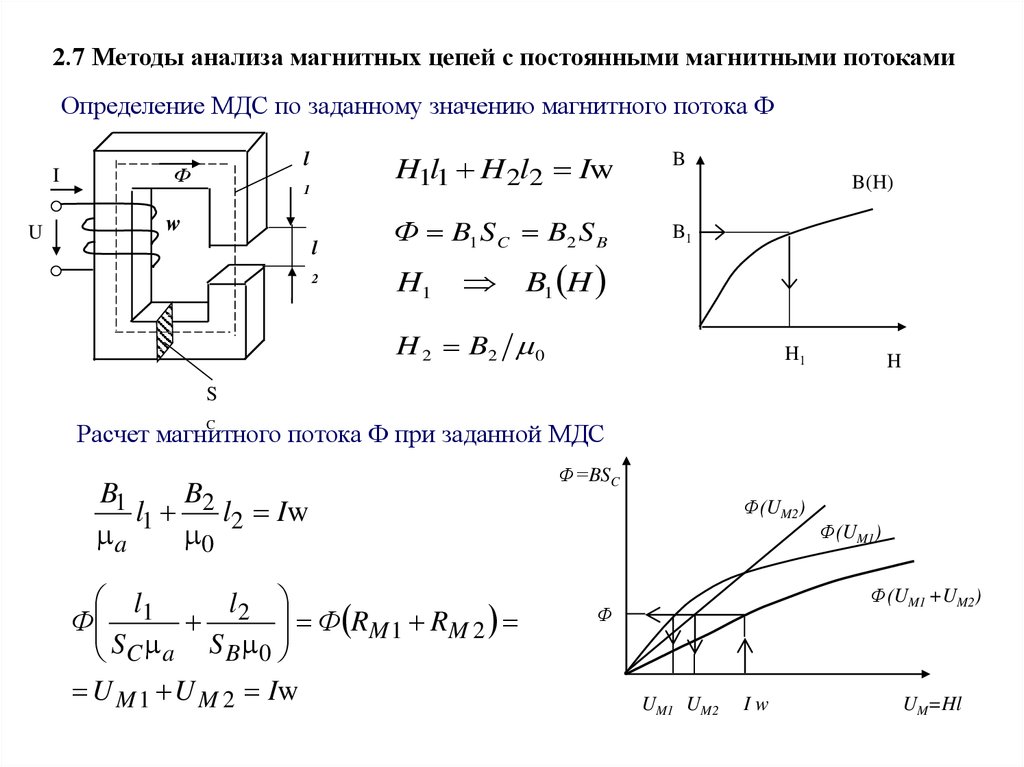
2.7 Методы анализа магнитных цепей с постоянными магнитными потокамиОпределение МДС по заданному значению магнитного потока Ф
I
U
l
Ф
1
w
l
2
H1l1 H 2l2 Iw
B
Ф B1 S C B2 S B
B1
H1
B(H)
B1 H
H 2 B2 0
H1
H
S
Расчет магнитного потока Ф при заданной МДС
C
B1
B
l1 2 l2 Iw
a
0
l
l
Ф 1 2 Ф RM 1 RM 2
SC a S B 0
U M 1 U M 2 Iw
Ф=BSC
Ф(UM2)
Ф(UM1)
Ф(UM1 +UM2)
Ф
UM1 UM2
Iw
UM=Hl
27.
3.Теория электрических и магнитных цепей переменного тока3.1 Основные понятия
3.2 Способы представления синусоидальных электрических величин
3.3 Фазовые соотношения между током и напряжением
3.4 Пассивный двухполюсник в цепи синусоидального тока
3.5 Резонансные явления в линейных электрических цепях
синусоидального тока
3.6 Мощность в цепи синусоидального тока. Баланс мощностей
3.7 Расчёт электрических цепей при периодических несинусоидальных
воздействиях
3.8 Четырёхполюсники
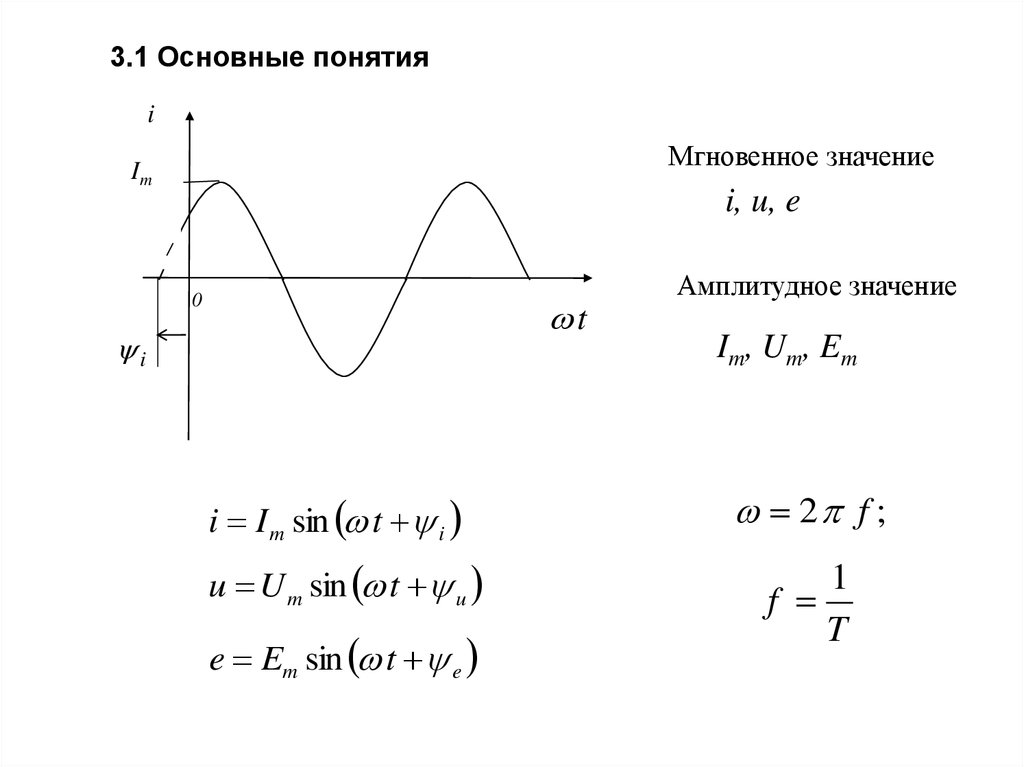
28. 3.1 Основные понятия
iМгновенное значение
Im
i, u, e
t
0
i
i I m sin t i
u U m sin t u
e Em sin t e
Амплитудное значение
Im, Um, Em
2 f ;
1
f
T
29.
Среднее значениеI СР
2
T
T 2
2
0 idt T
Действующее значение
RI T R i dt;
2
0
I
Im
2
I
m
sin t dt
0
I, U, E;
T
2
T 2
; U
T
1 2
I
i dt
T0
Um
2
; E
Em
2
2I m
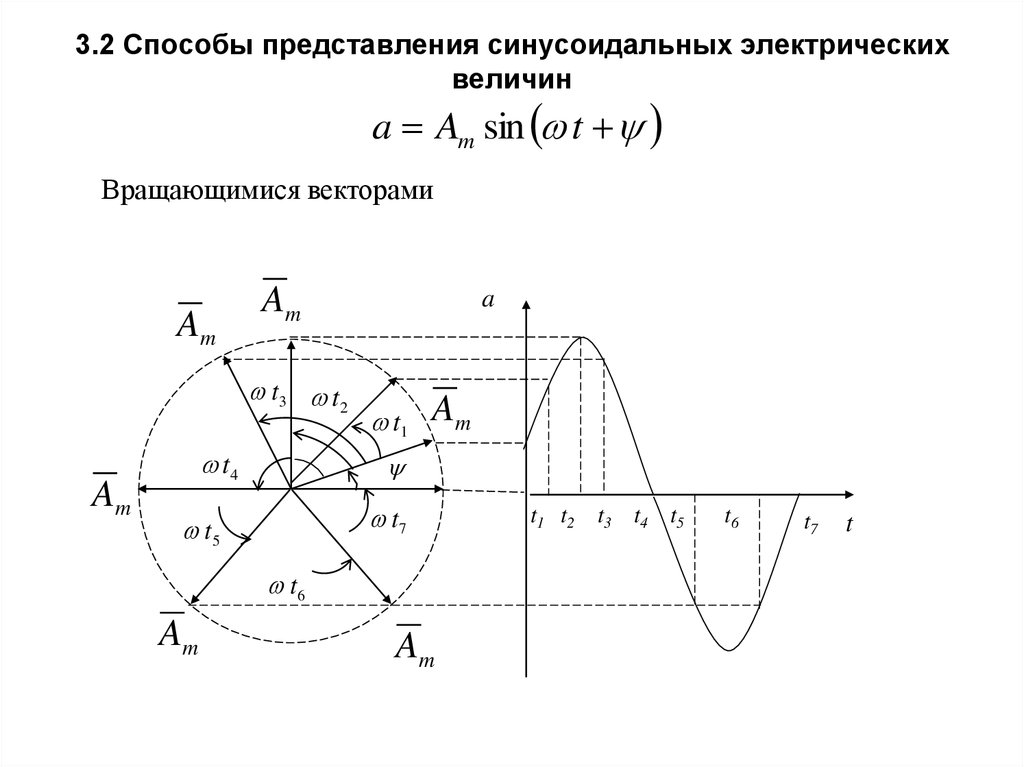
30. 3.2 Способы представления синусоидальных электрических величин
a Am sin tВращающимися векторами
Am
Am
t3 t2
Am
t4
a
t1
Am
t7
t5
t6
Am
Am
t1 t2 t3 t4 t5
t6
t7
t
31.
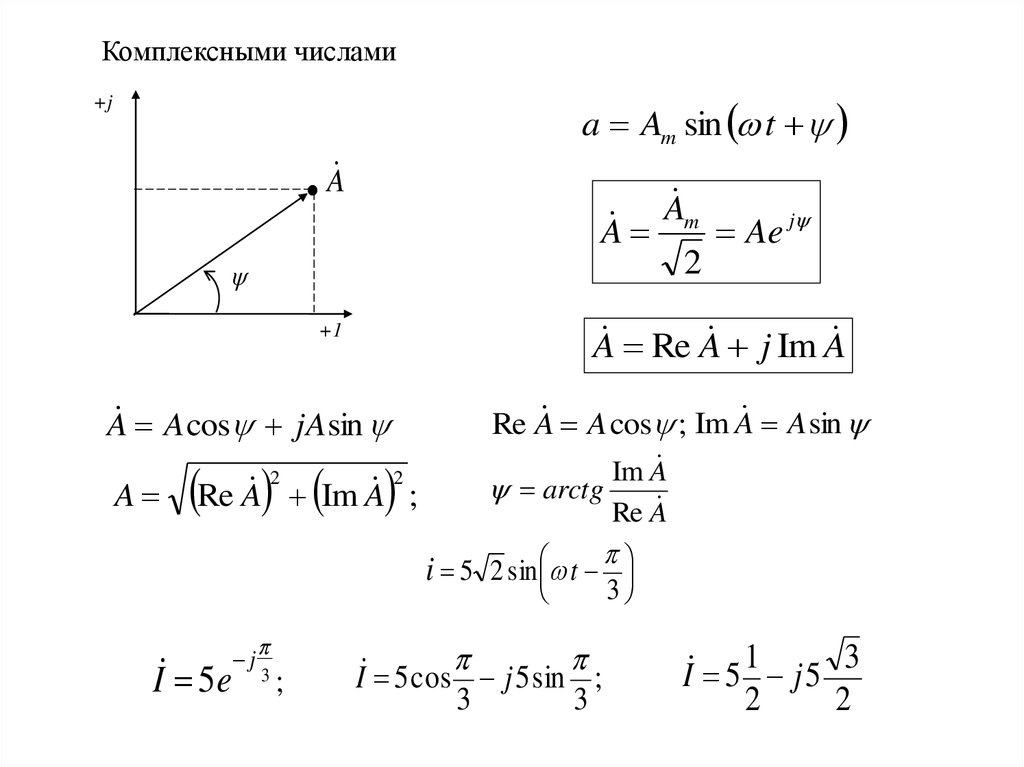
Комплексными числамиa Am sin t
+j
A
A
A m
A Re A j Im A
+1
Re A A cos ; Im A A sin
A A cos jAsin
A
Re A Im A ;
2
2
Ae j
2
Im A
arctg
Re A
i 5 2 sin t
I 5 e
j
3
;
I 5 cos j 5 sin ;
3
3
3
1
3
I 5 j 5
2
2
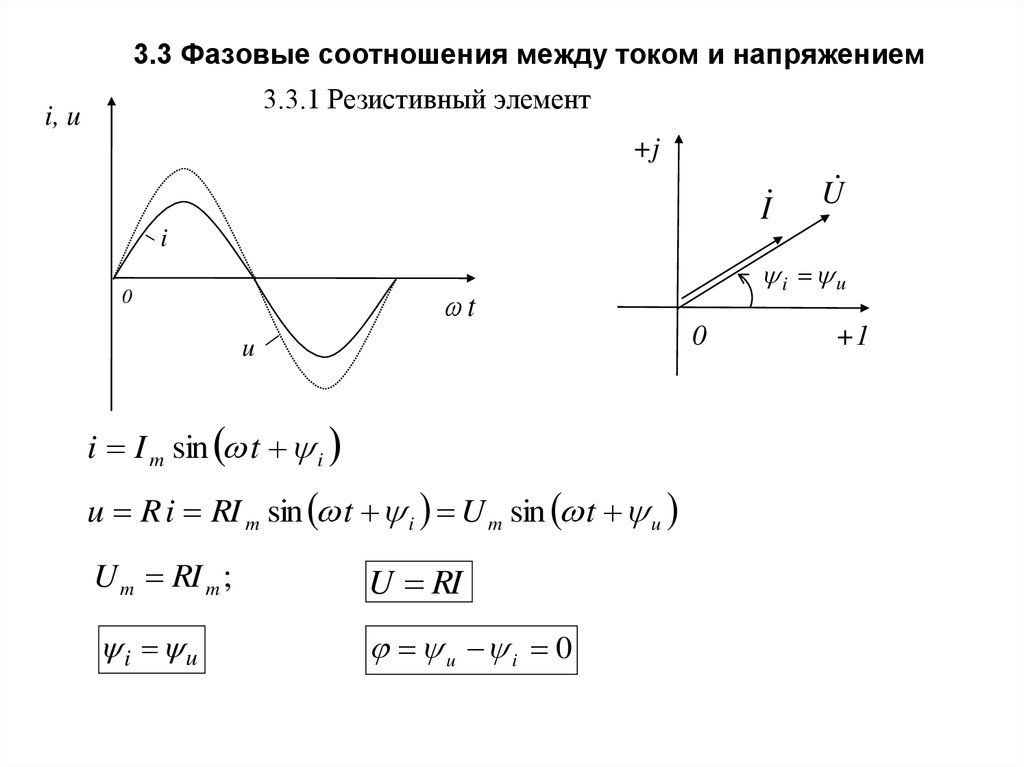
32. 3.3 Фазовые соотношения между током и напряжением
3.3.1 Резистивный элементi, u
+j
I
U
i
i u
t
0
0
u
i I m sin t i
u R i RI m sin t i U m sin t u
U m RI m ;
U RI
i u
u i 0
+1
33.
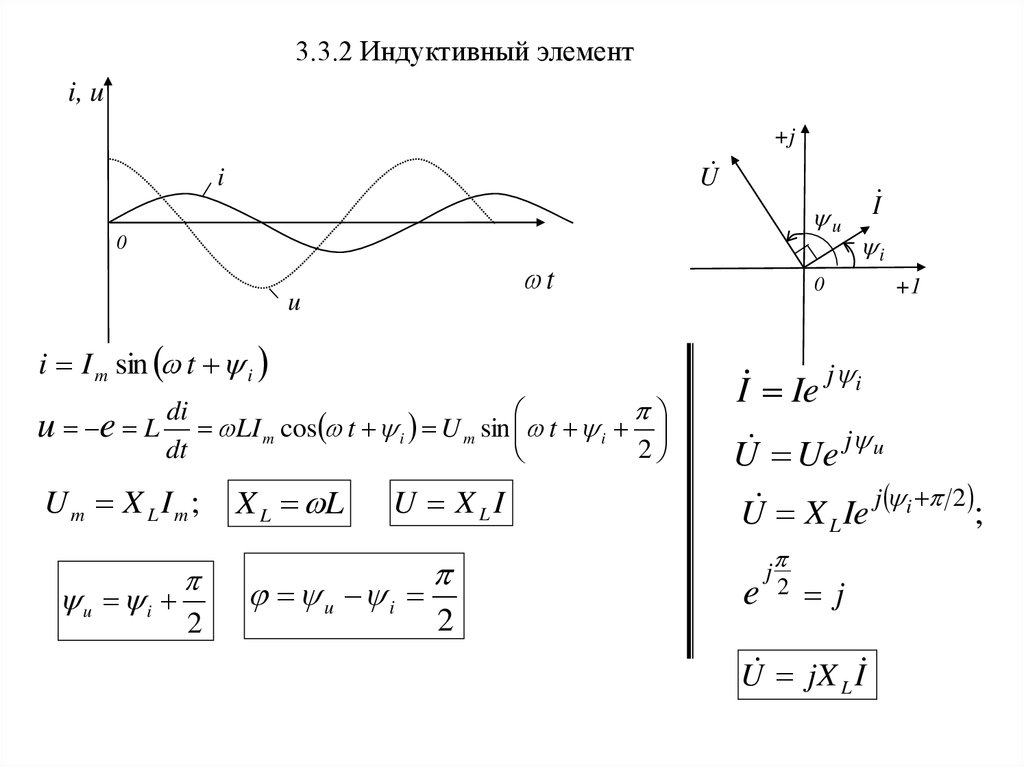
3.3.2 Индуктивный элементi, u
+j
U
i
u
0
t
u
0
i I m sin t i
u e L di LI m cos t i U m sin t i
dt
Um X L Im;
u i
2
X L L
U XLI
u i
2
I
i
2
+1
j
I Ie i
U Ue j u
j i 2
U X L Ie
;
e
j
2
j
U jX L I
34.
3.3.3 Емкостный элементi, u
+j
u
I
t
0
i
i
u
U
0
+1
u U m sin t u
i dq C du CU m cos t u I m sin t u
dt
dt
2
I m CU m ;
U XCI
1
XC
C
u i
I CU ;
1
U
I;
C
2
u i
j
I Ie i
U Ue j u
j 2
U X С Ie i
;
j
e 2
2
j
U jX С I
35. 3.4.1 Последовательное соединение участков R, L, C
3.4 Пассивный двухполюсник в цепи синусоидального тока3.4.1 Последовательное соединение участков R, L, C
I
XL
R
UR
UL
XC
Z
XL-XC
φ
UC
R
U U R U L U C RI jX L I jX C I
I
U
R j X L X C
комплексное сопротивление
Z R j X L X C ;
Z Ze
j
полное сопротивление
Z Z R2 X L X C
2
XL XC
arctg
R
Закон Ома
I U U e j u
Z Z
36. 3.4.2 Параллельное соединение участков G, L, C
I I G I L I C GU jBLU jBCUG
1
G
R
1
1
BL
X L L
BC
1
C
XC
комплексная проводимость
Y G j BL BC ;
полная проводимость
Y G 2 BL BC 2
1
Y Ye j
Z
Закон Ома
I Y U
37.
3.5 Резонансные явления в линейных электрических цепяхсинусоидального тока
3.5.1 Резонанс напряжений
X L XC
arctg
R
0
U L
U L UC
U
U
L C
I
R
Q
U C
LC
R
1
L
C
U UR
добротность колебательного контура
c p 1
UL
U
I
ωC
ωP
ωL
L p
ω
p
характеристическое сопротивление
колебательного контура
I
UC
Ip
X L XC
1
p
2Q
2
1
1 1 2Q
2
p
U
R
1
LC
38.
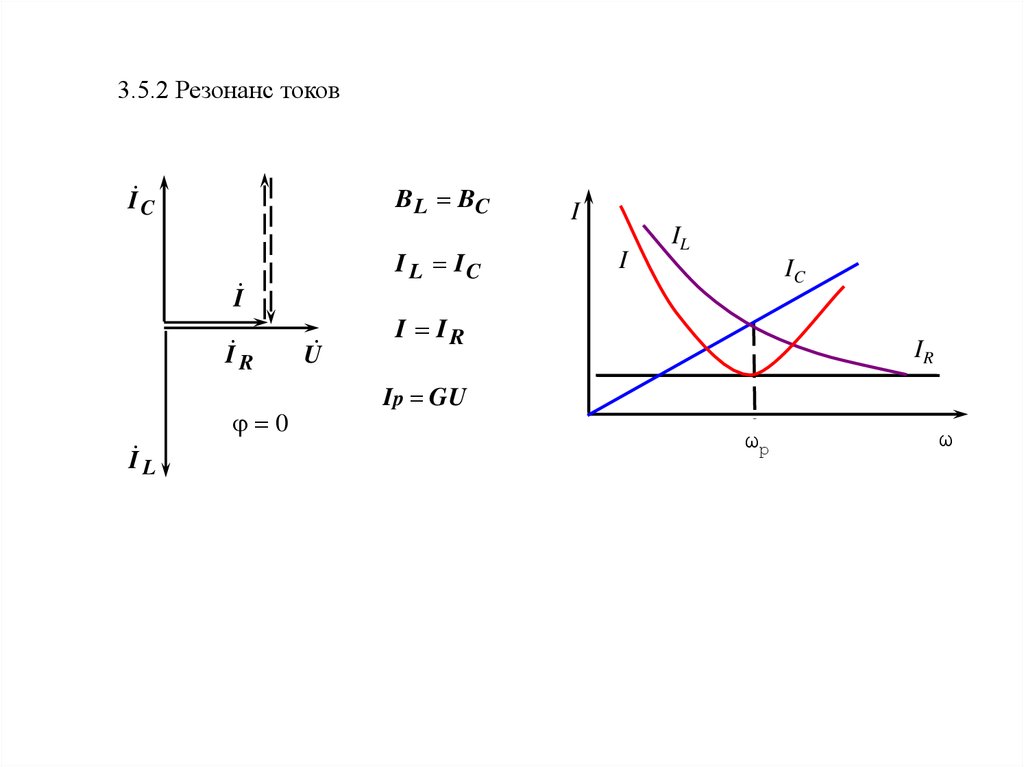
3.5.2 Резонанс токовB L BC
I C
I L IC
I
I R
0
I L
U
I
I
IL
IC
I IR
IR
Ip GU
ωp
ω
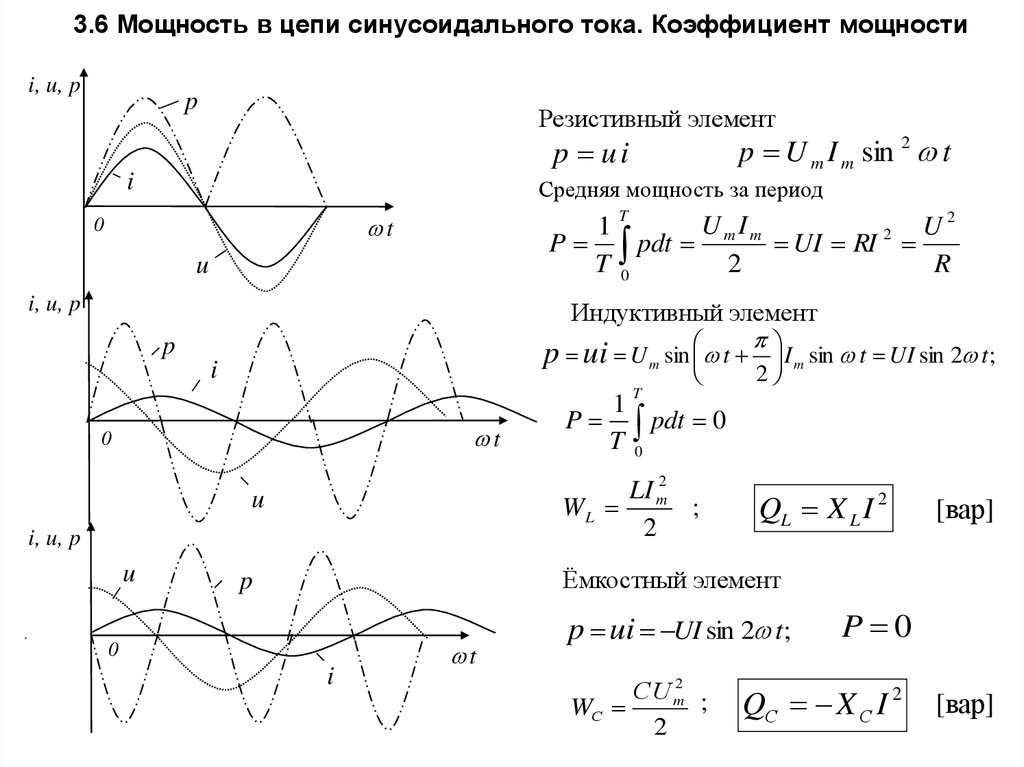
39. 3.6 Мощность в цепи синусоидального тока. Коэффициент мощности
i, u, pp
Резистивный элемент
p U m I m sin 2 t
p ui
i
Средняя мощность за период
T
UmIm
1
U2
2
P pdt
UI RI
T0
2
R
t
0
u
i, u, p
Индуктивный элемент
p ui U m sin t I m sin t UI sin 2 t;
p
i
T
t
0
i, u, p
2
1
pdt 0
T 0
LI m2
;
WL
2
u
u
P
QL X L I 2
[вар]
Ёмкостный элемент
p
0
i
t
p ui UI sin 2 t;
СU m2 ;
WС
2
P 0
QС X С I 2
[вар]
40.
u U m sin t u ;i I m sin t i ;
Активная мощность
1
p ui U m I m sin t u sin t i U m I m cos u i cos 2 t u i ;
2
T
U I
1
P pdt m m cos u i ;
P UI cos
[Вт]
T0
2
Полная мощность
Реактивная мощность
Q QL QC UI sin
[вар]
Комплексная мощность
S P jQ
S UI P 2 Q 2
S
QL - QC
φ
P
Коэффициент мощности
cos
P
S
[ВА]
41. Баланс мощности в цепи синусоидального тока
PИСТ
PR
U
ИСТ
I ИСТ cos u i RI R2
Q
ИСТ
U
ИСТ
QL QC
I ИСТ sin u i X L I L2 X C I C2
42.
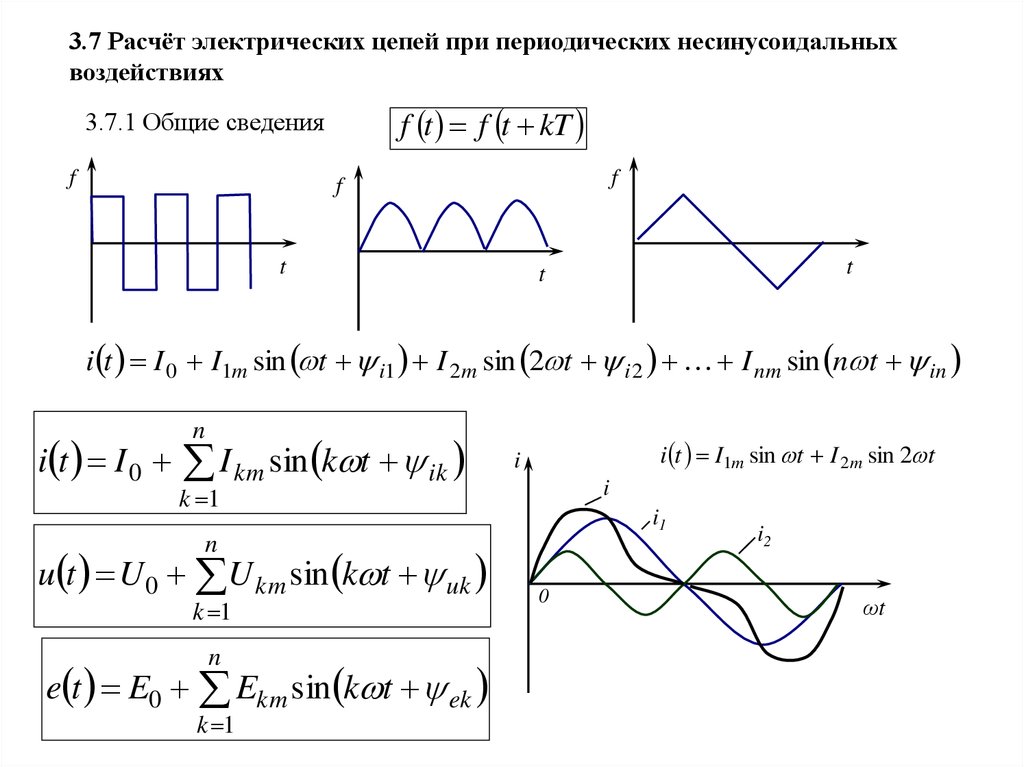
3.7 Расчёт электрических цепей при периодических несинусоидальныхвоздействиях
f t f t kT
3.7.1 Общие сведения
f
f
f
t
t
t
i t I 0 I1m sin t i1 I 2m sin 2 t i 2 I nm sin n t in
i t I 0
n
I km sin k t ik
i t I1m sin t I 2 m sin 2 t
i
i
k 1
i1
n
u t U 0 U km sin k t uk
k 1
n
e t E0 Ekm sin k t ek
k 1
0
i2
ωt
43. 3.7.2 Действующее значение периодической несинусоидальной величины
1T 2I
i dt
T0
T
i
;
0
3.
4.
T
dt i idt
;
0
2
I km
T
1.
2
1 2
2
2
I
sin
k
t
dt
I
ik
k
km
T0
2
1T
I 0 I km sin k t ik dt 0
T0
;
1T
;I dt I 2
I
0
0 0
T0
2.
;
1T
I km I lm sin k t ik sin l t il dt 0; k l
T0
I
I 02
n
k 1
I k2
U
U 02
n
U k2
k 1
44. 3.7.3 Коэффициенты, характеризующие несинусоидальные величины
Коэффициент формыkф
I
I ср
Коэффициент амплитуды
ka
Im
I
Коэффициент пульсаций
kп
I1m
I0
Коэффициент гармоник
, I ср
1T
i t dt
T0
Iг
k г , I г I 22 I 32 I 42
I
45. 3.7.4 Мощность периодического несинусоидального тока
p u i1.
1T
P u idt ;
T0
;
1T
U km sin k t uk I km sin k t ik dt U k I k cos k , k uk ik ;
T0
2.
1T
U 0 I 0 dt U 0 I 0
T0
3.
1T
1T
U 0 I km sin k t ik dt 0;
I 0U km sin k t uk dt 0 ;
T0
T0
4.
1T
U km sin k t uk I lm sin l t il dt 0; k l ;
T0
P U0I0
n
;
U k I k cos k
k 1
Q
n
U k I k sin k
k 1
46.
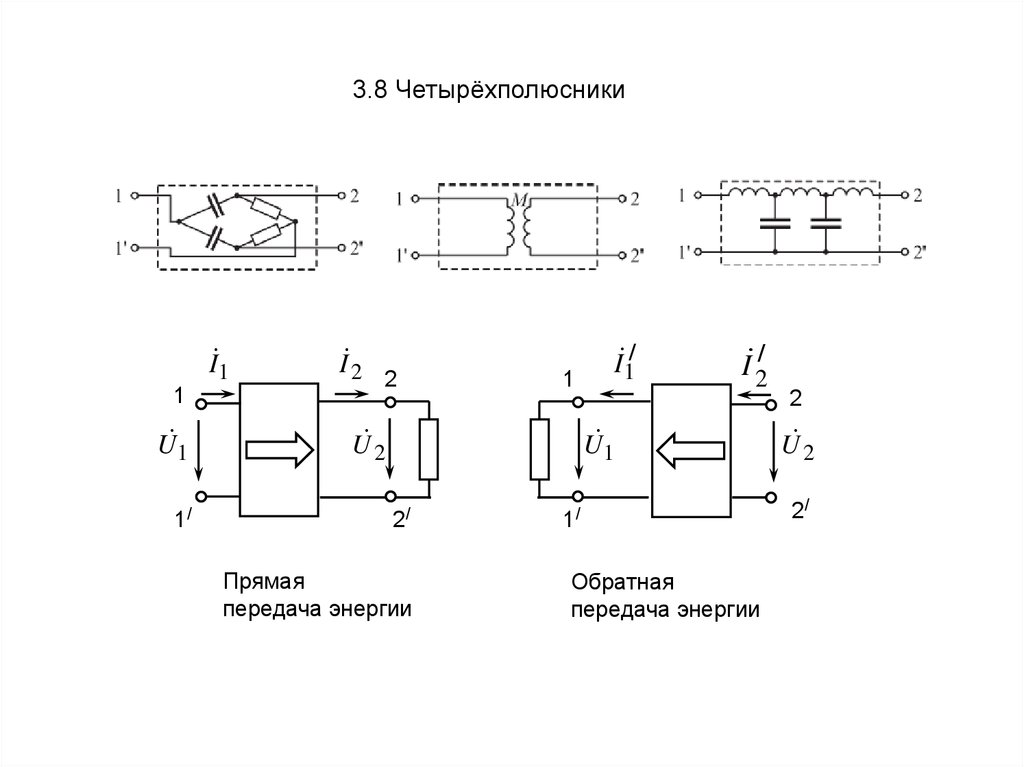
3.8 ЧетырёхполюсникиI 1
1
U 1
1/
I 2
2
I 1/
1
U 2
I 2/
U 1
2/
Прямая
передача энергии
1/
Обратная
передача энергии
2
U 2
2/
47.
Системы уравнений пассивных четырёхполюсниковФорма А
Форма В
Форма Y
U 1
U 2
A
I1
I2
U 1 A11U 2 A12 I 2
I A U A I
U 2
U 1
/ B /
I 2
I1
U 2 B11U 1 B12 I 1/
I / B U B I /
I 1
U 1
/ Y
I 2
U 2
I 1 Y 11U 1 Y 12U 2
I / Y U Y U
1
2
2
21 2
21 1
21 1
22 2
22 1
22
2
48.
Системы уравнений пассивных четырёхполюсниковФорма Z
Форма H
Форма F
I 1
U 1
Z /
I 2
U 2
U 1
I 1
/ H
I 2
U 2
U 1
I 1
F /
U 2
I 2
U 1 Z 11 I 1 Z 12 I 2/
U Z I Z I /
2
21 1
22 2
U 1 H 11 I 1 H 12U 2
I / H I H U
2
21 1
22
2
I 1 F 11U 1 F 12 I 2/
U 2 F 21U 1 F 22 I 2/
49.
Связь между коэффициентами четырёхполюсникаA11 A22 A12 A21 1
Y 21 Y 12
B11 B 22 B12 B 21 1
Z 21 Z 12
H 21 H 12
Для симметричного четырёхполюсника
A11 A 22
B11 B 22
Y 11 Y 22
Z 11 Z 22
H 11 H 22
F 11 F 22
F 21 F 12
50.
Уравнения четырёхполюсника с А-параметрамиПрямое включение
U 1 AU 2 B I 2
I C U D I
1
2
U 1
A
U 2 I 0
2
I 1
D
I 2 U 0
2
U 1
B
I 2 U 0
2
I 1
C
U 2 I 0
2
2
AD BC 1
Обратное включение
U 1 D U 2 B I 2
I C U A I
1
2
2
для симметричного четырёхполюсника
A D
51.
Определение параметров четырёхполюсникаПрямое включение
U 1x AU 2 x
I C U
1x
2x
U 1k B I 2k
I D I
1k
U 1x A
Z 1x
C
I 1x
U 1k
B
Z 1k
D
I 1k
2k
Обратное включение
Z 2x
D
C
Z 2k
B
A
52.
Схемы замещения четырёхполюсникаТ-образная
Z1
П-образная
Z/1
Z2
2
1
1
Z/2
Z3
1/
2/
AT 1
CT
Z1
Z3
1
Z3
A 1
Z1
C
BT Z 1 Z 2
DT 1
Z2
2
2/
1/
Z1Z 2
Z3
/
AП 1
Z2
Z3
D 1
C
Z/3
Z1
BП Z1
/
/
Z3
/
1
1
Z
CП / / / 1 /
Z2 Z3 Z2Z3
Z3
1
C
Z1 B
/
Z2
/
B
A 1
/
Z
D 1 1/
Z2
Z3
/
B
D 1
53.
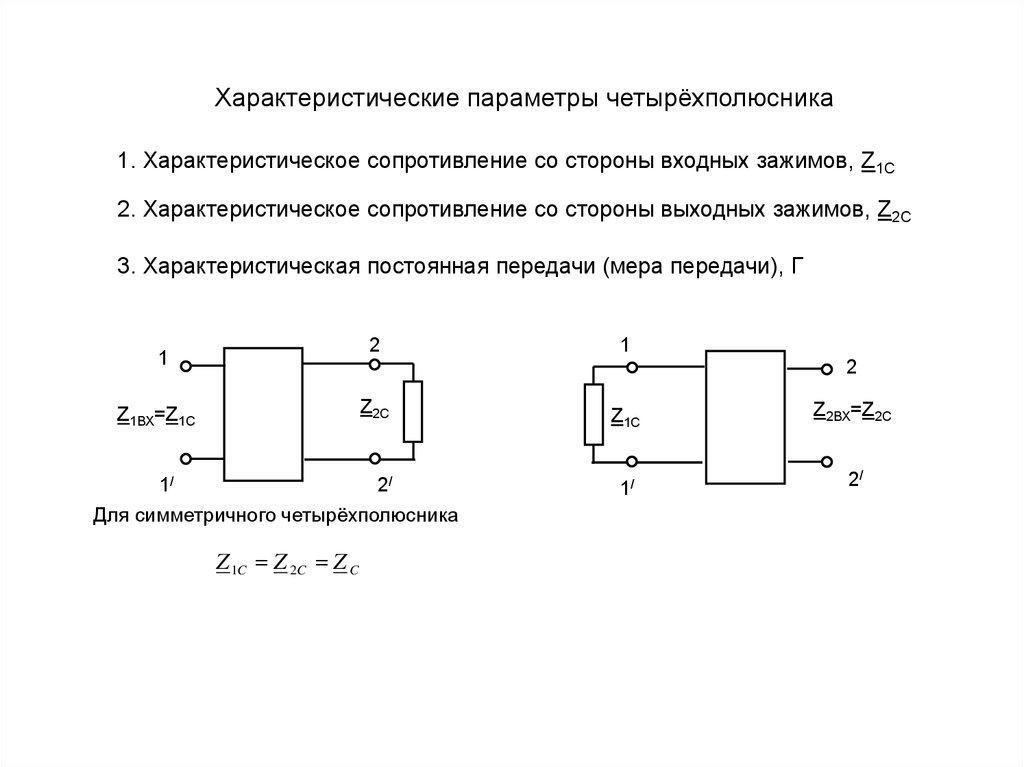
Характеристические параметры четырёхполюсника1. Характеристическое сопротивление со стороны входных зажимов, Z1C
2. Характеристическое сопротивление со стороны выходных зажимов, Z2C
3. Характеристическая постоянная передачи (мера передачи), Г
2
1
1
2
Z2C
Z1ВХ=Z1C
1/
2/
Для симметричного четырёхполюсника
Z 1C Z 2C Z C
Z1C
Z2ВХ=Z2C
1/
2/
54.
Постоянная передачиj
1 U 1 I 1
ln
2 U 2 I 2
Для симметричного четырёхполюсника
U 1 U 2
ZC
I
I
1
2
U 1 I 1
e e e j
U 2 I 2
U
U 1
U
ln
ln 1 e j 1 2 ln 1 j 1 2 j
U2
U 2
U 2
коэффициент затухания (ослабления) напряжения
ln
U1
,
U2
дБ 10 lg
Нп
коэффициент фазы
1 2 ,
рад
U1 I1
P
10 lg 1
U2I2
P2
дБ 20 lg
U1
U2
55.
Определение характеристических параметровчерез А-параметры уравнений четырёхполюсника
Z 1C
AB
CD
Z 2C
DB
CA
ln
AD BC
Для симметричного четырёхполюсника
ZC
B
C
ln A BC
через сопротивления холостого хода и короткого замыкания
Z1C Z1X Z1K
th
sh
ch
BC
AD
Z 2C Z 2 X Z 2 K
Z 1K
Z 1X
Z 2K
Z 2X
1 1 th
ln
2 1 th
56.
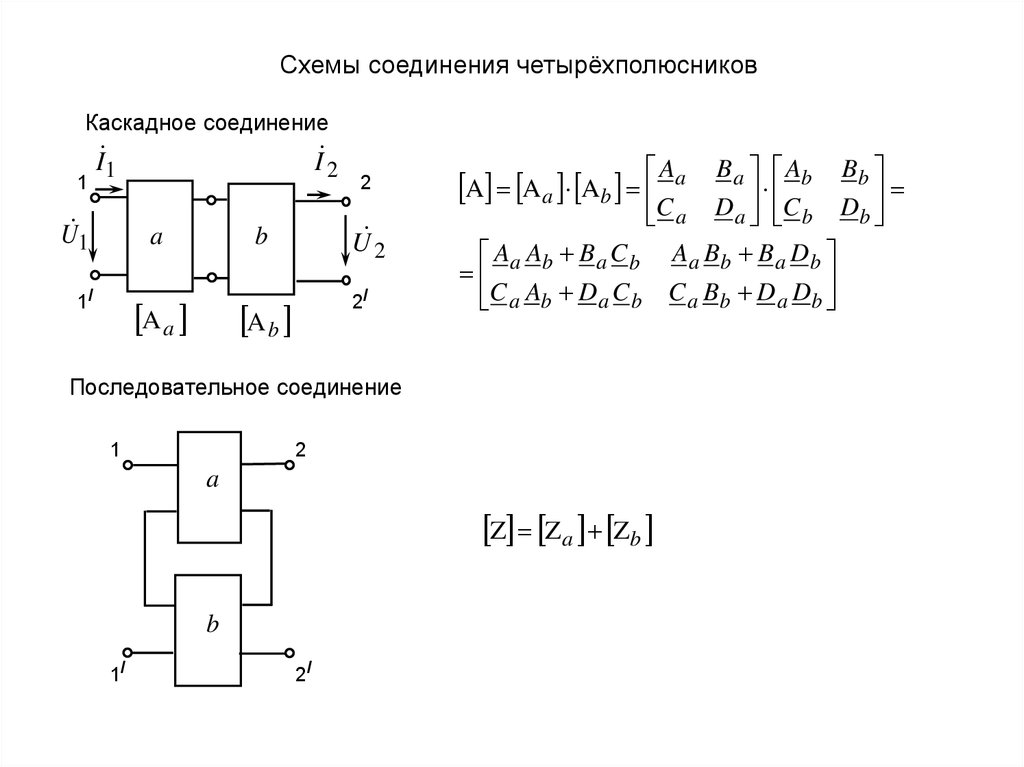
Схемы соединения четырёхполюсниковКаскадное соединение
1
I 2
I 1
U 1
a
1/
U 2
b
A a
2
2/
A b
Aa
C a
A A a Ab
A A Ba Cb
a b
C a Ab D a C b
Последовательное соединение
1
2
a
Z Za Zb
b
1/
2/
B a Ab B b
D a C b D b
Aa B b B a D b
C a B b D a D b
57.
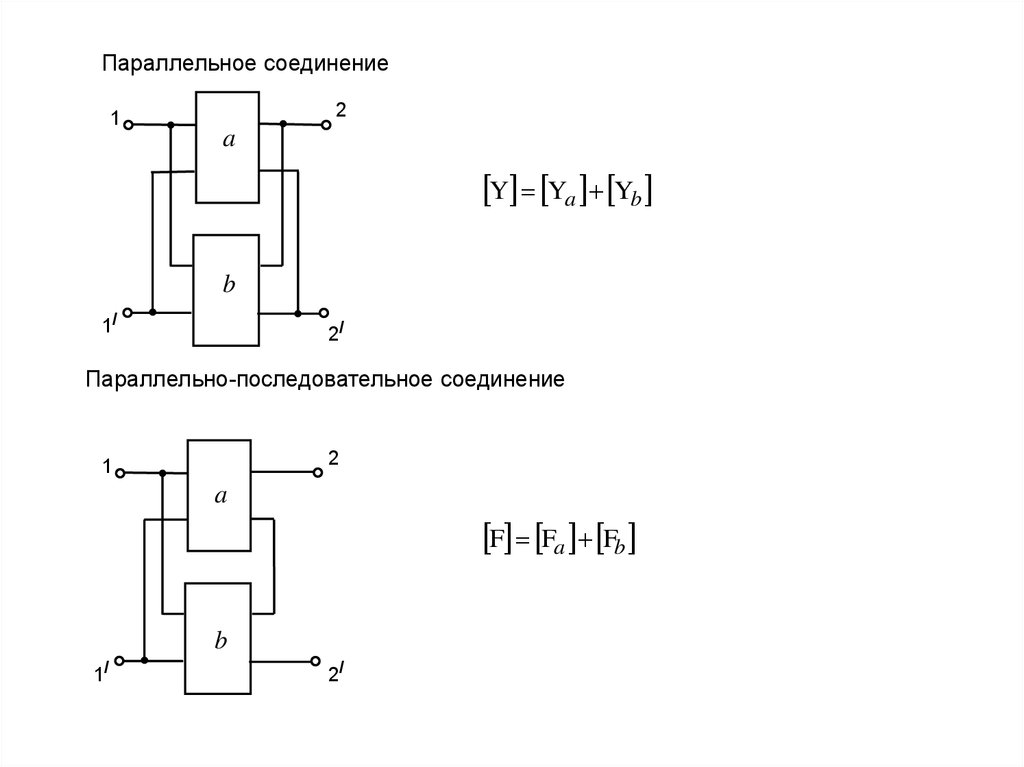
Параллельное соединение2
1
a
Y Ya Yb
b
1/
2/
Параллельно-последовательное соединение
2
1
a
F Fa Fb
b
1/
2/
58.
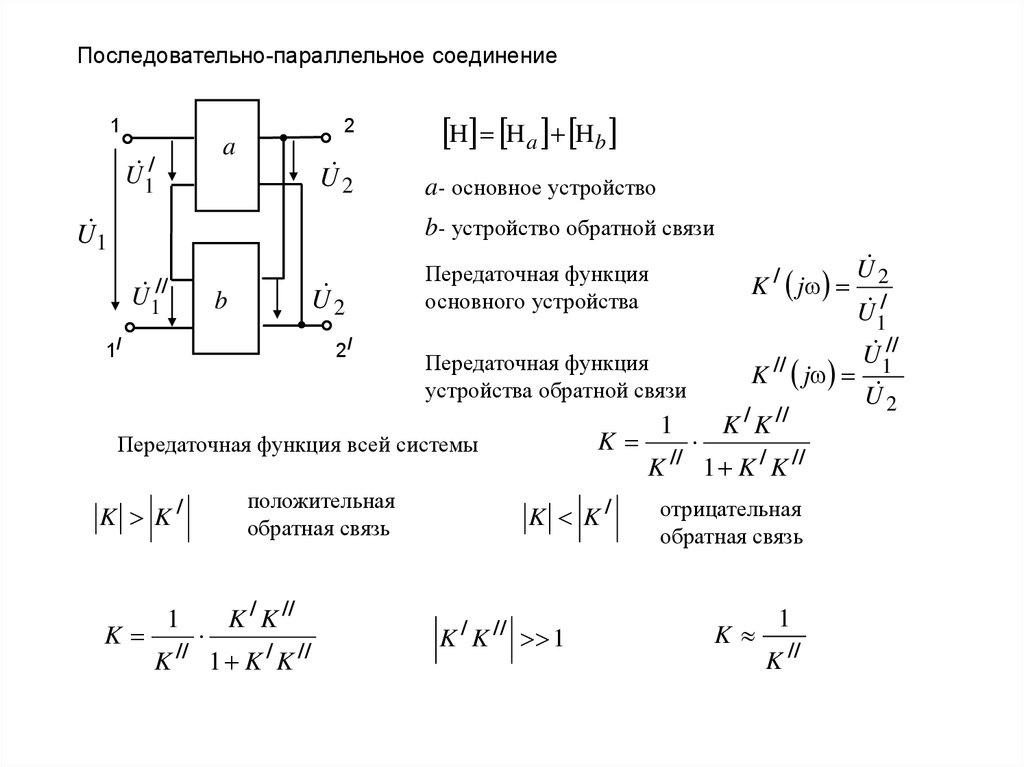
Последовательно-параллельное соединение1
2
a
U 1/
U 2
U 1
H Ha Hb
a- основное устройство
b- устройство обратной связи
U 1//
U 2
b
1/
2/
U 2
K j
U /
Передаточная функция
основного устройства
/
K
Передаточная функция всей системы
1
K
положительная
обратная связь
K K/
K
1
K / K //
K // 1 K / K //
K // j
Передаточная функция
устройства обратной связи
K K/
K / K // 1
//
K / K //
1 K / K //
отрицательная
обратная связь
K
1
K //
1
U 1//
U 2
59. 4. Переходные процессы в линейных электрических цепях
4.1 Начальные условия и законы коммутации4.2 Классический метод расчёта переходных процессов
4.2.1 Общие положения
4.2.2 Переходные процессы в RL и RC-цепях
4.2.3 Переходные процессы в цепях с двумя накопителями энергии
60. 4.1 Начальные условия и законы коммутации
i пр – ток установившегося режимаt – момент коммутации
u пр – напряжение установившегося режима
t + – начальный момент времени
i св – ток свободного процесса
u св – напряжение свободного процесса
i = i пр + i св
u = u пр + u св
после коммутации
t - – момент времени,
непосредственно
предшествовавший коммутации
Законы коммутации
Для индуктивного элемента
Для емкостного элемента
uC t uC t
iL t iL t
WM L i L2 t 2 i L2 t1
;
t
2
t 2 t1
iL t , uC t
t t 2 t1 0 и iL t1 iL t 2 ;
- начальные условия
iL t 0 iL 0 ,
uC t 0 uC 0
WM
t
61.
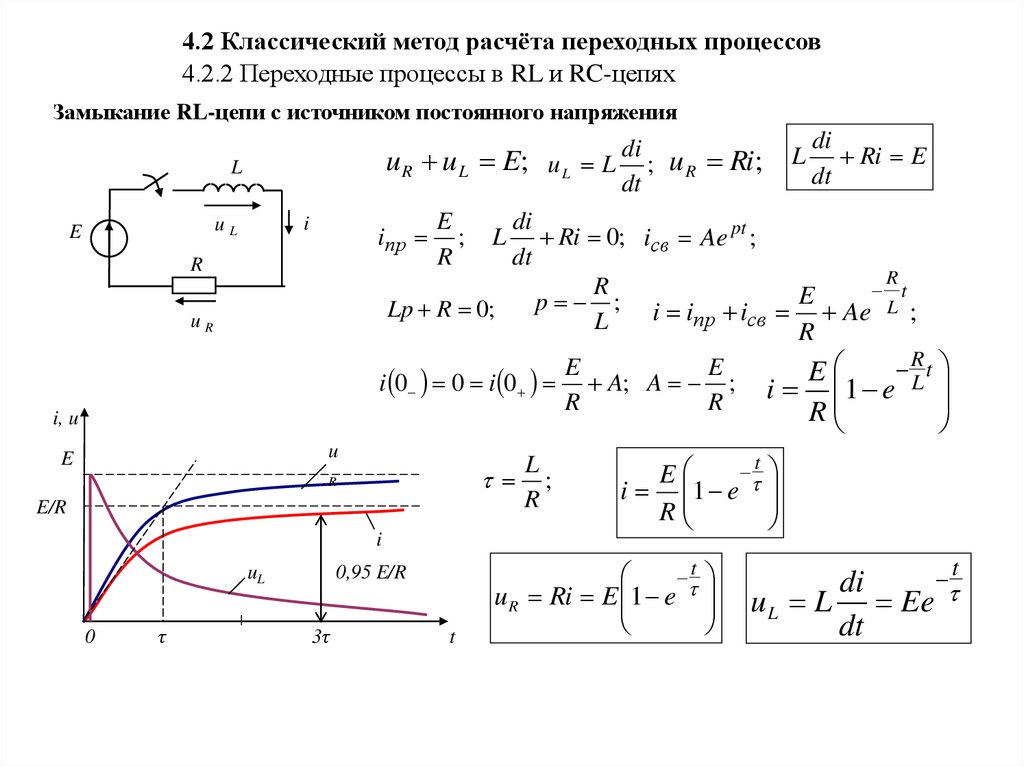
4.2 Классический метод расчёта переходных процессов4.2.2 Переходные процессы в RL и RC-цепях
Замыкание RL-цепи с источником постоянного напряжения
u R u L E; u L L di ; u R Ri;
dt
L
E
;
R
di
Ri E
dt
di
Ri 0; iсв Ae pt ;
dt
R
R
t
E
p ; i i i Ae L ;
Lp R 0;
пр св
L
R
E
E
Rt
E
i 0 0 i 0 A; A ; i 1 e L
R
R
R
i
uL
E
L
iпр
R
uR
L
i, u
u
E
R
E/R
i
uL
0
τ
0,95 E/R
3τ
t
L
;
R
E
i 1 e
R
t
u R Ri E 1 e
t
t
di
u L L Ee
dt
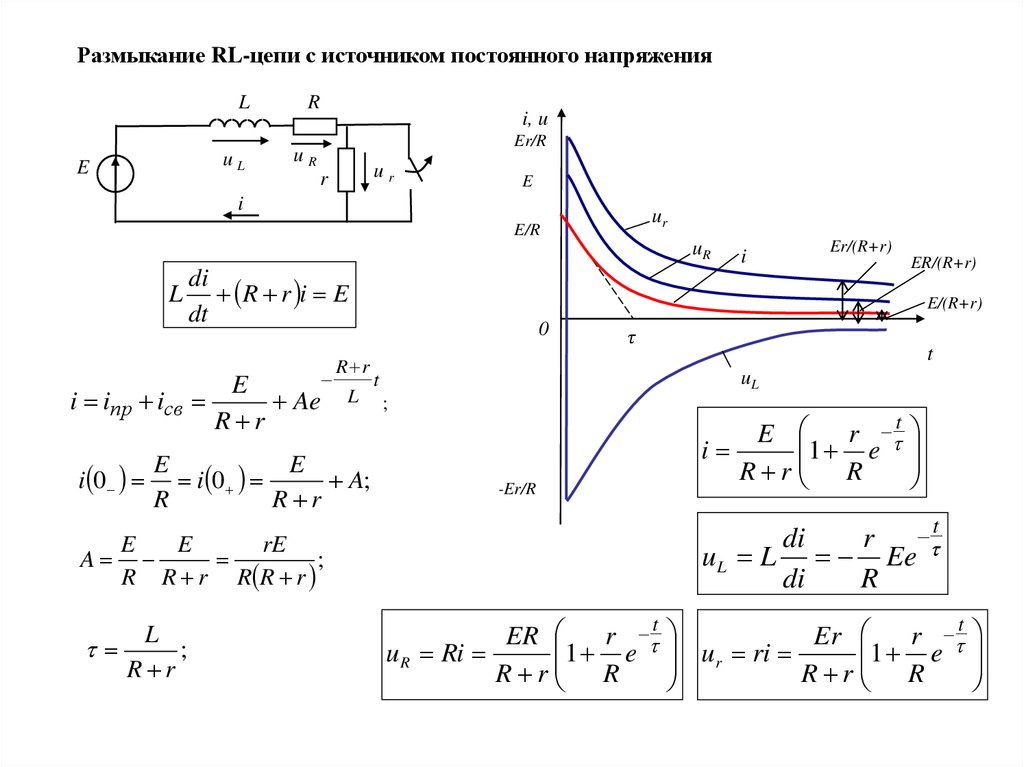
62.
Размыкание RL-цепи с источником постоянного напряженияL
uL
E
R
i, u
Er/R
uR
ur
r
E
i
ur
E/R
uR
di
L R r i E
dt
E
i iпр iсв
Ae
R r
i 0
R r
L
E
E
i 0
A;
R
R r
Er/(R+r)
ER/(R+r)
E/(R+r)
0
τ
t
uL
t
;
t
E
r
1 e
i
R r R
-Er/R
t
di
r
u L L Ee
di
R
E
E
rE
A
;
R R r R R r
L
;
R r
i
ER
r
u R Ri
1 e
R r R
t
t
Er
r
ur ri
1 e
R r R
63.
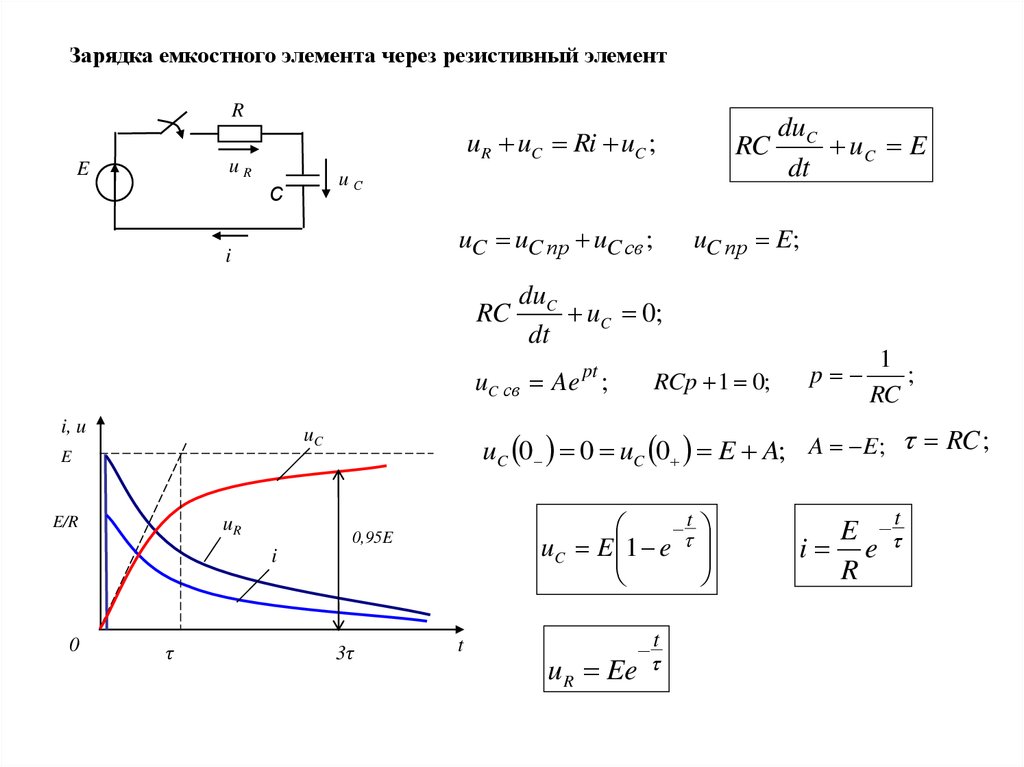
Зарядка емкостного элемента через резистивный элементR
uR
E
RC
uC uC пр uC св ;
uC пр E;
uС
С
i
RC
duC
uC 0;
dt
uC св Ae ;
pt
i, u
E
uR
t
uC E 1 e
0,95E
i
0
τ
RCp 1 0;
p
1
;
RC
uC 0 0 uC 0 E A; A E; RC ;
uC
E/R
du C
uC E
dt
uR uC Ri uC ;
3τ
t
u R Ee
t
t
E
i e
R
64.
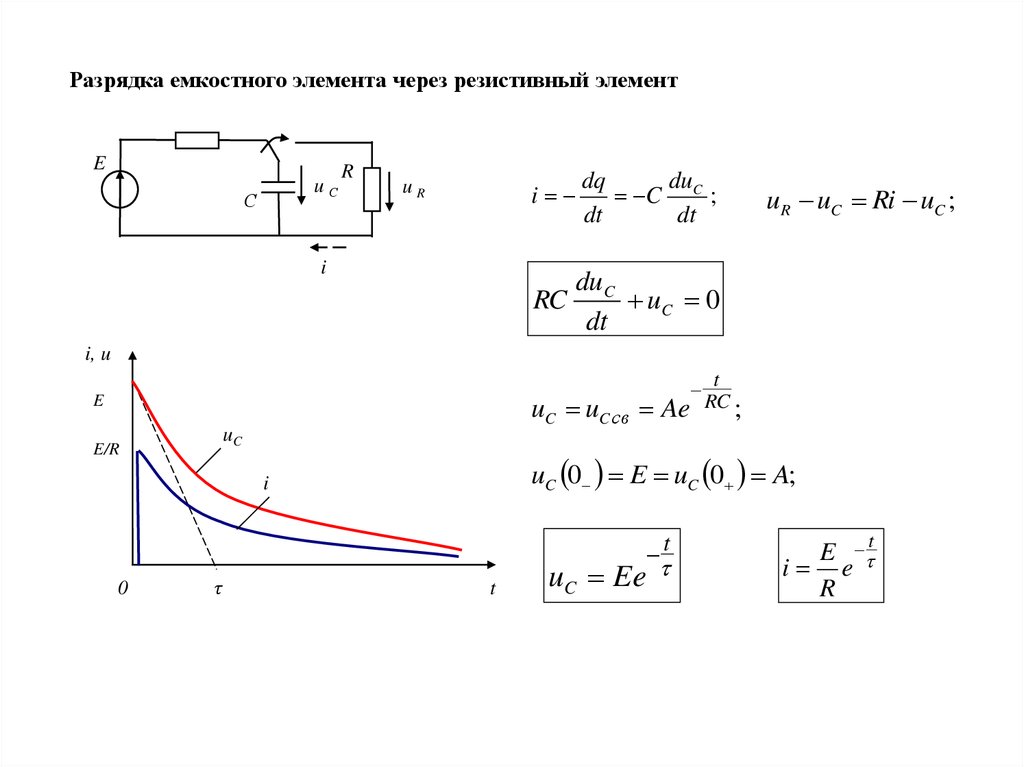
Разрядка емкостного элемента через резистивный элементE
uС
С
R
uR
i
i
RC
du
dq
C C ;
dt
dt
uR uC Ri uC ;
du C
uC 0
dt
i, u
uC uC св
E
uC
E/R
uC 0 E uC 0 A;
i
0
τ
t
Ae RC ;
t
uC Ee
t
t
E
i e
R
65. 4.2.3 Анализ переходных процессов в цепях с двумя накопителями энергии
Ru L u R u C E;
i
d 2 uC
di
u L L LC
;
dt
dt 2
uR
L
E
С
uL
uС
LCp RCp 1 0;
i C
p1, 2
duC
;
dt
d 2 uC
du C
LC
RC
uC E
2
dt
dt
uC uC у uC св ;
2
u R Ri RC
uC у E ;
R
R2
1
;
2
2L
4 L LC
duC
pt
pt
Cp1 A1e 1 Cp2 A2 e 2
dt
uC 0 0 uC 0 E A1 A2 ,
i 0 0 i 0 Cp1 A1 Cp2 A2
A1
uC св A1e
uC E A1e
p2 E
;
p1 p2
A2
p1t
p1t
A2e
A2e
p2t
p1 E
p 2 p1
R2
1
4 L2 LC
- апериодический процесс
R2
1
4 L2 LC
- колебательный процесс
p2t
;
66. Анализ переходных процессов в цепях с двумя накопителями энергии
Колебательный процессp1, 2 j 0
R
2L
0
- коэффициент затухания
1
LC 2
- собственная угловая частота колебательного процесса
E j 0
A1
;
2 j 0
uC E
i
A2
E j 0
2 j 0
E
t
e sin 0t
0 LC
E t
e sin 0t
0 L
tg
0




































 Физика
Физика








