Электрические цепи синусоидального тока. Основные понятия

1.

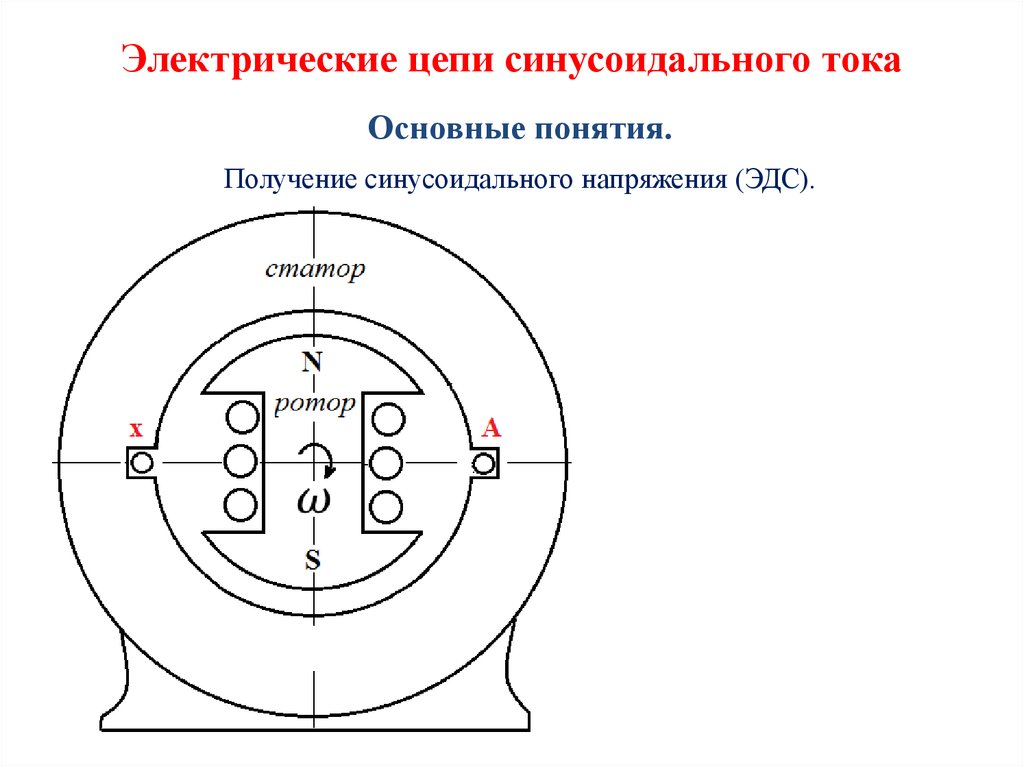
Электрические цепи синусоидального тока
Основные понятия.
Получение синусоидального напряжения (ЭДС).

2.

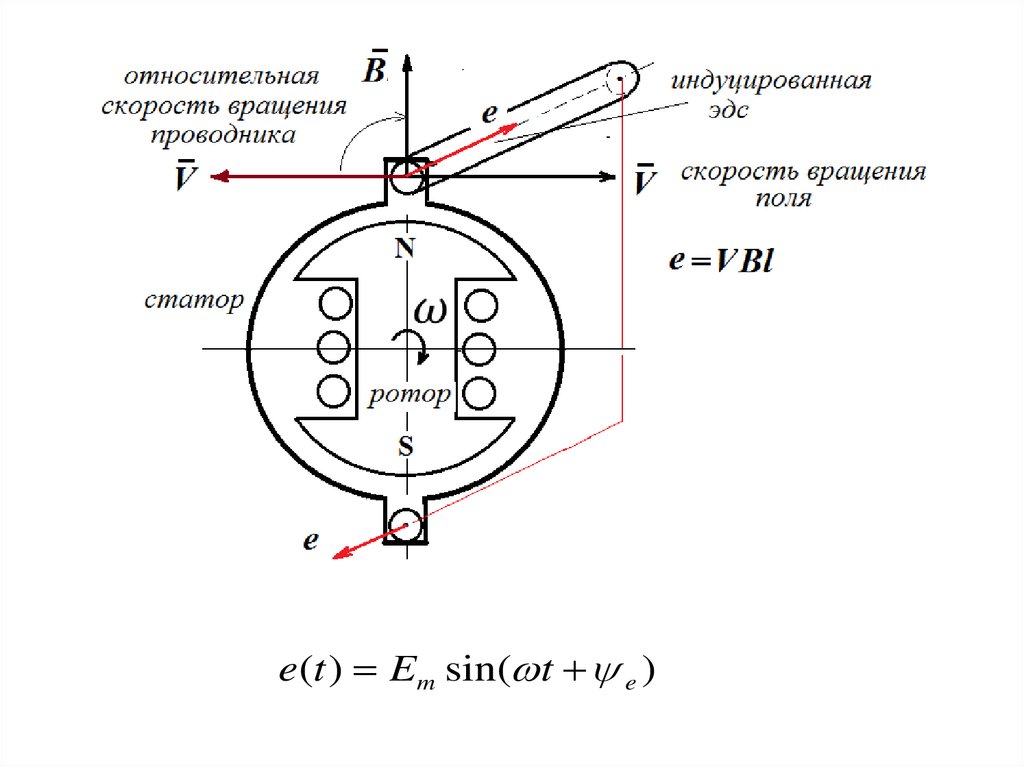
e(t ) Em sin( t e )

3.

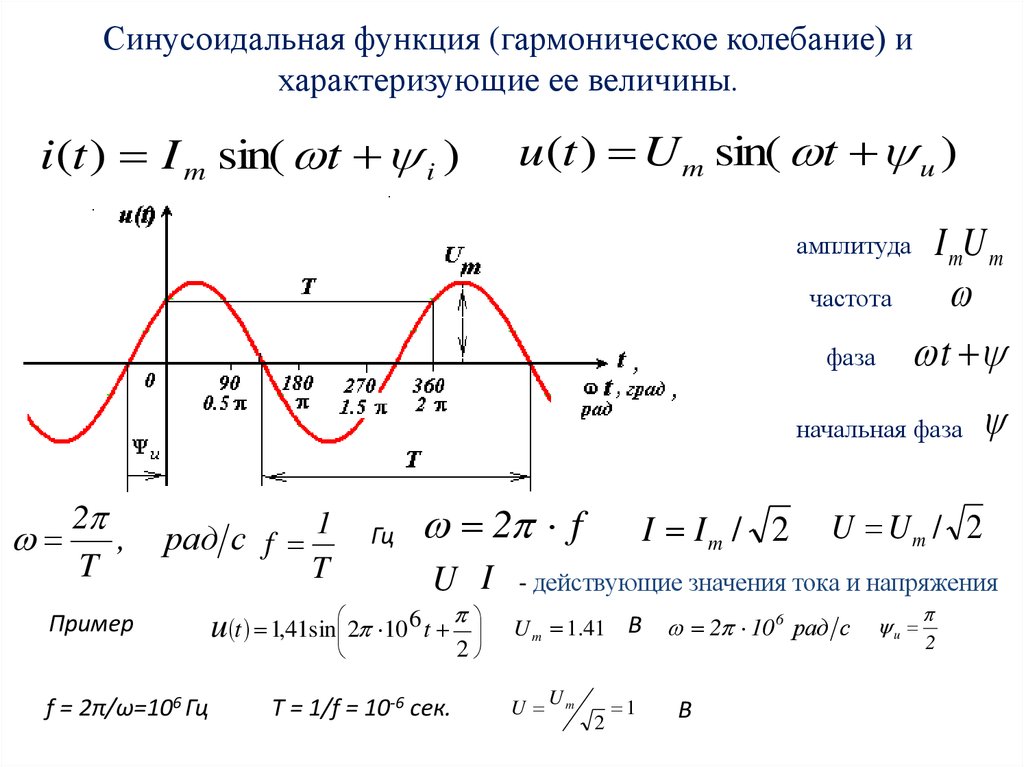
Синусоидальная функция (гармоническое колебание) и
характеризующие ее величины.
i(t ) I m sin( t i )
u (t ) U m sin( t u )
амплитуда
частота
фаза
I mU m
t
начальная фаза
2
,
T
рад с f 1
Пример
f = 2π/ω=106 Гц
Гц
T
2 f
U I
u t 1,41sin 2 10 6 t
Т = 1/f = 10-6 сек.
2
I Im / 2
U Um / 2
- действующие значения тока и напряжения
U m 1.41 B
U
Um
2
1
2 10 6 рад с
B
u
2

4.

Представление гармонических колебаний комплексными числами
u (t ) U m sin( t u ) Im(U m e j ( t u ) ) Im(U m cos( t u ) jU m sin( t u ))
U m U me
I m I m e j i
j u
комплексная амплитуда напряжения
комплексная амплитуда тока
U m sin( t u ) U m e j u
Комплекс действующего значения напряжения и тока
U Ue
j u
I Ie j i
изображение на комплексной плоскости по координатам в полярной системе
координат
j 1

5.

Комплексы в декартовой системе координат
U a jb
b U sin u
a U cos u
U a b
2
2
b
u arctg
a

6.

Синусоидальный ток в элементах
R
L
C
в режиме воздействия на них гармонического колебания
электрическое сопротивление
R
i(t ) I m sin( t i )
I Ie j i
u(t ) i(t ) R I m R sin( t i )
U R I
u i
U R I
u i 0
Комплексное сопротивление для электрического сопротивления
U
Zr R
I
R
Комплексная проводимость
1
1
Yr
G
Zr R

7.

временная и векторная диаграммы тока и напряжения на элементе
.
индуктивность
R
L
i(t ) I m sin( t i )
di(t )
u (t ) L
I m L cos( t i ) I m L sin( t i 900 )
dt

8.

j ( 1 900 )
U m I m Le
j LI m
X L L
j ( 1 900 )
U I Le
j LI
индуктивное сопротивление синусоидальному току
Z L jX L
комплексное сопротивление индуктивности
1
YL
j bL
ZL
1
1
bL
X L L
комплексная проводимость индуктивности
проводимость индуктивности
u i 90 0

9.

частотная характеристика индуктивного элемента
временная и векторная диаграммы тока и напряжения на индуктивности

10.

емкость
C
i(t ) I m sin( t i )
1
1
1
u (t ) i (t )dt
I m ( cos( t i ))
I m sin( t i 90 0 )
C
C
C
1
1
1
j ( i 900 )
j i
U
I e
j
I e
I
C
C
j C
1
XС
C
Z С jX C
емкостное сопротивление синусоидальному току
комплексное сопротивление емкости

11.

1
YС
j bC
ZС
1
bC
C
XC
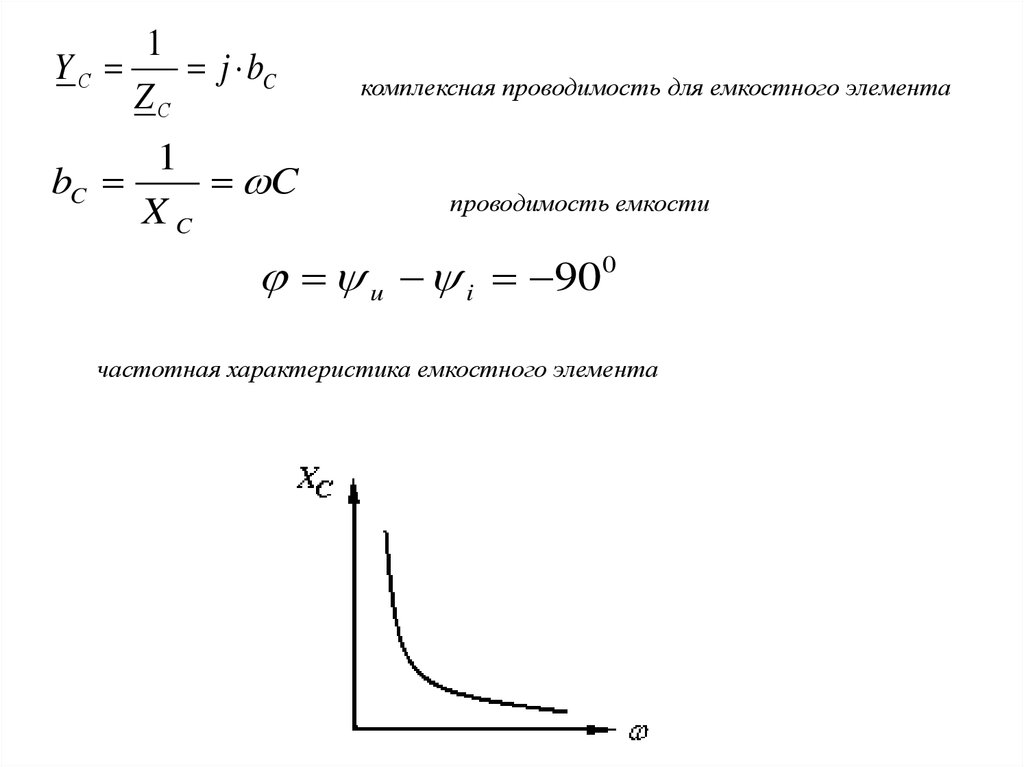
комплексная проводимость для емкостного элемента
проводимость емкости
u i 90
0
частотная характеристика емкостного элемента

12.

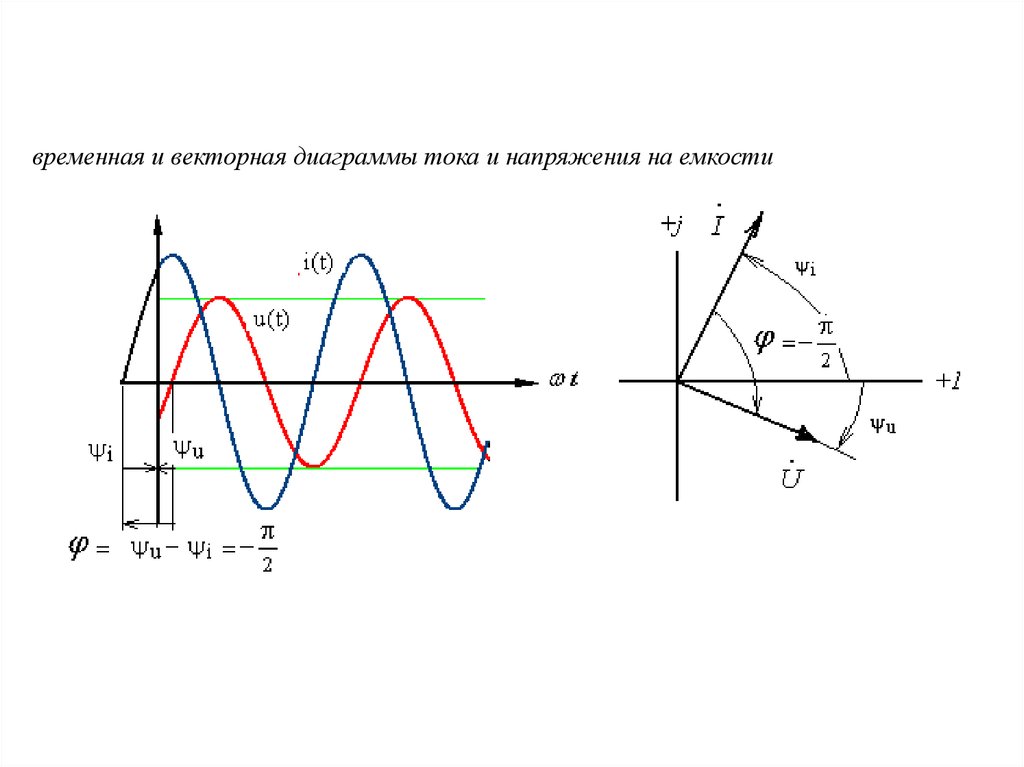
временная и векторная диаграммы тока и напряжения на емкости

13.

Законы Ома и Кирхгофа в комплексной форме
первый закон Кирхгофа в комплексной форме
n
0
I
k
k 1
второй закон Кирхгофа в комплексной форме
n
U
k
k 1
n
E
k
k 1
закон Ома в комплексной форме
U I Z

14.

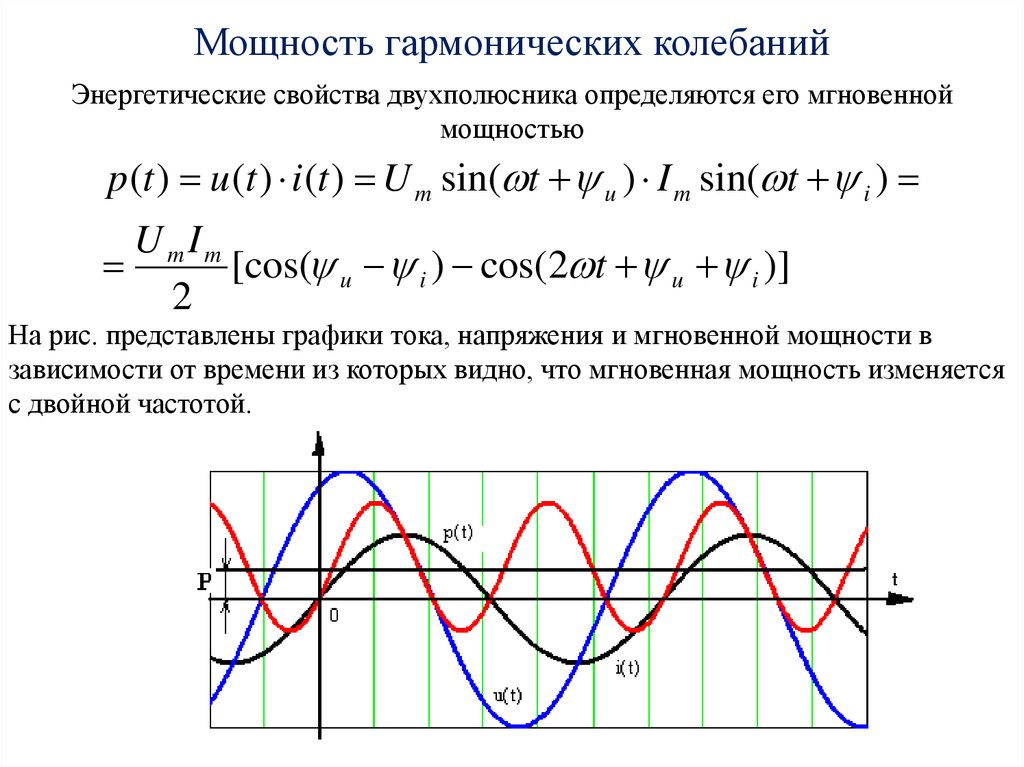
Мощность гармонических колебаний
Энергетические свойства двухполюсника определяются его мгновенной
мощностью
p (t ) u (t ) i (t ) U m sin( t u ) I m sin( t i )
UmIm
[cos( u i ) cos(2 t u i )]
2
На рис. представлены графики тока, напряжения и мгновенной мощности в
зависимости от времени из которых видно, что мгновенная мощность изменяется
с двойной частотой.

15.

Мгновенная мощность , как видно из графика и аналитического выражения
имеет постоянную составляющую.
. Это
средняя мощность, потребляемая двухполюсником за период колебания .
1
P
T
T
1
0 p(t )dt 2 U m I m cos U I cos
Физический смысл средней мощности заключается в том, что она показывает
мощность безвозвратно потребляемую цепью. Эта мощность выделяется в
цепи либо в виде тепловой энергии (нагревание резисторов), либо
преобразуется в другие виды энергии (механическая работа, например, в
электродвигателях , химическая энергия , например при зарядке
аккумуляторов, электромагнитное излучение, например, как в
радиопередатчиках и радиоприемниках).
Средняя за период мощность называется активная мощность цепи ,
измеряется в ваттах (Вт)
Рассмотрим возможность определения активной мощности по заданным
комплексным значениям напряжения и тока.

16.

Введем понятие комплексная мощность цепи.
где
I
1
S U m I m U I
2
сопряженный комплекс действующего значения тока.
1
S U m e j u I m e j i UIe j ( u i ) UIe j UI cos jUI sin
2
Вещественная часть полученного комплексного числа есть активная мощность
цепи
P Re( S ) U I cos
Мнимая часть комплексной мощности называется реактивная мощность цепи
Q Im( S ) U I sin

17.

Физический смысл реактивной мощности – она оценивает максимальную
скорость обмена энергией между источником и приемником. Реактивная
мощность связана с энергиями электрического поля в емкостях схемы и
магнитного поля в индуктивностях . Реактивная мощность измеряется в вольтамперах реактивных( Вар).
Модуль комплексной мощности называется полная мощность цепи
S S UI
Таким образом можно записать:
P S cos
Q S sin
S P Q
2
2
Как видно из полученных формул реактивная мощность – это алгебраическое
число. Ее знак зависит от знака угла сдвига фаз между током и напряжением
u i

18.

, то есть от характера реактивного сопротивления цепи , при
0
,что соответствует индуктивному сопротивлению реактивная мощность
положительна, при
0
,что соответствует емкостному сопротивлению реактивная мощность
отрицательна.
Понятие комплексная мощность оказывается удобным при расчете
установившихся гармонических колебаний. Пусть двухполюсник имеет
комплексное сопротивление
Z r jx
По определению комплексной мощности имеем:
S U I I Z I I I (r jx) I 2 r jI 2 x
Следовательно,
P I r
2
Q I 2x
Косинус угла сдвига фаз между напряжением и током называется
коэффициентом мощности.
P
P
cos
S
P Q
2
2

19.

Этот коэффициент характеризует степень использования полной мощности
Чем больше
cos
при заданной средней мощности, тем меньше потери в установках,
передающих энергию
Проблема повышения
cos
является одной из важнейших проблем энергетики .

20.

Расчет простейших электрических цепей в режиме
гармонических колебаний
дано
R
L
e(t ) Em sin( t e )
решение
E E e j e
E
I
Z0
Zr R
Z0 Zr ZL
ZL j XL
U r I Z r
XL L
U L I Z L
комплексная схема замещения

21.

расчет ЭЦ при числовых значениях
Em 100 2
В
E
E m 100
2
R
100 Ом
L
0.318 Гн
f 50 Гц
j150
E 100e
2 f 2 50 314
X L L 314 0.318 100
Z L j X L j100
1/сек
частота
Ом
Ом
j 150
E
100
e
j 300
I
1 e
R Z L 100 j100
j 300
j 600
U L I Z L 1 e
j100 100 e
j 300
j 300
U r I R 1 e
100 100 e
e 15 0

22.

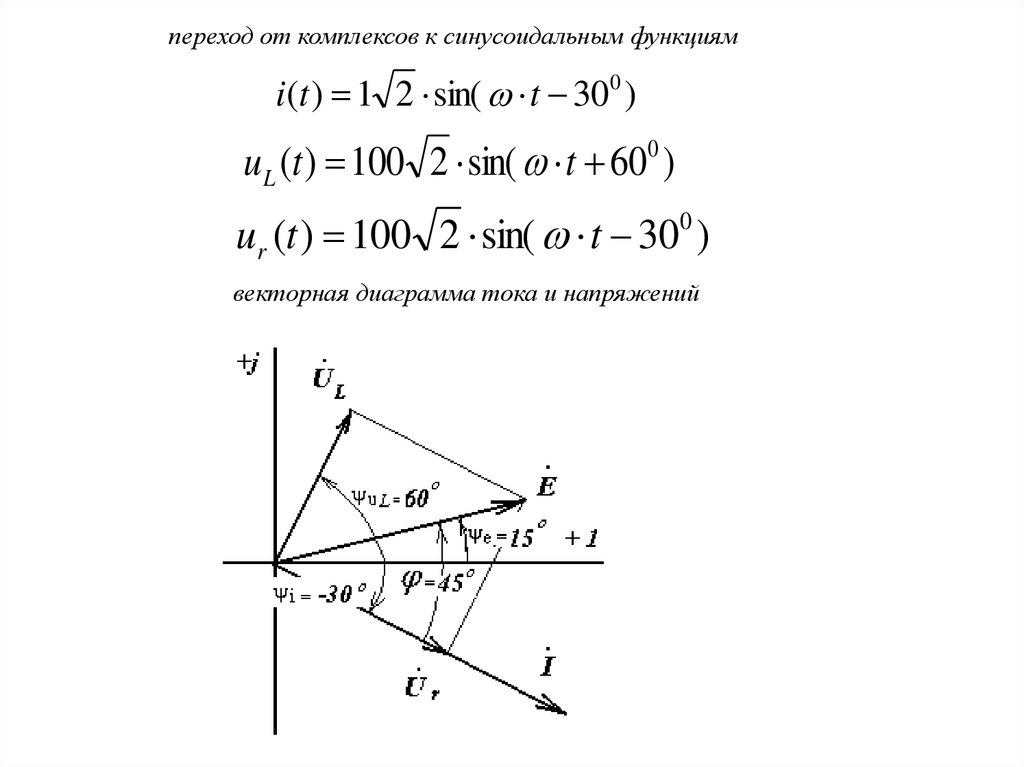
переход от комплексов к синусоидальным функциям
i (t ) 1 2 sin( t 300 )
u L (t ) 100 2 sin( t 60 )
0
ur (t ) 100 2 sin( t 300 )
векторная диаграмма тока и напряжений

23.

Алгоритм расчета токов в сложной цепи комплексным методом
Для расчета цепей в гармоническом режиме рекомендуется
следующий алгоритм действий:
1. От мгновенных значений заданных источников перейти к
комплексам действующих значений. Перевести пассивные
элементы ЭЦ в комплексные сопротивления.
2. Используя известные правила составления системы уравнений
записать алгебраические уравнения для комплексов действующих
значений токов.
3. Решить систему уравнений и найти комплексы токов в ветвях.
4. Записать мгновенные значения найденных реакций.

24.

Для расчета токов в сложной цепи можно использовать : законы Кирхгофа, МКТ,
МУП, МЭГ

25.

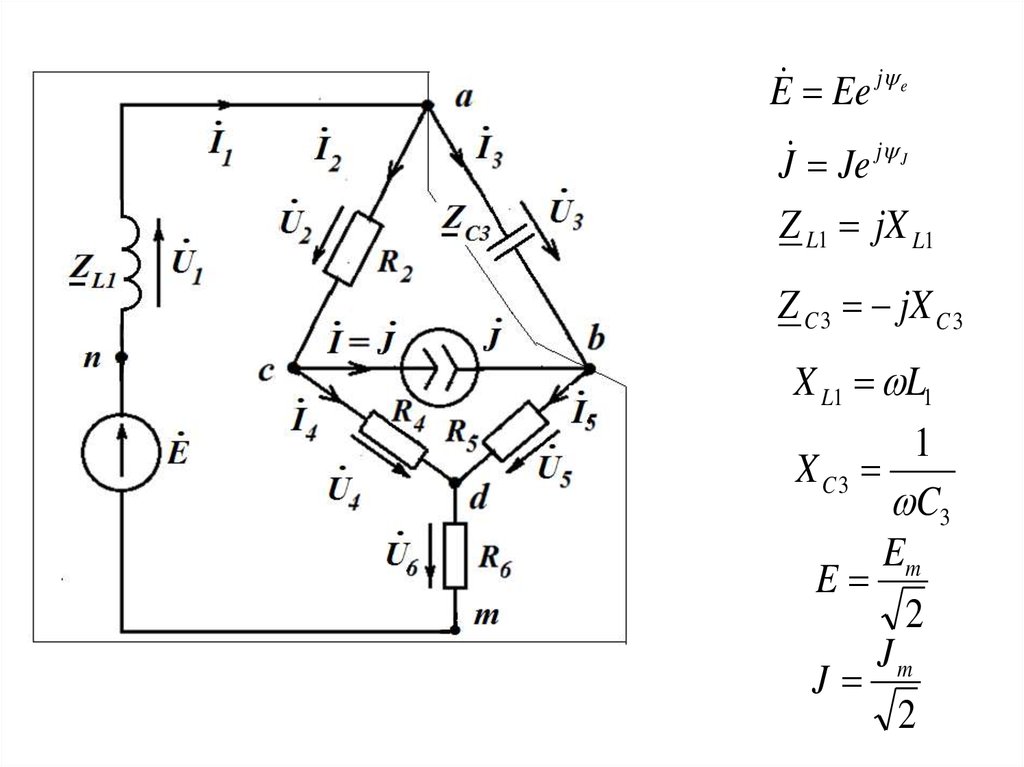
Для изображенной выше сложной цепи при заданных значениях:
J (t ) J m sin( t J )
e(t ) Em sin( t u )
R2
R4
R5
R6
L1
C3
требуется рассчитать синусоидальные токи в ветвях ЭЦ
Расчет по законам Кирхгофа
1. Изобразим схему цепи в комплексной форме и представим исходные данные в
комплексной форме

26.

E Ee j e
J Je j J
Z L1 jX L1
Z C 3 jX C 3
X L1 L1
1
X C3
C3
Em
E
2
Jm
J
2

27.

2. Расставим в схеме стрелки токов и напряжений в комплексной форме
3. Составим систему расчетных уравнений по законам Кирхгофа в комплексной
форме
Для изображенной комплексной схемы независимых узлов - 3, независимых контуров
- 2, неизвестных токов - 5. Следовательно , по 1 закону Кирхгофа составляется 3
уравнения, по 2 закону - 2 уравнения.
Узел
a:
Узел
b:
Узел
c:
Контур
Контур
I 1 I 2 I 3 0
I 3 J I 5 0
I J I 0
2
4
U 1 U 2 U 4 U 6 E
U 3 U 5 U 4 U 2 0

28.

С учетом уравнений связи ( закона Ома в комплексной форме) уравнения по 2 закону
Кирхгофа запишутся в виде
I 1 ( R6 Z L1 ) I 2 R2 I 4 R4 E
I 3 Z C 3 I 5 R5 I 4 R4 I 2 R2 0
4. Решить систему расчетных уравнений по законам Кирхгофа в комплексной форме,
используя матричную форму записи уравнений ,на ЭВМ или ручным расчетом
5. Перейти от комплексов действующих значений токов к мгновенным значениям
(синусоидальным функциям времени)

29.

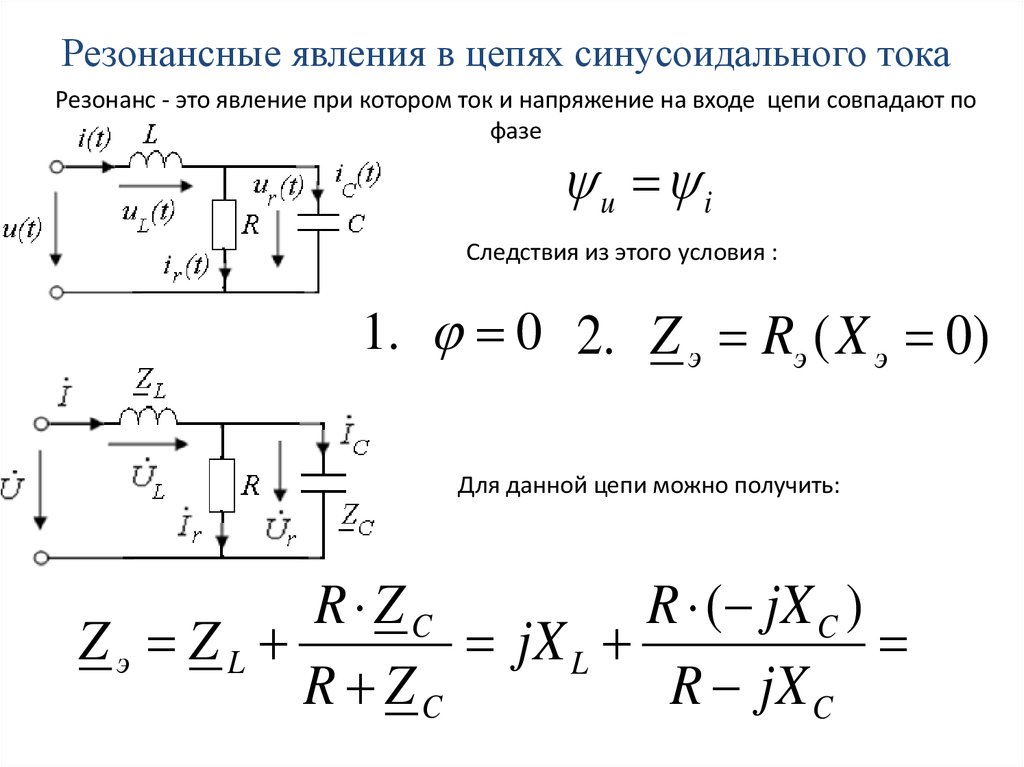
Резонансные явления в цепях синусоидального тока
Резонанс - это явление при котором ток и напряжение на входе цепи совпадают по
фазе
u i
Следствия из этого условия :
1. 0 2. Z э Rэ ( X э 0)
Для данной цепи можно получить:
R ( jX C )
R ZC
Zэ ZL
jX L
R ZC
R jX C

30.

R ( jX C ) ( R jX C )
RX C2
R2 X C
jX L
2
j( X L 2
)
2
2
( R jX C )( R jX C ) R X C
R XC
Rэ jX э
Условие резонанса для данной цепи :
2
Xэ 0
R XC
(X L 2
) 0
2
R XC

31.

резонанс в последовательном колебательном
контуре ( резонанс напряжений)
e t E m sin t
1
Z j R j L
C
I
1
C
R
L
E
1
R j L
C
E
1
R L
C
2
Условие резонанса :
1
L
0
C
X L XC
2
e
jarctg

32.

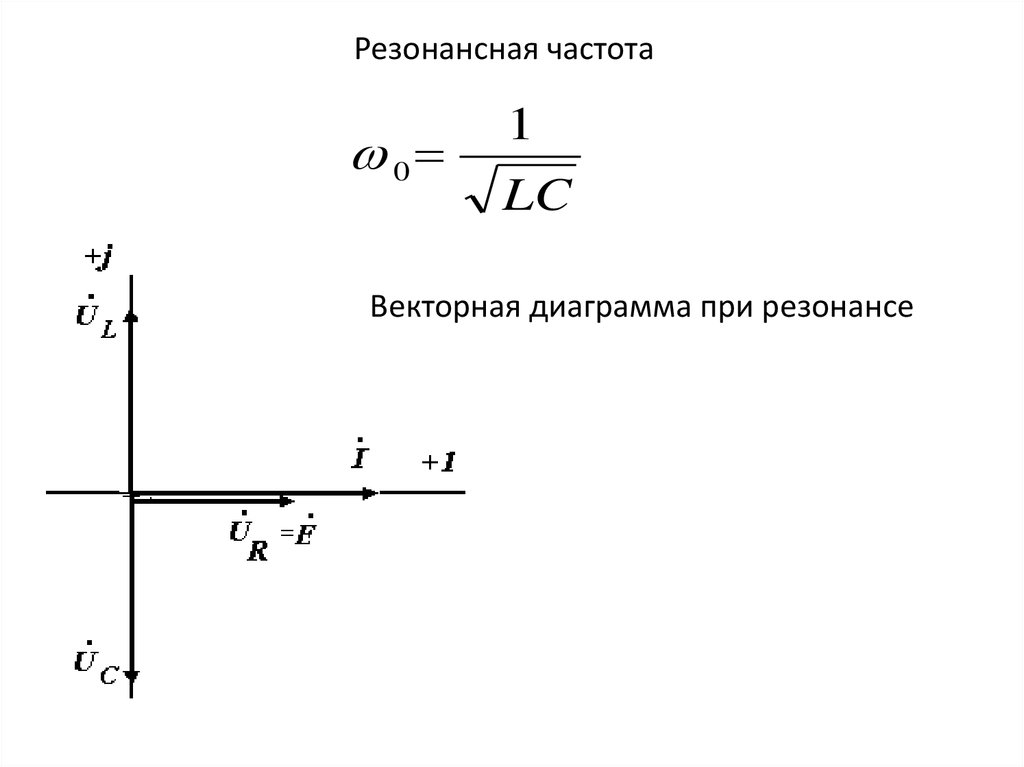
Резонансная частота
0
1
LC
Векторная диаграмма при резонансе

33.

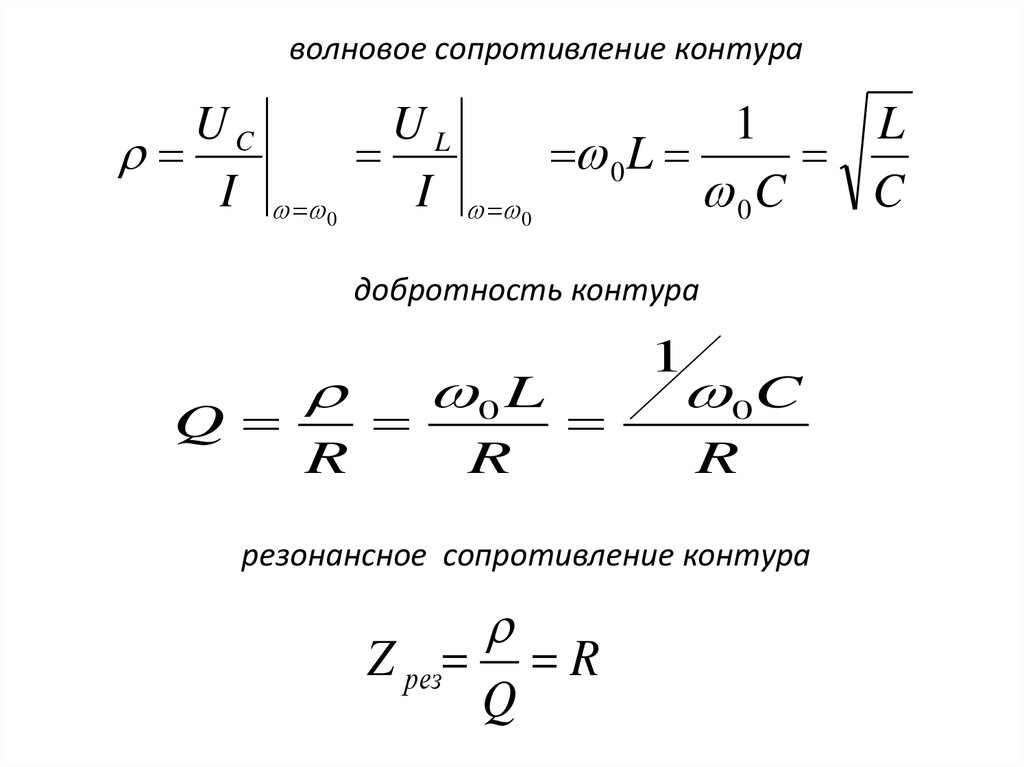
волновое сопротивление контура
UC
I
0
UL
I
0
1
L
0 L
0C
C
добротность контура
Q
R
0 L
R
1
0 C
R
резонансное сопротивление контура
Z рез R
Q

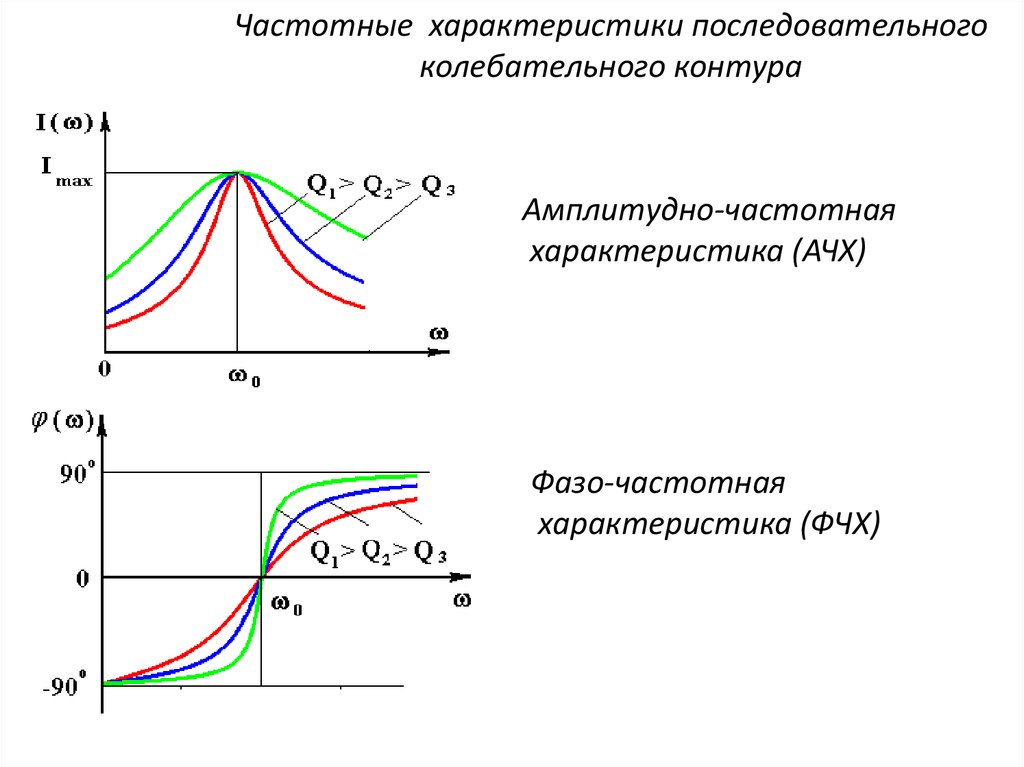
34.

Частотные характеристики последовательного
колебательного контура
Амплитудно-частотная
характеристика (АЧХ)
Фазо-частотная
характеристика (ФЧХ)

35.

резонанс в параллельном колебательном контуре
( резонанс токов)
J (t ) J msin t
Комплексная проводимость
Y j G j ( C 1
L)
Условие резонанса
( C 1
) 0 bL bC
L
резонансная частота
0
1
LC

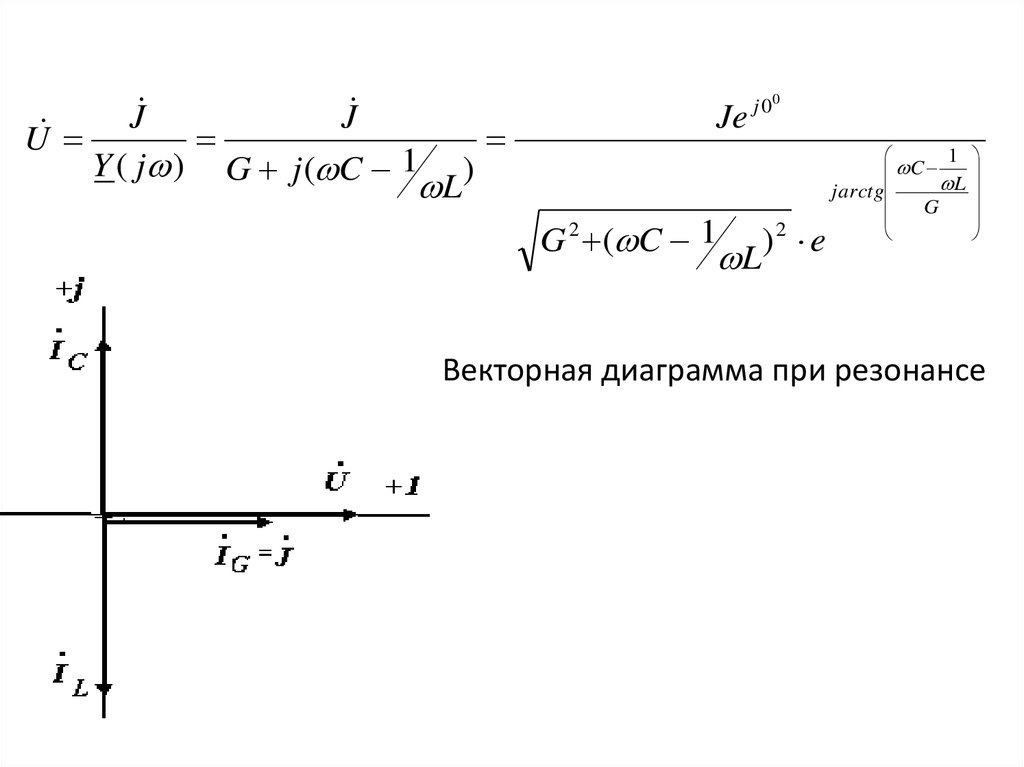
36.

J
J
U
Y ( j ) G j ( C 1
L
)
Je
G 2 ( C 1
j 00
L
)2 e
1
C
L
jarctg
G
Векторная диаграмма при резонансе

37.

волновое сопротивление контура
U
IL
0
U
IC
0
1
L
0 L
0C
C
добротность контура
0C
1
1
Q
G
G 0 L
G
резонансное сопротивление контура
1
Z рез Q R
G

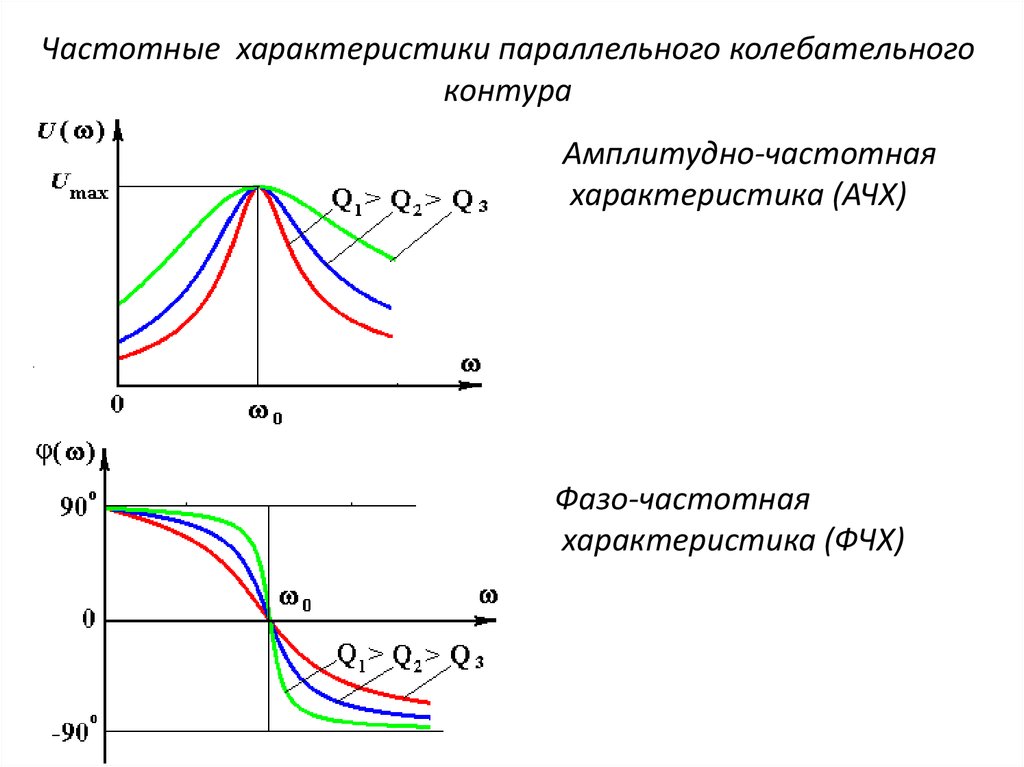
38.

Частотные характеристики параллельного колебательного
контура
Амплитудно-частотная
характеристика (АЧХ)
Фазо-частотная
характеристика (ФЧХ)

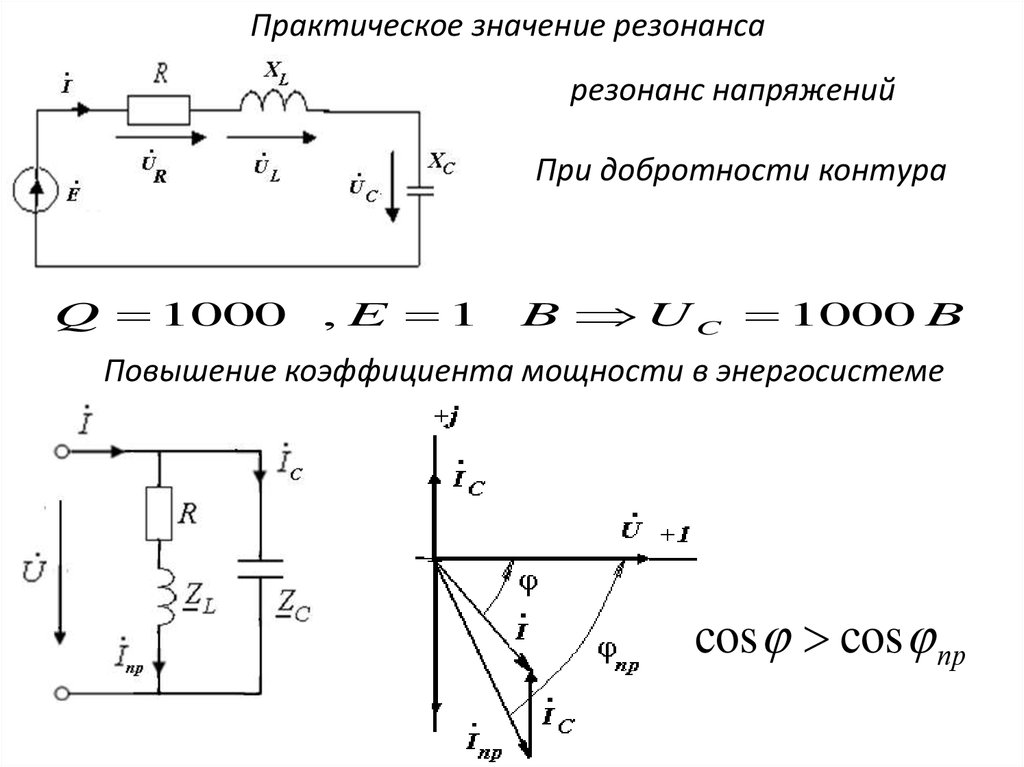
39.

Практическое значение резонанса
резонанс напряжений
При добротности контура
Q 1000
, E 1
B U C 1000 B
Повышение коэффициента мощности в энергосистеме
cos cos пр