Физика колебаний и волн

1.

Кафедра физики
ЛЕКЦИЯ 7
ПЛАН ЛЕКЦИИ
ФИЗИКА КОЛЕБАНИЙ И ВОЛН
• Общие представления о колебательных и волновых процессах.
• Гармонические колебания и их характеристики.
Гармонический осциллятор.
• Примеры гармонических осцилляторов. Математический
маятник
Общая физика. Физика колебаний и волн
1

2.

Кафедра физики
ФИЗИКА КОЛЕБАНИЙ И ВОЛН
Общие представления о колебательных и волновых процессах.
Колебания - это процессы, повторяющиеся во времени.
Колебательные процессы наблюдаются в системах различной
физической природы. Примеры: колебания груза на пружине,
колебания маятника, колебания тока в электрическом контуре и т. д.
В системах с бесконечным числом степеней свободы (сплошная
среда) колебательный процесс распространяется в пространстве. В
пространстве распространяется волна. Волна характеризуется
периодичностью как во времени, так и в пространстве. Примеры:
звуковые волны, электромагнитные волны и т.д.
Общая физика. Физика колебаний и волн
2

3.

Кафедра физики
ФИЗИКА КОЛЕБАНИЙ И ВОЛН
Общие представления о колебательных и волновых процессах.
Использование колебательных процессов:
- часы (механические и электронные);
- радиоприемники и телевизоры (колебательные контуры);
- связь (электромагнитные волны);
- другое.
Типы колебаний: свободные и вынужденные, автоколебания и
параметрические колебания.
Свободные (собственные) - колебания, которые развиваются в
системе, представленной самой себе после того, как она была
выведена из состояния равновесия. Совершаются за счет
первоначально сообщенной энергии. Пример: колебания груза на
пружине в поле сил тяготения.
Общая физика. Физика колебаний и волн
3

4.

Кафедра физики
ФИЗИКА КОЛЕБАНИЙ И ВОЛН
Общие представления о колебательных и волновых процессах.
Вынужденные - колебания, в процессе которых происходит
периодическое воздействие внешнего источника энергии. Пример –
электромагнитные колебания в контуре, куда включена
периодическая ЭДС.
Автоколебания поддерживаются за счет внешнего источника
энергии. Но: автоколебательная система сама управляет внешними
воздействиями, обеспечивая поступление энергии в такт с
колебаниями. Пример – механические часы. Храповой механизм
часов подталкивает маятник в такт с его колебаниями. Внешний
источник энергии - сжатая пружина либо опускающийся груз.
Параметрические колебания. Внешнее воздействие периодически
изменяет какой либо параметр системы, определяющий ее свойства.
Пример: в процессе колебаний маятника может периодически
изменяться длина нити, на которой подвешен маятник.
Общая физика. Физика колебаний и волн
4

5.

Кафедра физики
ФИЗИКА КОЛЕБАНИЙ И ВОЛН
Гармонические колебания и их характеристики
Колебания различной природы подчиняются одинаковым законам.
Пример: колебания груза, подвешенного на пружине, и изменение
заряда конденсатора в колебательном контуре происходят по одному
и тому же закону.
Гармонические колебания - колеблющаяся величина изменяется со
временем по закону косинуса (синуса).
Наиболее простой вид колебаний. Изучение
колебаний важно по следующим причинам:
гармонических
а) колебания, встречающиеся в природе и технике, часто имеют
характер, близкий к гармоническому;
б) различные периодические процессы можно представить как
наложение периодических колебаний.
Общая физика. Физика колебаний и волн
5

6.

Кафедра физики
ФИЗИКА КОЛЕБАНИЙ И ВОЛН
Гармонические колебания и их характеристики
Гармонические колебания некоторой величины x описываются
уравнениями вида:
x A cos 0 t 01
или
x A sin 0 t 02
где A - амплитуда колебания, т.е. наибольшее положительное
отклонение величины x от ее значения в состоянии равновесия;
- круговая или циклическая частота;
0 t 01 и 0 t 02 - фазы колебаний,
характеризующие текущее отклонение величины x от равновесия.
При t 0 01 или 02 , т.е.
фазы колебаний.
Общая физика. Физика колебаний и волн
01 и 02 - это начальные
6

7.

Кафедра физики
ФИЗИКА КОЛЕБАНИЙ И ВОЛН
Гармонические колебания и их характеристики
2π
Связь между параметрами
ω 2 πυ
гармонических колебаний:
T
где - частота колебаний (количество колебаний в единицу
времени), T - период колебаний, или время полного колебания.
Скорость и ускорение колеблющейся материальной точки.
x A cos 0 t
dx
v
A 0 sin 0 t A 0 cos 0 t
dt
2
d2x
a 2 A 02 cos 0 t A 02 cos 0 t
dt
Скорость и ускорение колеблющейся точки изменяются со
временем по гармоническому закону.
Общая физика. Физика колебаний и волн
7

8.

Кафедра физики
ФИЗИКА КОЛЕБАНИЙ
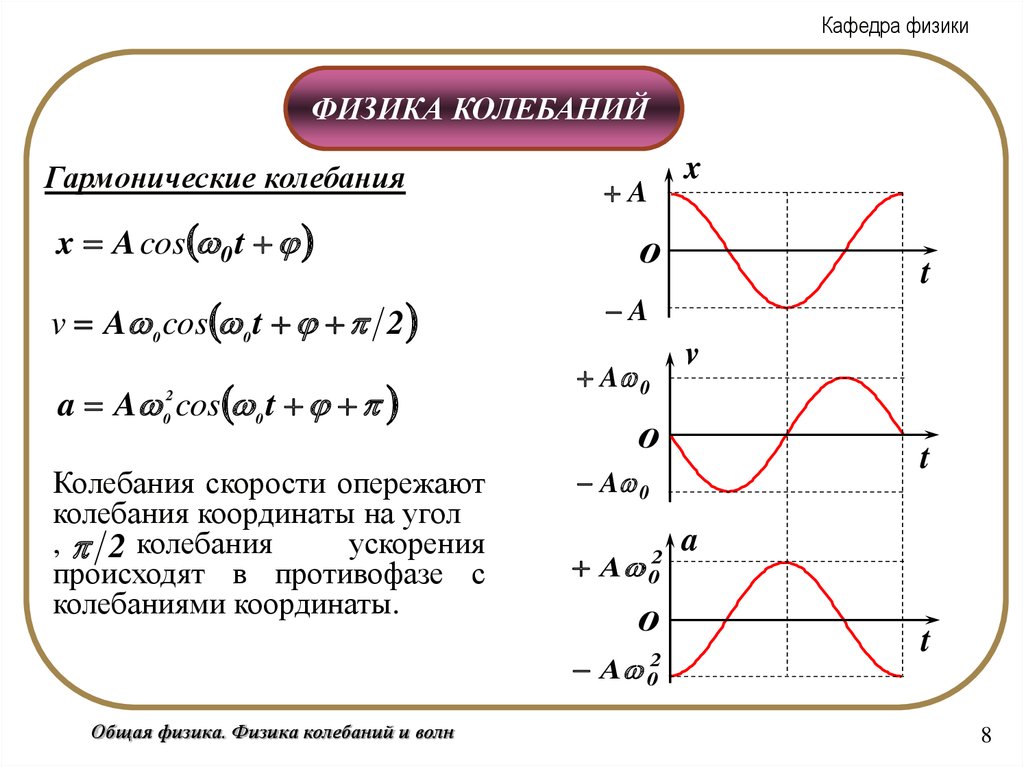
Гармонические колебания
A
x A cos 0 t
0
v A 0 cos 0 t 2
a A 0 cos 0 t
2
x
t
A
A 0
v
0
Колебания скорости опережают
колебания координаты на угол .
, 2 колебания
ускорения
происходят в противофазе с
колебаниями координаты.
A 0
A 02
0
Общая физика. Физика колебаний и волн
t
A 02
a
t
8

9.

Кафедра физики
ФИЗИКА КОЛЕБАНИЙ
Гармонические колебания
Кинетическая энергия колеблющейся материальной точки массой m:
mv 2 m 02 A 2
K
sin 2 0 t
2
2
Произведем простые тригонометрические преобразования для того,
чтобы иметь в правой части cos . Воспользуемся формулой из
тригонометрии:
1 cos 2
sin
,
2
В итоге получим:
sin 2
1 cos 2
2
m 02 A 2
1 cos 2 0 t
K
4
Общая физика. Физика колебаний и волн
9

10.

Кафедра физики
ФИЗИКА КОЛЕБАНИЙ
Гармонические колебания
Для определения потенциальной энергии П материальной точки,
запишем выражение для силы , действующей
на точку. По второму
F
закону Ньютона
F ma mAω02 cos ω0 t
Поскольку cos ω0 t x , F mω02 x .
Такая зависимость характерна для упругой силы. Работа этой силы
при бесконечно малом изменении x равна приращению
потенциальной энергии со знаком минус:
2
2
2
2
mω
x
mω
A
0
0
П - Fdx mω02 xdx
cos 2 ω0 t
2
2
0
0
x
x
Общая физика. Физика колебаний и волн
10

11.

Кафедра физики
ФИЗИКА КОЛЕБАНИЙ
Гармонические колебания
mω02 A 2
П
cos 2 ω0 t
2
Произведем преобразования по аналогии с выводом формулы для К.
Воспользуемся соотношением из тригонометрии:
1 cos 2
cos
,
2
В итоге получим:
1 cos 2
сos
2
2
mω02 A 2
1 cos 2 ω0 t
П
4
2
Полная энергия:
mω0 A
E K П
2
Общая физика. Физика колебаний и волн
2
m 02 A 2
1 cos 2 0 t
K
4
П
mω02 A 2
1 cos 2 ω0 t
4
11

12.

Кафедра физики
ФИЗИКА КОЛЕБАНИЙ
Гармонические колебания
m A
K
2
0
2
1 cos 2 t
0
42 2
mω0 A
1 cos 2 ω0 t
П
4
mω02 A 2
E K П
2
A
x
0
t
A
E
E
2
К
Кинетическая и потенциальная энергии
периодически изменяются от 0 до E по
0
гармоническому закону с частотой 2 0.
Колебания
кинетической
энергии E П
происходят в противофазе с колебаниями
потенциальной энергии, а их сумма в любой E
момент времени одинакова (упругая сила 2
консервативна, следовательно, выполняется 0
закон сохранения энергии).
Общая физика. Физика колебаний и волн
t
t
12

13.

Кафедра физики
ФИЗИКА КОЛЕБАНИЙ
Гармонический осциллятор
Любую колебательную систему называют осциллятором. Если
поведение осциллятора подчиняется гармоническому закону, то
гармоническим осциллятором.
Определим вид уравнения гармонического осциллятора. Для этого
используем вторую производную от уравнения движения
колеблющейся материальной точки:
d2x
2
A
0 cos 0 t
2
dt
d2x
2
Поскольку A cos 0 t x , то
0x 0
2
dt
получим выражение вида
Это дифференциальное уравнение гармонических колебаний.
Решение этого уравнения:
Общая физика. Физика колебаний и волн
x A cos 0 t
13

14.

Кафедра физики
ФИЗИКА КОЛЕБАНИЙ
Гармонический осциллятор
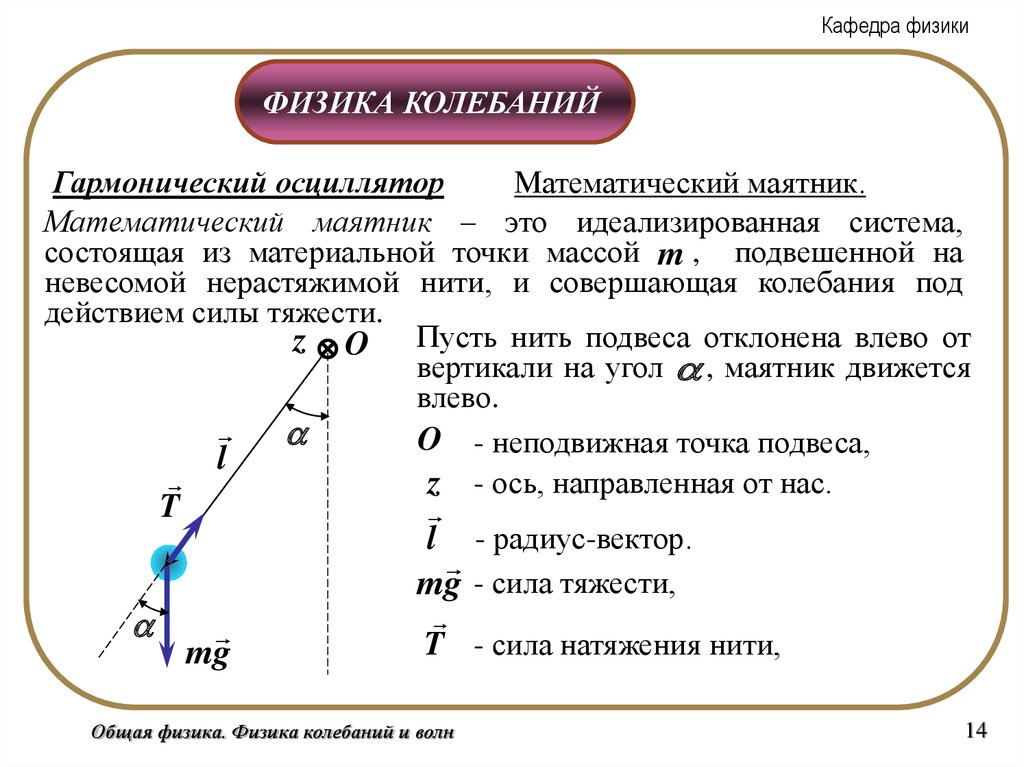
Математический маятник.
Математический маятник – это идеализированная система,
состоящая из материальной точки массой m , подвешенной на
невесомой нерастяжимой нити, и совершающая колебания под
действием силы тяжести.
z O Пусть нить подвеса отклонена влево от
вертикали на угол , маятник движется
влево.
O - неподвижная точка подвеса,
l
z - ось, направленная от нас.
T
mg
l - радиус-вектор.
mg - сила тяжести,
T - сила натяжения нити,
Общая физика. Физика колебаний и волн
14

15.

Кафедра физики
ФИЗИКА КОЛЕБАНИЙ
Гармонический осциллятор
z
T
l
O
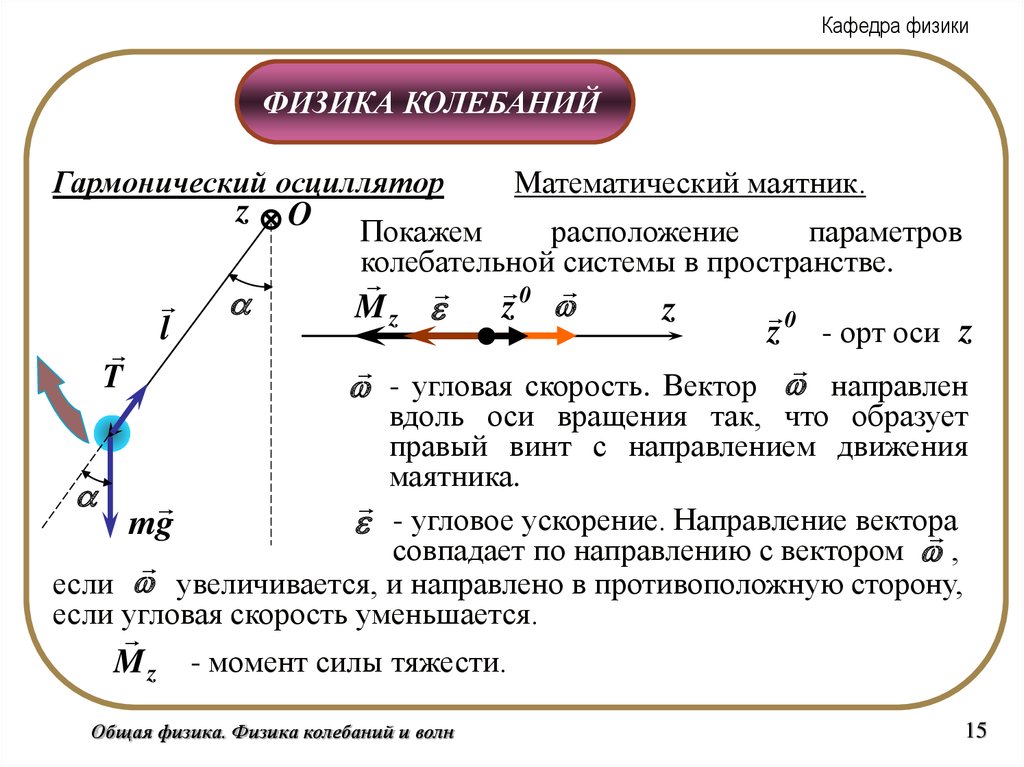
Математический маятник.
Покажем
расположение
параметров
колебательной системы в пространстве.
Mz
z0
0
z - орт оси z
- угловая скорость. Вектор направлен
z
вдоль оси вращения так, что образует
правый винт с направлением движения
маятника.
- угловое ускорение. Направление вектора
mg
совпадает
по
направлению
с
вектором
,
если увеличивается, и направлено в противоположную сторону,
если угловая скорость уменьшается.
M z - момент силы тяжести.
Общая физика. Физика колебаний и волн
15

16.

Кафедра физики
ФИЗИКА КОЛЕБАНИЙ
Гармонический осциллятор
z
T
l
O
Mz
Математический маятник.
0
z
z
Пренебрежем силами трения и сопротивления
среды. Получим уравнение движения.
Основной закон вращательного движения
твердого тела относительно оси z :
J z M z ,
mg
точки относительно оси z .
J z - момент инерции
Момент силы T относительно оси z равен нулю.
Момент силы тяжести M z стремится возвратить
маятник в положение равновесия.
Общая физика. Физика колебаний и волн
16

17.

Кафедра физики
ФИЗИКА КОЛЕБАНИЙ
Гармонический осциллятор
z
T
l
Mz
O
Математический маятник.
z0
z
J z M z
Величины, входящие в уравнение запишем
J z M z ,
следующим образом:
M z l , mg , M z lmg sin ,
d 2 0
2 z , J z ml 2
dt
d 0
z ,
dt
mg
Отсюда основной закон вращательного движения в проекции на
ось z может быть записан в виде:
2
d
2
ml
mgl sin ,
2
dt
Общая физика. Физика колебаний и волн
d 2
g
sin
2
l
dt
17

18.

Кафедра физики
ФИЗИКА КОЛЕБАНИЙ
Гармонический осциллятор
Математический маятник.
d 2
g
Знак «минус» означает, что действие силы
sin
тяжести направлено против движения маятника.
l
dt 2
Окончательно получим:
d 2
2
0 sin 0 , где 0
2
dt
g
l
Это нелинейное дифференциальное уравнение, описывающее
движение математического маятника при любой величине угла
отклонения от вертикали.
Если рассматривать малые отклонения маятника от положения
равновесия 1 , то получим дифференциальное уравнение
гармонических колебаний (при 1 sin ):
d 2
2
0 0
2
dt
Общая физика. Физика колебаний и волн
18

19.

Кафедра физики
ФИЗИКА КОЛЕБАНИЙ
Гармонический осциллятор
d 2
2
0 0
2
dt
Математический маятник.
В этом уравнении 0 имеет смысл
собственной круговой частоты малых 0
колебаний математического маятника.
g
l
Период этих колебаний определяется по формуле
T 2π
l
g
Решение полученного уравнения:
0 cos 0 t
Общая физика. Физика колебаний и волн
19

20.

Кафедра физики
ФИЗИКА КОЛЕБАНИЙ
Гармонический осциллятор
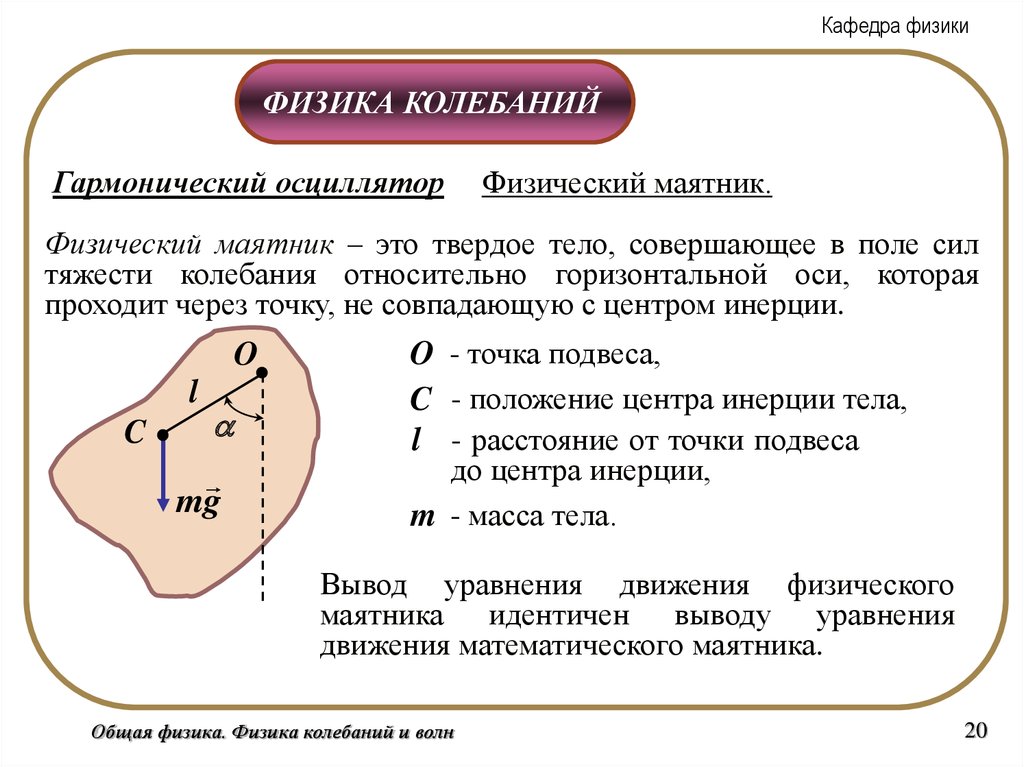
Физический маятник.
Физический маятник – это твердое тело, совершающее в поле сил
тяжести колебания относительно горизонтальной оси, которая
проходит через точку, не совпадающую с центром инерции.
O
l
C
mg
O - точка подвеса,
C - положение центра инерции тела,
l - расстояние от точки подвеса
до центра инерции,
m - масса тела.
Вывод уравнения движения физического
маятника идентичен выводу уравнения
движения математического маятника.
Общая физика. Физика колебаний и волн
20

21.

Кафедра физики
ФИЗИКА КОЛЕБАНИЙ
Гармонический осциллятор
O
l
C
Физический маятник.
Отличие - в общем случае невозможно записать
вид выражения для момента инерции маятника.
mg
Jz
d 2
dt
2
mgl sin
Пусть собственная частота колебаний ω
физического маятника выражается как 0
mgl
Jz
Получим такие же уравнения, как и для математического маятника:
d 2
2
0 0,
2
dt
решение:
Общая физика. Физика колебаний и волн
0 cos 0 t
21

22.

Кафедра физики
ФИЗИКА КОЛЕБАНИЙ
Гармонический осциллятор Пружинный маятник.
Пружинный маятник – это колебательная система, состоящая из
груза массой m , подвешенного на абсолютно упругой пружине и
совершающего прямолинейные гармонические колебания в поле сил
тяжести под действием упругой силы.
Пусть груз сместился от положения
равновесия x 0 вниз и продолжает
движение вниз.
0
Fу
a
v
mg
x
На груз действует сила
тяжести mg и
сила упругости F у деформированной
пружины, пропорциональная смещению
.x от положения равновесия:
Fу kx
k - величина, называемая жесткостью
Общая физика. Физика колебаний и волн
пружины.
22

23.

Кафедра физики
ФИЗИКА КОЛЕБАНИЙ
Гармонический осциллятор
Пружинный маятник.
Закон
движения
пружинного маятника:
0
Fу
a
v
mg
x
Уравнение колебаний
маятника:
d2x
m 2 kx
dt
d2x
0 x 0
2
dt
Маятник совершает гармонические колебания
по закону
x A cos 0 t
с собственной круговой
частотой
k
0
m
Приведенные примеры показывают, что различные механические
системы
совершают
колебания,
которые
описываются
одинаковыми уравнениями, т.е. ведут себя аналогичным образом.
Общая физика. Физика колебаний и волн
23