Похожие презентации:
Механические колебания. Виды колебаний
1.
ГЛАВА I. МЕХАНИКА§15. Механические колебания
О. И. Лубенченко
НИУ МЭИ
Кафедра физики им. В. А. Фабриканта
2020
2.
§15. Механические колебания2
I. Виды колебаний
Колебания — ФЯ — периодические изменения какой-либо ФВ во времени.
Колебательная система — система тел, в которой происходят колебания.
Колебания
свободные
колебательная система
предоставлена самой себе
незатухающие
W = const
вынужденные
при периодическом внешнем
воздействии
затухающие
W ≠ const
W↓
II. Свободные незатухающие (собственные) колебания
Пружинный маятник — груз (МТ) массы m, который может колебаться на
пружине жёсткостью k.
Трения нет.
3.
§15. Механические колебанияII закон Ньютона: ma Fт N F упр
N
F упр
k
x
Fт
k
ω02
m
Fупр x kx
x : max kx
m
O
3
d2x
ax 2
dt
d2x
m 2 kx 0
dt
d2x k
x 0
2
dt
m
d2x
2
ω
x 0 — дифференциальное уравнение свободных
0
2
dt
гармонических колебаний
Общее решение: x t A cos ω0t φ — гармоническая функция
vx t
dx
Aω0 sin ω0t φ
dt
ax t
d vx
Aω02 cos ω0t φ
dt
Подставим начальные условия: при t = 0 x = x0, vx = 0
x 0 A cos φ
x0 A cos φ
0 Aω0 sin φ
vx 0 Aω0 sin φ
Частное решение: x t x0 cos ω0t
φ 0
A x0
4.
§15. Механические колебанияax t x0ω02 cos ω0t
vx t x0ω0 sin ω0t
vx
x0ω0
x
x0
π
ω0
0
4
3π
ω0
2π
ω0
π
2ω0
t
0
–x0
3π
2ω0
–x0ω0
ax
x0ω02
2π
ω0
0
x0ω02
π
ω0
3π
ω0
t
5π
2ω0
7π
2ω0
t
5.
§15. Механические колебания5
A — амплитуда колебаний — максимальное отклонение колеблющейся
величины от равновесного значения.
рад 1
ω0 — ФВ — циклическая частота
ω
0 с с
Выражение в скобках — фаза колебаний
φ — начальная фаза
Период T0 — ФВ — время, за которое колебательная система совершает одно
полное колебание.
Частота ν0 — ФВ — число полных колебаний в единичный промежуток
времени.
T0
2π
ω0
ν0
ω0 1
2π T0
ν0 Гц
Энергия колебаний (механическая энергия колебательной системы):
mv2 kx 2
W Wк Wп
const
2
2
6.
§15. Механические колебанияПРИМЕРЫ
1. Математический маятник
Математический маятник — МТ, подвешенная
⊙
z
на невесомой нерастяжимой нити в однородном
T
гравитационном поле.
l
II закон Ньютона: ma Fт T
φ n
a
n : man T Fт cos φ
m τ
τ : maτ Fт sin φ
Fт mg (закон всемирного тяготения)
Fт
d 2φ
aτ εz l
εz 2
dt
d 2φ
d 2φ g
m 2 l mg sin φ
sin φ 0
2
dt
dt
l
2
d
φ
g
2
При малых углах sin φ ≈ φ
ω
ω
φ
0
0
0
l
dt 2
T0
2π
ω0
T0 2π
l
g
6
7.
§15. Механические колебания7
2. Физический маятник
Физический маятник — ТТ, которое может
N
вращаться вокруг неподвижной горизонтальной оси,
⊗M
проходящей через точки этого тела, не являющиеся
⊙z
его ЦМ, в однородном гравитационном поле.
⊗ε
ОУДВД: Iε M Fт M N
d
φ
C
z : Iεz Fтd sin φ
Fт mg (закон всемирного тяготения)
m
Fт
d 2φ
εz 2
dt
d 2φ mgd
При малых углах sin φ ≈ φ
φ 0
2
dt
I
mgd
ω0
I
2π
T0
ω0
T0 2π
I
mgd
8.
§15. Механические колебанияIII. Свободные затухающие колебания
Рассмотрим пружинный маятник.
Сила вязкого трения F сопр r v
N
F упр
k
O
m v
x
F сопр
Fт
ω0
k
m
II закон Ньютона: ma Fт N F упр F сопр
d2x
dx
x : m 2 kx r
dt
dt
d 2 x r dx k
x 0
2
dt
m dt m
r
2β β — коэффициент затухания
m
d2x
dx
2
— дифференциальное уравнение свободных
2
β
ω
0x 0
2
dt
dt
затухающих колебаний
8
9.
§15. Механические колебания1. Сильное затухание (β ≥ ω0)
Общее решение:
β
x t A e
1
β 2 ω02 t
β
Ae
2
9
— апериодическое решение
β 2 ω02 t
x
λ2 2βλ ω02 0
x0
λ1,2 β β 2 ω02
x t A1e λ1t A2e λ2t
0
t
2. Слабое затухание (β < ω0)
Общее решение: x t A0e βt cos ωt φ
λ1,2 β i ω02 β 2
ω ω02 β 2 — циклическая частота затухающих колебаний
10.
§15. Механические колебания10
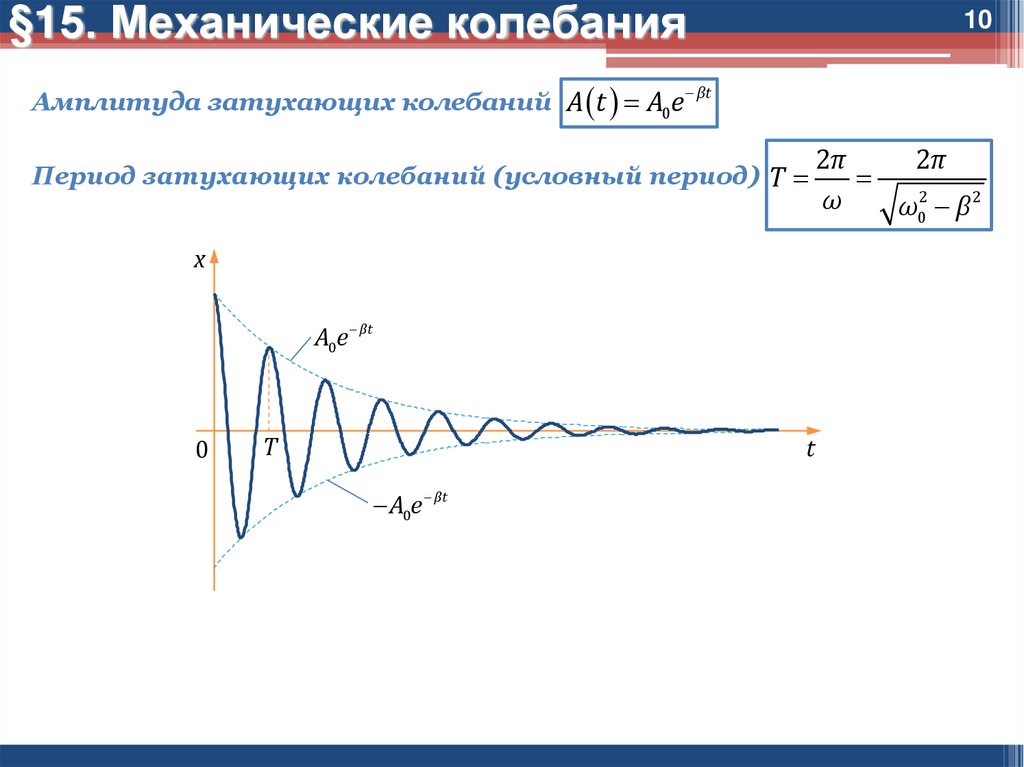
Амплитуда затухающих колебаний A t A0e βt
Период затухающих колебаний (условный период) T
x
A0e βt
0
T
t
A0e βt
2π
2π
ω
ω02 β 2
11.
§15. Механические колебания11
IV. Вынужденные колебания
Рассмотрим пружинный маятник, находящийся под воздействием,
описываемым периодической силой F F cosΩt
0
N
F упрm
k
ω0
O
F сопр
k
m
2β
II закон Ньютона:
v
ma Fт N F упр F сопр F
F
x
Fт
r
m
F0
f0
m
d2x
dx
x : m 2 kx r F0 cosΩt
dt
dt
F0
d 2 x r dx k
x
cosΩt
2
dt
m dt m
m
d2x
dx
2
— дифференциальное уравнение
2
β
ω
0 x f 0 cosΩt
2
dt
dt
вынужденных гармонических колебаний
Общее решение (при β < ω0): x t x1 t x2 t
общее решение
ОДУ
x1 t A1e βt cos ωt φ
частное решение
2
2
ω
ω
β
0
НДУ
x2 t A2 cos Ωt φ0
12.
§15. Механические колебания12
x1(t) быстро затухает циклическая частота вынужденных колебаний равна Ω
dx2
A2Ωsin Ωt φ0
dt
d 2 x2
2
A
Ω
cos Ωt φ0
2
2
dt
Ω2 A2 cos Ωt φ0 2βΩA2 sin Ωt φ0 ω02 A2 cos Ωt φ0 f0 cosΩt
f0 cosΩt f0 cos Ωt φ0 φ0 f0 cos Ωt φ0 cos φ0 sin Ωt φ0 sin φ0
Ω2 A2 ω02 A2 f0 cos φ0
2βΩA2 f0 sin φ0
tg φ0
f0 cos φ0
f0
f0
1
A2 2
ω0 Ω2 ω02 Ω2 1 tg 2 φ0 ω02 Ω2
A2
cos α β cos α cos β sin α sin β
1
1
2
4β Ω
ω
2
0
f0
ω
2
0
Ω
2
2βΩ
ω02 Ω2
2
4 β 2 Ω2
2
Ω
2
2
f0
ω
2
0
Ω
2
2
4 β 2 Ω2
13.
§15. Механические колебанияf
A2 0 02
ω0
22 2
1
2
2
2 2 ω0 Ω 2 Ω 8 β Ω
f0
0
32
2
ω2 Ω2 4β 2Ω2
0
dA2
A2 0
0
dΩ
13
2β 2Ω Ω ω02 Ω2 0
Ω 2β 2 ω02 Ω2 0
Ωmin = 0
Ωрез ω02 2β 2 — резонансная циклическая частота
Резонанс — ФЯ — резкое возрастание амплитуды вынужденных колебаний
при приближении циклической частоты вынуждающей силы к резонансной
циклической частоте.
14.
§15. Механические колебания14
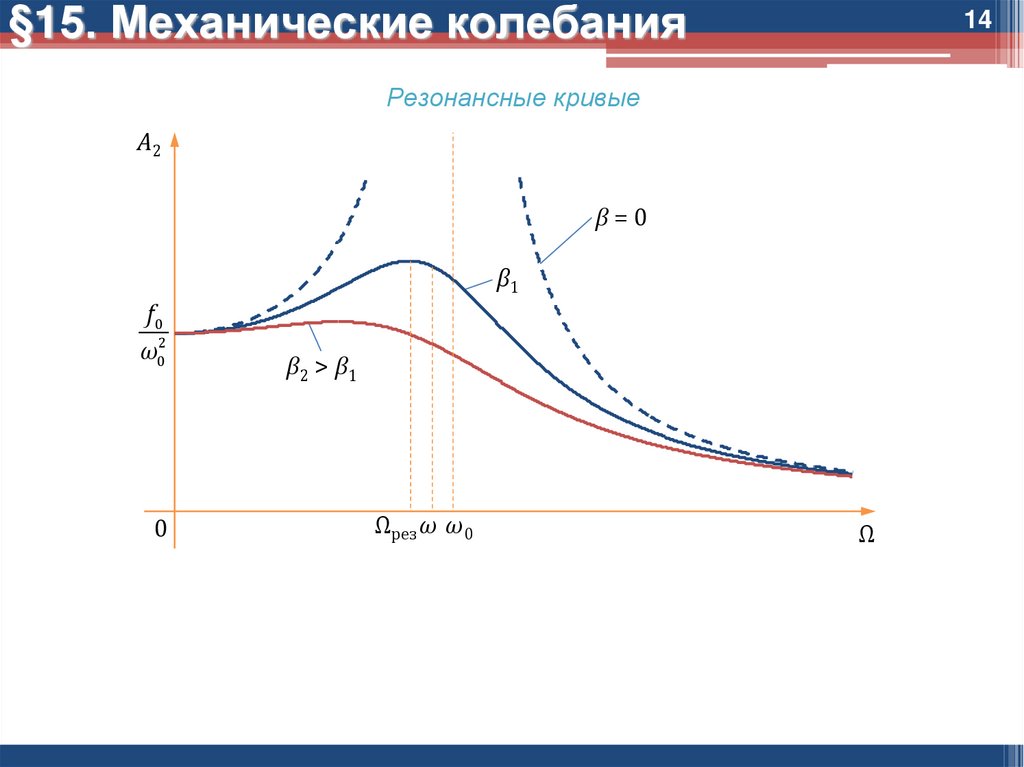
Резонансные кривые
A2
β=0
β1
f0
ω02
0
β2 > β1
Ωрез ω ω0
Ω












 Физика
Физика








