Похожие презентации:
Введение.Точка.Прямая.( Лекция № 1)
Введение.
Точка.
Прямая.
Лекция № 1 План лекции Введ ение12 Историческая справка3 Методы проецирования4 Точка5 Прямая линия Инженерная графика (Черчение) Начертательная геометрия.
Введ ение Входят в список дисциплин, составляющих основу инженерного образования.
Начертательная геометрия- наука о проекционных изображениях.
Предметом начертательной геометрии являются:
• Способы построения изображений пространственных форм на плоскости;
• Исследование геометрических свойств объектов по их изображениям.5 В инженерной графике изучают: методы изображения предметов;
правила выполнения и чтения чертежей деталей и сборочных единиц.
Литература Ляшков А.А., Куликов Л.К., Панчук К.Л.
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ (конспект лекций) Омск: Изд-во ОмГТУ, 2005
• Гордон В.О., Семенцов – Огиевский М.А.
Курс начертательной геометрии: учебник.
– М.: Высшая школа, 2007.
• Бубенников А.В.
Начертательная геометрия: учебник.
– М.: Высш.
шк., 1985.
• Фролов С.А.
Начертательная геометрия: учебник.
– М.: ИНФРА–М, 2007.
Историческая справка С древних времён человек старался сохранить образ увиденного.
Наскальная живопись, украшенные рисунками стены жилища, посуда, предметы быта – первые тому свидетельства.
Цивилизация развивалась, появились схемы и карты местности, изображение храмовых комплексов, жилых домов, военных сооружений, мостов, простых механизмов.
Потребовалась выработка и первых общих правил представления пространственной информации на плоскости.
Семь чудес света трудно представить без первых чертежей, рисунков и схем.
Египетские, греческие и римские учёные, изучая перспективу, пытались выработать некие правила представления имеющейся информации.
Эпоха Возрождения вызвала расцвет архитектуры, скульптуры, живописи.
Первые теоретические основы перспективы создал итальянский учёный Историческая справка Леон Баттиста Альберти (1404 -1472) Дополнил линейную перспективу учением "Об уменьшении цветов и отчётливости очертаний".
Историческая справка Леонардо да Винчи (1452 -1519) Ввел метод координат французский архитектор Историческая справка Жерар Дезарг (1593 -1662) 1795 г.
- появилась "Начертательная геометрия" Гаспара Монжа, им введено понятие «комплексный чертёж» и получены полностью обратимые изображения объемных (пространственных) объектов на плоскости.
Историческая справка Гаспар Монж (1746 -1818) Основоположник начертательной геометрии - Первый учебник по начертательной геометрии опубликован во Франции в 1798 г.
Россия .
Развитию начертательной геометрии способствовали А.
Рублёв, Дионисий, архитекторы В.Баженов, А.Ворончихин;
самоучки, механики- изобретатели И.
Ползунов, И.
Кулибин, И.
Моторин и другие.
1810 г.
– Карл Потье читает в С.-Петербурге первые лекции в Институте корпуса инженеров путей сообщения.
1821 г.
– Я.А.
Севастьянов (1796-1849) издает оригинальный курс начертательной геометрии на русском языке.
Историческая справка 1900 г.
– в Сибири, в Томском техническом институте курс начертательной геометрии прочитан Историческая справка Позже в России начертательная геометрия развивалась трудами Н.
Макарова, В.
Курдюмова, А.
Власова, Н.
Глаголева, Н.
Четверухина и многих других.
Валентином Николаевичем Джонсом 28(16)октября 1900г.
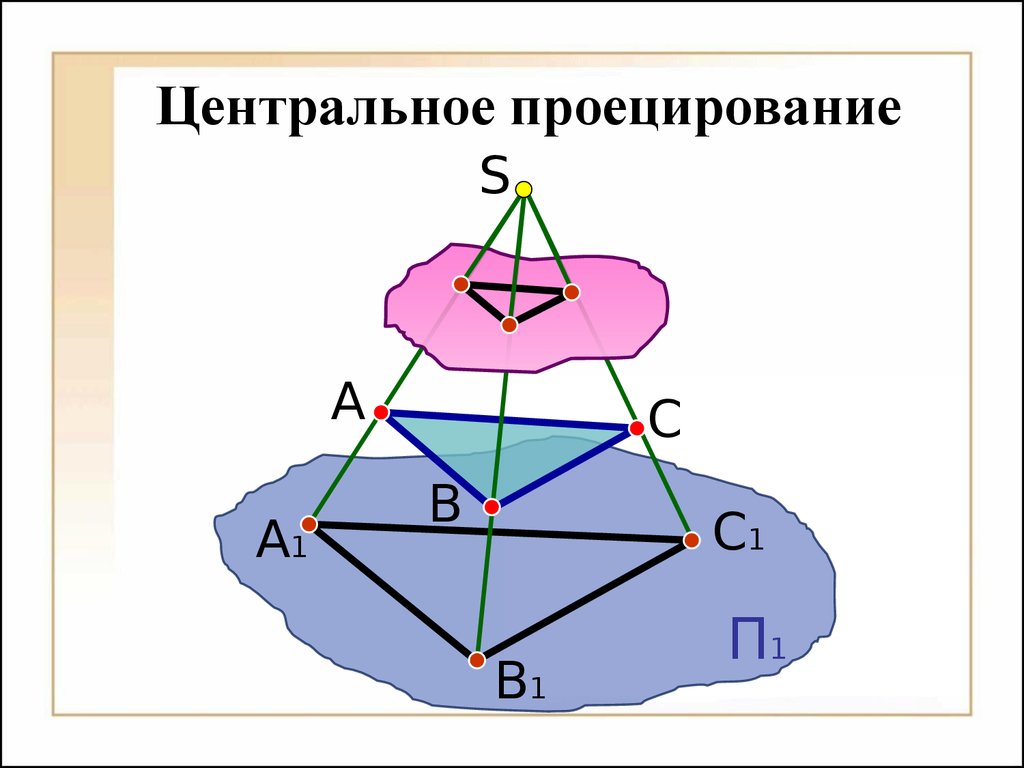
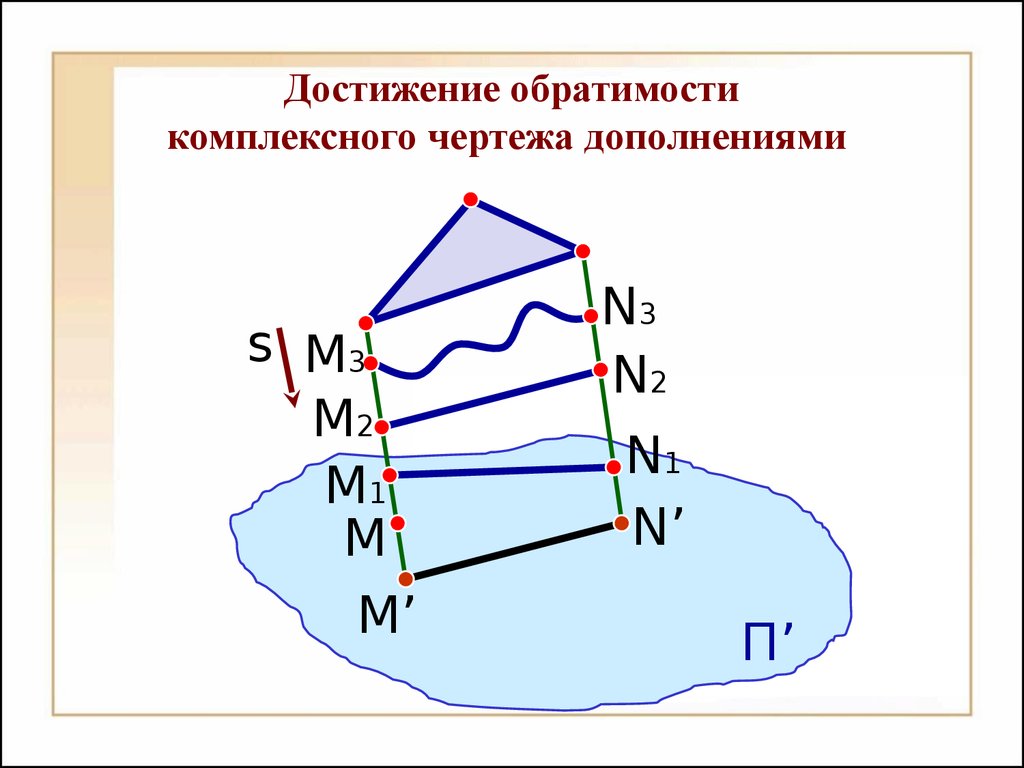
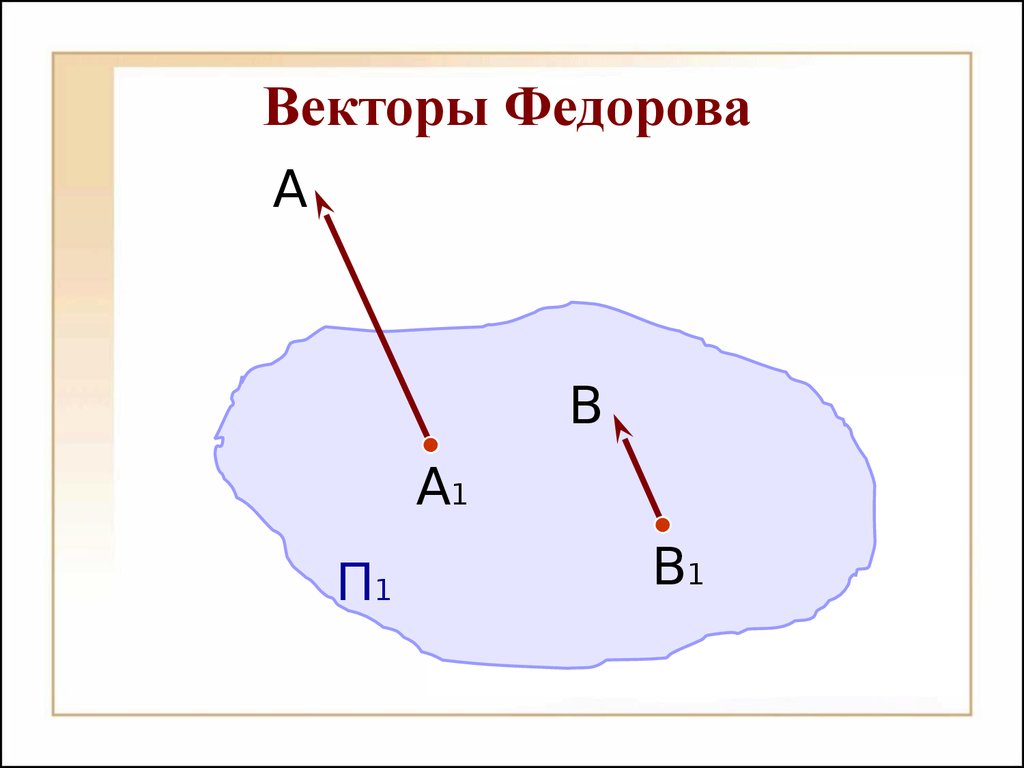
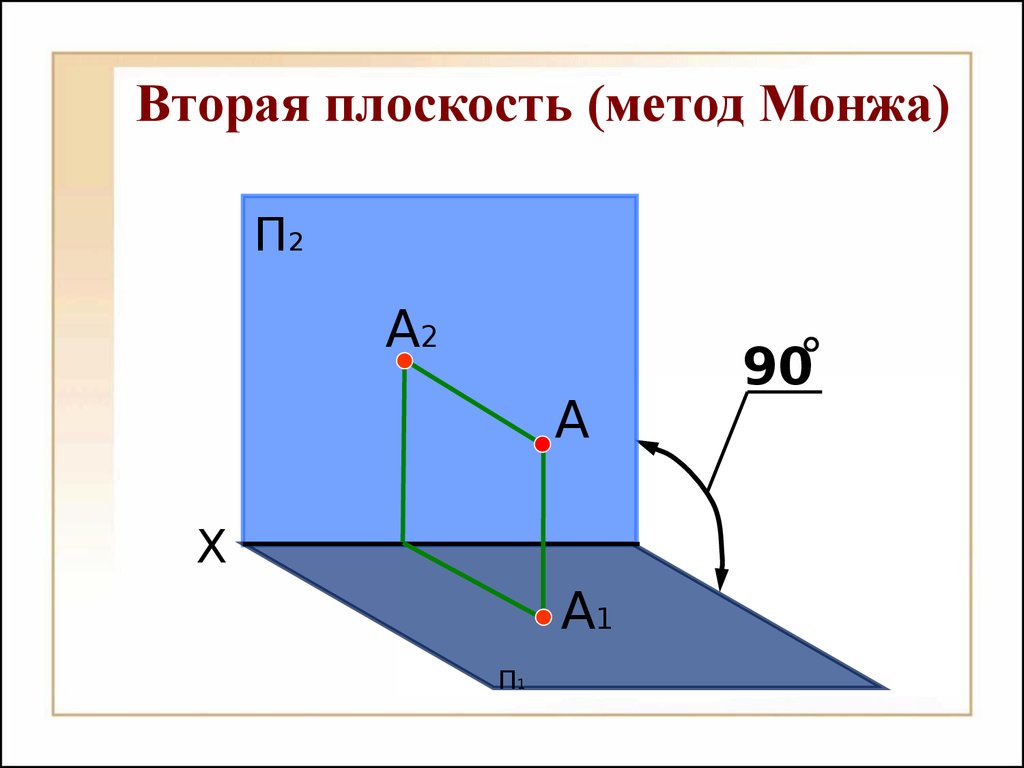
Методы проециро вания Методы проециро вания ЦЕНТРАЛЬНОЕ ПАРАЛЛЕЛЬНОЕП1А1В1С1ACBS Центральное проецированиеП1А1В1С1ACBSП1А1В1С1AC Параллельное проецированиеB º- прямоугольное проецирование ≠ º- косоугольное проецированиеs Достижение обратимости комплексного чертежа дополнениями П’ M’ N’MsM1N1M2N2M3N3 Числовые отметкиА6AП1BCB-4=C0 Векторы ФедороваП1А1В1АВ90 Вторая плоскость (метод Монжа)XП2П1А1А2 VIIIVIIVI-УXП1П2П3-XУZ-ZIIIOIVVIII Модель основных плоскостей проекций.
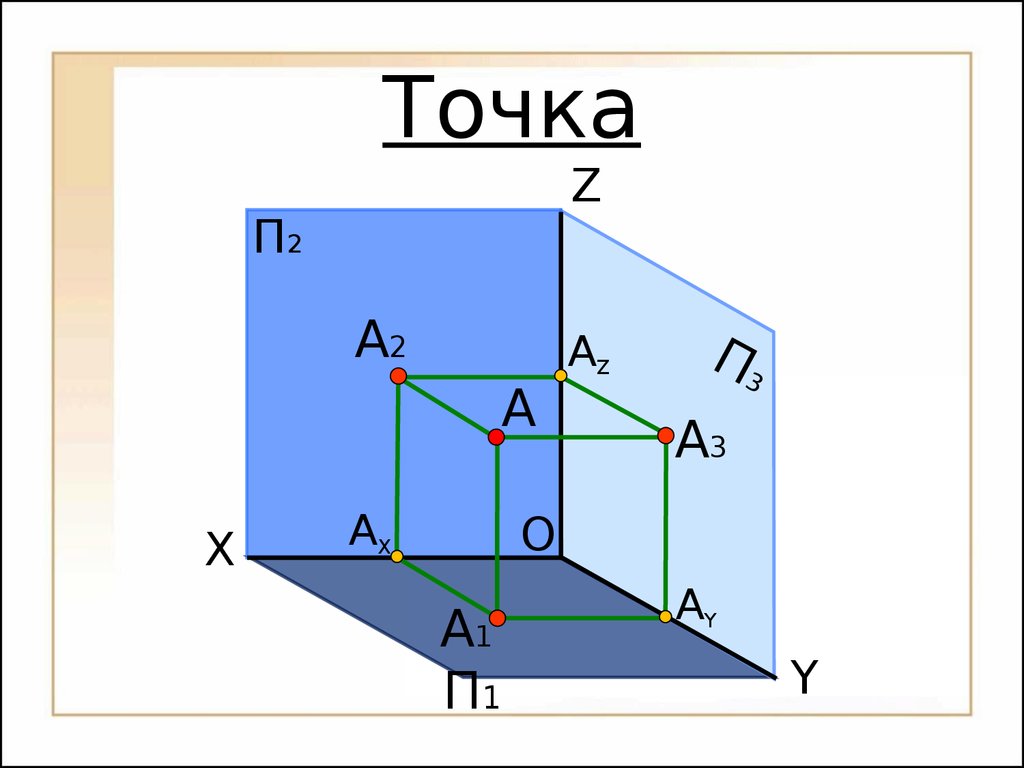
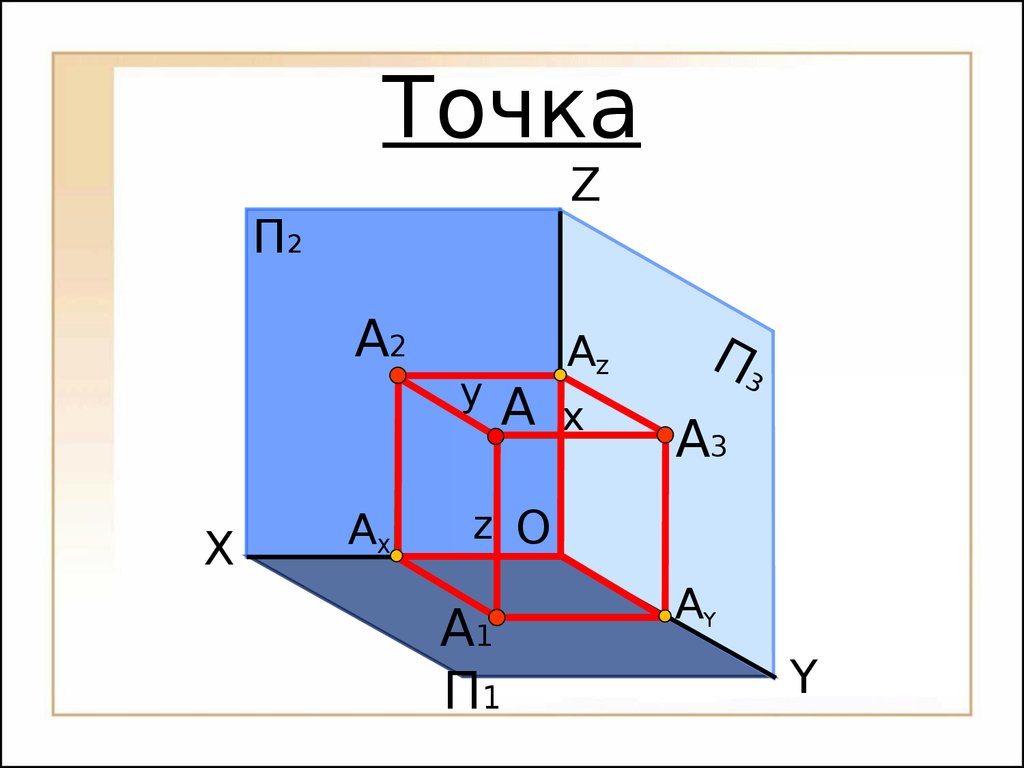
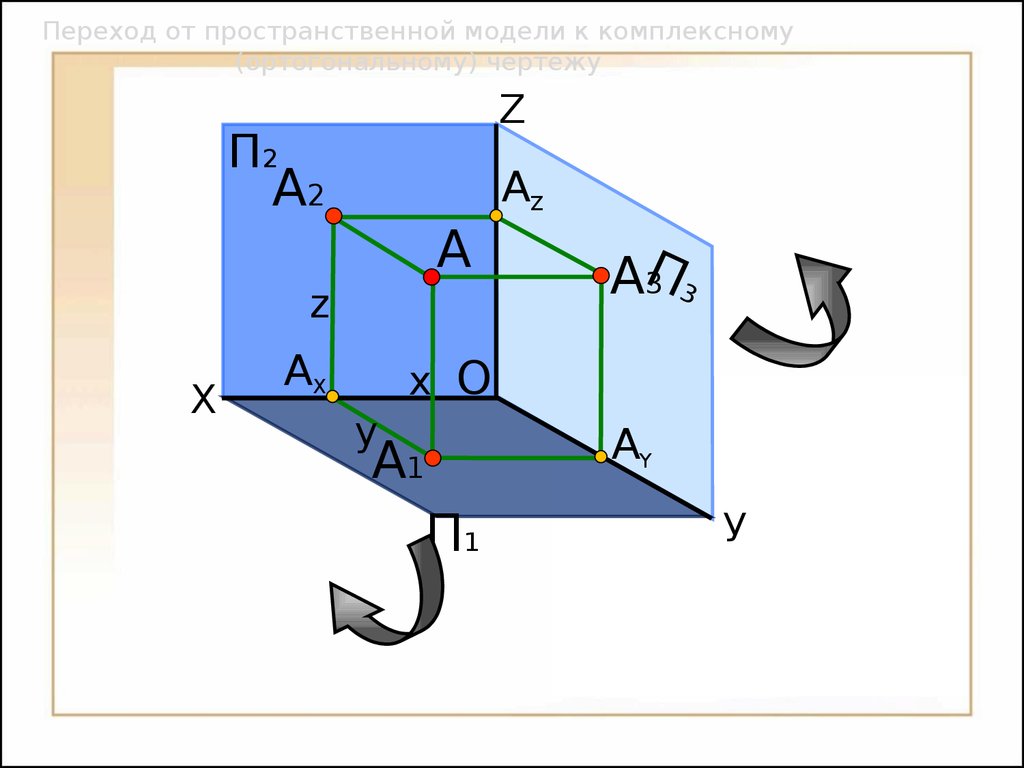
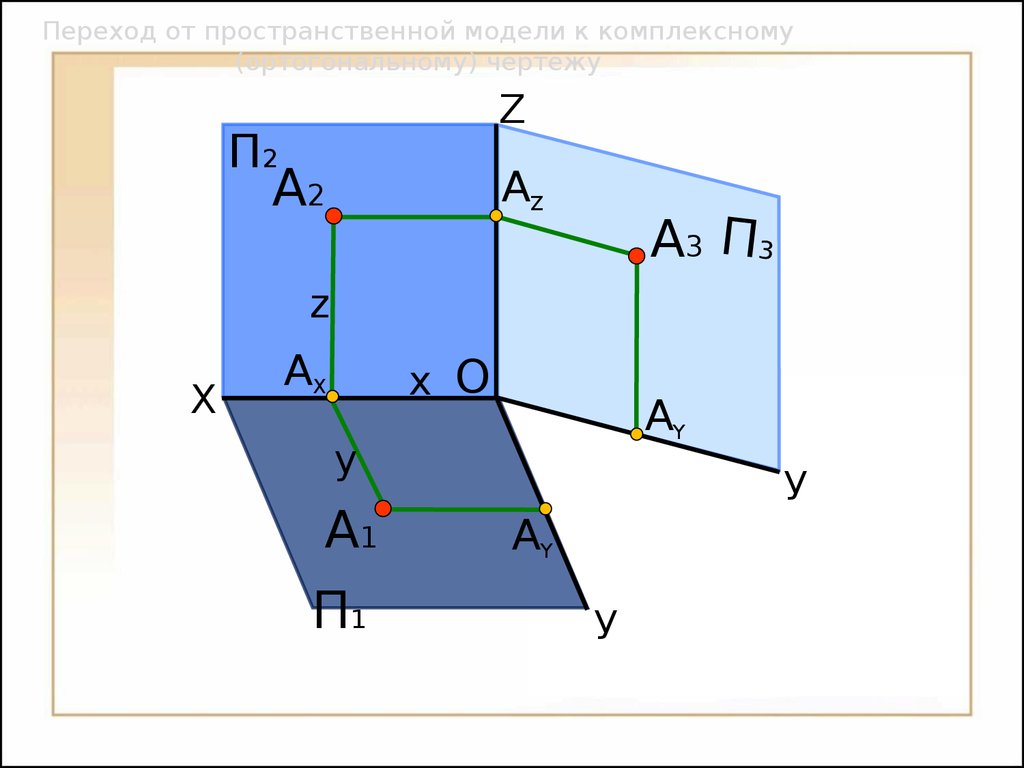
Октанты пространства ТочкаOП2П1П3XYZАXАYА1А2А3АZOXYZАXАYА1А2А3АZxyz25 ТочкаП2П1П3 Переход от пространственной модели к комплексному (ортогональному) чертежу26П2П1П3XZАXАYА1А2А3АZ Переход от пространственной модели к комплексному (ортогональному) чертежуOxyz27УАYА1А3 Переход от пространственной модели к комплексному (ортогональному) чертежуАYП1П3XУАZП2ZА2АXOxyz28 Переход от пространственной модели к комплексному (ортогональному) чертежуП1П3XУOАYА1А3АYАXАZП2ZА2xyz29 Переход от пространственной модели к комплексному (ортогональному) чертежуП1П3XУАYА1А3АYАXАZП2ZА2xyz30O Переход от пространственной модели к комплексному (ортогональному) чертежуXУП1П3АYА1А3АYАXАZП2ZА2xyz31O Переход от пространственной модели к комплексному (ортогональному) чертежуXУП1П3АYА1А3АYАXАZП2ZА2xyz32O Переход от пространственной модели к комплексному (ортогональному) чертежуXУАYА1АYАXАZП2ZА2П1П3А3xyz33O 1.
Положение точки в пространстве определяется тремя координатами A(x, y, z);
2.
Положение проекции точки на плоскости проекций определяется двумя координатамиА1 (x, y), А2 (x, z), А3 (y, z);
3.
Две проекции точки определяют ее положение в пространстве;
4.
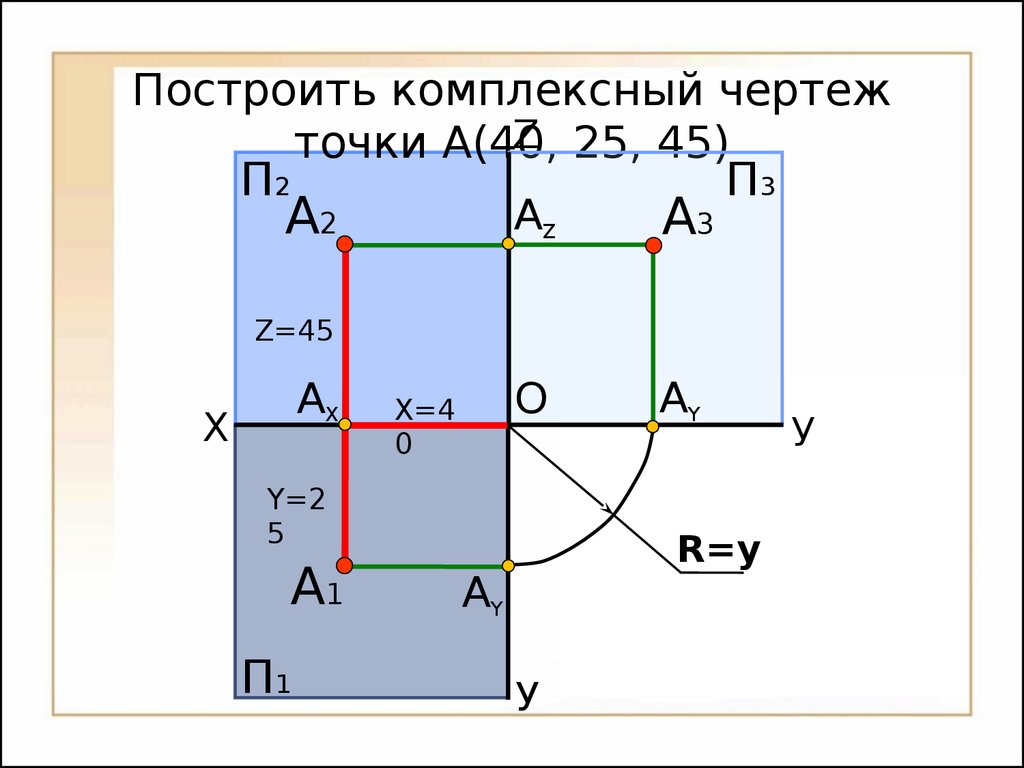
Две проекции точки лежат на линии связи, перпендикулярной координатной оси.34 Построить комплексный чертеж точки А(40, 25, 45)XУАYА1АYАXАZП2ZА2П1П3А3 X=40Y=25 Z=4535O Построить комплексный чертеж точки А(40, 25, 45)XУАYА1АYАXАZOП2ZА2П1П3А3X=40Y=25 Z=45R=y36 Линия– это множество всех последовательных положений двигающейся точки.
Прямая линия – линия, образованная движением точки не меняющей своего направления.
Прямая линия Прямая линия может быть задана: 1.
Двумя точками ей принадлежащими 2.
Одной точкой и направлением линии37 Прямая линия не параллельная и не перпендикулярная ни одной из плоскостей проекций называется – прямой общего положения.
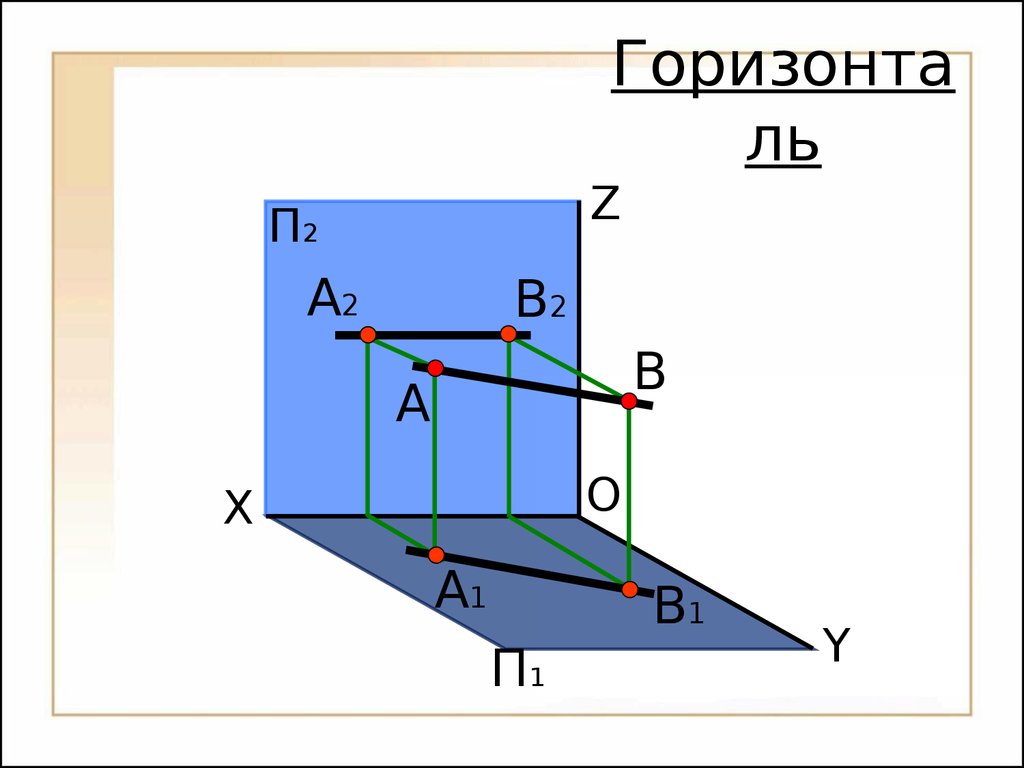
Прямая линия общего положения Замечание: На комплексном чертеже проекции прямой общего положения не параллельны и не перпендикулярны ни одной координатной оси.38OП2П1XYZА1А2 Прямая линия общего положенияВ1В239XУУА1OП2ZА2П1П3А3 Комплексный чертеж прямой линии общего положенияВ1В2В340 Проецирующие прямые Прямые уровня Прямые частные положения Прямые параллельные или перпендикулярные плоскостям проекций Прямые параллельные или перпендикулярные плоскостям проекций параллельные плоскостям проекций параллельные плоскостям проекций параллельна П1 параллельна П3 перпендикулярные плоскостям проекций перпендикулярные плоскостям проекций перпендикулярная П3 перпендикулярная П2 перпендикулярная П1 Профильно- проецирующая прямая Фронтально- проецирующая прямая Горизонтально- проецирующая прямая Профильная прямая Фронталь Горизонталь Прямые линии частного положения параллельнаП241OП2П1XYZА1А2 Горизонта льВ1В242XУА1OП2ZА2П1П3А3 Комплексный чертеж горизонталиВ1В2В3 Н.В.β - угол наклона прямой к плоскости проекций П2;β - угол наклона прямой к плоскости проекций П3. Свойства горизонтали: 1.
Горизонтальная проекция горизонтали А1В1 – натуральная величина;У 2.
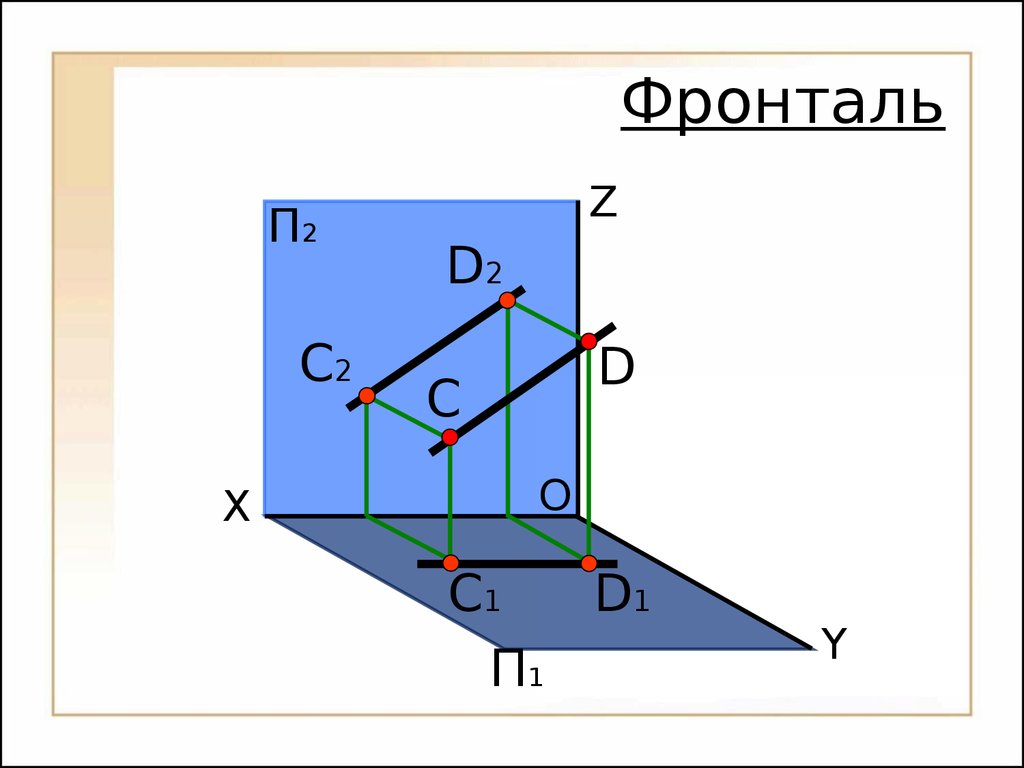
Фронтальная проекция горизонтали А2В2 параллельна оси ОХ.43OП2П1XYZC1CС2 ФронтальD1D244XУC1OП2ZС2П1П3C3 Комплексный чертеж фронталиD1D2D3 Н.В. - угол наклона прямой к плоскости проекций П3. Свойства фронтали: 1.
Фронтальная проекция фронтали C2D2 – натуральная величина;У 2.
Горизонтальная проекция фронтали C1D1 параллельна оси ОХ. - угол наклона прямой к плоскости проекций П1;45 Свойства проекций прямых уровня Если прямая параллельна плоскости проекций, то: на эту плоскость проецируются в натуральную величину сама прямая и углы наклона ее к двум другим плоскостям проекций;
проекции прямой на две другие плоскости проекций, параллельны координатным осям.46OП2П1XYZА2А1=В1В2 Горизонтально- проецирующая прямая Свойства горизонтально- проецирующей прямой: (АВ) П1;
(АВ) // П2;
(АВ) // П3.
Свойства ее проекций: 1.
Горизонтальная проекция А1В1 – точка;
2.
|А2В2 |=|А3В3 |=|АВ|;
3.
(А2В2) OX;
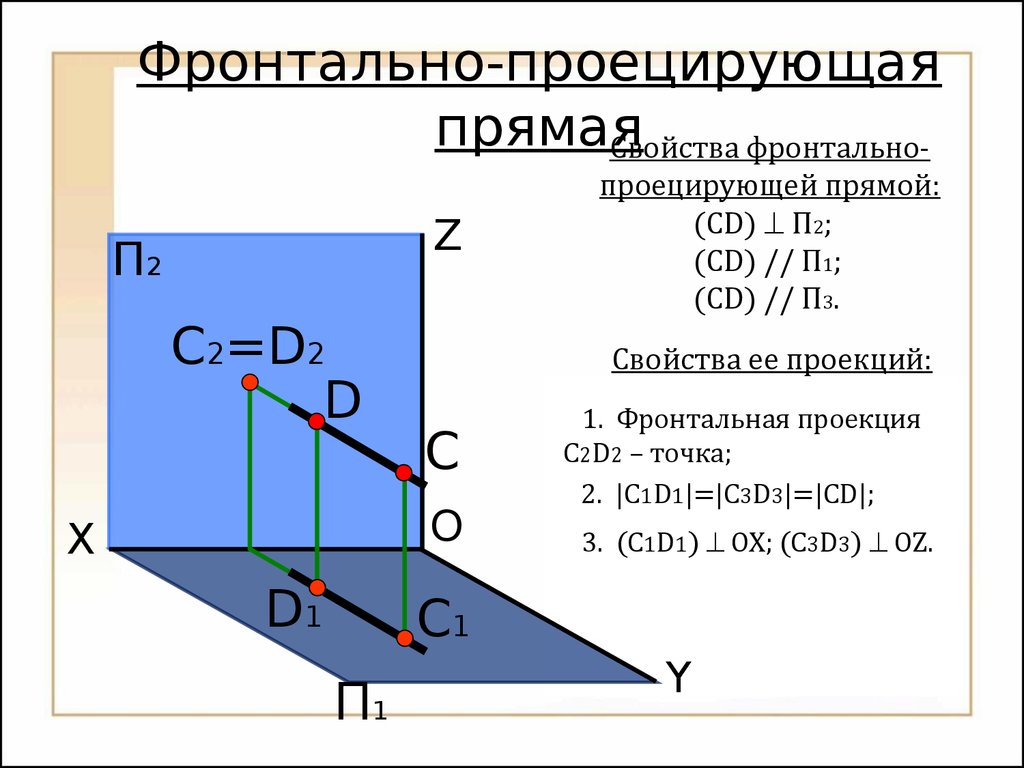
(А3В3)OY.47OП2П1XYZС1DС2=D2 Фронтально-проецирующая прямая Свойства фронтально- проецирующей прямой: (CD) П2;
(CD) // П1;
(CD) // П3.
Свойства ее проекций: 1.
Фронтальная проекция С2D2 – точка;
2.
|C1D1 |=|C3D3 |=|CD|;
3.
(C1D1) OX;
(C3D3)OZ.D148 Свойства проекций проецирующих прямых Если прямая перпендикулярна плоскости проекций, то: на эту плоскость она проецируются в точку;
проекции прямой на две другие плоскости проекций проецируются в натуральную величину и перпендикулярны координатным осям.4950 доценты кафедры «Начертательная геометрия, инженерная и компьютерная графика» Омского Государственного технического университета: Авторы: Бондарев Олег Александрович, к.т.н., Кайгородцева Наталья Викторовна, к.пед.н.
Точка.
Прямая.
Лекция № 1 План лекции Введ ение12 Историческая справка3 Методы проецирования4 Точка5 Прямая линия Инженерная графика (Черчение) Начертательная геометрия.
Введ ение Входят в список дисциплин, составляющих основу инженерного образования.
Начертательная геометрия- наука о проекционных изображениях.
Предметом начертательной геометрии являются:
• Способы построения изображений пространственных форм на плоскости;
• Исследование геометрических свойств объектов по их изображениям.5 В инженерной графике изучают: методы изображения предметов;
правила выполнения и чтения чертежей деталей и сборочных единиц.
Литература Ляшков А.А., Куликов Л.К., Панчук К.Л.
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ (конспект лекций) Омск: Изд-во ОмГТУ, 2005
• Гордон В.О., Семенцов – Огиевский М.А.
Курс начертательной геометрии: учебник.
– М.: Высшая школа, 2007.
• Бубенников А.В.
Начертательная геометрия: учебник.
– М.: Высш.
шк., 1985.
• Фролов С.А.
Начертательная геометрия: учебник.
– М.: ИНФРА–М, 2007.
Историческая справка С древних времён человек старался сохранить образ увиденного.
Наскальная живопись, украшенные рисунками стены жилища, посуда, предметы быта – первые тому свидетельства.
Цивилизация развивалась, появились схемы и карты местности, изображение храмовых комплексов, жилых домов, военных сооружений, мостов, простых механизмов.
Потребовалась выработка и первых общих правил представления пространственной информации на плоскости.
Семь чудес света трудно представить без первых чертежей, рисунков и схем.
Египетские, греческие и римские учёные, изучая перспективу, пытались выработать некие правила представления имеющейся информации.
Эпоха Возрождения вызвала расцвет архитектуры, скульптуры, живописи.
Первые теоретические основы перспективы создал итальянский учёный Историческая справка Леон Баттиста Альберти (1404 -1472) Дополнил линейную перспективу учением "Об уменьшении цветов и отчётливости очертаний".
Историческая справка Леонардо да Винчи (1452 -1519) Ввел метод координат французский архитектор Историческая справка Жерар Дезарг (1593 -1662) 1795 г.
- появилась "Начертательная геометрия" Гаспара Монжа, им введено понятие «комплексный чертёж» и получены полностью обратимые изображения объемных (пространственных) объектов на плоскости.
Историческая справка Гаспар Монж (1746 -1818) Основоположник начертательной геометрии - Первый учебник по начертательной геометрии опубликован во Франции в 1798 г.
Россия .
Развитию начертательной геометрии способствовали А.
Рублёв, Дионисий, архитекторы В.Баженов, А.Ворончихин;
самоучки, механики- изобретатели И.
Ползунов, И.
Кулибин, И.
Моторин и другие.
1810 г.
– Карл Потье читает в С.-Петербурге первые лекции в Институте корпуса инженеров путей сообщения.
1821 г.
– Я.А.
Севастьянов (1796-1849) издает оригинальный курс начертательной геометрии на русском языке.
Историческая справка 1900 г.
– в Сибири, в Томском техническом институте курс начертательной геометрии прочитан Историческая справка Позже в России начертательная геометрия развивалась трудами Н.
Макарова, В.
Курдюмова, А.
Власова, Н.
Глаголева, Н.
Четверухина и многих других.
Валентином Николаевичем Джонсом 28(16)октября 1900г.
Методы проециро вания Методы проециро вания ЦЕНТРАЛЬНОЕ ПАРАЛЛЕЛЬНОЕП1А1В1С1ACBS Центральное проецированиеП1А1В1С1ACBSП1А1В1С1AC Параллельное проецированиеB º- прямоугольное проецирование ≠ º- косоугольное проецированиеs Достижение обратимости комплексного чертежа дополнениями П’ M’ N’MsM1N1M2N2M3N3 Числовые отметкиА6AП1BCB-4=C0 Векторы ФедороваП1А1В1АВ90 Вторая плоскость (метод Монжа)XП2П1А1А2 VIIIVIIVI-УXП1П2П3-XУZ-ZIIIOIVVIII Модель основных плоскостей проекций.
Октанты пространства ТочкаOП2П1П3XYZАXАYА1А2А3АZOXYZАXАYА1А2А3АZxyz25 ТочкаП2П1П3 Переход от пространственной модели к комплексному (ортогональному) чертежу26П2П1П3XZАXАYА1А2А3АZ Переход от пространственной модели к комплексному (ортогональному) чертежуOxyz27УАYА1А3 Переход от пространственной модели к комплексному (ортогональному) чертежуАYП1П3XУАZП2ZА2АXOxyz28 Переход от пространственной модели к комплексному (ортогональному) чертежуП1П3XУOАYА1А3АYАXАZП2ZА2xyz29 Переход от пространственной модели к комплексному (ортогональному) чертежуП1П3XУАYА1А3АYАXАZП2ZА2xyz30O Переход от пространственной модели к комплексному (ортогональному) чертежуXУП1П3АYА1А3АYАXАZП2ZА2xyz31O Переход от пространственной модели к комплексному (ортогональному) чертежуXУП1П3АYА1А3АYАXАZП2ZА2xyz32O Переход от пространственной модели к комплексному (ортогональному) чертежуXУАYА1АYАXАZП2ZА2П1П3А3xyz33O 1.
Положение точки в пространстве определяется тремя координатами A(x, y, z);
2.
Положение проекции точки на плоскости проекций определяется двумя координатамиА1 (x, y), А2 (x, z), А3 (y, z);
3.
Две проекции точки определяют ее положение в пространстве;
4.
Две проекции точки лежат на линии связи, перпендикулярной координатной оси.34 Построить комплексный чертеж точки А(40, 25, 45)XУАYА1АYАXАZП2ZА2П1П3А3 X=40Y=25 Z=4535O Построить комплексный чертеж точки А(40, 25, 45)XУАYА1АYАXАZOП2ZА2П1П3А3X=40Y=25 Z=45R=y36 Линия– это множество всех последовательных положений двигающейся точки.
Прямая линия – линия, образованная движением точки не меняющей своего направления.
Прямая линия Прямая линия может быть задана: 1.
Двумя точками ей принадлежащими 2.
Одной точкой и направлением линии37 Прямая линия не параллельная и не перпендикулярная ни одной из плоскостей проекций называется – прямой общего положения.
Прямая линия общего положения Замечание: На комплексном чертеже проекции прямой общего положения не параллельны и не перпендикулярны ни одной координатной оси.38OП2П1XYZА1А2 Прямая линия общего положенияВ1В239XУУА1OП2ZА2П1П3А3 Комплексный чертеж прямой линии общего положенияВ1В2В340 Проецирующие прямые Прямые уровня Прямые частные положения Прямые параллельные или перпендикулярные плоскостям проекций Прямые параллельные или перпендикулярные плоскостям проекций параллельные плоскостям проекций параллельные плоскостям проекций параллельна П1 параллельна П3 перпендикулярные плоскостям проекций перпендикулярные плоскостям проекций перпендикулярная П3 перпендикулярная П2 перпендикулярная П1 Профильно- проецирующая прямая Фронтально- проецирующая прямая Горизонтально- проецирующая прямая Профильная прямая Фронталь Горизонталь Прямые линии частного положения параллельнаП241OП2П1XYZА1А2 Горизонта льВ1В242XУА1OП2ZА2П1П3А3 Комплексный чертеж горизонталиВ1В2В3 Н.В.β - угол наклона прямой к плоскости проекций П2;β - угол наклона прямой к плоскости проекций П3. Свойства горизонтали: 1.
Горизонтальная проекция горизонтали А1В1 – натуральная величина;У 2.
Фронтальная проекция горизонтали А2В2 параллельна оси ОХ.43OП2П1XYZC1CС2 ФронтальD1D244XУC1OП2ZС2П1П3C3 Комплексный чертеж фронталиD1D2D3 Н.В. - угол наклона прямой к плоскости проекций П3. Свойства фронтали: 1.
Фронтальная проекция фронтали C2D2 – натуральная величина;У 2.
Горизонтальная проекция фронтали C1D1 параллельна оси ОХ. - угол наклона прямой к плоскости проекций П1;45 Свойства проекций прямых уровня Если прямая параллельна плоскости проекций, то: на эту плоскость проецируются в натуральную величину сама прямая и углы наклона ее к двум другим плоскостям проекций;
проекции прямой на две другие плоскости проекций, параллельны координатным осям.46OП2П1XYZА2А1=В1В2 Горизонтально- проецирующая прямая Свойства горизонтально- проецирующей прямой: (АВ) П1;
(АВ) // П2;
(АВ) // П3.
Свойства ее проекций: 1.
Горизонтальная проекция А1В1 – точка;
2.
|А2В2 |=|А3В3 |=|АВ|;
3.
(А2В2) OX;
(А3В3)OY.47OП2П1XYZС1DС2=D2 Фронтально-проецирующая прямая Свойства фронтально- проецирующей прямой: (CD) П2;
(CD) // П1;
(CD) // П3.
Свойства ее проекций: 1.
Фронтальная проекция С2D2 – точка;
2.
|C1D1 |=|C3D3 |=|CD|;
3.
(C1D1) OX;
(C3D3)OZ.D148 Свойства проекций проецирующих прямых Если прямая перпендикулярна плоскости проекций, то: на эту плоскость она проецируются в точку;
проекции прямой на две другие плоскости проекций проецируются в натуральную величину и перпендикулярны координатным осям.4950 доценты кафедры «Начертательная геометрия, инженерная и компьютерная графика» Омского Государственного технического университета: Авторы: Бондарев Олег Александрович, к.т.н., Кайгородцева Наталья Викторовна, к.пед.н.






































 Инженерная графика
Инженерная графика








