Похожие презентации:
Основные задачи начертательной геометрии
1. Начертательная геометрия
2. Литература
1. Чекмарев А.А. Инженерная графика.- М.: Высшая школа, 1998
2. Нартова Л.Г. Начертательная
геометрия. - М.: Дрофа, 2003
3. Гордон В.О. Курс начертательной
геометрии. - М.: Высшая школа, 2003
3.
Основные задачи начертательной геометрии1.
Создание плоской геометрической
модели пространственного объекта –
чертежа (эпюра).
Эпюр – в переводе с греческого –
чертеж или проект.
2.
Решение задач на плоскости.
3.
Чтение чертежа (эпюра).
4.
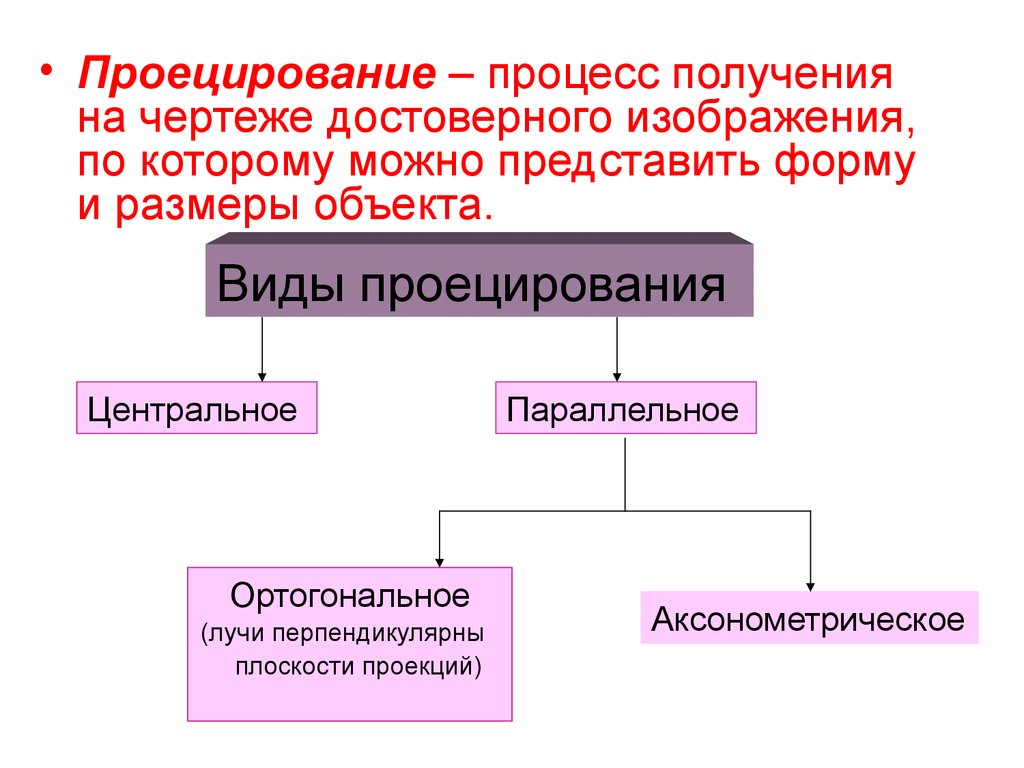
• Проецирование – процесс полученияна чертеже достоверного изображения,
по которому можно представить форму
и размеры объекта.
Виды проецирования
Центральное
Ортогональное
(лучи перпендикулярны
плоскости проекций)
Параллельное
Аксонометрическое
5.
Проекция – геометрическая модель,полученная проецированием объекта
на плоскость или какую-либо другую
поверхность.
Проекция объекта представляет
собой совокупность проекций всех
его точек.
6.
Центральное проецированиеS – центр
проецирования;
S
C
В
П – плоскость проекций;
А
А, В, – точки
пространства;
Ап
Вп
Cп
П
SA, SB, –
проецирующие лучи;
Ап, Вп, Сп – проекции
точек на плоскости П.
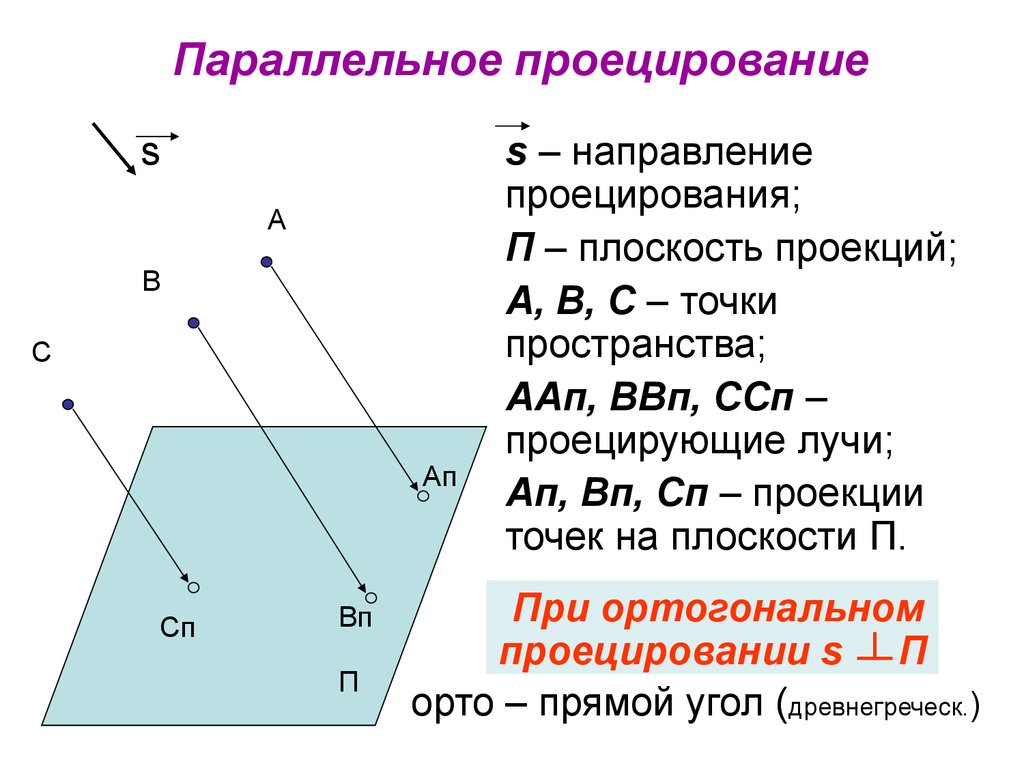
7. Параллельное проецирование
sА
В
С
Ап
Сп
Вп
П
s – направление
проецирования;
П – плоскость проекций;
А, В, С – точки
пространства;
ААп, ВВп, ССп –
проецирующие лучи;
Ап, Вп, Сп – проекции
точек на плоскости П.
При ортогональном
проецировании s П
орто – прямой угол (древнегреческ.)
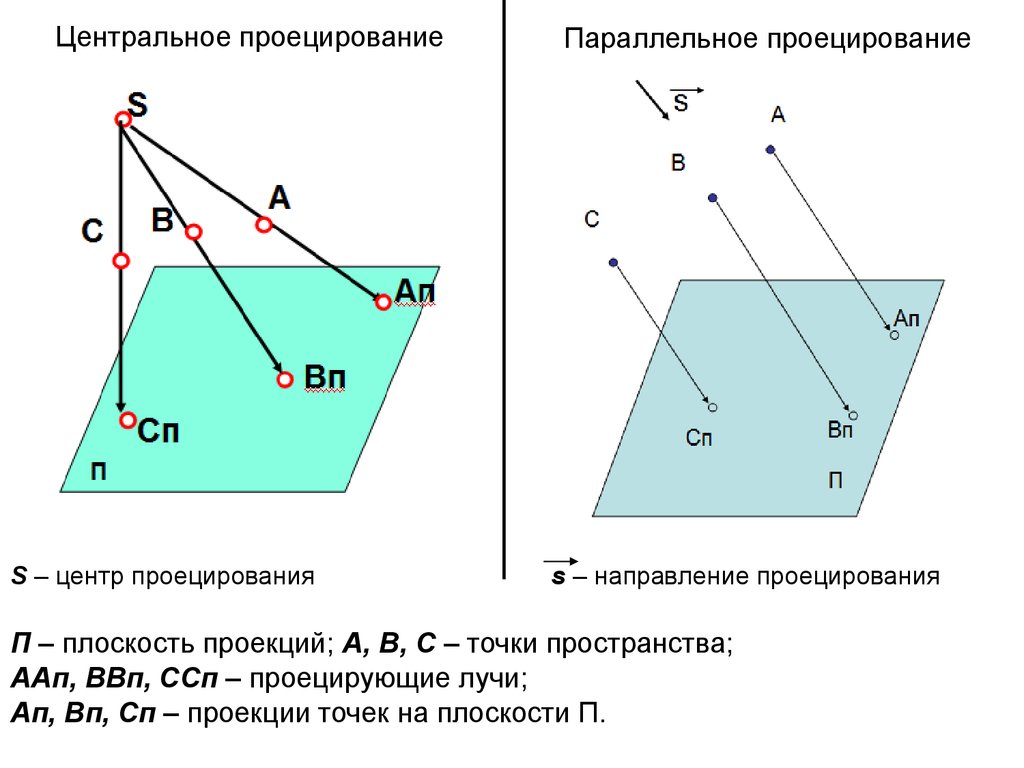
8. Центральное проецирование
S – центр проецированияПараллельное проецирование
s – направление проецирования
П – плоскость проекций; А, В, С – точки пространства;
ААп, ВВп, ССп – проецирующие лучи;
Ап, Вп, Сп – проекции точек на плоскости П.
9.
По одной проекции невозможнооднозначно определить положение
объекта в пространстве.
Для однозначного определения места
расположения объекта в пространстве
французский ученый Гаспар Монж
предложил проецировать объект на
три
взаимно
перпендикулярные
плоскости
10.
• Гаспар Монж (1746 – 1818) в1799 г. создал классический
труд по НГ, изданный в
Париже.
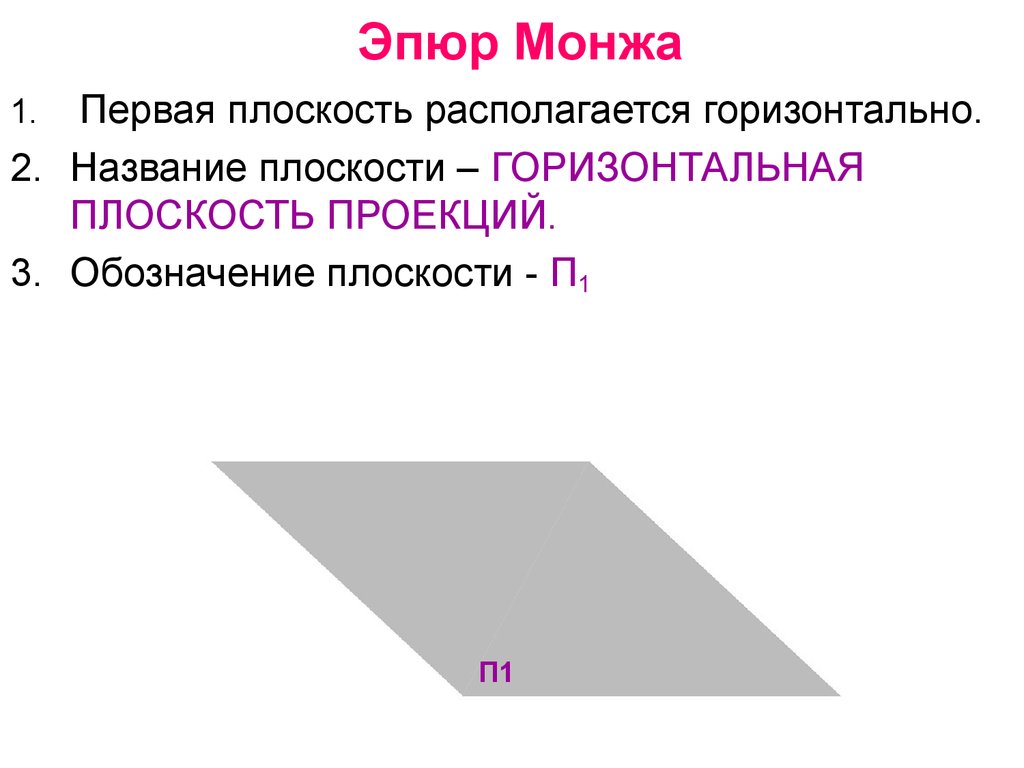
11. Эпюр Монжа
Первая плоскость располагается горизонтально.2. Название плоскости – ГОРИЗОНТАЛЬНАЯ
ПЛОСКОСТЬ ПРОЕКЦИЙ.
3. Обозначение плоскости - П1
1.
П1
12.
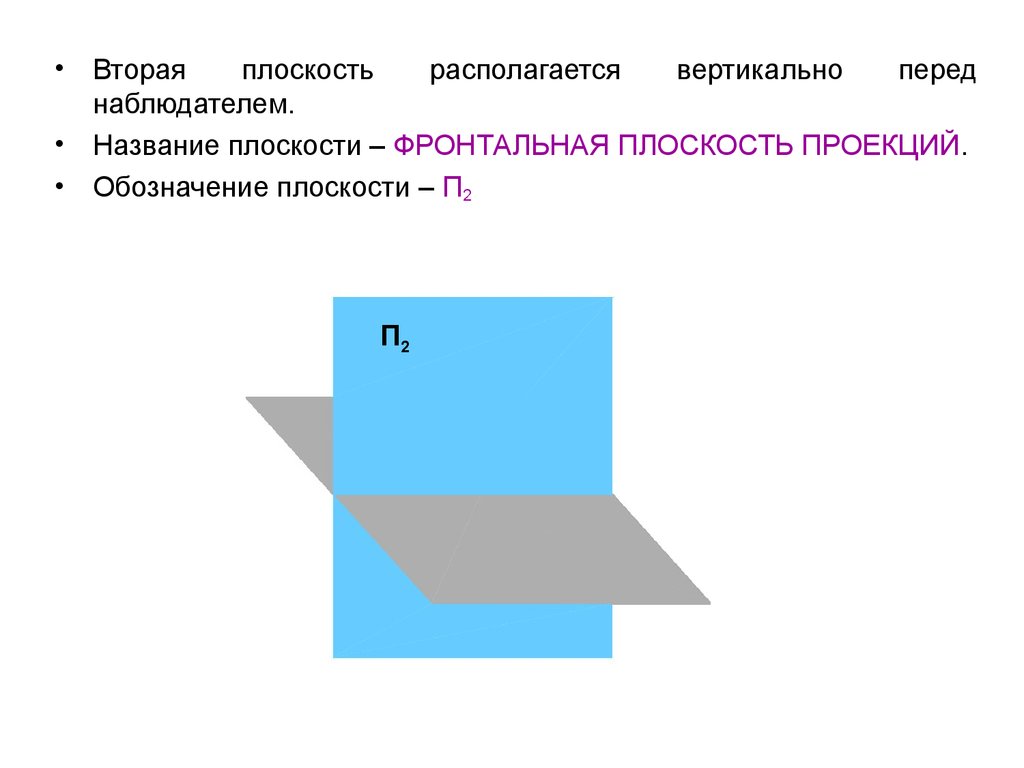
Вторая
плоскость
располагается
вертикально
перед
наблюдателем.
Название плоскости – ФРОНТАЛЬНАЯ ПЛОСКОСТЬ ПРОЕКЦИЙ.
Обозначение плоскости – П2
П2
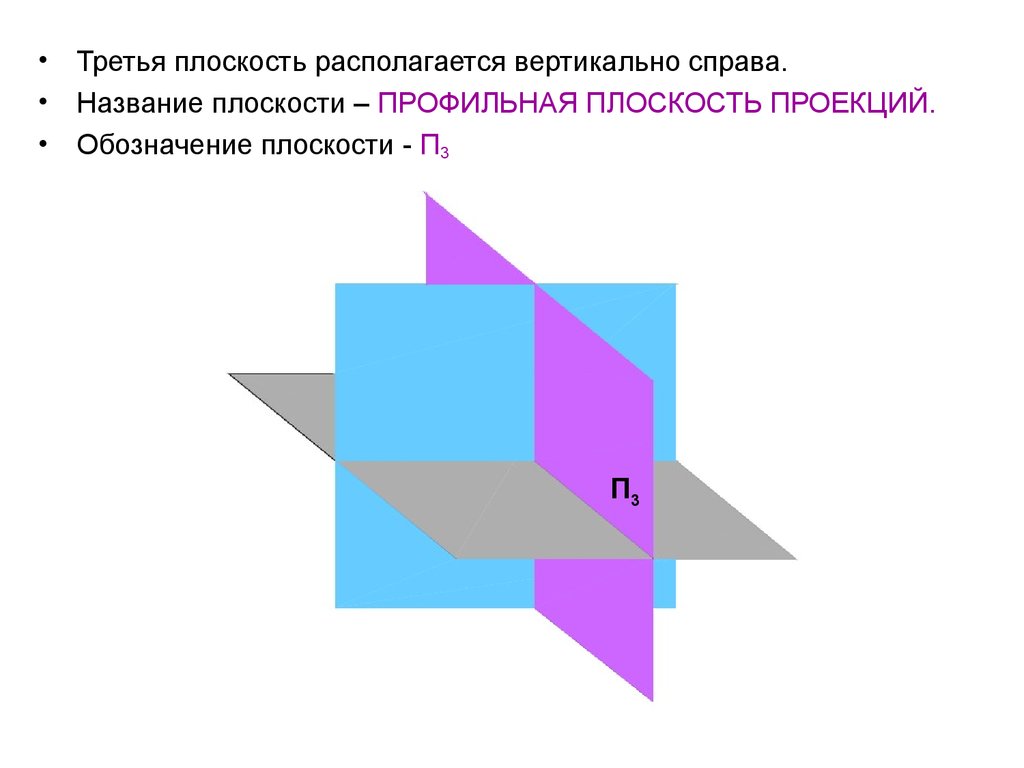
13.
• Третья плоскость располагается вертикально справа.• Название плоскости – ПРОФИЛЬНАЯ ПЛОСКОСТЬ ПРОЕКЦИЙ.
• Обозначение плоскости - П3
П3
14.
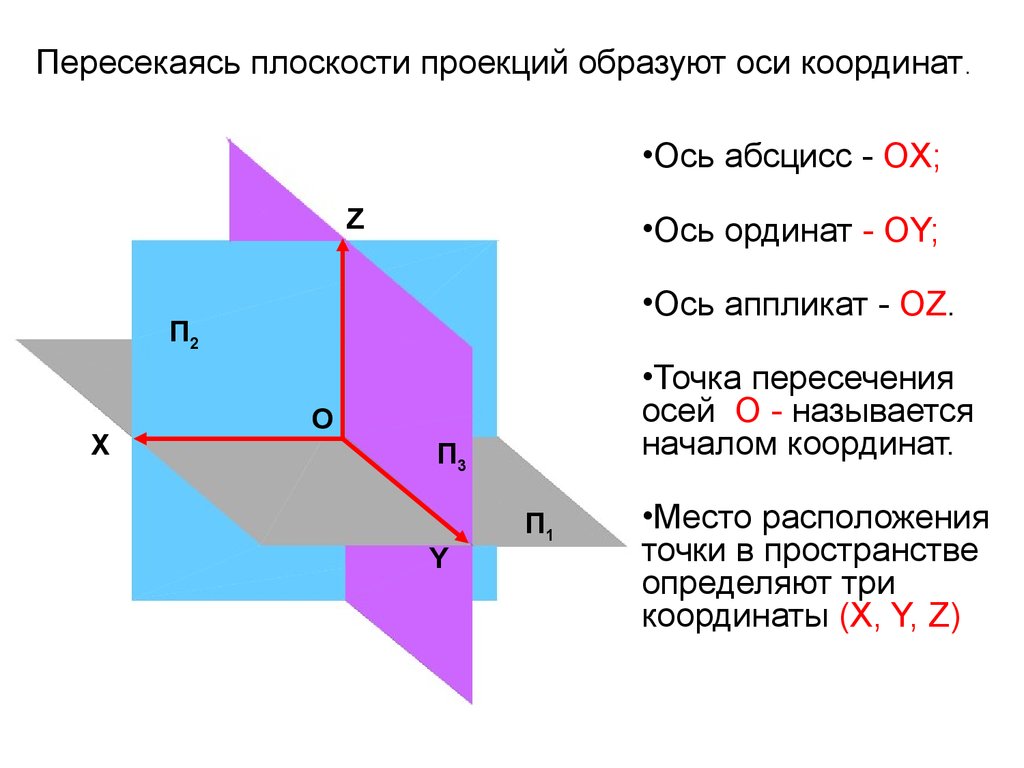
Пересекаясь плоскости проекций образуют оси координат.•Ось абсцисс - ОX;
Z
•Ось ординат - ОY;
•Ось аппликат - ОZ.
П2
X
•Точка пересечения
осей О - называется
началом координат.
О
П3
Y
П1
•Место расположения
точки в пространстве
определяют три
координаты (X, Y, Z)
15.
Введенные плоскости проекций разделяют пространство на восемьоктантов: І, ІІ, ІІІ, ІV, V,VІ, VІІ,VІІІ.
ІІ
VІ
Z
П2
І
ІІІ
X
V
О
П3
Y
ІV
П1
VІІ
І
16.
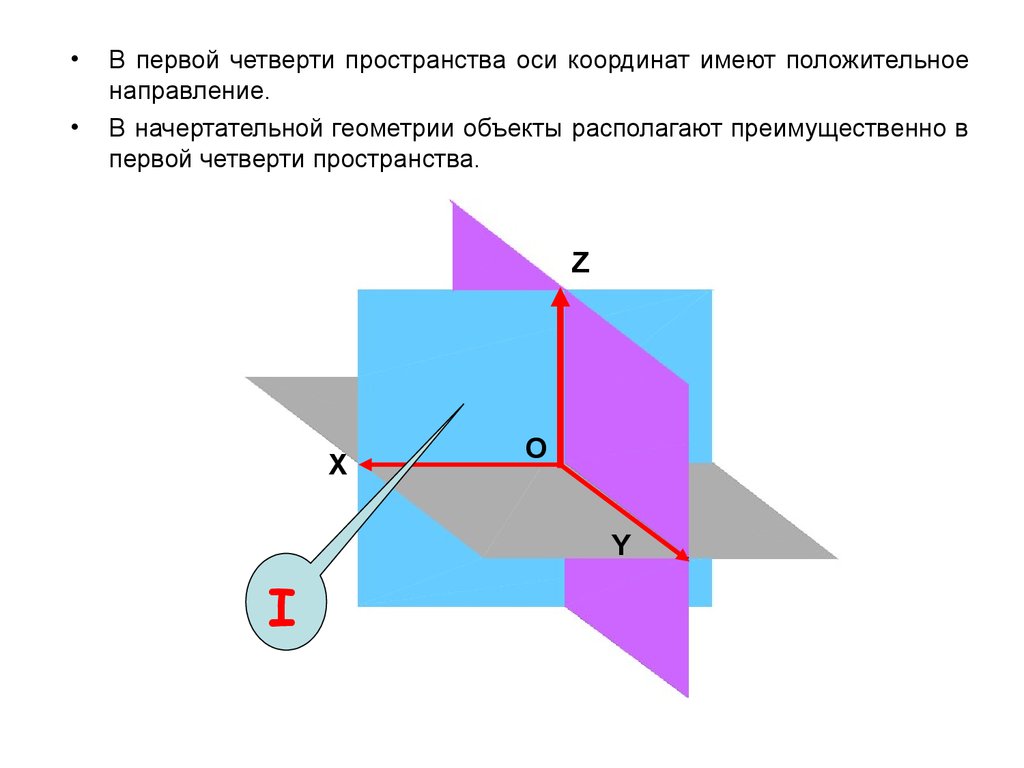
В первой четверти пространства оси координат имеют положительное
направление.
В начертательной геометрии объекты располагают преимущественно в
первой четверти пространства.
Z
X
O
Y
І
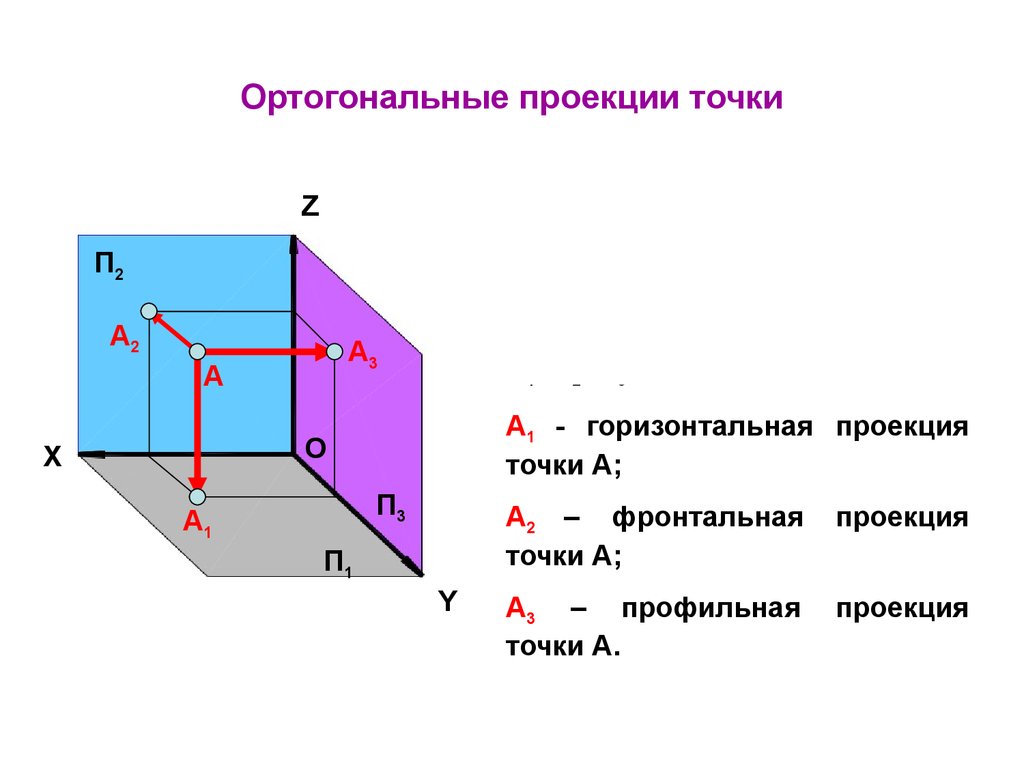
17. Ортогональные проекции точки
Возьмемв
пространстве
произвольную
точку
А
и
построим ее ортогональные
проекции на три взаимно
перпендикулярные плоскости
П1, П2, П3.
Z
П2
А2
А3
А
А1 - горизонтальная проекция
точки А;
O
X
П3
А1
П1
Y
А2 – фронтальная
точки А;
проекция
А3 – профильная
точки А.
проекция
18.
1. Расстояние ОАX – координата Xточки А (XA);
2. Расстояние AXА1 – координата Y
точки А (YA);
Z
П2
А2
X
А3
А
ZA
O
XA
Аx
YA
3. Расстояние A1А – координата Z
точки А (ZA).
Az
Аy
А1
П3
П1
Координата точки – это рассто-яние
от точки до плоскости (АА3, АА2,
АА1) или от оси координат до
проекции точки (AZA2,
A X A1,
AxA2).
Y
Координаты точки записывают так:
А(X, Y, Z)
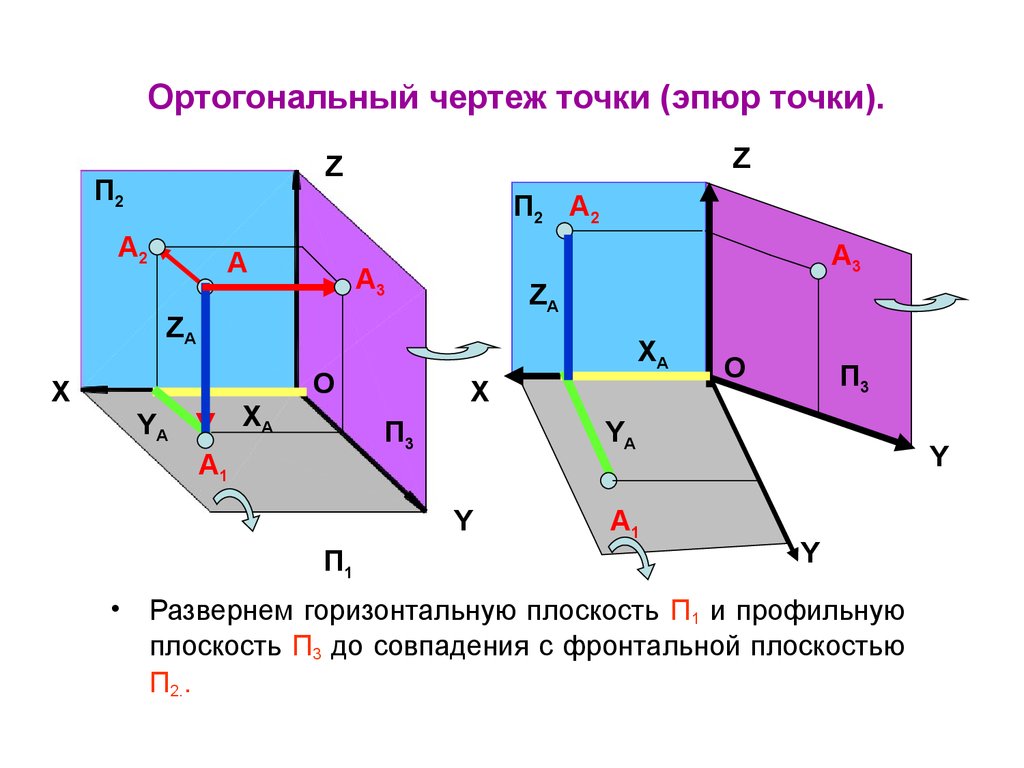
19. Ортогональный чертеж точки (эпюр точки).
ZZ
П2
П2 А 2
А2
А
А3
А3
ZA
ZA
XA
O
X
XA
YA
X
П3
А1
П3
YA
Y
П1
O
А1
Y
Y
Развернем горизонтальную плоскость П1 и профильную
плоскость П3 до совпадения с фронтальной плоскостью
П2..
20.
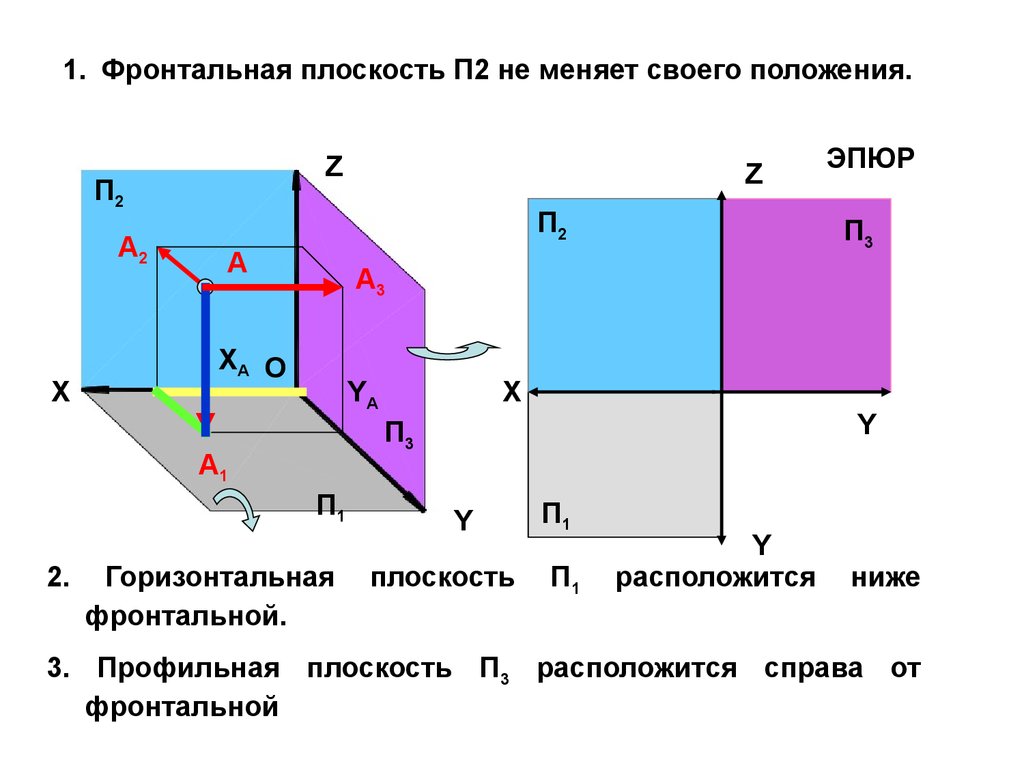
1. Фронтальная плоскость П2 не меняет своего положения.Z
П2
А2
X
П2
А
ЭПЮР
П3
А3
XA O
YA
X
Y
П3
А1
П1
2.
Z
Горизонтальная
фронтальной.
Y
плоскость
П1
П1
Y
расположится
ниже
3. Профильная плоскость П3 расположится справа от
фронтальной
21.
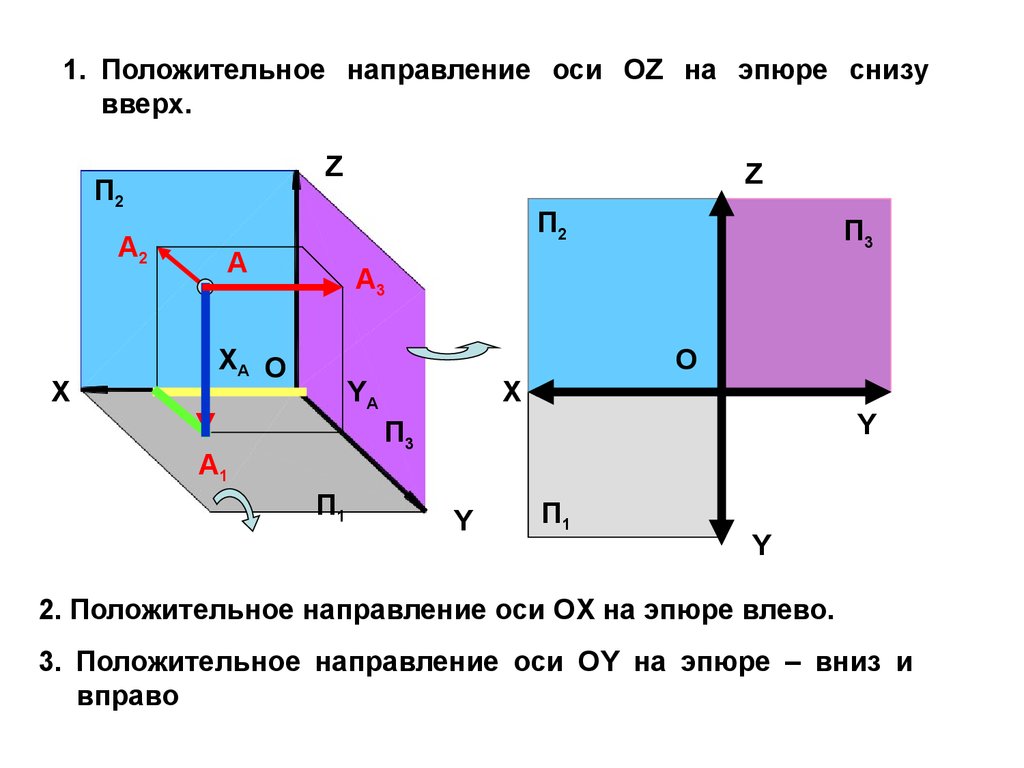
1. Положительное направление оси ОZ на эпюре снизувверх.
Z
П2
А2
X
Z
П2
А
П3
А3
XA O
O
YA
X
Y
П3
А1
П1
Y
П1
Y
2. Положительное направление оси ОX на эпюре влево.
3. Положительное направление оси ОY на эпюре – вниз и
вправо
22.
Откладываем последовательно, координаты точки А (XA,YA,ZA),в направлении осей координат.
Z
П2
Z
А2
А2
А
ZА
XA
X
YA
А3
ZA
O
XA
X
П3
А1
П1
Y
Y
YA
А1
Y
Откладываем координаты XA и YA. Построим горизонтальную
проекцию точки А → A1.
Откладываем координаты XA
проекцию точки А → А .
и ZА. Построим фронтальную
23.
ZП2
А2
X
Z
А2
А
XA O
А3
ZA
X
YA
Аx
П3
А1
Y
YA
Y
П1
XA
А1
Y
Сразу, по трем координатам строятся две проекции:
фронтальная и горизонтальная
24.
ZП2
А2
X
Z
А2
А
А3
XA O
А1
П1
А3
ZA
X
YA
XA
YA
АY
Y
YA
П3
АY
Y
А1
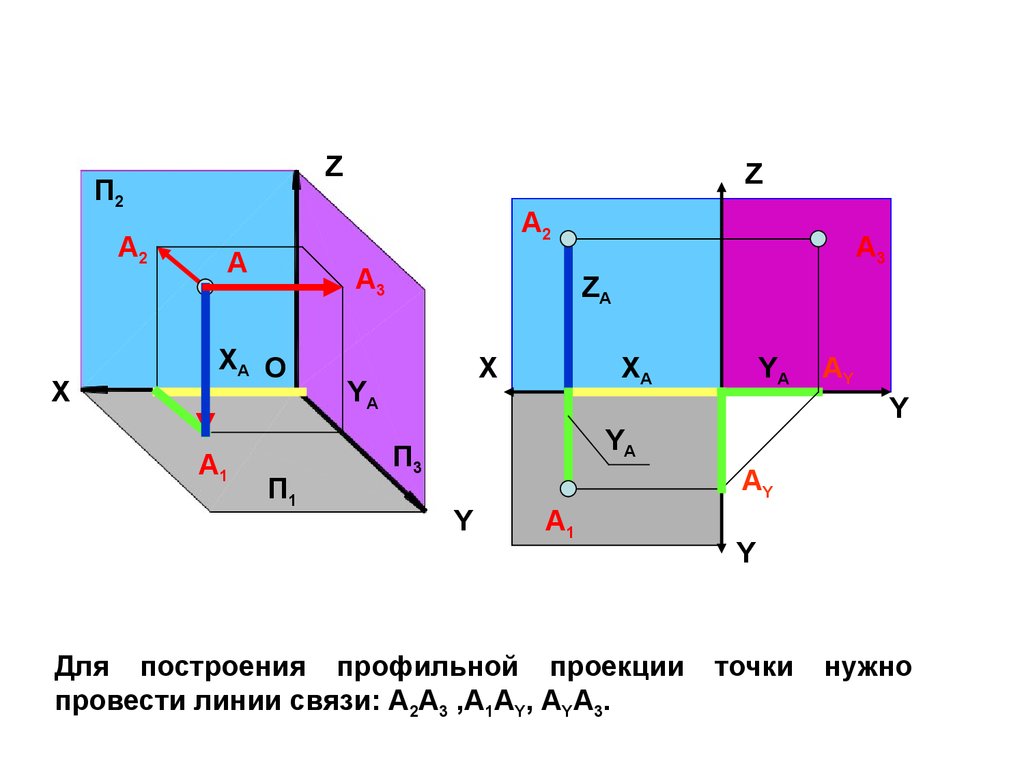
Для построения профильной проекции
провести линии связи: А2А3 ,A1АY, АYA3.
Y
точки
нужно
25.
ZП2
А2
X
Эпюр точки
Z
А2
А
А3
XA O
А1
П1
А3
ZA
XA
X
YA
YA
Y
YA
П3
АY
АY
Y
А1
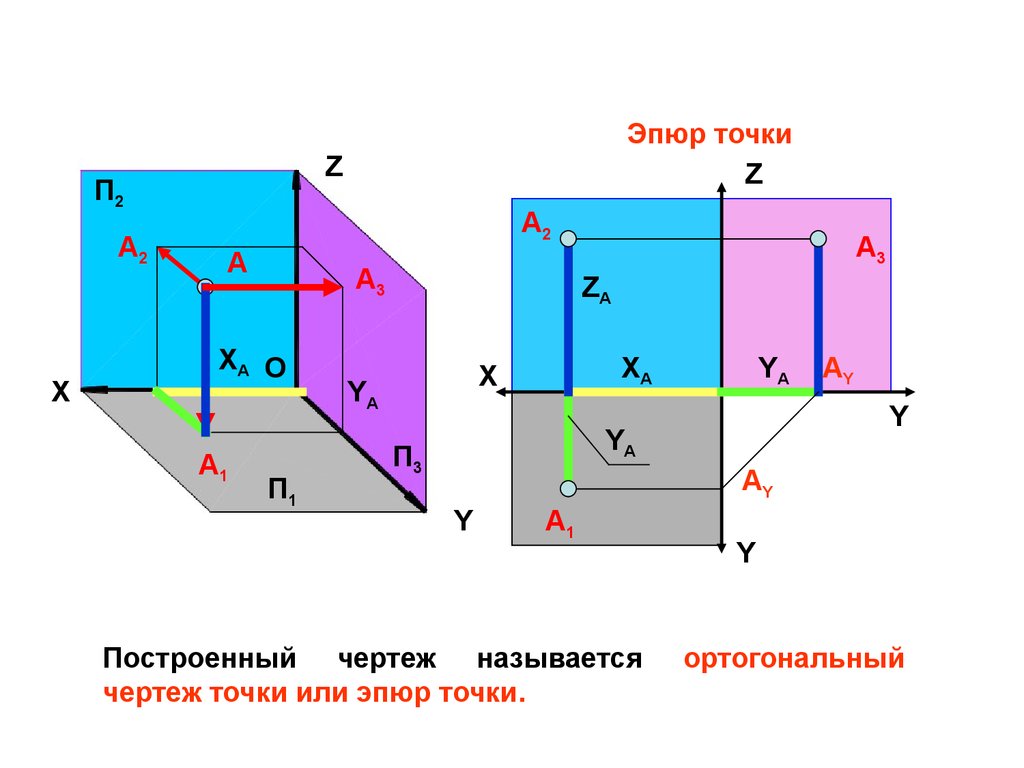
Построенный чертеж называется
чертеж точки или эпюр точки.
Y
ортогональный
26.
Ортогональный чертеж точки или эпюр точкиП1- горизонтальная плоскость проекций
ОХ- ось абсцисс
П2- фронтальная плоскость проекций
ОY- ось ординат
П3- профильная плоскость проекций
ОZ- ось аппликат
О –начало координат
27. Проекции отрезков прямой
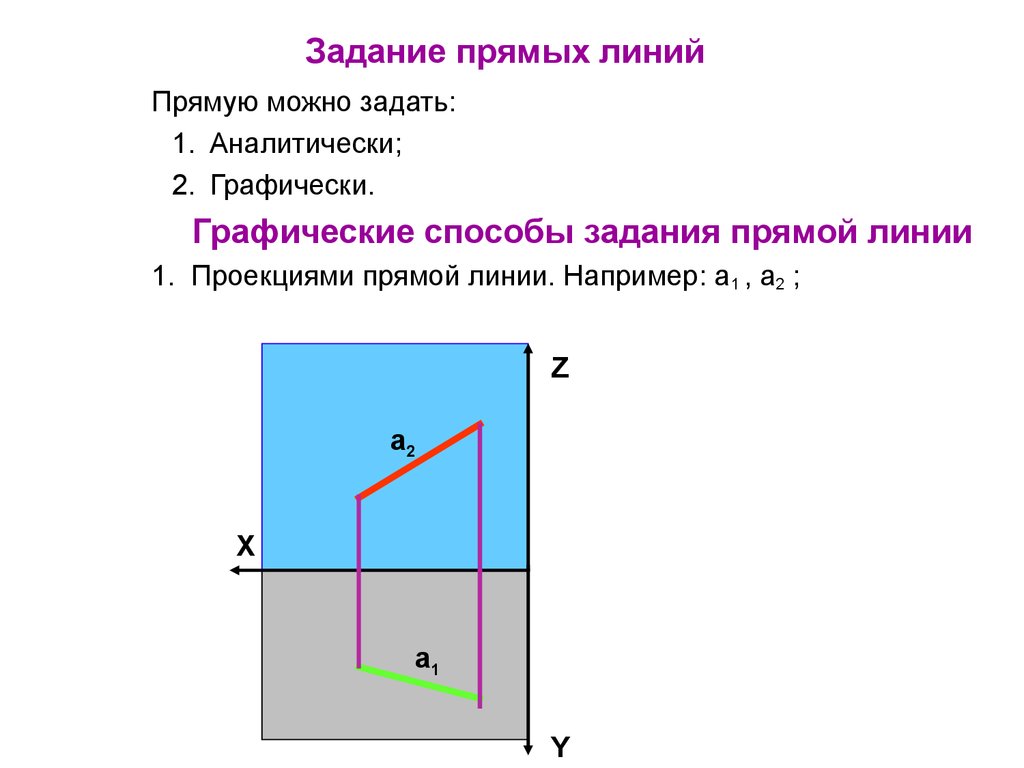
28. Задание прямых линий
Прямую можно задать:1. Аналитически;
2. Графически.
Графические способы задания прямой линии
1. Проекциями прямой линии. Например: а1 , а2 ;
Z
а2
X
а1
Y
29.
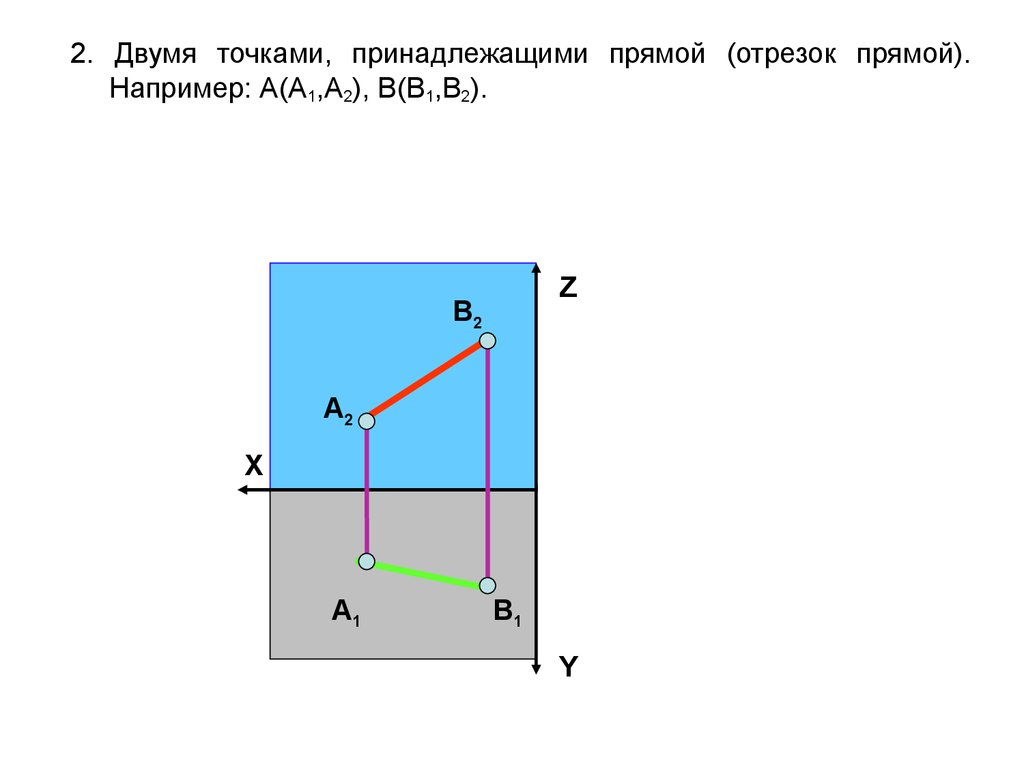
2. Двумя точками, принадлежащими прямой (отрезок прямой).Например: А(A1,A2), В(B1,B2).
Z
В2
А2
X
А1
В1
Y
30. Прямые общего и частного положения
Прямые общего положения - прямыене параллельные и не перпендикулярные
плоскостям проекций.
Прямые частного положения разделяют на:
1) Проецирующие прямые - прямые
перпендикулярные плоскостям проекций.
2) Линии уровня - прямые параллельные
плоскостям проекций.
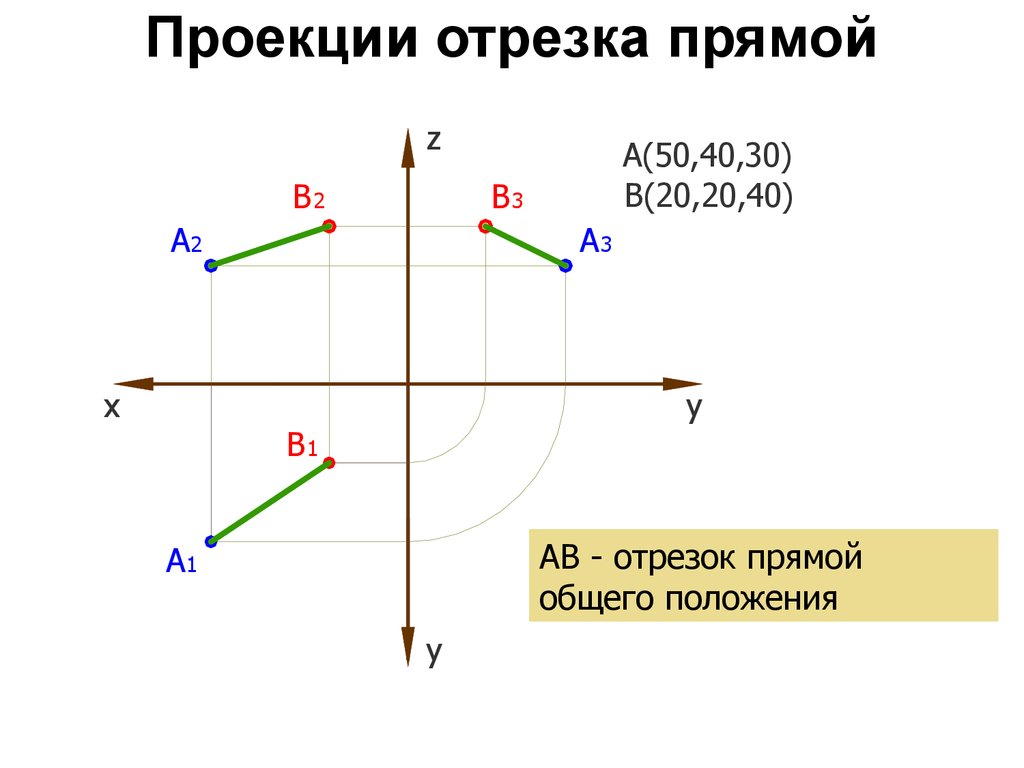
31. Проекции отрезка прямой
zB2
B3
A3
y = 40
y = 20
z = 30
z = 40
A2
x
y
B1
A1
A(50,40,30)
B(20,20,40)
АВ - отрезок прямой
общего положения
x=
x=
2050
y
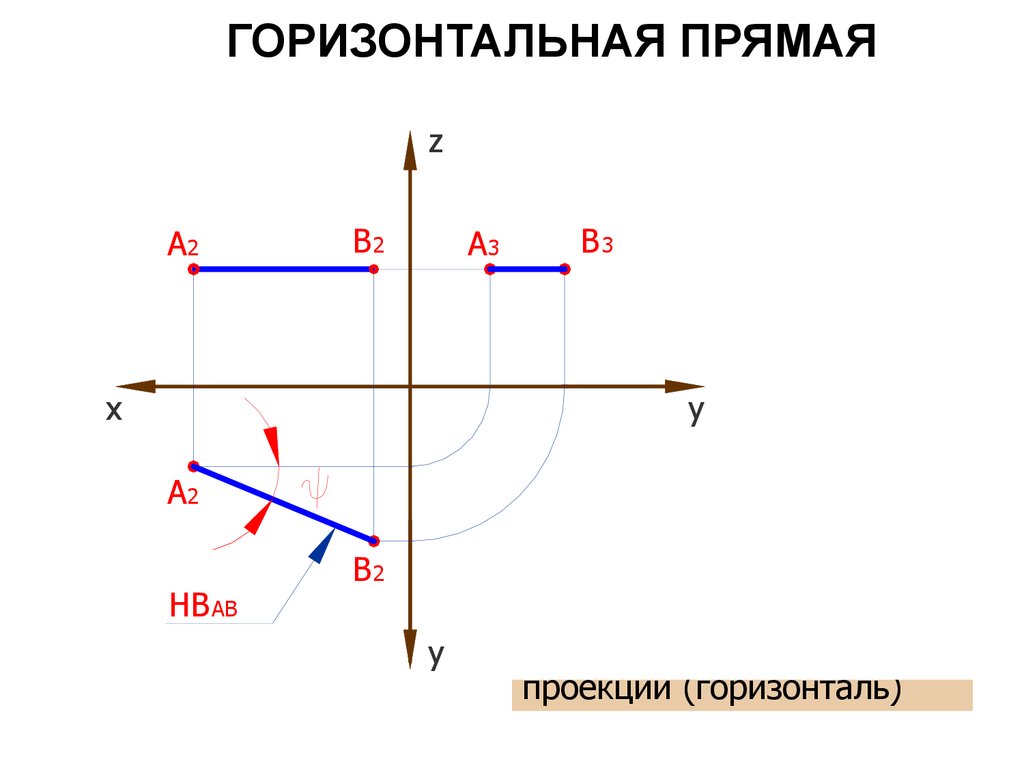
32. ГОРИЗОНТАЛЬНАЯ ПРЯМАЯ
zA2
B2
Z = const
A3
x
B3
y
A2
HB AB
B2
y
АВ параллельна
горизонтальной плоскости
проекций (горизонталь)
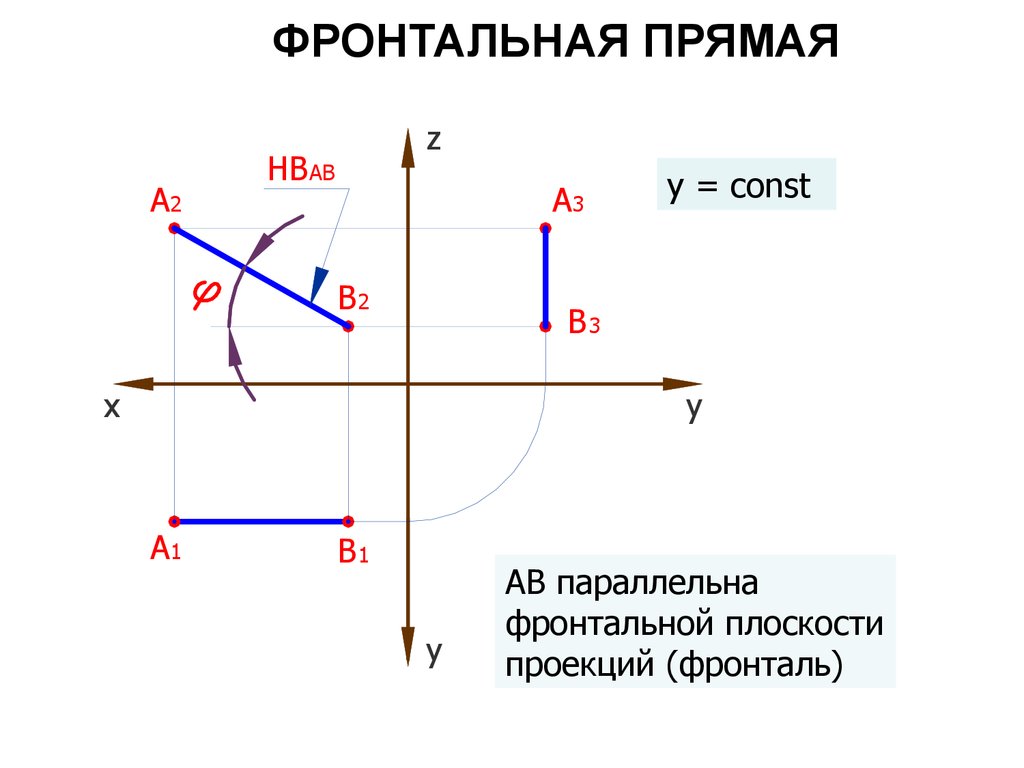
33. ФРОНТАЛЬНАЯ ПРЯМАЯ
A2z
HB AB
A3
B2
y = const
B3
x
y
A1
B1
y
АВ параллельна
фронтальной плоскости
проекций (фронталь)
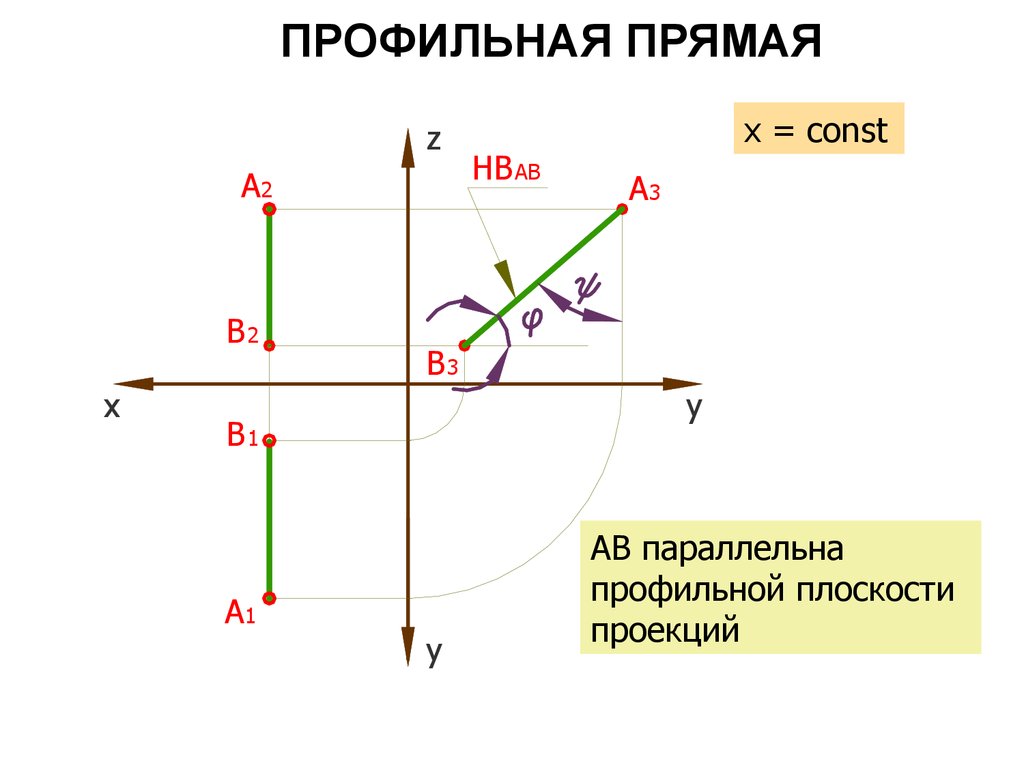
34. ПРОФИЛЬНАЯ ПРЯМАЯ
zA2
B2
x
A3
B3
y
B1
A1
HB AB
x = const
y
АВ параллельна
профильной плоскости
проекций
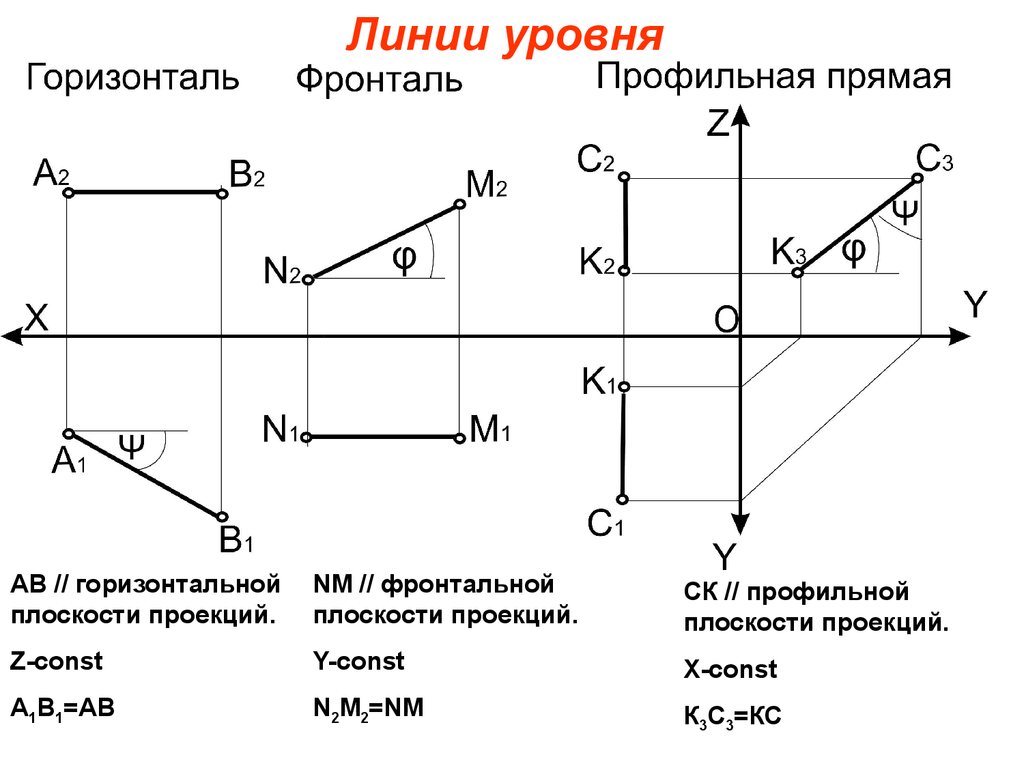
35. Линии уровня
АВ // горизонтальнойплоскости проекций.
NM // фронтальной
плоскости проекций.
СК // профильной
плоскости проекций.
Z-const
Y-const
X-const
А1В1=АВ
N2M2=NM
К3С3=КС
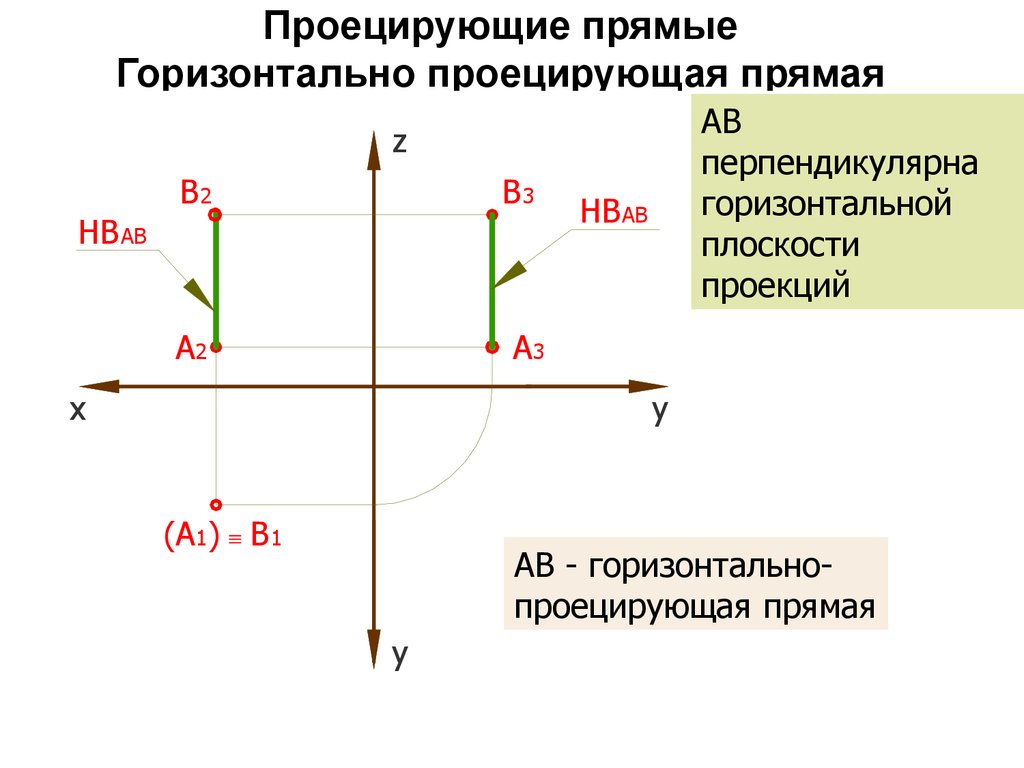
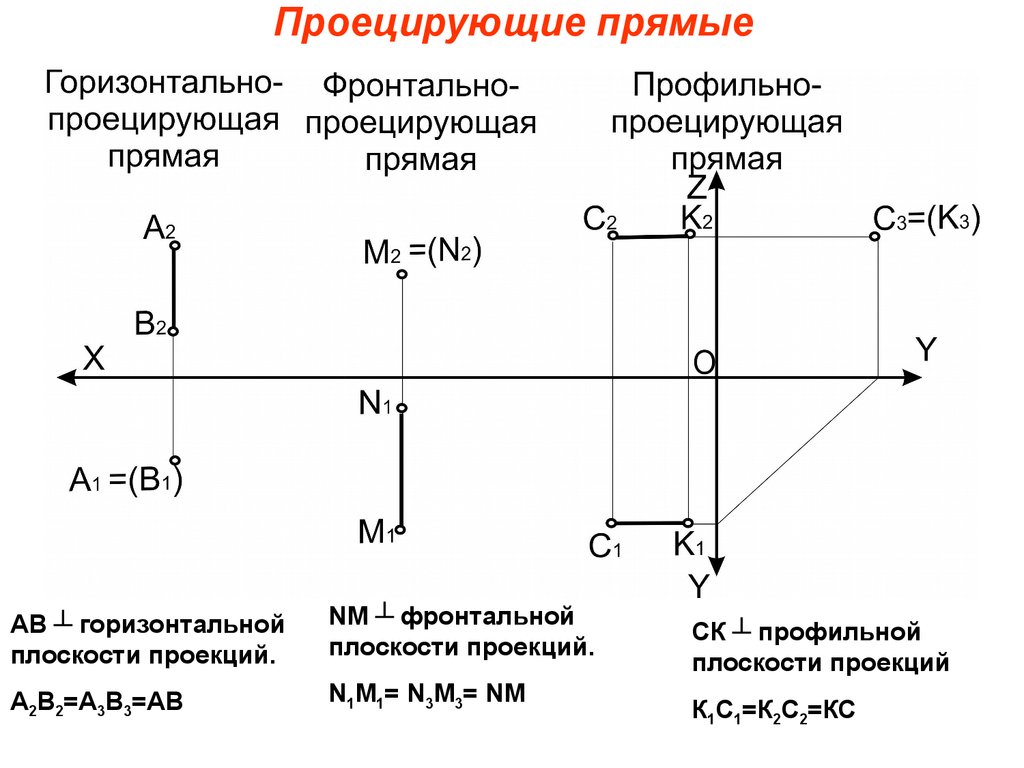
36. Проецирующие прямые Горизонтально проецирующая прямая
z zB2B2
B3B3
HBHB
AB AB
A 2 A2
HBHB
AB AB
АВ
перпендикулярна
горизонтальной
плоскости
проекций
A3 A3
x x
y y
(A1A)1 BB11
АВ - горизонтальнопроецирующая прямая
y y
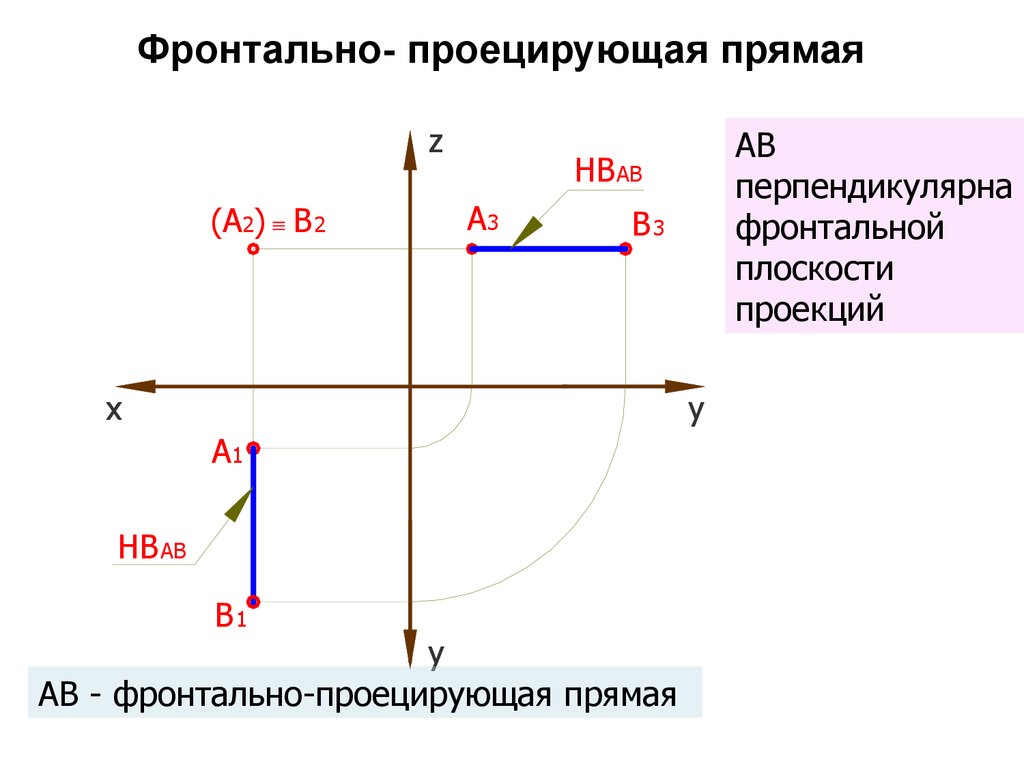
37. Фронтально- проецирующая прямая
zA
B 2B 2
(A2
2)
АВ
перпендикулярна
фронтальной
плоскости
проекций
HB AB
A3
B3
x
y
A1
HB AB
B1
y
АВ - фронтально-проецирующая прямая
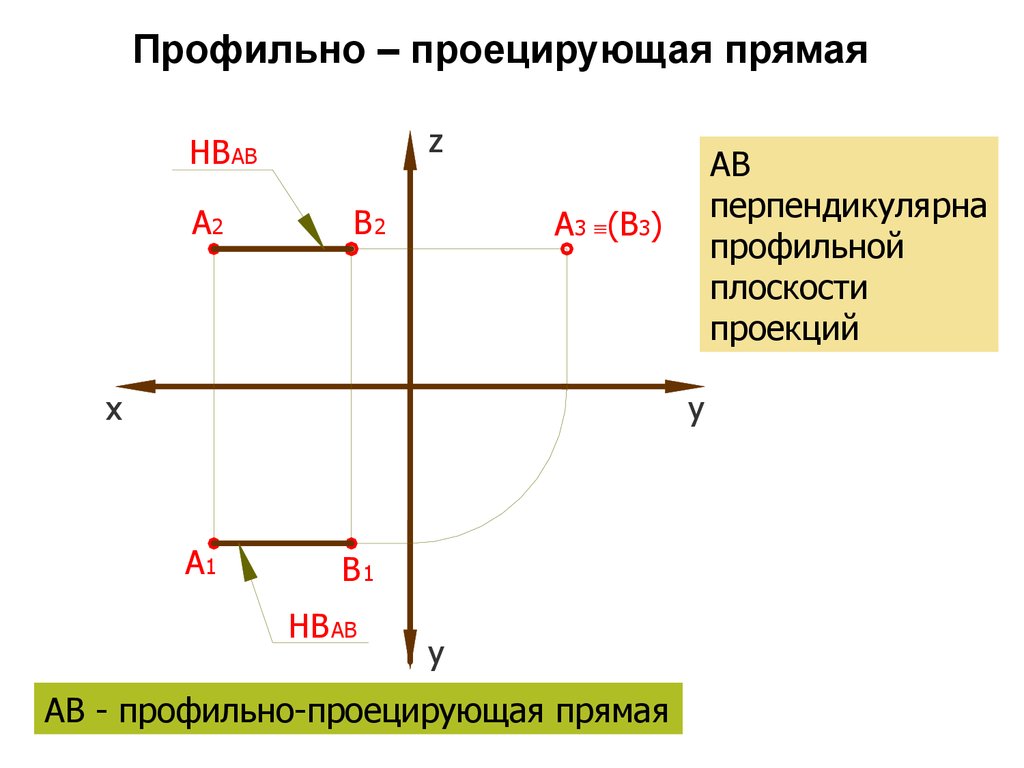
38. Профильно – проецирующая прямая
zHB AB
A2
B2
АВ
перпендикулярна
профильной
плоскости
проекций
A3 (B
B 33)
x
y
A1
B1
HB AB
y
АВ - профильно-проецирующая прямая
39. Проецирующие прямые
АВ ┴ горизонтальнойплоскости проекций.
NM ┴ фронтальной
плоскости проекций.
А2В2=А3В3=АВ
N1M1= N3M3= NM
СК ┴ профильной
плоскости проекций
К1С1=К2С2=КС
40. Следы прямой
• Точки пересечения прямой линии сплоскостями проекции называются следами
прямой.
• Точка пересечения прямой с горизонтальной
плоскостью проекций называется
горизонтальным следом прямой.
• Точка пересечения прямой с фронтальной
плоскостью проекций называется
фронтальным следом прямой.
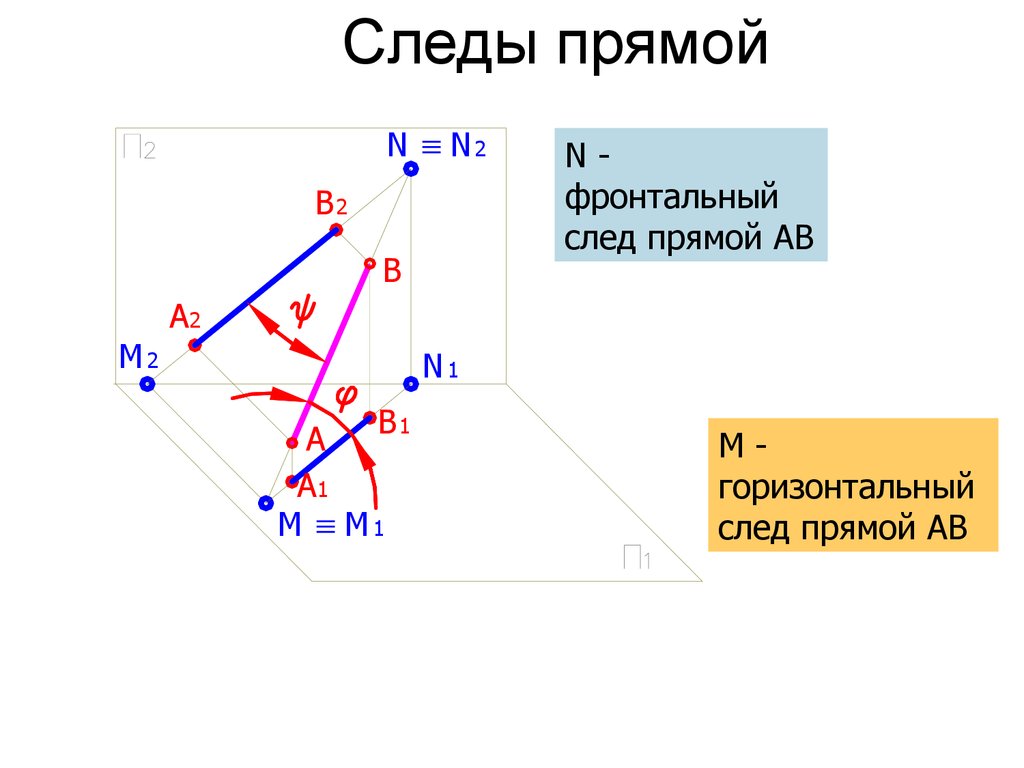
41. Следы прямой
N N 2B2
B
M 2
Nфронтальный
след прямой АВ
A2
N 12
B1
A
A1
M M 1
Мгоризонтальный
след прямой АВ
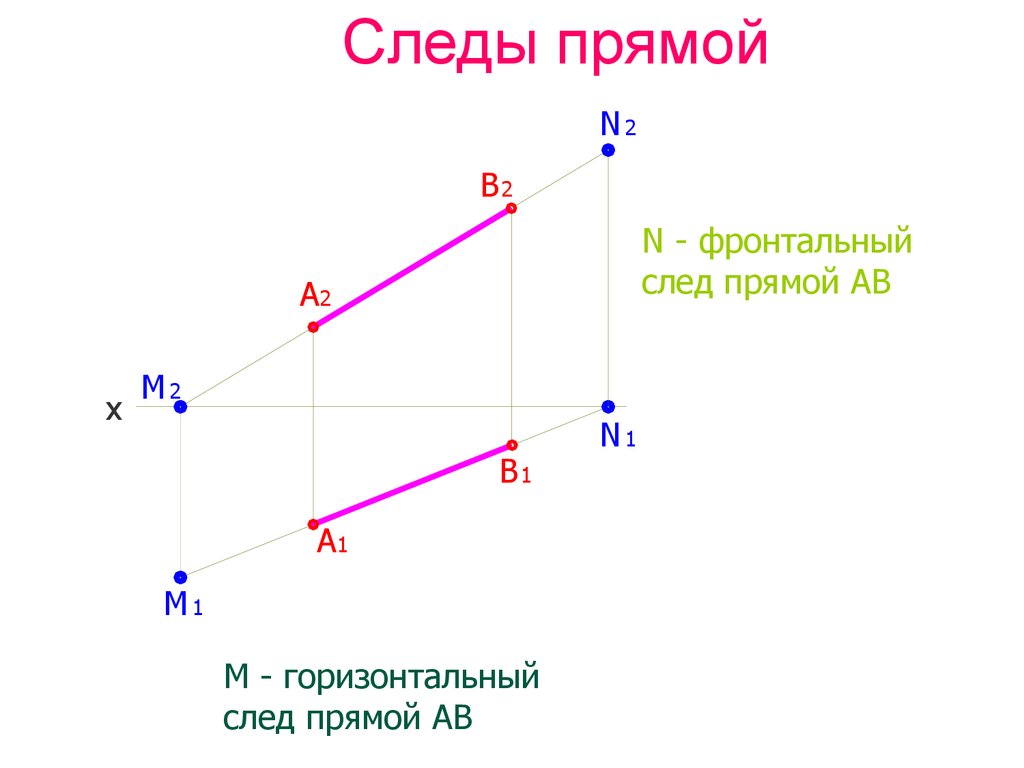
42. Следы прямой
N2B2
N - фронтальный
след прямой АВ
A2
x
M2
B1
A1
M1
М - горизонтальный
след прямой АВ
N1
43. Относительное положение прямых
Прямые относительно друг друга могут располагаться:1. Параллельно;
2. Перпендикулярно;
3. Пересекаться;
4. Скрещиваться.
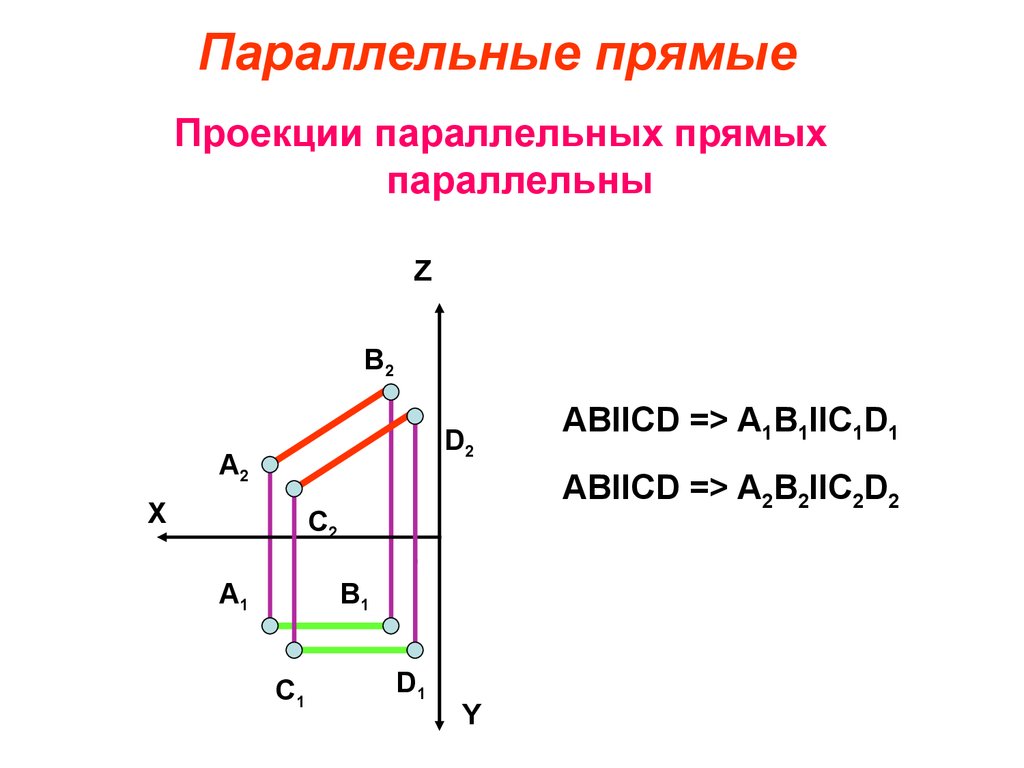
44. Параллельные прямые
Проекции параллельных прямыхпараллельны
Z
В2
D2
А2
X
ABIICD => A2B2IIC2D2
C2
А1
В1
C1
ABIICD => A1B1IIC1D1
D1
Y
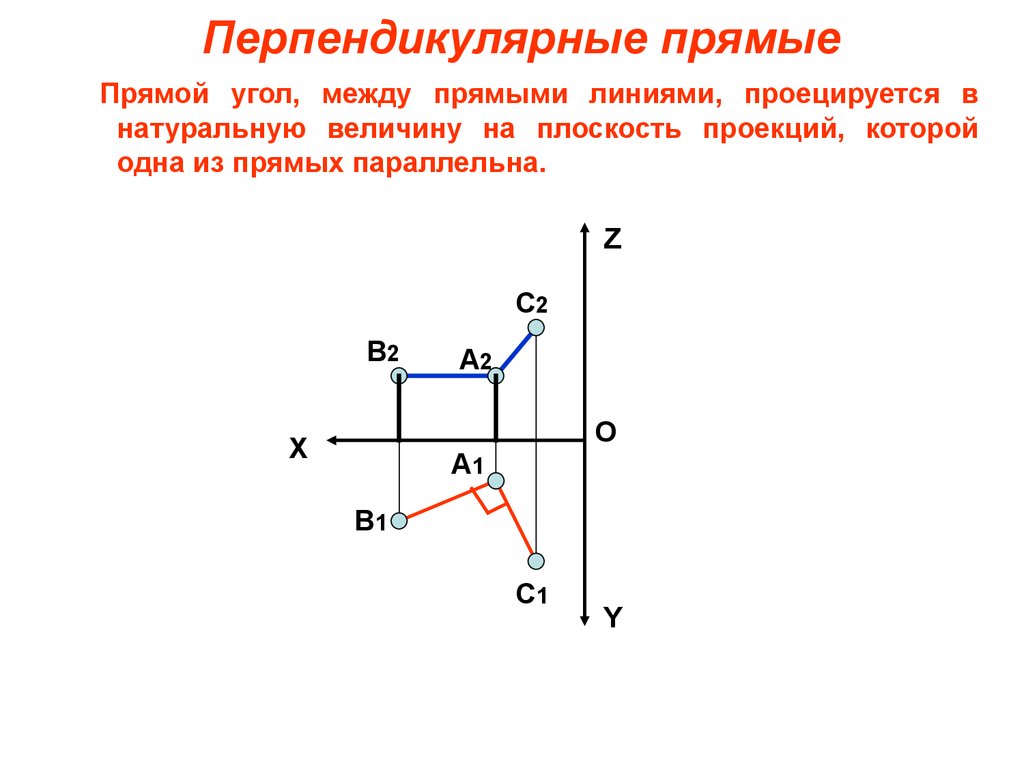
45. Перпендикулярные прямые
Прямой угол, между прямыми линиями, проецируется внатуральную величину на плоскость проекций, которой
одна из прямых параллельна.
Z
C2
B2
A2
O
X
A1
B1
C1
Y
46. Скрещивающиеся и пересекающиеся прямые.
m 2m 2 22 22 (32)n 2n 2
m 1m 1
n 1n 11
52
12 12
31
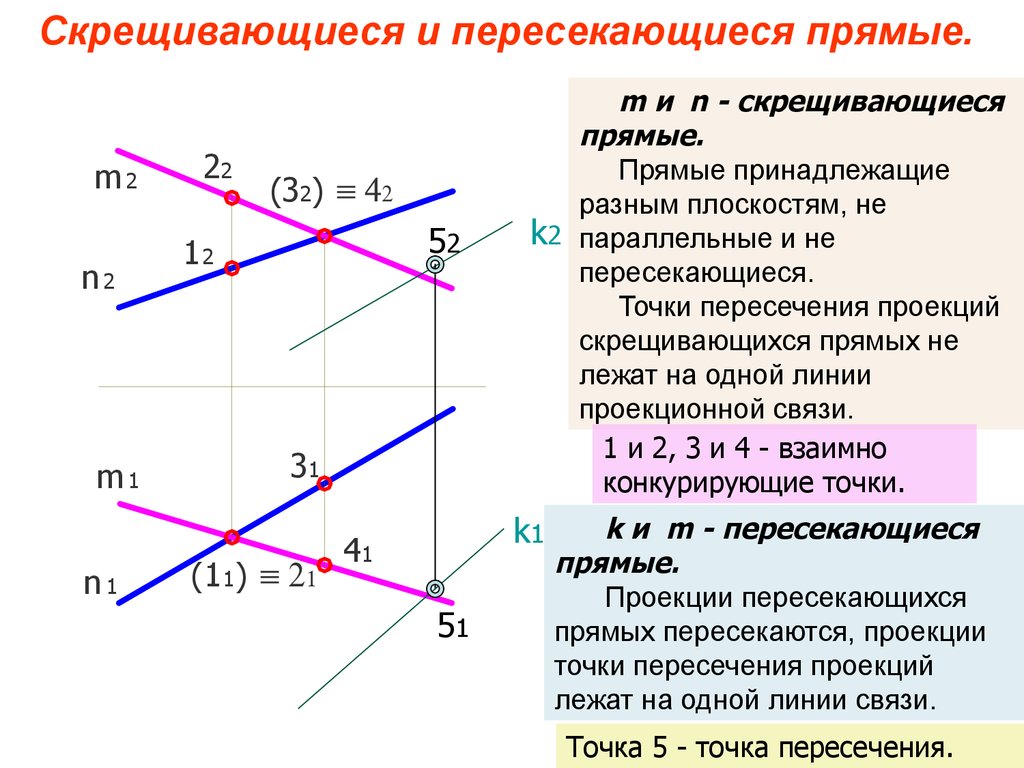
m и n - скрещивающиеся
прямые.
Прямые принадлежащие
разным плоскостям, не
k2 параллельные и не
пересекающиеся.
Точки пересечения проекций
скрещивающихся прямых не
лежат на одной линии
проекционной связи.
1 и 2, 3 и 4 - взаимно
конкурирующие точки.
k1
41
1)11
(1 1(1
)
51
k и m - пересекающиеся
прямые.
Проекции пересекающихся
прямых пересекаются, проекции
точки пересечения проекций
лежат на одной линии связи.
Точка 5 - точка пересечения.
47. Контрольные вопросы
1. Построить точку А(35,10,25).2. Построить точку В(35,10,25).
3. Построить следы отрезка прямой АВ.
А(35,10,25); В(60,40,10).
4. Название прямой перпендикулярной
фронтальной плоскости проекций.
5. Название прямой, параллельной
горизонтальной плоскости проекций.

















 Инженерная графика
Инженерная графика








