Похожие презентации:
Теплообмен. Основные понятия теории теплообмена
1. ТЕПЛООБМЕН
2. 1 ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ТЕПЛООБМЕНА
3. 1.1 Виды теплообмена
Три основных способа переносатеплоты, отличающихся по своим
физическим механизмам:
теплопроводность,
конвекция,
излучение.
За
счет
излучения
теплота
передается во всех лучепрозрачных
средах, в том числе и в вакууме.
4. 1.2 Основные понятия и определения
Легкоподвижная среда (жидкость или газ), используемаядля переноса теплоты, называется теплоносителем.
Поверхность теплообмена F – это поверхность, через
которую происходит передача теплоты
Тепловой поток, Q, [Вт] – это количество теплоты,
передаваемое через поверхность теплообмена F в единицу
времени. В отличие от теплоты тепловой поток является
векторной величиной, имеющей направление. Тепловой
поток направлен в сторону распространения теплоты, т.е. в
сторону наибольшего уменьшения температуры.
5.
Поверхностная плотность теплового потока q, [Вт/м²] –это количество теплоты, передаваемое в единицу времени
через единичную площадь поверхности теплообмена.
Q
q
F
Линейная плотность теплового потока ql, [Вт/м]– это
тепловой поток через единицу длины цилиндрической
стенки
Q
ql
L
6.
Температурным полем называется совокупность значений температурыво всех точках рассматриваемого пространства в данный момент
времени.
t= f (x,y,z,τ)
где t – температура; x, y, z – пространственные координаты; τ – время.
Температурное поле, зависящее от времени - нестационарное
(неустановившийся тепловой режим).
Когда распределение температуры не изменяется со временем,
температурное поле называется стационарным (установившийся тепловой
режим):
t= f (x,y,z)
Поверхность, во всех точках которой температура одинакова, называется
изотермической.
Изотермические поверхности или замыкаются на себя или кончаются на
границах тела, но между собой никогда не пересекаются. Температура в
теле изменяется лишь в направлении, пересекающем изотермы
7.
Градиент температурного поля (grad t) – естьвектор, направленный по нормали к изотермической
поверхности в сторону наибольшего возрастания
температуры и численно равный производной от
температуры по этому направлению.
8.
2 ТЕОРИЯ ТЕПЛОПРОВОДНОСТИ9.
Под теплопроводностью следуетпонимать процесс переноса теплоты
через соприкосновение структурных
частиц
тела
(атомов,
молекул,
электронов и др.). В разных средах
механизм передачи теплоты может
отличаться.
10. 2.1 Закон Фурье
Поверхностнаяплотность
теплового
потока,
передаваемого теплопроводностью, пропорциональна
градиенту температурного поля:
q= - λ ∙ grad t , Вт/м²
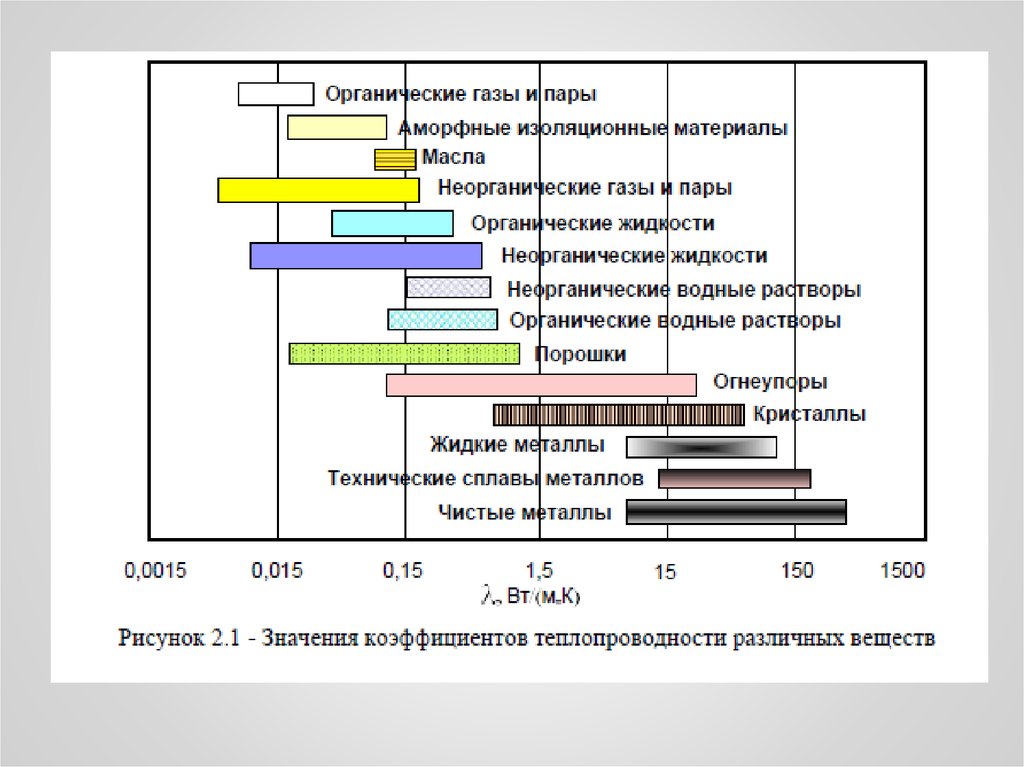
где λ – коэффициент теплопроводности, Вт/(м∙К) характеризует способность вещества, из которого состоит
рассматриваемое тело, проводить теплоту.
Знак «–» указывает на противоположные направления
вектора
теплового
потока
и
вектора
градиента
температурного поля. Вектор плотности теплового потока q
всегда направлен в сторону наибольшего уменьшения
температуры.
11.
Численное значение коэффициента теплопроводности λравно количеству теплоты, проходящей через единицу
изотермической поверхности в единицу времени, при
условии, что градиент температуры равен 1 град/м.
Коэффициент теплопроводности является физическим
параметром и зависит от химической природы вещества и
его физического состояния (плотности, влажности,
давления, температуры).
12.
13. 2.2 Дифференциальное уравнение теплопроводности
Дифференциальноеуравнение
теплопроводности
(уравнение Фурье) нестационарного температурного поля
t
a
где а = λ /(с∙ρ) – коэффициент температуропроводности тела, м²/с.
Это физическая величина, характеризующая скорость
изменения температуры в теле и его теплофизические
свойства. Зависит от природы вещества и его физического
состояния.
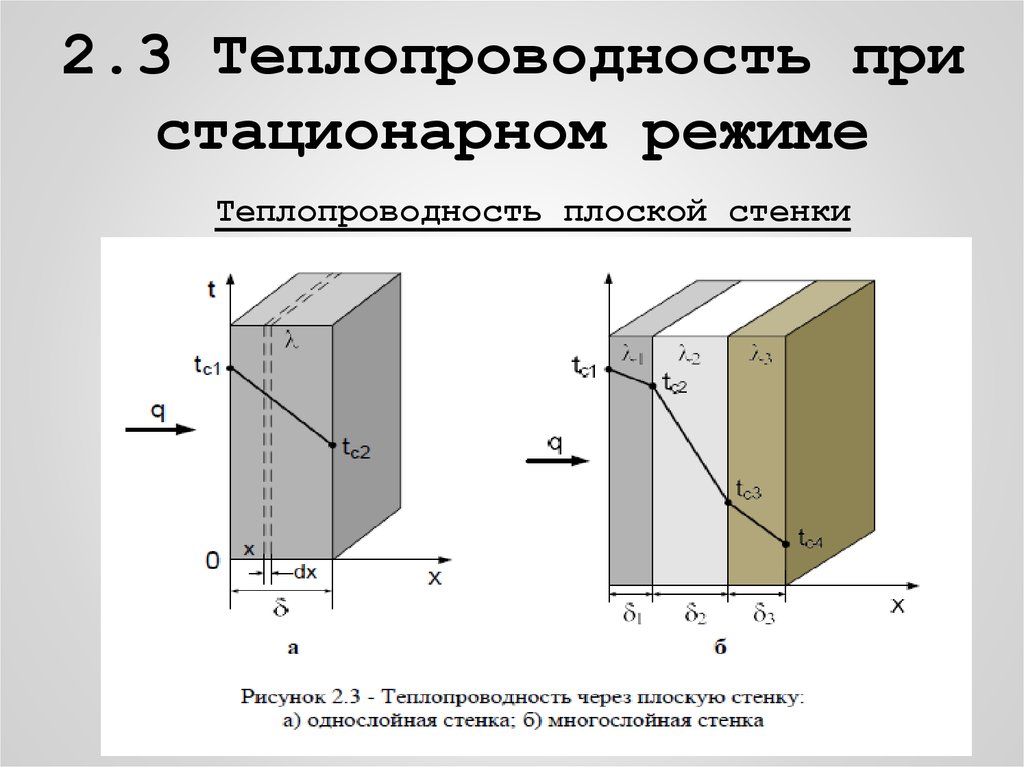
14. 2.3 Теплопроводность при стационарном режиме
Теплопроводность плоской стенки15.
Поверхностная плотность теплового потока:( t c1 t c 2 )
dt
q
dx
q
t
t
R
t t c1 t c 2
R / -
внутреннее термическое сопротивление
теплопроводности стенки, (м2 К)/Вт.
Распределение температур в плоской однородной
стенке - линейное.
Тепловой поток (мощность теплового потока) :
Q q F ( t c1 t c2 ) F
16.
Рассмотрим для тех же условий многослойную плоскуюстенку с толщиной слоев 1, 2,…, n с оответствующими
коэффициентами теплопроводности 1, 2,…, n. Здесь
слои плотно прилегают друг к другу.
Плотность теплового потока многослойной плоской
стенки:
t c1 t c ( n 1 )
t
q
n
n
i
R i
i 1 i
i 1
где n - число слоев многослойной стенки;
tc1 и tc(n+1) - температуры на внешних границах
многослойной стенки;
n
R i - полное термическое сопротивление многослойной
i 1
плоской стенки.
17.
Плотность теплового потока, проходящего черезвсе слои, в стационарном режиме одинакова.
Коэффициент теплопроводности различен, то для
плоской многослойной стенки распределение температур
- ломанная линия.
Для k-го слоя температуру на границе любого слоя
можно записать:
k
t c ( k 1 ) t c1 q R i
i 1
18.
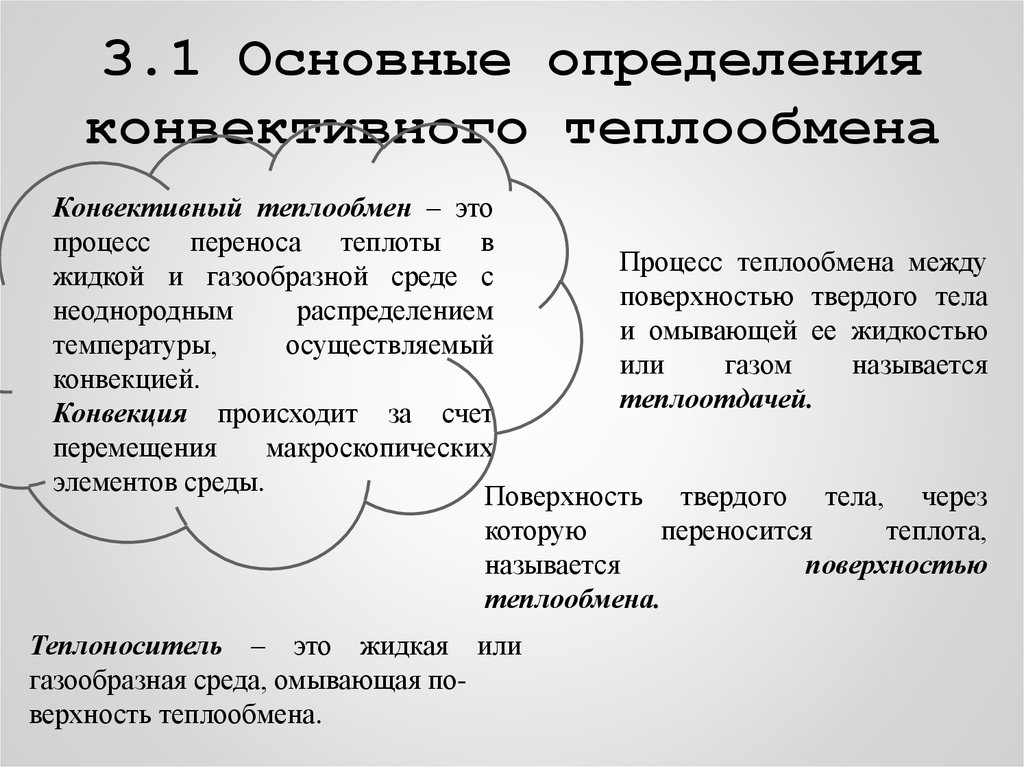
3 КОНВЕКТИВНЫЙ ТЕПЛООБМЕН19. 3.1 Основные определения конвективного теплообмена
Конвективный теплообмен – этопроцесс переноса теплоты в
Процесс теплообмена между
жидкой и газообразной среде с
поверхностью твердого тела
неоднородным
распределением
и омывающей ее жидкостью
температуры,
осуществляемый
или
газом
называется
конвекцией.
теплоотдачей.
Конвекция происходит за счет
перемещения
макроскопических
элементов среды.
Поверхность твердого тела, через
которую
переносится
теплота,
называется
поверхностью
теплообмена.
Теплоноситель – это жидкая или
газообразная среда, омывающая поверхность теплообмена.
20. 3.2 Виды конвективного теплообмена
Естественная конвекция - свободное движение,происходящее вследствие разности плотностей нагретых и
холодных частиц жидкости, находящихся в поле действия
сил тяжести.
Она тем сильнее, чем больше разность температур
между поверхностью теплообмена и жидкостью (Δt = tc–tж)
и температурный коэффициент объемного расширения:
1 v
v T p const
где =1/ - удельный объем жидкости.
21.
Вынужденная конвекция создается внешнимисточником
(насосом,
вентилятором,
ветром).
Вынужденная конвекция тем интенсивнее, чем больше
скорость вынужденного движения.
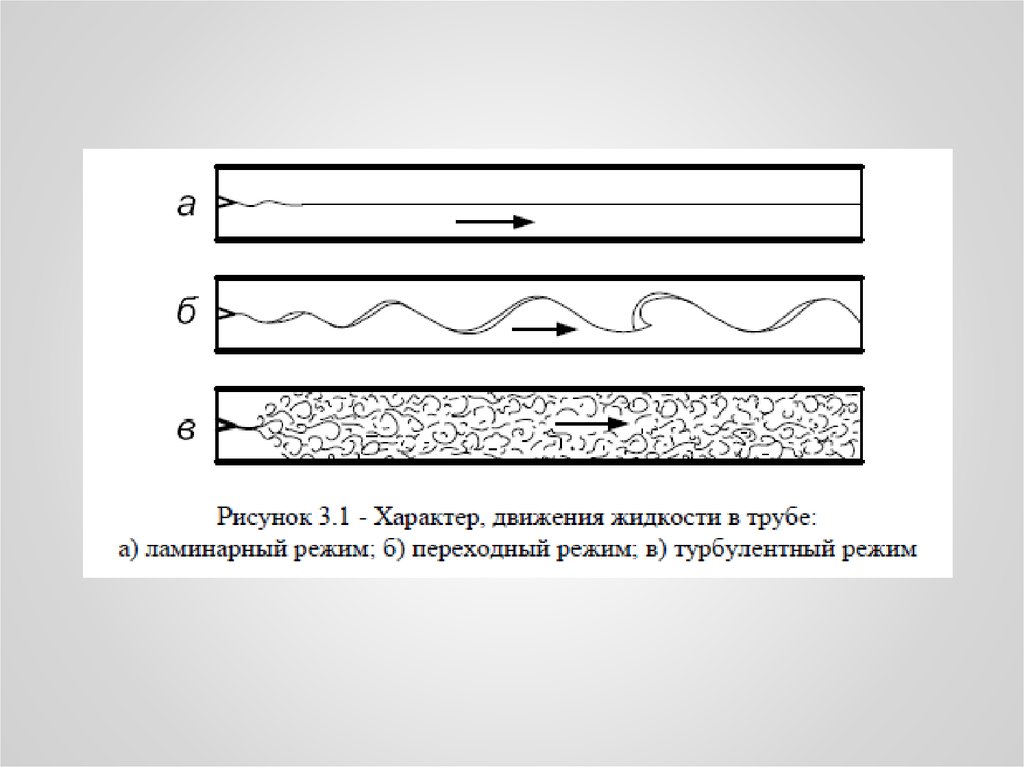
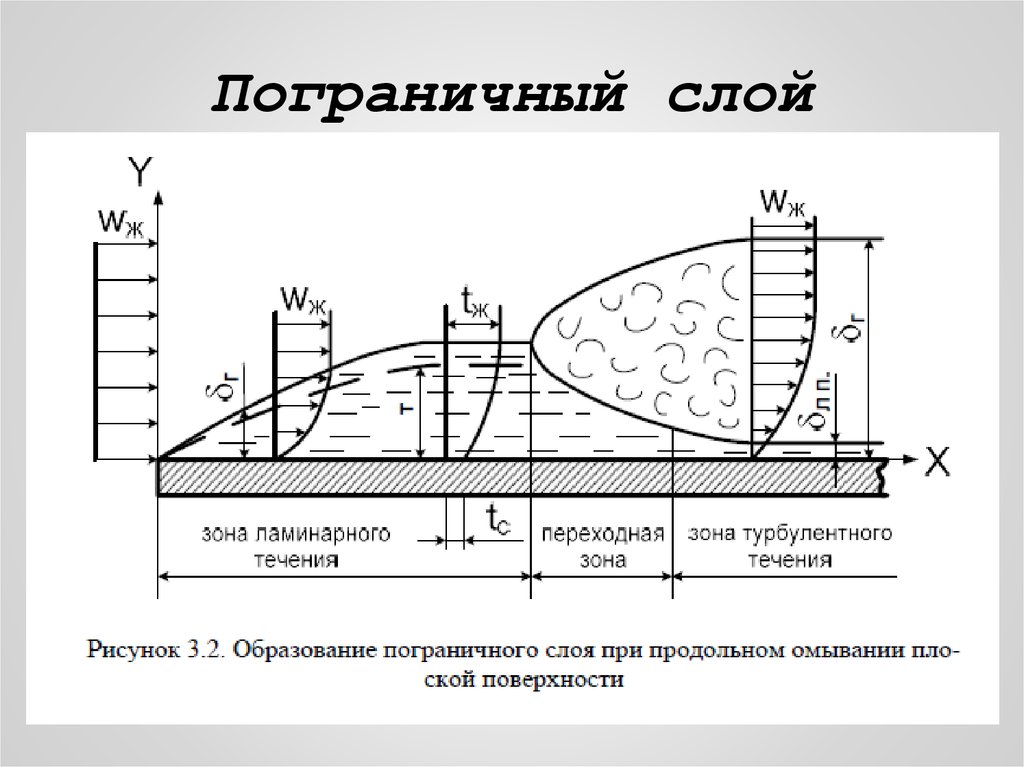
22. 3.3 Режимы течения и пограничный слой
Интенсивность конвективного теплообмена сильнозависит от режима течения омывающей жидкости.
Различают три режима течения :
☼ - ламинарный,
☼ - переходный,
☼ - турбулентный.
23.
24.
Режим течения характеризуется критерием Рейнольдса:Re
w l
где w – скорость движения жидкости, м/с;
l – характерный размер канала или обтекаемой стенки, м;
ν– кинематическая вязкость жидкости, м2/с.
Ламинарный режим характеризуется спокойным послойным движением
частиц жидкости, без перемешивания
Re < ReкрI
При турбулентном режиме – течение жидкости вихревое, с
непрерывным перемешиванием всех слоев
Re > ReкрII
где ReкрI и ReкрII –критические числа Рейнольдса.
Переходным называется режим движения жидкости, промежуточный
между ламинарным и турбулентным. Интервал существования
переходного режима ограничивается критическими значениями ReкрI и
ReкрII.
25. Пограничный слой
26. 3.4 Закон Ньютона-Рихмана
Для пограничного слоя:Q F grad t T F tc tж
Закон Ньютона-Рихмана:
Тепловой поток Q, Вт, в процессе теплоотдачи
пропорционален площади поверхности теплообмена F и
разности температур поверхности стенки tc и жидкости
tж:
Q F tc tж
27.
Коэффициент теплоотдачи α – это количество теплоты,передаваемое в единицу времени через единицу площади
поверхности при разности температур поверхности и
жидкости в один градус, Вт/(м²∙К).
Характеризует интенсивность процесса теплоотдачи и
зависит от физических свойств жидкости и характера ее
движения.
28. 3.5 Факторы, влияющие на интенсивность конвективного теплообмена
1.Режим течения и ламинарный подслой2.Направление теплового потока
3.Форма и размеры поверхности теплообмена
4.Теплофизические свойства жидкости
5.Вид конвективного теплообмена
29. 3.7 Теория подобия
3.7.1 Основы теории подобияТеория подобия – это учение о подобных явлениях.
Подобными физическими явлениями называются такие
явления, которые проходят в геометрически подобных
системах, у которых во всех сходственных точках пространства
и в сходственные моменты времени отношение одноименных
физических величин есть числа постоянные.
30. 3.7.2 Критерии (числа) подобия
Числами (критериями) подобия называются такиебезразмерные соотношения параметров, характеризующих
рассматриваемый процесс, которые у подобных явлений в
сходственных точках имеют численно одинаковые
значения.
В теории конвективного теплообмена используются
следующие числа подобия:
31.
Число Нуссельтаl
Nu
где α - коэффициент теплоотдачи, Вт/(м²·К);
l - определяющий размер, м;
λ - коэффициент теплопроводности, Вт/(м·К).
Nu характеризует увеличение теплообмена конвекцией по
сравнению с чистой теплопроводностью.
32. Число Рейнольдса
Rew l
где w - скорость движения жидкости, м/с;
l - определяющий размер, м;
ν - коэффициент кинематической вязкости, м²/с.
Re представляет собой безразмерную скорость потока,
характеризует гидродинамический режим потока. Re выражает
отношение сил инерции (скоростного напора) к силам вязкого
трения.
При течении жидкости в трубах:
Re <2300 - ламинарный режим,
Re = 2300…104 - переходный режим,
Re>104 - турбулентный режим.
33. Число Прандтля
Pra
c
где ν - коэффициент кинематической вязкости, м²/с;
а - коэффициент температуропроводности, м²/с.
Pr является теплофизической константой вещества. Значения
Pr приводятся в справочниках.
Pr является мерой подобия скоростных и температурных полей
в потоке. Для вязких жидкостей Pr >1 и сильно зависит от
температуры. Для газов величина Pr определяется атомностью:
- для одноатомных газов Pr = 0,67;
- для двухатомных газов Pr = 0,72;
- для трехатомных газов Pr = 0,80;
- для четырехатомных газов Pr = 1,0.
34. Число Грасгофа
Grg t l
3
2
где g = 9,81 м/с² - ускорение свободного падения;
β=1/Т - коэффициент объемного расширения, 1/К;
l - определяющий размер, м;
Δt = tc - tж - разность температур, °С (К);
ν - коэффициент кинематической вязкости, м²/с.
Gr характеризует подъемную силу, возникающую в
жидкости вследствие разности плотностей. Показывает
влияние естественной конвекции на теплообмен.
35. Число Фурье
aFo 2
l
где а - коэффициент температуропроводности, м²/с;
l - определяющий размер, м;
τ - время, с.
Fo представляет собой безразмерное время и
характеризует нестационарность процесса теплообмена.
36.
Таким образом:критерий Re отражает влияние вынужденного
движения,
критерий Gr – влияние естественной конвекции,
критерий Pr – влияние физических свойств жидкости
на коэффициент теплоотдачи;
критерий Fo - нестационарность процесса.
Числа Nu, Pr, Gr, Fo – являются числами теплового
подобия. Re – число гидродинамического подобия.
37. 3.7.3 Определяющие размер и температура
В числа подобия входит характерный линейный размер l,называемый определяющим размером.
Для потока в круглой трубе - внутренний диаметр dвн ,
при поперечном омывании трубы - наружный диаметр
трубы dн;
при свободной естественной конвекции - ширина b, длина l,
или высота h поверхности теплообмена.
38.
Определяющая температура – это температура, при которойопределяются физические свойства жидкости в числах подобия.
При свободной конвекции в неограниченном пространстве температура половинного слоя tm = 0,5 (tж +tc);
при течении жидкости в трубе - температура стенки tc или
средняя температура жидкости tж.
Определяющие размер и температура записываются индексом к
критерию. Например,
Re ж , d вн
w dв н
ж
39. 3.7.4 Теоремы подобия
Основныеположения
теории
подобия
формулируются в виде трех теорем.
Две из них говорят о явлениях, подобие которых
заранее известно, и формулируют основные свойства
подобных между собой явлений.
Третья теорема обратная. Она устанавливает
признаки, по которым можно узнать, подобны ли два
явления друг другу.
40. Первая теорема подобия (теорема Ньютона)
Первая теорема подобия для подобного течения двухжидкостей была высказана И.Ньютоном в 1686 г. Однако
строгое доказательство теоремы было дано Ж.Бертраном
в 1848 г.
У подобных явлений индикаторы подобия равны
единице, или у подобных явлений числа подобия
численно одинаковы.
Первая теорема подобия устанавливает связь между
константами подобия и позволяет вывести уравнения для
чисел подобия.
41. Вторая теорема подобия (теорема Букингема)
Вторая теорема подобия была доказана в 1911 г. русскимученым А.Федерманом и в 1914 г. американским ученым
Е.Букингемом.
Если физическое явление описывается системой
дифференциальных уравнений, то всегда существует
возможность представления их в виде уравнений
подобия, т.е. интеграл дифференциального уравнения
может быть представлен как функция чисел подобия
дифференциального уравнения.
Вторая
теорема
разрешает
искать
решение
дифференциального уравнения в виде уравнения подобия..
42. Третья теорема подобия (теорема Кирпичева)
Формулировка третьей теоремы подобия была дана М.В.Кирпичевым иА.А.Гухманом, а доказательство теоремы - М.В.Кирпичевым в 1933 г.
Подобны те явления, условия однозначности которых подобны и числа
подобия, составленные из условий однозначности, численно
одинаковы.
Условия однозначности:
Явления протекают в геометрически подобных системах;
Для рассматриваемого явления можно составить дифференциальное
уравнение;
Установлены существование и единственность решения уравнения при
заданных граничных условиях;
Известны числовые значения коэффициентов и физических параметров,
входящих в дифференциальное уравнение.
Третья теорема устанавливает необходимые условия для того, чтобы
явления оказались подобными друг другу.
43. 3.8 Уравнения подобия конвективного теплообмена
Уравнением подобия называется зависимость между какимлибо определяемым числом подобия и другимиопределяющими числами подобия.
При решении задач на конвективный теплообмен искомым
является коэффициент теплоотдачи α и определяемым числом
подобия является Nu (только в это число входит α).
Прочие числа подобия (Re, Gr, Pr, Fo) являются определяющими
- с их помощью рассчитывается численное значение Nu.
При конвективном теплообмене уравнение подобия в общем
случае имеет вид
Nu = f (Re,Gr,Pr,Fo),
где Nu, Re, Gr, Pr, Fo – числа подобия, характеризующие
процесс теплообмена и гидродинамики.
44.
Функциональнаязависимость
коэффициента имеет вид:
безразмерного
• при стационарной теплоотдаче и естественной
конвекции
• Nu = f (Gr,Pr),
• при нестационарном режиме и ламинарном течении
жидкости
• Nu= f (Re,Gr,Pr,Fo),
• при стационарном режиме и турбулентном течении
жидкости
Nu= f (Re,Pr).
45.
Дифференциальныеуравнения,
условия
однозначности и теоремы подобия позволили получить
уравнение подобия стационарного теплообмена в
общем виде:
Nu C Re Gr Pr
m
n
P
где С – безразмерный коэффициент;
m, n, p – безразмерные степенные показатели,
принимающие
различные
значения
для
соответствующих интервалов изменения Re, Gr и Pr.








































 Физика
Физика








