Похожие презентации:
Техническая термодинамика и теплопередача
1. Теплотехника Техническая термодинамика и теплопередача
Овсянников М.К. И.И., ОрловаЕ.Г., Костылев
ФГБОУ ГУМРФ
2. Часть 2
ФГБОУ ГУМРФ3. Оглавление
ВВЕДЕНИЕРАЗДЕЛ II. ТЕПЛОПЕРЕДАЧА
Глава 11.ТЕПЛОПРОВОДНОСТЬ
Глава 12. КОНВЕКТИВНЫЙ
ТЕПЛООБМЕН
Глава 13. ТЕПЛОПЕРЕДАЧА
Глава 14. ЛУЧИСТЫЙ ТЕПЛООБМЕН
Глава 15. ОСНОВЫ РАСЧЕТА
ТЕПЛООБМЕННЫХ АППАРАТОВ
Приложения
ФГБОУ ГУМРФ
4. Глава 11.ТЕПЛОПРОВОДНОСТЬ 11.1. Температурное поле и температурный градиент 11.2. Тепловой поток. Основной закон теплопроводности 11.3. Коэффиц
Глава 11.ТЕПЛОПРОВОДНОСТЬ11.1. Температурное поле и температурный градиент
11.2. Тепловой поток. Основной закон
теплопроводности
11.3. Коэффициент теплопроводности
11.4. Дифференциальное уравнение
теплопроводности
11.5. Условия однозначности (краевые условия) задач
теплопроводности
11.6. Способы задания граничных условий
теплообмена
11.7. Стационарная теплопроводность через
однослойную плоскую стенку.
ФГБОУ ГУМРФ
5. 11.8. Стационарная теплопроводность через многослойную плоскую стенку 11.9. Теплопроводность через цилиндрическую стенку 11.10. Сравнение теп
11.8. Стационарная теплопроводность черезмногослойную плоскую стенку
11.9. Теплопроводность через цилиндрическую
стенку
11.10. Сравнение теплопроводности
цилиндрической и плоской стенок
11.13. Теплопроводность через многослойную
цилиндрическую стенку
11.14. Теплопроводность в стержне постоянного
поперечного сечения
11.15. Нестационарная теплопроводность.
Понятие о регулярном режиме
Контрольные вопросы и задания к главе 11
ФГБОУ ГУМРФ
6. Глава 12. КОНВЕКТИВНЫЙ ТЕПЛООБМЕН 12.1. Понятия и определения 12.2 Дифференциальные уравнения конвективного теплообмена 12.3. Основы теории под
Глава 12. КОНВЕКТИВНЫЙ ТЕПЛООБМЕН12.1. Понятия и определения
12.2 Дифференциальные уравнения конвективного
теплообмена
12.3. Основы теории подобия
12.4. Числа гидромеханического подобия
12.5. Числа теплового подобия
12.6. Критериальные уравнения конвективного
теплообмена
12.7. Теплообмен в свободном потоке жидкости
(естественная конвекция)
12.8. Теплообмен в вынужденном потоке жидкости
(вынужденная конвекция)
12.8.1. Режимы движения вязкой жидкости
12.8.2. Понятие пограничного слоя
ФГБОУ ГУМРФ
7. 12.8.3. Осреднение параметров потока 12.8.4. Теплоотдача в каналах при ламинарном режиме движения жидкости 12.8.5. Теплоотдача в каналах при турбул
12.8.3. Осреднение параметров потока12.8.4. Теплоотдача в каналах при ламинарном
режиме движения жидкости
12.8.5. Теплоотдача в каналах при турбулентном
режиме движения жидкости
12.8.6. Теплоотдача при поперечном омывании
гладких труб
12.8.7. Теплоотдача при поперечном омывании
пучков труб
12.8.8. Теплоотдача при движении жидкости
вдоль плоской стенки
12.9. Конвективный теплообмен при изменении
агрегатного состояния
Контрольные вопросы и задания к главе 12
ФГБОУ ГУМРФ
8. Глава 13. ТЕПЛОПЕРЕДАЧА 13.1. Теплопередача от среды к среде через многослойную плоскую стенку 13.2. Эквивалентная стенка 13.3. Теплопередача че
Глава 13. ТЕПЛОПЕРЕДАЧА13.1. Теплопередача от среды к среде
через многослойную плоскую стенку
13.2. Эквивалентная стенка
13.3. Теплопередача через цилиндрическую
стенку. Термическое сопротивление
теплопередаче
13.4. Понятие о критической толщине
изоляции
Контрольные вопросы и задания к главе 13
ФГБОУ ГУМРФ
9. Глава 14. ЛУЧИСТЫЙ ТЕПЛООБМЕН 14.1. Определения 14.2. Основные законы теплового излучения 14.3. Излучение газов 14.4. Излучение между твердыми тел
Глава 14. ЛУЧИСТЫЙ ТЕПЛООБМЕН14.1. Определения
14.2. Основные законы теплового
излучения
14.3. Излучение газов
14.4. Излучение между твердыми
телами.
Контрольные вопросы и задания к
главе 14
ФГБОУ ГУМРФ
10. Глава 15. ОСНОВЫ РАСЧЕТА ТЕПЛООБМЕННЫХ АППАРАТОВ 15.1. Определения 15.2. Основы расчета рекуперативного теплообменника 15.3. Теплообменники с ор
Глава 15. ОСНОВЫ РАСЧЕТАТЕПЛООБМЕННЫХ АППАРАТОВ
15.1. Определения
15.2. Основы расчета рекуперативного
теплообменника
15.3. Теплообменники с органическим
теплоносителем
15.4. Особенности расчета теплообмена в
установках с термомаслом
Контрольные вопросы и задания к главе 15
ФГБОУ ГУМРФ
11. Приложения 1. Задачи. Решения 2. Таблицы теплофизических свойств жидкостей, газов и твердых тел
Приложения1. Задачи. Решения
2. Таблицы теплофизических свойств
жидкостей, газов и твердых тел
ФГБОУ ГУМРФ
12. Условные обозначения
Раздел II. Теплопередачаα, Вт/м2·К — коэффициенты теплоотдачи;
k, Вт/м2·К — коэффициент теплопередачи;
kℓ, Вт/м·К — погонный коэффициент теплопередачи;
G, кг/с — массовый расход;
Gυ, м3/с — объемный расход;
W, (м/с) — скорость;
w
— число Рейнольдса;
Re
Nu
— число Нуссельта;
ФГБОУ ГУМРФ
13. Условные обозначения
Рr — число Прандтля при средней температурепотока;
Рrw — число Прандтля при температуре стенки;
Gr
g 3 t
2
— число Грасгофа;
Fr — число Фруда;
Eu — число Эйлера;
Pe — число Пекле;
Fo — число Фурье;
ср, кДж/кг·К — удельная изобарная теплоемкость;
ФГБОУ ГУМРФ
14. Условные обозначения
ρ, кг/м3 — плотность теплоносителя при средней температуре;λ, Вт/м·К — коэффициент теплопроводности;
λw, Вт/м·К — коэффициент теплопроводности материала
стенки;
, м/с2 — кинематический коэффициент вязкости;
ℓ, м — характерный размер;
Q, кВт — тепловая мощность;
Qo, Дж — абсолютное количество тепла;
q, Вт/м2 — плотность теплового потока;
Δtл, ˚С — среднелогарифмический перепад температур;
, ˚С — температура горячей среды на входе в
t гор
теплообменник;
t гор
, ˚С — температура горячей среды на выходе из
теплообменника;
ФГБОУ ГУМРФ
15. Условные обозначения
t хол, ˚С — температура холодной среды на входе в
теплообменник;
t хол
, ˚С — температура холодной среды на выходе из
теплообменника;
F, м2 — площадь теплообменной поверхности;
S, м2 — площадь поперечного сечения потока;
dэкв, м — эквивалентный диаметр сечения;
δ, м — толщина стенки;
δп.с., м — толщина пограничного слоя;
E, Вт/м2 — излучательная способность тела;
Iλ, Вт/м3 — интенсивность излучения;
Es, Вт/м2 — интегральная плотность излучения абсолютно
черного тела в вакуум.
ФГБОУ ГУМРФ
16.
Перваячасть
курса
«Техническая
термодинамика» содержит общие сведения
о
параметрах,
характеристиках
и
теплофизических свойствах рабочих сред
судовых энергетических установок (в том
числе газовых смесей и двухфазных смесей)
и способах их определения; изложение
основных
законов
технической
термодинамики;
сведения
о
термодинамических
циклах
тепловых
двигателей и холодильных установок и
оценке их эффективности:
ФГБОУ ГУМРФ
17. Глава 1. ГАЗ КАК РАБОЧЕЕ ТЕЛО. ОСНОВНЫЕ ПАРАМЕТРЫ СОСТОЯНИЯ. УРАВНЕНИЕ СОСТОЯНИЯ
ФГБОУ ГУМРФ18.
Теплообмен можно определить какэнергетическое взаимодействие элементов
вещества с различной температурой.
Научная дисциплина, изучающая процессы
теплообмена, называется теплопередачей.
Есть три различающихся по физической
природе вида теплообмена:
теплопроводность, конвекция и излучение
(радиация). Поэтому и курс теплопередачи
разделен на три соответствующих раздела.
ФГБОУ ГУМРФ
19. Глава 11. ТЕПЛОПРОВОДНОСТЬ
Теплопроводность — перенос теплоты всплошной среде
—
осуществляется
взаимодействием
структурных
частиц
вещества: молекул, атомов и электронов. Это
единственный вид передачи тепла через
твердое тело. Механизм теплопроводности
зависит
от
физических
свойств
теплопередающей среды.
ФГБОУ ГУМРФ
20. 11.1. Температурное поле и температурный градиент
Совокупность значений температуры во всехточках тела называется его температурным
полем: t = t (x, y, z, τ).
Температурные поля могут быть стационарными (не
меняющимися во времени, при этом выполняется
t
условие
,
0
и нестационарными (при разогреве или
охлаждении тела).
ФГБОУ ГУМРФ
21. Температурное поле и температурный градиент
• Точки тела с одинаковой температуройобразуют изотермическую поверхность.
При
пересечении
нескольких
таких
поверхностей
плоскостью
появляется
семейство изотерм.
• Изотермы и изотермические поверхности
различного уровня (с различными t) не
пересекаются и внутри однородного тела
непрерывны, не имеют разрывов.
ФГБОУ ГУМРФ
22. Температурный градиент
• Интенсивность изменения температуры по нормалик
изотермической
поверхности
называется
градиентом температуры, К/м:
t dt
grad n t lim
n 0 n
dn
• Градиент температуры является вектором, всегда
направлен в сторону возрастания температуры и
может быть разложен по координатным осям:
где
i , j, k
t t t
grad n t t i
j
k
x
y
z
— координатные орты.
ФГБОУ ГУМРФ
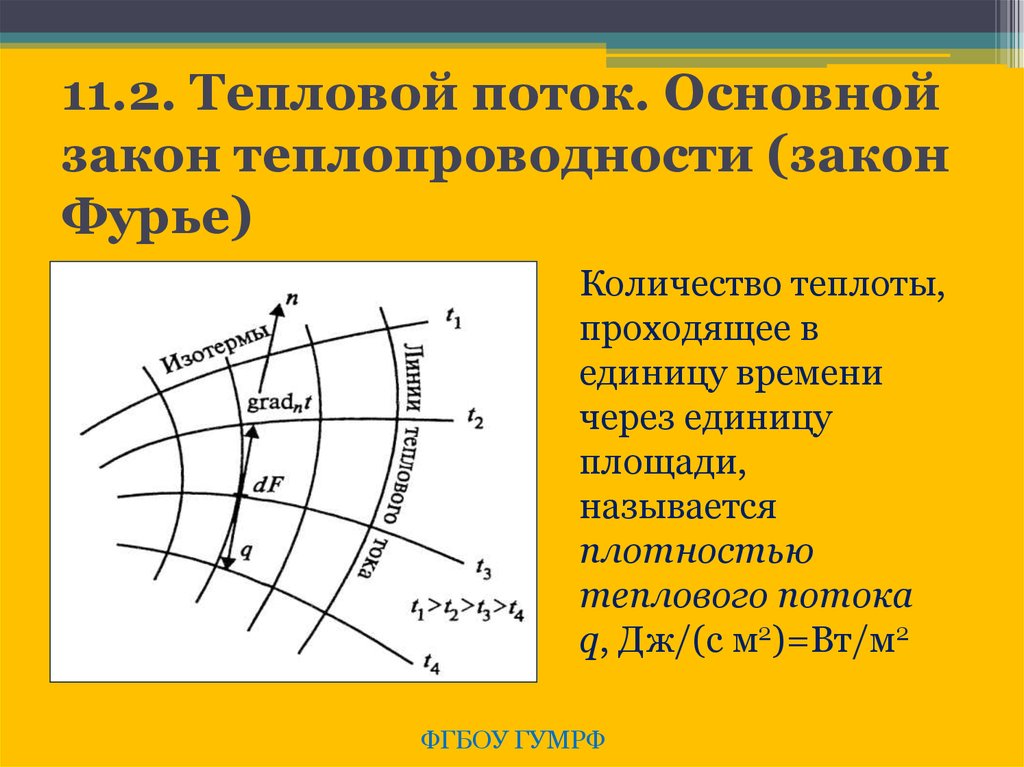
23. 11.2. Тепловой поток. Основной закон теплопроводности (закон Фурье)
Количество теплоты,проходящее в
единицу времени
через единицу
площади,
называется
плотностью
теплового потока
q, Дж/(с м2)=Вт/м2
ФГБОУ ГУМРФ
24. Тепловой поток. Основной закон теплопроводности (закон Фурье)
Величина вектораплотности теплового
потока,
перпендикулярного
элементарной
площадке dF , зависит
только от физических
свойств тела и
температурного
градиента.
ФГБОУ ГУМРФ
25. Закон Фурье
Закон Фурье:qn λgradn t λ t n
или в скалярном виде:
dt
q n λ
dn
Линии, в каждой точке
которых вектор q
направлен по
касательным к ним,
называются линиями
теплового тока.
ФГБОУ ГУМРФ
26. 11.3. Коэффициент теплопроводности
Коэффициент теплопроводности λ, Вт/(м · К)характеризует способность вещества проводить
теплоту и численно равен количеству тепла,
проходящему в единицу времени через единицу
изотермической поверхности при единичном
температурном градиенте:
λ
q
dt
dn
ФГБОУ ГУМРФ
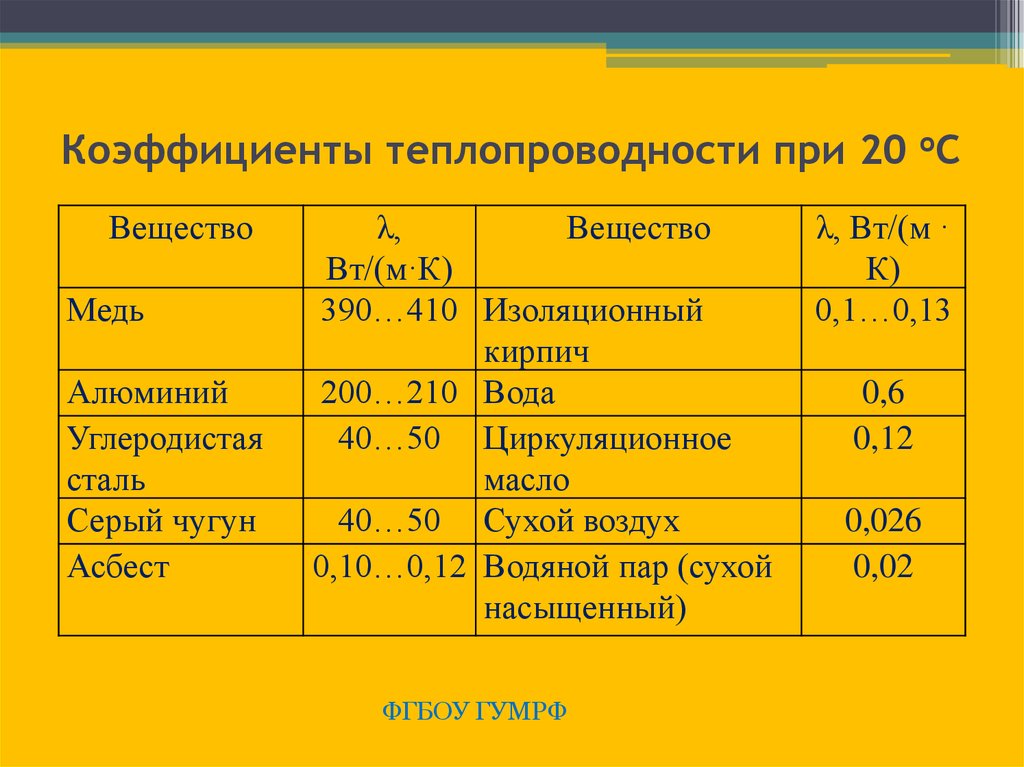
27. Коэффициенты теплопроводности при 20 оС
ВеществоМедь
Алюминий
Углеродистая
сталь
Серый чугун
Асбест
λ,
Вещество
Вт/(м·К)
390…410 Изоляционный
кирпич
200…210 Вода
40…50 Циркуляционное
масло
40…50 Сухой воздух
0,10…0,12 Водяной пар (сухой
насыщенный)
ФГБОУ ГУМРФ
λ, Вт/(м ·
К)
0,1…0,13
0,6
0,12
0,026
0,02
28. 11.4. Дифференциальное уравнение теплопроводности
dtа 2t
d
В развернутом виде:
2t 2t 2t
t
t
t
t
wx
wy
wz
а 2 2 2
x
y
z
y
z
x
В твердом теле, где перемещение вещества
отсутствует (w = 0):
2t 2t 2t
t
а 2 2 2
y
z
x
ФГБОУ ГУМРФ
29. Коэффициент температуропроводности
dtа 2t , где a
d
c
Коэффициент температуропроводности а (м2/с )
представляет собой плотность теплового потока при
единичном температурном градиенте, отнесенную к
плотности вещества и к его теплоемкости.
Коэффициент
а
пропорционален
скорости
изменения
температуры
или
скорости
распространения изотермической поверхности в теле.
При прочих равных условиях скорее нагреется или
охладится то тело, у которого больше а.
ФГБОУ ГУМРФ
30. 11.5. Условия однозначности задач теплопроводности
В теории теплопроводности существуют четыре видаусловий однозначности:
1. Геометрические условия, характеризующие форму и
размеры тела, в котором происходит процесс
распространения теплоты.
2. Физические условия, характеризующие свойства тела
(задаются λ, с, ρ, закон распределения внутренних
источников теплоты и др.).
3. Временные (начальные) условия, которые задаются
при нестационарных режимах
4. Граничные условия (ГУ), определяющие особенности
протекания теплообмена на поверхности тела.
ФГБОУ ГУМРФ
31. 11.6. Способы задания граничных условий теплообмена
В ГУ I рода задается распределение температуры наповерхности тела для каждого момента времени:
tw = t(xw, yw, zw, τ).
В ГУ II рода задаются значения плотности теплового
потока для каждой точки поверхности :
qw = q(xw, yw, zw, τ).
t
q
t
t
с
w
Граничное условие III рода : w
n w
Граничное условие IV рода определяет теплообмен в
местах контакта двух тел по закону теплопроводности:
t
t
1 w 2 w
n 1
n 2
ФГБОУ ГУМРФ
32. 11.7. Стационарная тепло-проводность через однослойную плоскую стенку
11.7. Стационарная теплопроводность через однослойнуюплоскую стенку
t
Пусть температурное поле в
стенке одномерно
d
t
t
w1
w2
и стационарно
t t
0
y z
t
0 ,
заданы ГУ I рода:
x = 0: t = tw1; x = δ: t = tw2.
0
δ
x
2
ФГБОУ ГУМРФ
33. Стационарная теплопроводность через однослойную плоскую стенку
Тогда дифференциальное уравнение теплопроводности2
d
t
такого поля примет вид:
0
dx 2
Его интегрирование дает: dt
A
dx
,
общее решение: t = Ax +B.
Подстановка в него ГУ позволяет определить постоянные
интегрирования: A t w1 t w2 , В = tw1.
d
Тогда уравнение температурного поля в стенке:
t w1 t w2
t t w1
x
d
t w1 t w2
По закону Фурье находим: q
d
ФГБОУ ГУМРФ
34. 11.8. Стационарная теплопроводность через многослойную плоскую стенку
ttw 1
d1
d
2
dn
t
w2
1
d3
t w1 t w2
d1
t t
q 2 w2 w3
d2
q 1
twtw
33
2
tw 4
3
q 3
···
tw n
n
tw (n+1)
t w3 t w4
d3
… … ….
q n
t wn t wn 1
x
3
Отсюда найдем плотность теплового потока :
ФГБОУ ГУМРФ
t w1 t w n 1
q
n d
i
i 1 i
dn
35. 11.9. Теплопроводность через цилиндрическую стенку
Из формулы Фурье тепловой потокчерез стенку длиной l на
произвольном радиусе r:
dt
dt
Q
F 2 rl
dr
dr
Разделив переменные и проинтегрировав
от r1 до r2, получим:
r
Q
ln 2 t w1 t w2
2 l r1
Откуда:
Q
ФГБОУ ГУМРФ
2 l
t t
r2 w1 w 2
ln
r1
36. Теплопроводность через цилиндрическую стенку
Величина плотности теплового потока различна дляизотермических поверхностей различного радиуса:
qr1
t w1 t w2
Q
аналогично:
2 r1l
r1 ln r2 / r1
t w1 t w2
qr2
r2 ln r2 / r1
Величина теплового потока, отнесенная к единице
длины цилиндра:
Q
2
ql
l
ln r2 / r1
t w1 t w2
называется погонной плотностью теплового потока.
Эта величина одинакова на любом радиусе от от r1 до r2.
ФГБОУ ГУМРФ
37. Решение уравнения теплопроводности
2t 2t 2tt
а 2 2 2
y
z
x
Перейдем от декартовых к цилиндрическим
координатам, учитывая, что
t t
0 , получим:
z
t
0
d 2t 1dt
0
2
dr
rdr
и
Откуда: t = Alnr + B.
ГУ: при r = r1 t = tw1; при r = r2 t = tw2.
A
Подставляя значения констант
интегрирования в общее решение :
ФГБОУ ГУМРФ
t w1 t w 2
t t
; B t w1 w1 w 2 ln r1
r
r
ln 2
ln 2
r1
r1
t t w1
t w1 t w2 r
ln
r2
r1
ln
r1
38. 11.10. Теплопроводность через многослойную цилиндрическую стенку
Погонная плотность тепловогопотока для всех слоёв одинакова:
Решение системы уравнений:
2 t w1 t w n 1
ql
r
r
1 r2 1
1
ln
ln 3 ...
ln n 1
1 r1 2 r2
n
rn
или
ql
2 t w1 t w n 1
n
1 ri 1
ln
ri
i 1 i
ФГБОУ ГУМРФ
ql 2 1
ql 2 2
t w1 t w2
r
ln 2
r1
t w 2 t w3
r
ln 3
r2
…………….
…………….
t wn t w n 1
ql 2 n
r
ln n 1
rn
39. 11.11. Нестационарная теплопроводность
2t 2t 2tt
а 2 2 2
y
z
x
В простейшем случае одномерной задачи разогрева плоской
бесконечной стенки постоянной толщины δ:
t t
0
y z
t
2t
a 2
x
Рассмотрим случай с ГУ III рода на поверхностях стенки,
определяемых интенсивностью теплоотдачи αг и αо и
температурой греющей tг и tо охлаждающей сред, и при
условии, что в начальный момент времени при τ = 0
температура стенки равна температуре холодной среды:
t(x, τ = 0) = tо
ФГБОУ ГУМРФ
40. Нестационарная теплопроводность
Решение уравнения:d x
t x, t о
d
Bi
tг tо
1 Biо о
Biг
1 Biо
i
i
2 a
Bi
sin
d
x
cos
d
x
exp
i 2
i
о
d
d
d
Biо
i2
1
i
i 1
3 cos i i sin i
Biо sin i i cos i 1
2 sin i i cos i
2
Biг
Biг
2
2
где μi — корни характеристического tg
уравнения:
d
d
Biо о ; Biг г
Biо Biг
2 Biо Biг
— числа (критерии) Био, характеризующие
интенсивность
теплообмена
среды
с
поверхностью твердого тела.
ФГБОУ ГУМРФ
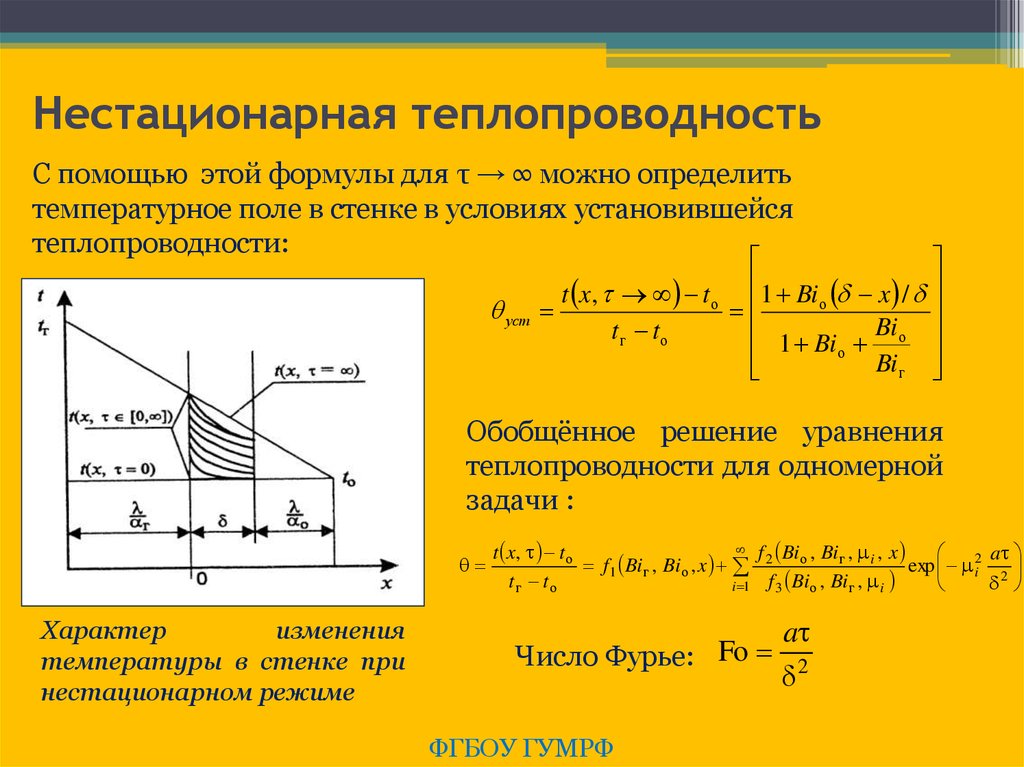
41. Нестационарная теплопроводность
С помощью этой формулы для τ → ∞ можно определитьтемпературное поле в стенке в условиях установившейся
теплопроводности:
уст
t x, tо 1 Bi о d x / d
Bi
tг tо
1 Bi о
о
Bi г
Обобщённое решение уравнения
теплопроводности для одномерной
задачи :
Характер
изменения
температуры в стенке при
нестационарном режиме
f Bi , Bi , , x
t x, t о
a
г
i
f1 Biг , Biо , x 2 о
exp i2 2
tг tо
d
i 1 f 3 Bi о , Bi г , i
Число Фурье: Fo
ФГБОУ ГУМРФ
a
d2
42. Контрольные вопросы и задания к главе 11
1. Как передается теплота в природе и технике?2. Что представляет собой теплопроводность и
как она осуществляется?
3. Что называется температурным полем и
температурным градиентом?
4. Что называется плотностью теплового потока?
5. Что и как определяет закон Фурье?
6. Что называется коэффициентом
теплопроводности? Его размерность?
7. Охарактеризовать влияние температуры на
коэффициент теплопроводности.
8. Какой вид имеет дифференциальное уравнение
теплопроводности?
ФГБОУ ГУМРФ
43. Контрольные вопросы и задания к главе 11
9. Какой вид принимает дифференциальное уравнениетеплопроводности для случая одномерной стационарной
передачи теплоты через плоскую стенку?
10. Определить краевые условия в задачах
теплопроводности.
11. Определить граничные условия в стационарных задачах
теплопроводности.
12. Как определить плотность теплового потока в случае
стационарной теплопроводности через многослойную
плоскую стенку при граничных условиях I рода?
13. Как определить погонную плотность теплового потока в
случае стационарной теплопроводности через
многослойную цилиндрическую стенку при граничных
условиях I рода?
14. Назвать особенности стационарной теплопроводности
через цилиндрическую стенку.
ФГБОУ ГУМРФ
44. Глава 12. КОНВЕКТИВНЫЙ ТЕПЛООБМЕН
12.1. Понятия и определенияКонвективным называется теплообмен между
поверхностью твердого тела и окружающей его
жидкой или газообразной средой, перемещающейся
относительно поверхности.
Закон Ньютона—Рихмана:
q tw t
где α, Вт/(м2·К), - коэффициент теплоотдачи,
tw — температура на поверхности твердого тела .
ФГБОУ ГУМРФ
45.
Понятия и определенияКоэффициент теплоотдачи α равен плотности теплового
потока при температурном напоре между поверхностью и
омывающей ее средой (tw –t) в один Кельвин.
Пограничным слоем называется
тонкий слой жидкости или
газа, в котором параметры
процесса меняются от значений
на стенке до значений в
основном потоке.
ФГБОУ ГУМРФ
46. 12.2 Дифференциальные уравнения конвективного теплообмена
12.2.1. Система уравнений движения Навье—Стокса для вязкой несжимаемой жидкости
dwx
p
g x
2 wx ;
d
x
dw y
p
g y
2 w y ;
d
y
dwz
p
2
g z
wz
d
z
где wx, wy, wx, - проекции вектора скорости на
координатные оси;
μ, Н·с/м2 — динамический коэффициент вязкости .
ФГБОУ ГУМРФ
47. Дифференциальные уравнения конвективного теплообмена
12.2.2. Уравнение сплошностиУравнение сплошности выражает закон сохранения
массы в неразрывном потоке.
wz
wx wy
0
x
y
z
Для несжимаемых жидкостей при ρ = const:
wx w y wz
0
x
y
z
Уравнение теплопроводности:
2t 2t 2t
t
t
t
t
wx
wy
wz
а 2 2 2
x
y
z
y
z
x
ФГБОУ ГУМРФ
48. Дифференциальные уравнения конвективного теплообмена:
dwxp
g x
2 wx ;
d
x
dw y
p
g y
2 w y ;
d
y
dwz
p
2
g z
wz
d
z
wz
wx wy
0
x
y
z
2t 2t 2t
t
t
t
t
wx
wy
wz
а 2 2 2
x
y
z
y
z
x
ФГБОУ ГУМРФ
49. Дифференциальные уравнения конвективного теплообмена:
12.2.3. Краевые условияКраевые условия, позволяют из бесчисленного множества
решений выделить одно, относящееся к поставленной задаче.
К ним относятся:
— геометрические, характеризующие форму и размеры
системы, в которой протекает процесс;
—
физические, определяющие физические особенности
процесса, обычно это теплофизические характеристики тела
и окружающих его сред;
— граничные, описывающие закономерности протекания
теплообмена на поверхностях тела;
— временные, характеризующие известные положения о
развитии процесса во времени.
ФГБОУ ГУМРФ
50. 12.3. Основы теории подобия
ОпределенияДва физических явления подобны, если все
характеризующие их однородные параметры в
сходственных точках пространства и в сходственные
моменты времени пропорциональны или связаны
преобразованием подобия:
φ 2(х2; τ2) = φ 2(сlх1; сττ2) = φ2(х2; τ2) = сφ φ1(х1; τ1)
где φ1, φ2 — однородные параметры подобных
процессов; сl, сτ, сφ — константы подобия.
Подобные процессы описываются одинаковыми
уравнениями и отличаются только масштабом
описывающих их величин.
ФГБОУ ГУМРФ
51. Основы теории подобия
Междуконстантами
подобия
существуют
соотношения, называемые индикаторами подобия и
определяемые физическими законами исследуемых
подобных процессов.
Эти соотношения могут быть выражены также и
непосредственно
через
сами
параметры,
характеризующие подобные процессы, и в этом
случае называются числами или критериями
подобия.
Первая теорема подобия:
Подобные процессы имеют одинаковые числа
подобия.
ФГБОУ ГУМРФ
52. Основы теории подобия
Вторая теорема подобия:Закон физического процесса может быть выражен
математической
зависимостью
между
соответствующими числами подобия.
Для того чтобы два физических процесса были
подобными,
необходимо
соблюдение
условий
геометрического,
кинематического,
временного,
температурного и физического подобия, подобия сил,
а также подобия начальных и граничных условий.
Геометрическое подобие означает подобие формы
x
y
z
и пропорциональность размеров: 2 2 2 cl const —
x1
константа геометрического подобия.
ФГБОУ ГУМРФ
y1
z1
53. Основы теории подобия
Временное подобие означает пропорциональностьвремен развития процессов: 2 c const
1
— константа временного подобия.
Кинематическое подобие подразумевает одинаковую
форму линий тока и пропорциональность скоростей:
wx 2
wx1
wy 2
wy1
wz 2
wz1
cw const
— константа скоростного подобия.
Физическое подобие означает пропорциональность
физических свойств во всех точках:
2
с
1
2
с
1
2
a2
с
сa
1
a1
ФГБОУ ГУМРФ
54. Основы теории подобия
Подобие сил означает пропорциональностьдействующих сил:
p2
fx 2
сp
сf ;
p1
fx1
Температурное подобие означает пропорциональность
температур во всех точках:
t2
сt
t1
— константа температурного подобия.
ФГБОУ ГУМРФ
55. 12.4. Числа гидромеханического подобия
How
idem
l
- число гомохронности Но представляет собой
безразмерное время развития или проявления процесса.
Обратная величина Sh l
w
— число Струхаля — показывает соотношение сил
инерции, вызванных локальными и конвективными
ускорениями.
Число Фруда Fr
gl
idem
2
w
характеризует соотношение потенциальной энергии в
поле сил тяжести и кинетической энергии в потоке.
ФГБОУ ГУМРФ
56. Числа гидромеханического подобия
pw2
показывает соотношение потенциальной энергии сил
давления и кинетической энергии.
Или в виде E p
Число Эйлера: Eu
u
w2
показывает соотношение гидравлических потерь
(перепада давления Δр) и динамического напора ρw2.
wl
Число Рейнольдса: Re=
idem
показывает соотношения сил инерции и сил вязкого
трения.
ФГБОУ ГУМРФ
57. 12.5. Числа теплового подобия
a -число Фурье представляет собой безразмерноеl 2 время развития процесса.
wl
Число Пекле Pe
a
является мерой отношения конвективного переноса
теплоты к переносу ее теплопроводностью в сжимаемой
жидкости (λж) и устанавливает подобие температурных
полей.
Fo
Число Нуссельта: Nu
αl
- основная безразмерная
ж
характеристика конвективного теплообмена.
Число Прандтля: Pr Pe v
Re
a
ФГБОУ ГУМРФ
58. Числа теплового подобия
23
gl
wl
gl
Gr Fr Re 2 0
2 t 2 t - число Грасгофа.
w v
v
Во всех числах подобия величины w и τ
—
характерная скорость и характерное время развития
процесса.
Линейная величина l называется характерным
размером.
В качестве характерного размера выбирается
размер, наиболее существенно влияющий на
распределение температур и скоростей в потоке
жидкости или газа.
ФГБОУ ГУМРФ
59. 12.5. Критериальные уравнения конвективного теплообмена
Математическая модель процесса конвективноготеплообмена может быть выражена математической
зависимостью
между
числами
теплового
и
гидромеханического подобия:
Nu = f1 (Gr, Re, Pe, l/l0) или Nu = f2 (Gr, Re, Pr, l/l0).
Nu = с Rem Prn(l/l0)p
c, n, m, p – определяются экспериментально.
Nu ж
Коэффициент теплоотдачи:
l
ФГБОУ ГУМРФ
60. 12.6. Теплообмен в свободном потоке (естественная конвекция)
Свободным называется движение жидкости илигаза в поле сил тяжести, вызванное только
разницей плотностей в частях заполняемого объема,
обусловленной неоднородностью температурного
поля. В этом случае конвекция называется
естественной.
Формула М.А. Михеева:
Nu = c (Gr Pr)n.
Около вертикальных поверхностей :
с = 0,15; n = 0,33,
для горизонтальных поверхностей : с = 0,5; n = 0,25,
если GrРr ≥ 6×1010 (развитое турбулентное течение)
ФГБОУ ГУМРФ
61. 12.7. Теплообмен в вынужденном потоке (вынужденная конвекция)
Вынужденным называется движение, созданноеспециальным
устройством
для
перемещения
жидкости или газа (насос, вентилятор и т. п.).
12.7.1. Режимы движения вязкой среды
Ламинарным называется движение, при котором
слои жидкости или газа не перемешиваются и
перемещаются
параллельно
друг
другу
Турбулентным называется движение, при котором
частицы жидкости или газа движутся хаотично и
происходит перемешивание слоев
ФГБОУ ГУМРФ
62.
Режимы движения вязкой средыРаспределение векторов скорости в вынужденных потоках
жидкости в круглой прямой трубе
а) при ламинарном движении; б) при турбулентном движении
В трубах и каналах: при числах Рейнольдса
Re < Reкр = 2300 течение ламинарное,
при Re > Reкр = 2300 — турбулентное.
ФГБОУ ГУМРФ
63.
12.7.2. Теплоотдача в каналахламинарном режиме движения
при
Формула М.А. Михеева:
Nu 0,17 Re
Pr
Prw
0,33
Gr
0,1
Pr
0, 43
0, 25
Pr
Prw
0, 25
Поправка
учитывает направление теплового потока (от стенки
к жидкости или наоборот). Температурный фактор
существен
для
жидкостей,
особенно
для
нефтепродуктов. Для воздуха и двухатомных газов
число Pr слабо зависит от температуры и эту
поправку можно считать равной 1.
ФГБОУ ГУМРФ
64.
12.7.3. Теплоотдача в каналахтурбулентном режиме движения
при
Формула М.А. Михеева:
Nu 0,021 Re
0,8
Pr
0, 43
Pr
Prw
0, 25
За характерный размер l при вынужденной
конвекции
в
круглых
трубах
принимается
внутренний диаметр.
Для труб и каналов некруглой формы за
характерный размер принимают эквивалентный
диаметр dэ:
4S
dэ
ФГБОУ ГУМРФ
65.
12.7.4. Теплоотдачаомывании гладких труб
при
поперечном
Формула А.А. Жукаускаса :
Nu с Re Pr
n
0,38
Pr
Prw
0, 25
где с = 0,5; n = 0,5
при 0 < Re < 103;
с = 0,25; n = 0,6 при
103 < Re < 2·105;
За характерный размер принят наружный диаметр трубы.
ФГБОУ ГУМРФ
66.
12.7.5. Теплоотдачаомывании пучков труб
при
поперечном
Схемы расположения труб
в коридорных (а) и
шахматных (б) пучках
труб
Nu c Re n Pr0,33 s
в коридорном пучке
с = 0,26, n = 0,65;
в шахматном пучке
с = 0,41, n = 0,6;
за характерный размер
принят наружный
диаметр трубы.
ФГБОУ ГУМРФ
67.
Теплоотдачапучков труб
при
поперечном
омывании
Nu c Re n Pr0,33 s
εs — поправочный коэффициент, учитывающий
влияние относительного расположения рядов труб:
0,15
для коридорного пучка:
s2
s
d
для шахматного пучка при
s1
2
s2
s1
2
s2
1
6
s
s 1
s2
при
εs = 1,12 .
Где s1 — поперечный шаг разбивки трубного пучка,
s2 — продольный шаг разбивки трубного пучка .
ФГБОУ ГУМРФ
68. 12.8. Конвективный теплообмен при изменении агрегатного состояния
Теплообмен при кипении жидкостиПри пузырьковом кипении различных жидкостей
(включая жидкие металлы)в условиях свободного
движения : Nu c Re n Pr0,33
При
Re
c
n
Re 10 5 10 4
≤0,01
≥0,01
0,0625
0,1250
0,50
0,65
Pr 0,86 7,6
Для давлений р = 0,2 ÷ 80 бар: α = 46 Δt2,33 p0,5,
где Δt = tw — ts , tw — температура стенки, ˚С;
ts — температура насыщения, ˚С;
p — абсолютное давление пара, бар.
ФГБОУ ГУМРФ
69. Конвективный теплообмен при изменении агрегатного состояния
Теплоотдача при конденсации параСуществуют два режима конденсации: капельная и
пленочная конденсация.
Для пленочной конденсации: Nu = f(Pr, Ga, K),
r
Где K c t — число Кутателадзе,
p к
3
gl
Ga Fr Re 2 2 — число Галилея,
v
r — скрытая теплота парообразования;
ср — теплоемкость конденсата.
ФГБОУ ГУМРФ
70. Конвективный теплообмен при изменении агрегатного состояния
Теплоотдача при конденсации параПри конденсации на вертикальных и горизонтальных
поверхностях:
3 2
Nu конд. c 4 Gaж Prж K c 4
ж ж r
ж tкl
параметры λж, ρж, μж и числа подобия определяются при температуре
1
tср t s t w
;
2
r — скрытая теплота парообразования при температуре насыщения
ts ;
Определяющим размером l является высота для вертикальных
поверхностей или наружный диаметр для горизонтальных труб;
коэффициент с = 1.13 для вертикальных поверхностей, и с = 0,72 для
горизонтальных поверхностей.
ФГБОУ ГУМРФ
71. Контрольные вопросы и задания к главе 12
1. Что называется конвективным теплообменом?2. Что называется коэффициентом теплоотдачи?
3. Написать основные уравнения конвективного
теплообмена.
4. Какие физические процессы называются
подобными?
5. Что представляют собой безразмерные
характеристики физических процессов (числа или
критерии подобия)?
6. Назвать основные числа подобия процессов
конвективного теплообмена.
ФГБОУ ГУМРФ
72. Контрольные вопросы и задания к главе 12
7. Записать критериальные уравненияконвективного теплообмена (общий вид).
8. Как изменяется интенсивность конвективного
теплообмена в зависимости от режима движения
обтекающей поверхность твердого тела жидкости
(газа)?
9. Охарактеризовать конвективный теплообмен в
условиях кипения жидкости, назвать критические
точки.
10. Охарактеризовать конвективный теплообмен в
условиях конденсации пара.
ФГБОУ ГУМРФ
73. Глава 13. ТЕПЛОПЕРЕДАЧА
Теплопередачей(или
рекуперативным
теплообменом)
называют
процесс
распространения
теплоты
от
одной
движущейся среды (теплоносителя) к другой
движущейся среде через разделяющую их
твердую стенку.
ФГБОУ ГУМРФ
74.
13.1. Теплопередача черезоднослойную и многослойную
плоские стенки
t
t
d
ж1
t
w1
t
w2
1
λw
t
w1
ж2
2
w2
По закону Ньютона-Рихмана:
q = α1(tж1 — tw1);
по закону Фурье:
t t
q w w1 w2
d
по закону Ньютона-Рихмана:
q = α2(tw2 — tж2),
откуда:
q
x
ФГБОУ ГУМРФ
tж1 tж 2
k tж1 tж 2
1
d
1
1 w 2
75.
Теплопередача через однослойную стенкуt
t
d
tж1 tж 2
q
k tж1 tж 2
1
d
1
1 w 2
ж1
t w1
1
t
w2
λw
t ж2
w1
2
w2
где:
1
1 d
1
k
2 · К)
,
Вт/(м
1 w 2
коэффициент теплопередачи.
x
Коэффициент
теплопередачи
численно
равен
количеству теплоты, которое передается через единицу
поверхности стенки в единицу времени при температурном
напоре в 1К между омывающими стенку теплоносителями.
ФГБОУ ГУМРФ
76.
Теплопередача через многослойную стенкуq
t
t
d 1 d2
2
t
w2
w1
dn
ж1
tw1
1
d3
w2
1
tw
n
2
twn+1
3
n
tж2
x
1
1
di 1
k , Вт/(м2 · К)
1 i 1 i 2
n
tw3
tw4
t ж1 t ж2
k t ж1 t ж2
d
1 d1 d 2
1
... n
1 1 2
n 2
где:
коэффициент теплопередачи.
Величина, обратная k, называется
термическим
сопротивлением
теплопередаче R, м2·К/Вт:
n d
1
1
1
i
R
k 1 i 1 i 2
ФГБОУ ГУМРФ
77.
13.2. Теплопередача черезцилиндрическую стенку
Плотность теплового потока :
qr1
Q
2 r1l
qr2
Q
2 r2l
;
Погонная плотность теплового
потока: q Q
l
l ,
откуда: ql 2 r1qr1 2 r2 qr2
где по закону Ньютона—
Рихмана:
qr1 = α1(tж1 – tw1); и
qr2 = α2(tw2 – tж2).
ФГБОУ ГУМРФ
78.
Теплопередача черезчерез цилиндрическую стенку
Откуда ql 2 r1 1 ( t ж1 tw1)
и:
ql 2 r2 2 ( t w 2 t ж2 )
Тепловой поток через твердую
стенку :
Q
2 w
ql
l
tw 1 tw2 .
ln r2 / r1
Погонная плотность теплового
потока
через
однослойную
цилиндрическую стенку:
ql
Q
2
tж1 tж 2
1
1
1
l
ln r2 / r1
1r1 w
2 r2
ФГБОУ ГУМРФ
79.
Теплопередача черезчерез цилиндрическую стенку
Или
ql k l ( t ж1 tж2 )
где k l
2
1
1
1
ln r2 / r1
1r1 w
2 r2 , Вт/(м · К)
— погонный коэффициент теплопередачи.
Для многослойной цилиндрической стенки:
1
1 ri 1
1
kl 2
ln
r
r
r
i
1
i
i
2 n 1
11
n
1
где λi — коэффициент теплопроводности i-го слоя стенки;
ri — внутренний радиус i-го слоя
ФГБОУ ГУМРФ
80.
13.3. Термическое сопротивление.Критическая толщина изоляции
Погонное термическое сопротивление Rl (м·К)/Вт :
n
1
1
ri 1
1
Rl
ln
2 1 r1 i 1 2 i
ri
2 2 rn 1
Тепловой изоляцией называют любое покрытие
теплоотдающей поверхности, которое приводит к
снижению потерь теплоты в окружающую среду.
Rl
1
1
1
r
1
r
1
ln 2
ln из
kl 2 1 r1 2 w r1 2 из r2 2 2 rиз
Критическому значению радиуса изоляции : rиз rкр
соответствует минимальное значение термического
сопротивления Rlmin .
ФГБОУ ГУМРФ
из
2
81.
Критическая толщина изоляцииКритический
радиус
изоляции зависит только
от
теплопроводящих
свойств изоляции (λиз) и
интенсивности
теплообмена на внешней
поверхности
изоляции
(α2) : rиз rкр из
2
Наложение изоляции толщиной δиз < (rкр – r2) (кривая
2) только увеличивает теплопотерю.
В случаях r2 > rкр (кривая 1) изоляция любой толщины
увеличивает общее термосопротивление .
ФГБОУ ГУМРФ
82.
Контрольные вопросы и задания кглаве 13
1.
2.
3.
4.
Какой процесс называется теплопередачей?
Что называется коэффициентом теплопередачи?
Что такое термическое сопротивление?
Как определить коэффициент теплопередачи
через плоскую многослойную стенку?
5. Как определить коэффициент теплопередачи
через многослойную цилиндрическую стенку?
6. Как определяется критический радиус изоляции
теплонесущей трубы?
ФГБОУ ГУМРФ
83. Глава 14. ЛУЧИСТЫЙ ТЕПЛООБМЕН
14.1.Основные
понятия
и
определения
Тепловое излучение представляет собой
процесс
распространения
внутренней
энергии
излучающего
тела
в
виде
электромагнитных волн. Так называют
электромагнитные возмущения, исходящие из
излучаемого тела и распространяющиеся в
вакууме со скоростью света с = 2,9979 × 108м/с.
ФГБОУ ГУМРФ
84.
Основные понятия и определенияВозбудителями электромагнитных волн являются
заряженные частицы, т. е. электроны и ионы,
входящие в состав вещества. Излучение в
диапазоне длин волн λ = 0,8…100 мкм является
тепловым.
Интенсивность излучения зависит от природы тела,
его
температуры,
длины
волны,
состояния
поверхностиа для газов — еще от толщины слоя и
давления.
С увеличением температуры тела его
энергия излучения увеличивается, так как
увеличивается внутренняя энергия вещества.
ФГБОУ ГУМРФ
85.
Основные понятия и определенияЕпогл
А
— коэффициент поглощения;
Епад
R
Еотр
— коэффициент отражения;
Епад
Епроп
D
Епад — коэффициент пропускания.
A+R+D=1
Тела, которые пропускают всю падающую на
них энергию, называются прозрачными .
Тела, у которых 0 < D ≤ 1, называют
полупрозрачными (стекло, кварц и т. п.).
ФГБОУ ГУМРФ
86.
Основные понятия и определенияПоверхность, поглощающая всю падающую на нее
лучистую энергию (Аs = 1), называется абсолютно
черной.
Поверхность, отражающая все падающие на нее
лучи (R = 1), называется абсолютно белой.
Интегральный (во всем диапазоне волн) лучистый
поток с единицы поверхности в полупространство в
единицу
времени
называется
излучательной
способностью или плотностью интегрального
излучения тела Е, Вт/м2: E dQ
dF
Интенсивность излучения Iλ,
Вт/м3:
ФГБОУ ГУМРФ
dE
I
d
87.
14.2. Основные законы тепловогоизлучения
Интенсивность излучения абсолютно черного тела
в вакуум определяется законом Планка:
5
I s
c1
c
exp 2 1
T
,
где с1 = 3,74·10 –16 Вт·м2; с2 = 1,44·10 –2 м·К —
постоянные Планка.
Длина
волны
λms
мм,
соответствующая
максимальному
значению
интенсивности
монохроматического
излучения,
при
данной
температуре подчиняется закону смещения Вина:
λms·Т = 2,9.
ФГБОУ ГУМРФ
88.
Основные законы теплового излученияT
Закон Стефана—Больцмана: Es cs
100
4
определяет интегральную плотность излучения
абсолютно черного тела в вакуум,
где cs = 5,77 Вт/(м2·К4) — коэффициент излучения
абсолютно черного тела.
Плотность интегрального излучения серого тела :
4
T
T
E c
c
s
100
100
4
где с = εсs — коэффициент излучения серого тела.
ФГБОУ ГУМРФ
89.
Основные законы теплового излученияЗакон Кирхгофа:
соотношение излучательной и поглощательной
способностей
серых
тел
при
одинаковой
температуре постоянно и равно излучательной
способности при той же температуре абсолютно
черного тела:
E/A = Es или E/Es = c/cs = ε = A.
Плотность интегрального излучения серого тела :
4
T
T
E c
c
s
100
100
4
где с = εсs — коэффициент излучения серого тела.
ФГБОУ ГУМРФ
90.
14.3. Излучение газовПлотность теплового излучения между стенкой и
проходящим около нее газом :
4
T 4
T
q w c s г г г w w
100
100
w
,
w 1
2
где
— эффективная степень черноты
стенок канала;
qг
г
— отношение количества энергии
qs
излучения газов и абсолютно черного тела
(εг — при температуре газа Тг; г w—
стенки Тw).
ФГБОУ ГУМРФ
при температуре
91.
14.4. Излучение между твердымителами
Плотность теплового излучения между
параллельными поверхностями :
T 4 T 4
q cпр 1 2
100 100
,
где индексы 1 и 2 относятся к первой и второй
поверхностям,
спр
1 1 1
c1 c2 cs
1
— приведенный коэффициент
излучения,
с1, с2 — коэффициенты излучения 1 и 2 тела
соответственно.
ФГБОУ ГУМРФ
92.
Взаимное тепловое облучение двухповерхностей
Тепловой поток между
двумя излучающими
поверхностями :
T 4 T 4
Q cпр F1 1 2
100 100 ,
где
спр
ФГБОУ ГУМРФ
1 F1 1
1
c1 F2 c2 c s
1
93.
Контрольные вопросы и задания кглаве 14
1. Какова физическая сущность лучистого
теплообмена?
2. Что представляет собой абсолютно черная
поверхность твердого тела?
3. Как определяется интегральная плотность
излучения абсолютно черной поверхности?
4. Чему равен коэффициент излучения абсолютно
черного тела (постоянная Стефана—Больцмана)?
5. Как определяется плотность интегрального
излучения серого тела?
6. Что устанавливает закон Кирхгофа?
ФГБОУ ГУМРФ
94.
Контрольные вопросы и задания кглаве 14
7. Как рассчитывается лучистый теплообмен между
стенкой и газом?
8. Как определяется эффект лучистого теплообмена
между твердыми телами?
9. Как влияют на лучистый теплообмен между
телами разделительные экраны?
ФГБОУ ГУМРФ
95. Глава 15. ОСНОВЫ РАСЧЕТА ТЕПЛООБМЕННЫХ АППАРАТОВ
15.1. Типы теплообменных аппаратовЕсли теплообмен
осуществляется
при
непосредственном
смешении
теплоносителей в теплообменнике, то
такой
теплообменник
называется
смесительными.
ФГБОУ ГУМРФ
96.
Типы теплообменных аппаратовЕсли теплообмен осуществляется в
условии периодически меняющегося
протока
теплоносителя
и
теплоприемника в одном попеременно
нагреваемом и охлаждаемом канале, то
такие
теплообменники
называются
регенеративными.
В рекуперативных теплообменниках
обменивающиеся
теплотой
среды
разделены стенкой.
ФГБОУ ГУМРФ
97.
15.2. Основы расчетарекуперативного теплообменника
Тепловой баланс
Тепловая мощность теплообменника:
tгор
Gхол cхол t хол
t хол
Q Gгорcгор tгор
С другой стороны:
Q kF tср
или Q lkl t ср
—
, Вт
для
цилиндрических
теплообменных поверхностей,
где F — суммарная площадь поверхности;
l — суммарная длина теплообменных элементов.
ФГБОУ ГУМРФ
98.
Основы расчета рекуперативноготеплообменника
Среднелогарифмический перепад
температур
Для прямотока: tср
t хол
t гор
t хол
t гор
ln
для противотока: t ср
t хол
t гор
t хол
t гор
t хол
t гор
t хол
t гор
ln
t хол
t гор
t хол
t гор
где t' , t" - температуры сред на входе и выходе из
теплообменного аппарата, соответственно.
ФГБОУ ГУМРФ
99.
Контрольные вопросы и задания кглаве 15
1. Что называется рекуперативным
теплообменом?
2. Как выбрать формулу для расчета числа
Нуссельта для теплоносителя, движущегося
внутри труб?
3. Какой теплообменник называется
регенеративным?
4. Как определить среднелогарифмический
перепад температур в теплообменнике?
ФГБОУ ГУМРФ
100.
Овсянников МихаилКонстантинович
доктор технических наук, профессор;
Орлова Елена Геннадьевна
кандидат технических наук, доцент;
Костылев Иван Иванович
доктор технических наук, профессор
кафедры
«Теплотехника, судовые котлы и
вспомогательные установки»
«ГУМРФ имени адмирала С. О. Макарова»
ФГБОУ ГУМРФ

































































































 Физика
Физика








