Электростатика и постоянный ток

1. ФИЗИКА

Лекция № 3
Электростатика и постоянный ток

2. Электростатика

Это раздел электродинамики,
в котором изучается
взаимодействие неподвижных
электрических зарядов.
2

3.

Электрический заряд –
это физическая величина, определяющая интенсивность
электромагнитного взаимодействия заряженных тел.
[q] = A c = Кл
Заряд любого тела дискретен и кратен элементарному
заряду:
19
e 1,6 10
Заряд протона
Кл
qp = e, заряд электрона qe = – e.
Электрон ( др.греч. ἤλεκτρον ) – янтарь.
Процесс сообщения телу электрического заряда –
электризация – состоит в перераспределении
подвижных электрических зарядов между
взаимодействующими телами.
Если Np
= Ne, то тело электрически нейтрально, q = 0.
Если Np > Ne, то заряд тела q > 0.
Если Np < Ne, то заряд тела q < 0.
3

4.

В изолированной (замкнутой) системе нет обмена зарядами с
внешними телами. Заряды лишь перераспределяются между телами
системы или смещаются в пределах одного тела.
Закон сохранения электрического заряда:
алгебраическая сумма электрических зарядов
замкнутой системы есть величина постоянная
N
qi const
i 1
Электрический заряд обладает свойством инвариантности:
величина заряда не изменяется при переходе от одной
инерциальной системы отсчета к другой.
4

5.

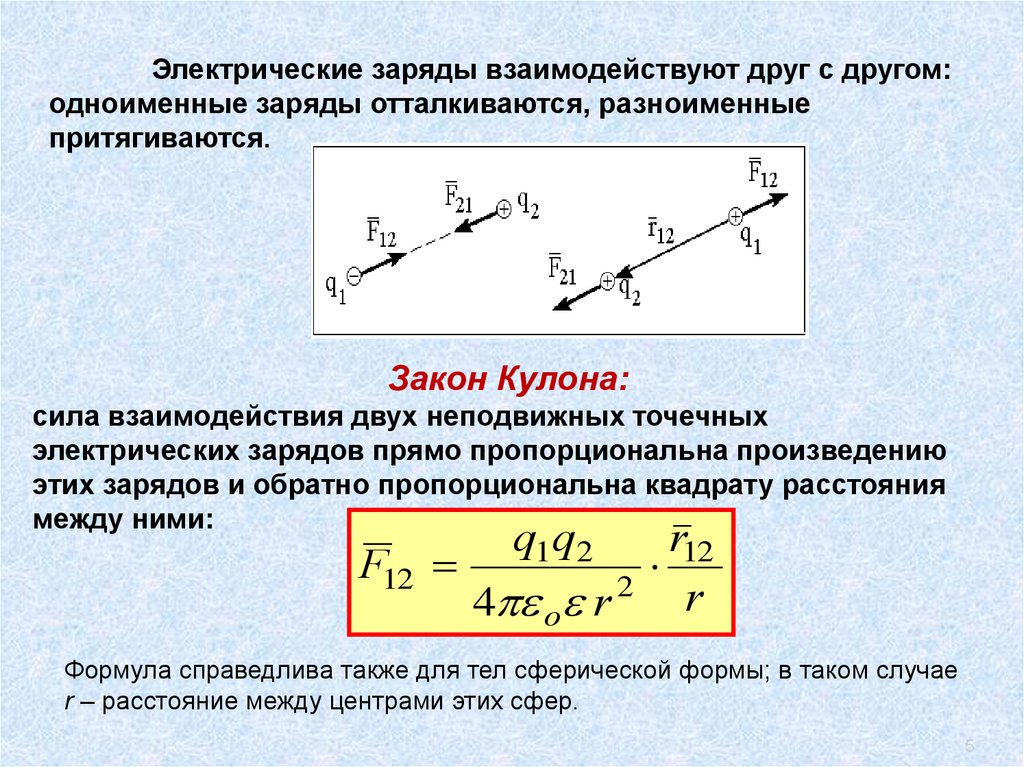
Электрические заряды взаимодействуют друг с другом:
одноименные заряды отталкиваются, разноименные
притягиваются.
Закон Кулона:
сила взаимодействия двух неподвижных точечных
электрических зарядов прямо пропорциональна произведению
этих зарядов и обратно пропорциональна квадрату расстояния
между ними:
q1q2
r12
F12
2
r
4 o r
Формула справедлива также для тел сферической формы; в таком случае
r – расстояние между центрами этих сфер.
5

6.

.
o 8,85 10
12
Ф /м
– электрическая постоянная;
– диэлектрическая проницаемость среды между зарядами.
Величина показывает, во сколько раз сила F
взаимодействия зарядов в данной среде меньше
силы Fo их взаимодействия в вакууме:
Fo
F
Взаимодействие электрически заряженных тел
осуществляется посредством электрического поля..
6

7.

Электрическое поле – одна из форм материи,
осуществляющая взаимодействие между заряженными телами.
Поле неподвижного заряда называется электростатическим.
Источники электрического поля:
электрические заряды;
переменное магнитное поле.
Наличие электрического поля проявляется в его силовом
воздействии на электрический заряд.
Напряженностью электрического поля
называется векторная величина, равная
отношению силы, действующей на
положительный пробный заряд,
помещенный в данную точку поля, к
величине этого заряда
F
E
qo
[E] = Н/Кл = В/м
7

8.

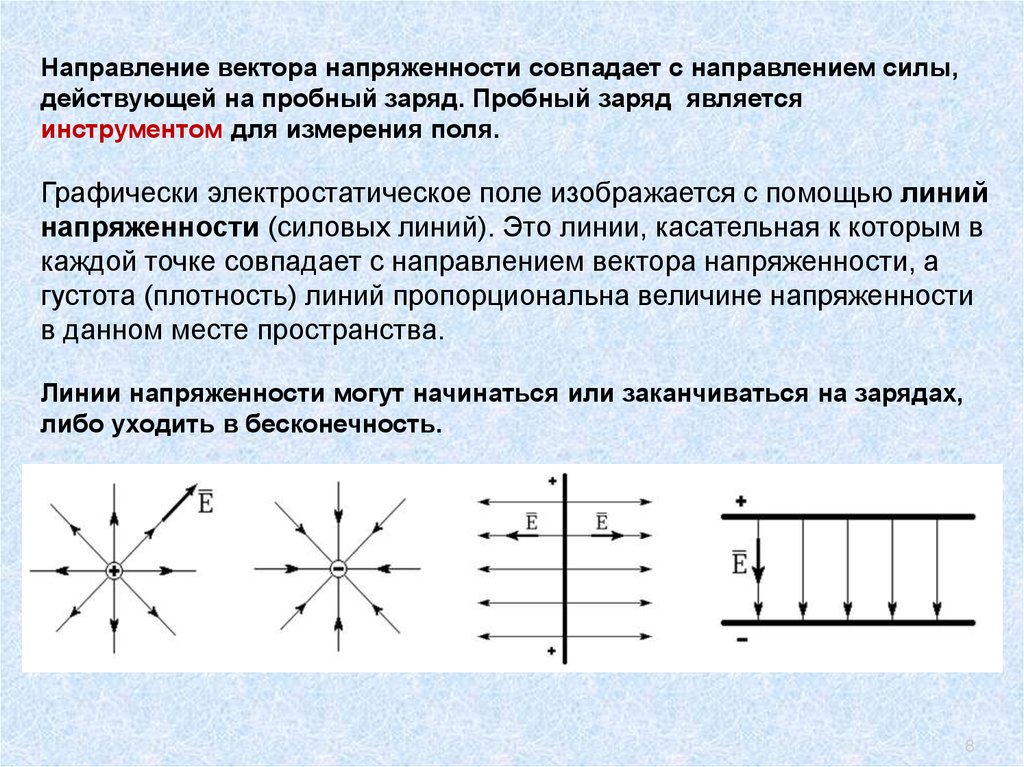
Направление вектора напряженности совпадает с направлением силы,
действующей на пробный заряд. Пробный заряд является
инструментом для измерения поля.
Графически электростатическое поле изображается с помощью линий
напряженности (силовых линий). Это линии, касательная к которым в
каждой точке совпадает с направлением вектора напряженности, а
густота (плотность) линий пропорциональна величине напряженности
в данном месте пространства.
Линии напряженности могут начинаться или заканчиваться на зарядах,
либо уходить в бесконечность.
8

9.

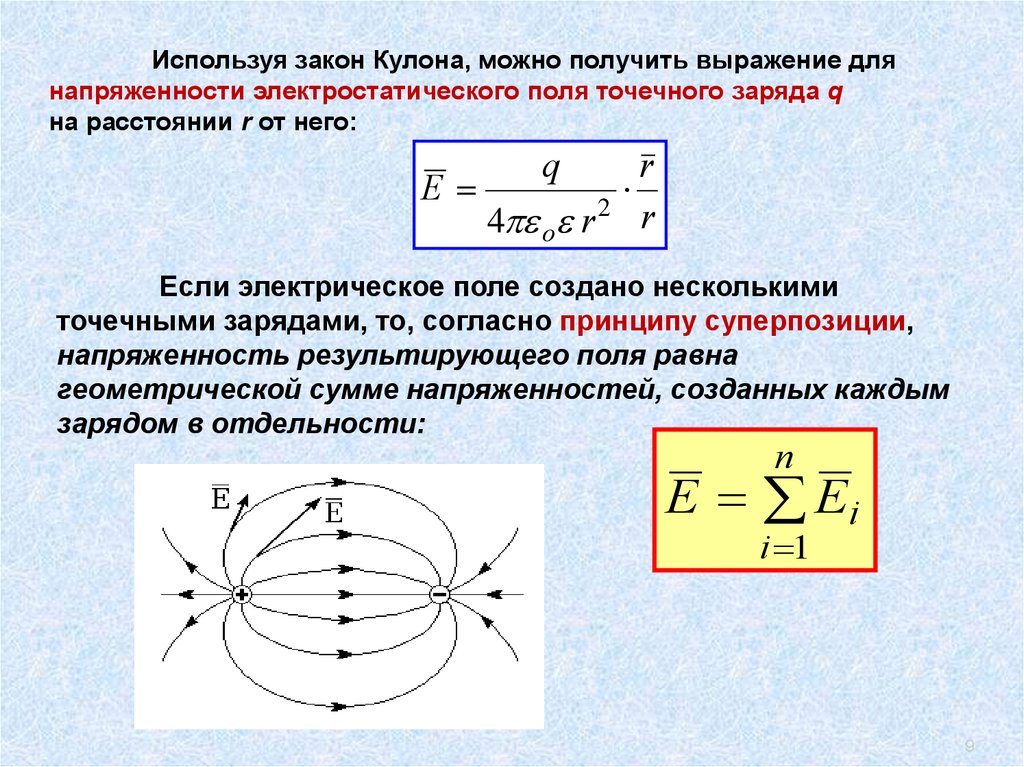
Используя закон Кулона, можно получить выражение для
напряженности электростатического поля точечного заряда q
на расстоянии r от него:
q
r
E
2 r
4 o r
Если электрическое поле создано несколькими
точечными зарядами, то, согласно принципу суперпозиции,
напряженность результирующего поля равна
геометрической сумме напряженностей, созданных каждым
зарядом в отдельности:
n
E Ei
i 1
9

10.

Потоком вектора напряженности через элементарную
площадку dS называется скалярная величина dФ, равная
скалярному произведению вектора напряженности
электрического поля на единичный вектор нормали к этой
площадке, умноженному на площадь dS
d (E dS ) (E n ) dS E dS cos En dS
Величина dФ пропорциональна числу силовых
линий, пронизывающих площадку dS.
Поток через поверхность S
конечных размеров
En dS
S
10

11.

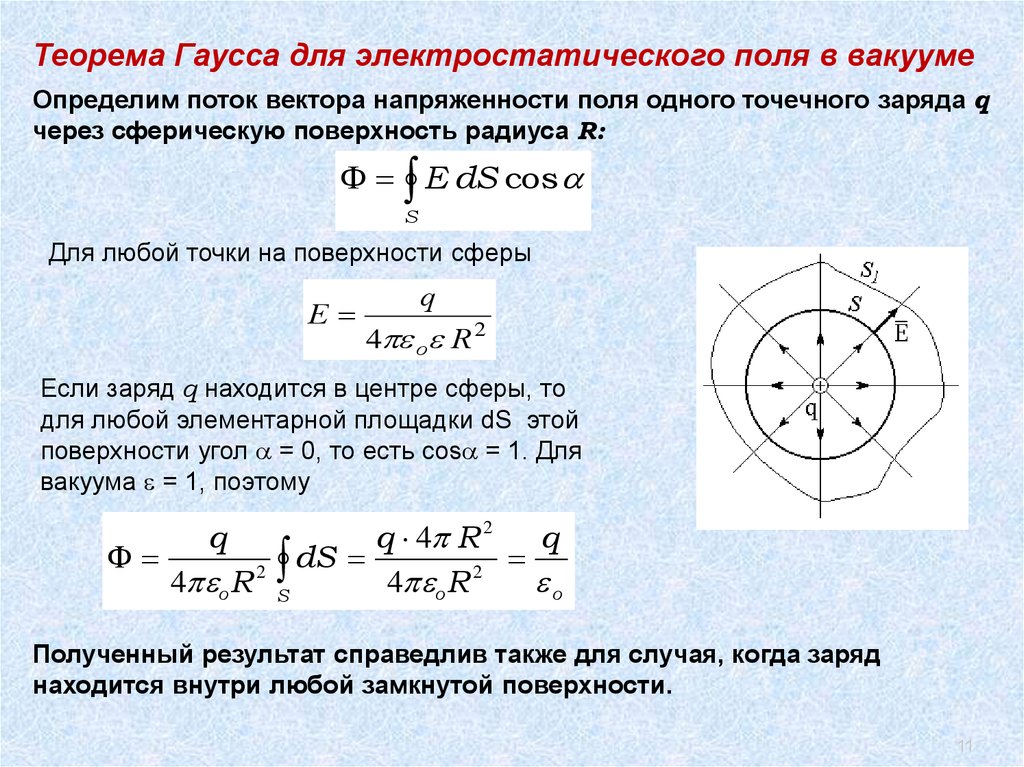
Теорема Гаусса для электростатического поля в вакууме
Определим поток вектора напряженности поля одного точечного заряда q
через сферическую поверхность радиуса R:
E dS cos
S
Для любой точки на поверхности сферы
E
q
4 o R 2
Если заряд q находится в центре сферы, то
для любой элементарной площадки dS этой
поверхности угол = 0, то есть cos = 1. Для
вакуума = 1, поэтому
q 4 R 2
q
dS
4 o R 2 S
4 o R 2
o
q
Полученный результат справедлив также для случая, когда заряд
находится внутри любой замкнутой поверхности.
11

12.

Рассмотрим наиболее общий случай: замкнутая поверхность
произвольной формы окружает несколько зарядов. Согласно
принципу суперпозиции напряженность результирующего поля
n
n
n
E dS ( Ei ) dS Ei dS
S
S
i 1
i 1 S
1
o
i 1
qi
o
n
внутри
q
i
i 1
Это теорема Гаусса для электростатического
поля в вакууме:
поток вектора напряженности электростатического поля в
вакууме через произвольную замкнутую поверхность равен
алгебраической сумме зарядов внутри этой поверхности,
деленной на электрическую постоянную о.
Если заряд находится вне замкнутой поверхности, то поток вектора Е через
нее равен нулю.
12

13.

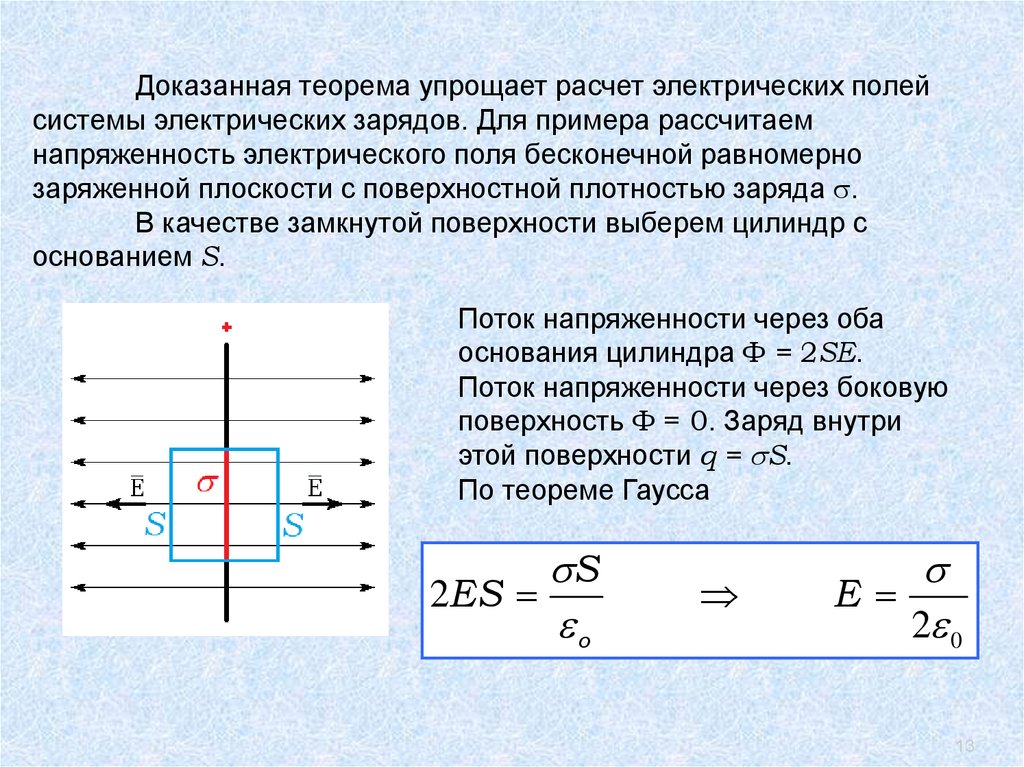
Доказанная теорема упрощает расчет электрических полей
системы электрических зарядов. Для примера рассчитаем
напряженность электрического поля бесконечной равномерно
заряженной плоскости с поверхностной плотностью заряда .
В качестве замкнутой поверхности выберем цилиндр с
основанием S.
Поток напряженности через оба
основания цилиндра Ф = 2SE.
Поток напряженности через боковую
поверхность Ф = 0. Заряд внутри
этой поверхности q = S.
По теореме Гаусса
S
2ES
o
E
2 0
13

14.

Работа электростатического поля
Пусть поле создано неподвижным точечным зарядом q.
Работа поля на элементарном участке dl траектории равна
A F dl Fdl cos
qqo
4 o r
dl cos
2
qqo
4 o r
2
dr
Работа поля вдоль всей траектории движения
A12
r2
qqo r2 dr
qqo 1
1
A
(
)
2
4 o r1 r
4 o r1 r2
r1
Работа не зависит от формы траектории и определяется только
положением начальной и конечной точки, поэтому
электростатическое поле точечного заряда потенциально, а
электростатические силы консервативны.
14

15.

[
Известно, что работа консервативной силы равна убыли
потенциальной энергии:
A12 W p ( W p 2 W p1 ) W p1 W p 2
qqo
qqo
4 o r1 4 o r2
Потенциальная энергия взаимодействия точечных зарядов
qqo
Wp
4 o r
Отношение Wp/qo является энергетической
характеристикой электростатического поля,
которая называется потенциалом
Wp
[ ] = Дж/Кл = В
qo
Потенциал – это скалярная величина, равная
потенциальной энергии единичного положительного
заряда, помещенного в данную точку
электростатического поля.
15

16.

Выражение для работы можно обобщить на случай любого
электростатического поля:
A12 F dl qo E dl
L
Величина
L
E dl называется циркуляцией вектора вдоль траектории L.
L
A12
E dl q
o
L
Циркуляция вектора напряженности равна работе сил поля по перемещению
единичного положительного заряда вдоль данной траектории.
Если траектория замкнута, то r1 r2 и тогда
A 0
L
E dl 0
L
Циркуляция напряженности электростатического поля вдоль
произвольного замкнутого контура L равна нулю.
Это положение справедливо только для электростатического поля.
Это выражение является математическим критерием потенциальности
поля.
16

17.

Потенциал поля точечного заряда q на расстоянии r от него
q
4 o r
Работа, совершаемая силами электростатического поля
при перемещении точечного заряда q из точки с
потенциалом 1 в точку с потенциалом 2
A12 W p q ( 1 2 ) q
17

18.

.
Связь между напряженностью и потенциалом
Работа сил электростатического поля при бесконечно малом
перемещении dx
A qo E x dx
Ту же работу можно выразить через потенциал:
A q o d
qo E x dx qo d
Повторив аналогичные действия для осей OY и OZ, получим
E (
i
j
k ) grad
x
y
z
Напряженность электростатического поля равна
градиенту потенциала, взятому со знаком минус.
Вектор градиента направлен в сторону наибольшего возрастания
потенциала, а вектор напряженности – в противоположную сторону.
18

19.

Графически электростатическое поле изображается не только с
помощью линий напряженности, но с использованием
эквипотенциальных поверхностей – совокупности точек с
одинаковым потенциалом.
Вектор напряженности Е в каждой точке направлен по нормали
к эквипотенциальной поверхности в сторону уменьшения
потенциала.
Густота эквипотенциальных поверхностей пропорциональна величине
и направлении напряженности в разных точках.
На рисунке пунктирными линиями показаны сечения
эквипотенциальных поверхностей плоскостью чертежа.
19

20.

Электроемкость
Потенциал уединенного проводника пропорционален его
заряду и зависит только от формы и размеров проводника:
q
C
где С – называется электроемкостью или емкостью проводника.
Величина С зависит от размеров и формы проводника,
но не зависит от заряда. Емкость Земного шара С 700 мкФ.
Конденсатором называется система двух проводников,
разноименно заряженных равными по модулю
зарядами.
Заряд конденсатора прямо пропорционален разности потенциалов его
обкладок:
q C( 1 2 ) CU
20

21.

Ёмкость плоского конденсатора
C
o S
d
где S – площадь обкладки; d – расстояние между обкладками.
При параллельном соединении n конденсаторов
n
q qi
i 1
n
C Ci
i 1
При последовательном соединении n конденсаторов
n
U U i
i 1
n 1
1
C i 1 Ci
21

22.

Энергия электростатического поля
Энергия заряженного проводника – это потенциальная энергия
взаимодействия зарядов проводника. Сообщение проводнику заряда
связано с совершением работы по преодолению электростатических сил
отталкивания между одноименными зарядами.
Процесс заряжания конденсатора можно представить, как перенос заряда
с одной обкладки на другую. При переносе заряда dq с обкладки 2 на
обкладку 1 внешние силы совершают работу
q dq
A ( 1 2 )dq Udq
C
Работа внешних сил при увеличении заряда от нуля до q
q
q dq
q2
A
2C
0 C
Энергия электрического поля заряженного конденсатора
q2
CU 2
qU
We
2C
2
2
22

23.

Энергию конденсатора можно рассматривать как энергию
электростатического поля всех зарядов конденсатора.
Выразим данную энергию через величину, характеризующую само
электрическое поле – через напряженность.
CU 2 o S ( Ed )2 o E 2V
We
2
2d
2
U Ed
V Sd
Плотность энергии электрического поля
We o E
we
V
2
2
Носителем энергии является поле.
Это выражение справедливо и для переменного электрического поля, в
котором поле существует независимо от зарядов.
23

24.

Диэлектрики в
электрическом поле
При внесении вещества в электромагнитное поле
наблюдается воздействие на заряды и магнитные
моменты молекул вещества. Смысл воздействия
поля на вещество – это ориентирующее действие
на дипольные и магнитные моменты..

25.

Электрическим диполем называется система двух
разноименных одинаковых по модулю электрических
зарядов, расположенным на расстоянии l друг от друга.
Дипольным моментом называется вектор
pe ql
где вектор l проведен от отрицательного заряда к
положительному заряду.
25

26.

Все вещества по их электрическим свойствам
можно разделить на проводники, полупроводники и
диэлектрики.
Диэлектрики – это вещества, которые не
проводят электрический ток. В диэлектриках
практически отсутствуют свободные заряды.
Диэлектрики бывают неполярные, полярные и
сегнетоэлектрики.
26

27.

Неполярные диэлектрики состоят из
симметричных молекул, в которых «центры
тяжести» положительных и отрицательных
зарядов совпадают (l = 0) (H2, N2, O2, CO2).
Собственный дипольный момент молекул
неполярных диэлектриков равен нулю.
Во внешнем электрическом поле происходит
смещение зарядов (деформация молекулы), и
молекула приобретает дипольный момент,
ориентированный по полю.
Величина смещения зарядов зависит от упругих
свойств заряда в молекуле.
27

28.

Полярные диэлектрики состоят из молекул,
которые имеют отличный от нуля собственный
дипольный момент
(H2O, NH3, HCl и др.).
До внесения в поле эти моменты ориентированы
хаотично, что поддерживается тепловым движением.
При внесении полярного диэлектрика в
электрическое поле возникает преимущественная
ориентация диполей по направлению поля, но
тепловое движение мешает этому процессу.
С увеличением температуры поляризация
уменьшается.
28

29.

Количественной мерой поляризации любого диэлектрика
является вектор поляризованности
P lim
V 0
pei
V
V
где суммируются все дипольные моменты молекул в объеме V.
Поляризованность – это электрический (дипольный)
момент единицы объема.
При внесении диэлектрика во внешнее электростатическое
поле напряженностью Ео вследствие поляризации внутри
диэлектрика образуется поле связанных зарядов
напряженностью Е , которое направлено навстречу внешнему
полю Ео.
Согласно принципу суперпозиции напряженность поля в
диэлектрике
E E0 E
29

30.

.
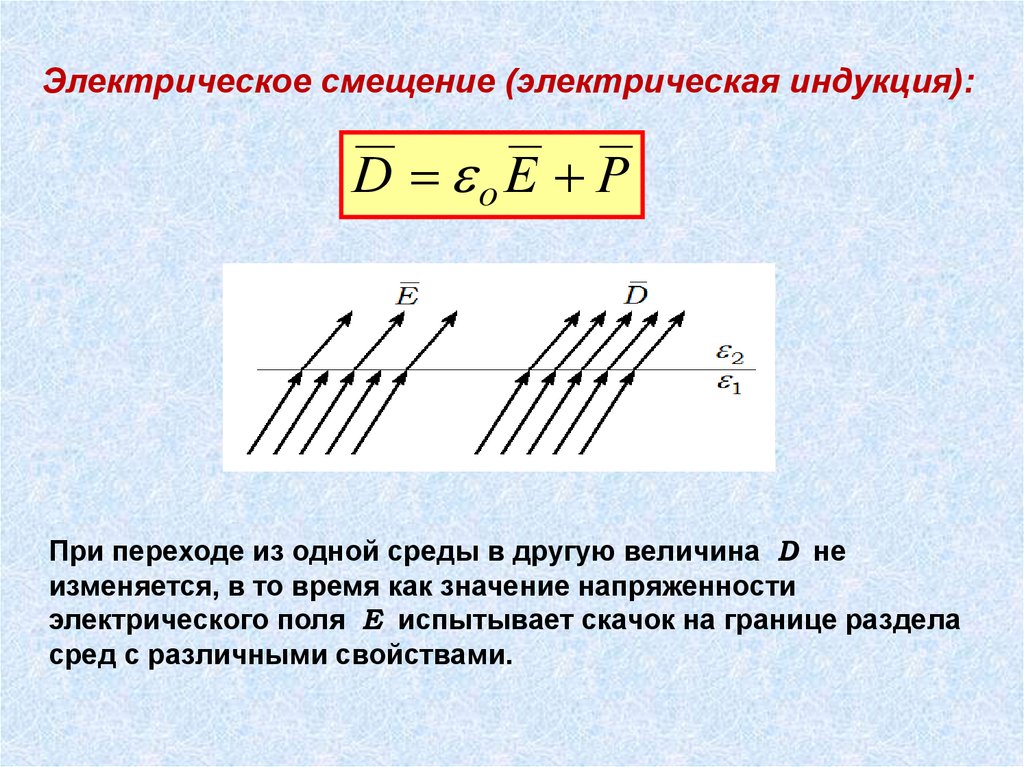
Электрическое смещение (электрическая индукция):
D oE P
При переходе из одной среды в другую величина D не
изменяется, в то время как значение напряженности
электрического поля Е испытывает скачок на границе раздела
сред с различными свойствами.

31.

Поляризованность пропорциональна напряженности внешнего
поля
P o E
Безразмерная величина называется электрической
восприимчивостью, она показывает, насколько вещество
воспринимает поле.
D o E
где величина
1 называется диэлектрической
проницаемостью.
Величины , и Р являются характеристиками вещества.
Вектор D - это характеристика источника
электрического поля, которым являются свободные
заряды.

32.

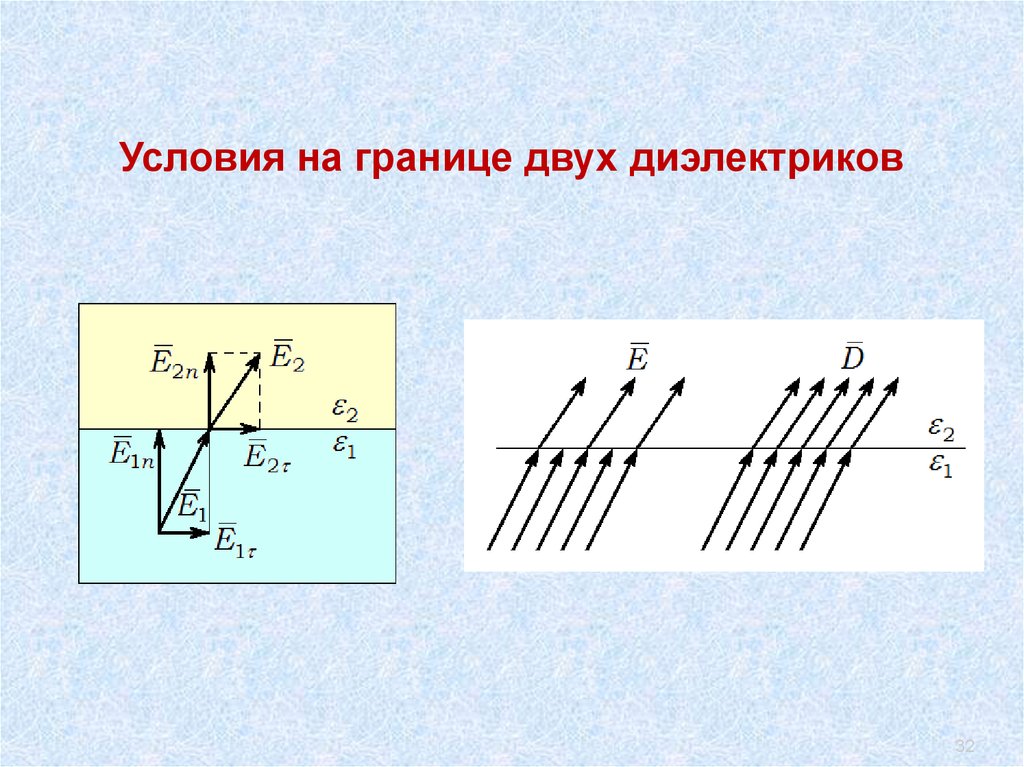
Условия на границе двух диэлектриков
32

33.

Для вакуума
E (E , dS )
S
1
o
n
внутри
q
i
i 1
где суммируются все свободные заряды в объеме, ограниченном
замкнутой поверхностью S. Других зарядов в вакууме просто нет.
Вектор D от свойств среды не зависит, следовательно, он
описывает электростатическое поле, созданное свободными
зарядами, но при таком их расположении, которое устанавливается
при наличии диэлектрика.
Основное уравнение электростатики в веществе
n
своб .
(
D
,
d
S
)
q
i
S
i 1
Поток вектора смещения электростатического поля в
диэлектрике через произвольную замкнутую поверхность
равен алгебраической сумме свободных зарядов внутри этой
поверхности.

34.

СЕГНЕТОЭЛЕКТРИКИ
- это кристаллические диэлектрики, обладающие спонтанной
(самопроизвольной) поляризованностью в определенном
интервале температуры. (Сегнетова соль, титанат бария и др.)
Сегнетоэлектрики имеют следующие отличительные свойства.
1. Большие значения диэлектрической проницаемости.
Например, для титаната бария ~ 104.
2. Нелинейный характер зависимости диэлектрической
проницаемости от напряженности электрического поля.
3. Наличие гистерезиса, т.е. зависимости поляризованности от
предыстории образца.
34

35.

4. Доменная структура: существуют макроскопические области, в
пределах которых наблюдается одинаковая спонтанная
ориентация дипольных молекул вещества.
Поляризация сегнетоэлектриков во внешнем поле заключается:
в смещении границ доменов и росте размеров тех
доменов, моменты которых близки по направлению к
направлению внешнего поля;
в повороте моментов доменов по полю.
5. Наличие так называемой точки Кюри – критической
температуры, выше которой сегнетоэлектрические свойства
исчезают, и вещество переходит в полярный диэлектрик.
Например, для сегнетовой соли сегнетоэлектрические свойства
проявляются в температурном интервале Т = (255…297) К.
Сегнетоэлектрики используются, в частности, для изготовления
конденсаторов малых размеров, но большой электроемкости.
А также для модуляции частоты электромагнитных колебаний.
35

36. Постоянный электрический ток

36

37.

Электрическим током называется
упорядоченное движение заряженных
частиц.
За направление электрического тока принято
направление движения положительного
заряда.
Различают ток проводимости и конвекционный ток.
Конвекционным током называется движение
заряженного макроскопического тела.
37

38.

[
Током проводимости называется упорядоченное
движение свободных зарядов.
Свободные заряды способны перемещаться на
любые расстояния в пределах проводника.
Необходимыми и достаточными условиями
существования тока проводимости являются:
наличие свободных зарядов;
наличие силы, действующей на свободные заряды
в определенном направлении. (Чаще всего, источником
такой силы является электрическое поле.)
38

39.

Количественной характеристикой электрического
тока является сила тока, которая равна заряду,
переносимому через рассматриваемую
поверхность за единицу времени:
dq
I
dt
[I ] = А = Кл/с
Если сила тока и его направление не изменяются с
течением времени, то электрический ток называется
постоянным.
39

40.

Плотности тока – это отношение силы тока dI
через элементарную площадку dS ,
перпендикулярную направлению тока, к ее
площади
dI
j
dS
Направление вектора j совпадает с направлением
движения зарядов в данной точке.
40

41.

.
Сила тока через поверхность S конечных размеров
I j dS j cos dS jn dS
S
S
S
- угол между направлением тока через элементарную
площадку dS и нормалью к ней;
jn- проекция вектора плотности тока на нормаль к
площадке dS.
Сила тока проводимости через поверхность S равна
потоку плотности тока через эту поверхность.
41

42.

Пусть через площадку dS за время dt переносится заряд
dq qn dV qn u dt dS
q – заряд носителя тока;
n – концентрация носителей тока;
dV – элементарный объем.
dI
j
qn u
dS
Так как векторы j и u совпадают по направлению, то
плотность тока проводимости
j qn u
(*)
u - скорость дрейфа.
42

43.

Классическая электронная теория
электропроводности металлов
В классической теории (Друде-Лоренца) электроны
проводимости рассматриваются как электронный газ,
обладающий свойствами идеального одноатомного
газа.
В отсутствии электрического поля электроны
проводимости хаотически движутся и сталкиваются с
ионами металла, которые совершают беспорядочные
тепловые колебания в узлах кристаллической решетки.
Считается, что средняя длина свободного пробега
электронов имеет порядок расстояния между узлами
кристаллической решетки.
43

44.

В присутствии электрического поля электроны
наряду с тепловым движением приобретают
некоторую скорость упорядоченного движения в
направлении, противоположном вектору
напряженности.
Считается, что при столкновении с ионами
электроны полностью теряют свою скорость
упорядоченного движения. Это означает, что
электрон движется ускоренно лишь на длине
свободного пробега, стартуя всякий раз после
столкновения с ионом от нулевой скорости.
Так как средняя длина свободного пробега
электрона мала, то средняя скорость упорядоченного
движения электронов много меньше их средней
скорости теплового движения:
u vТ
44

45.

Закон Видемана-Франца
Для металлов отношение коэффициента теплопроводности к
удельной электрической проводимости пропорционально
температуре Т :
LT
где L = 2,47 10–8 Вт Ом/К2 – постоянная Лоренца.
Взаимная связь электрической проводимости и теплопроводности
объясняется тем, что оба эти свойства металлов, в основном, обусловлены
движением свободных электронов.
Коэффициент теплопроводности увеличивается пропорционально
средней скорости частиц, так как ускоряется перенос энергии.
Электропроводность, наоборот, падает, потому что соударения при
большой скорости частиц значительно затрудняют перенос энергии.
Закон Видемана-Франца стал триумфом теории свободных электронов.
45

46.

Закон Ома в дифференциальной форме
Уравнение движения электронов на длине свободного пробега
mo
dv
eE
dt
На этом участке электроны движутся равноускоренно, поэтому
u v
1
2
v max
Интегрируя по времени в пределах от 0 до средней
продолжительности свободного пробега , получим
u
eE
2m0
eE l
2m0 vT
Подставив это в выражение (*) для плотности тока, получим
j
ne 2 l
2mo vT
E
46

47.

Величину называют удельной электропроводностью
ne 2 l
2mo vT
а величину = 1/ - удельным сопротивлением.
Закон Ома в дифференциальной форме:
j E
1
E
плотность тока проводимости равна произведению
удельной электропроводности проводника на
напряженность электрического поля в проводнике.
47

48.

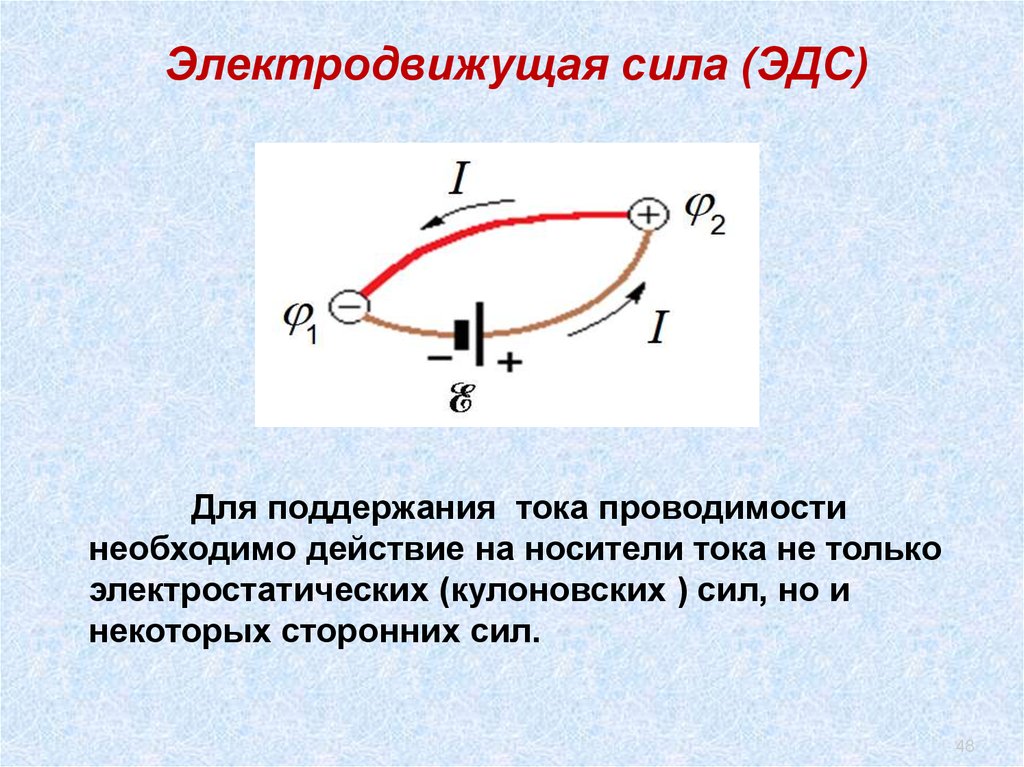
Электродвижущая сила (ЭДС)
Для поддержания тока проводимости
необходимо действие на носители тока не только
электростатических (кулоновских ) сил, но и
некоторых сторонних сил.
48

49.

Под действием сторонних сил носители тока
внутри источника тока движутся против сил
электростатического поля, так что на концах внешней
цепи поддерживается постоянная разность
потенциалов, и в цепи длительное время течет
электрический ток.
Такие силы действуют в гальванических
элементах, аккумуляторах, генераторах и т.п.
49

50.

Перемещая заряды, сторонние силы совершают работу
за счет энергии источника тока. В генераторах – это
механическая энергия, в гальванических элементах – это
энергия химических реакций на электродах.
Электродвижущая сила (ЭДС)
равна работе сторонних сил по перемещению
единичного положительного заряда
A
E
q
стор
[E ] = Дж/Кл = В
50

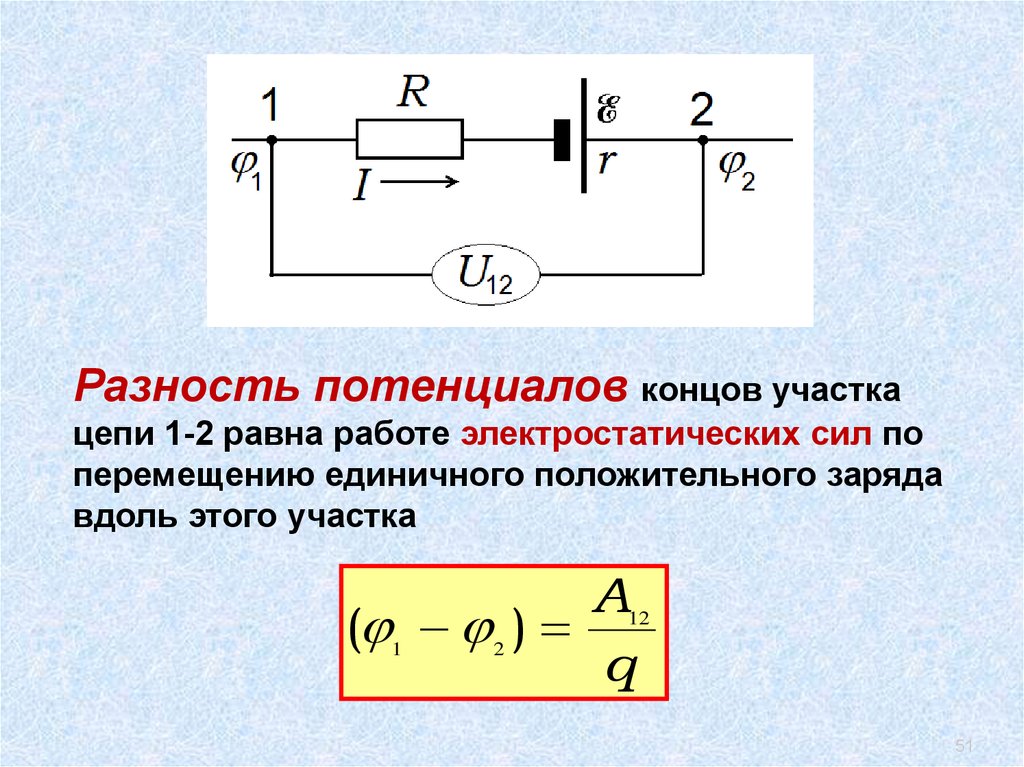
51.

Разность потенциалов концов участка
цепи 1-2 равна работе электростатических сил по
перемещению единичного положительного заряда
вдоль этого участка
А
( )
q
12
1
2
51

52.

.
Напряжением на участке цепи 1-2 называется
величина, равная суммарной работе
электростатических и сторонних сил
по перемещению единичного положительного заряда
из точки 1 в точку 2:
U ( ) E
12
1
2
[U ] = Дж/Кл = В
52

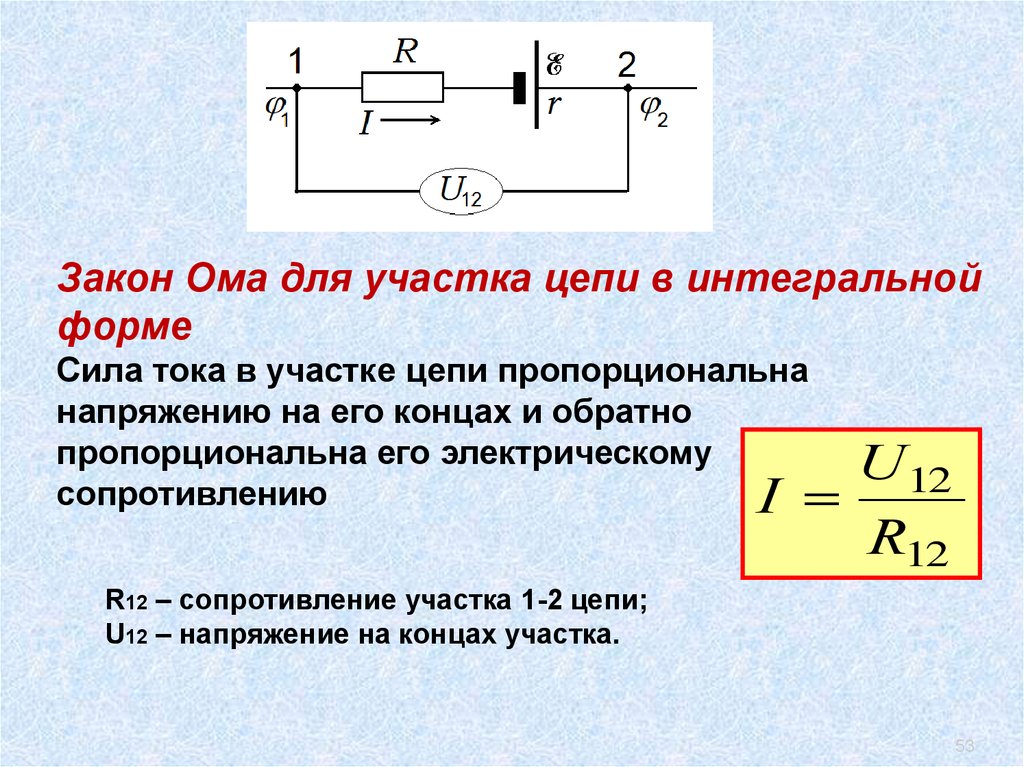
53.

Закон Ома для участка цепи в интегральной
форме
Сила тока в участке цепи пропорциональна
напряжению на его концах и обратно
пропорциональна его электрическому
сопротивлению
I
U 12
R12
R12 – сопротивление участка 1-2 цепи;
U12 – напряжение на концах участка.
53

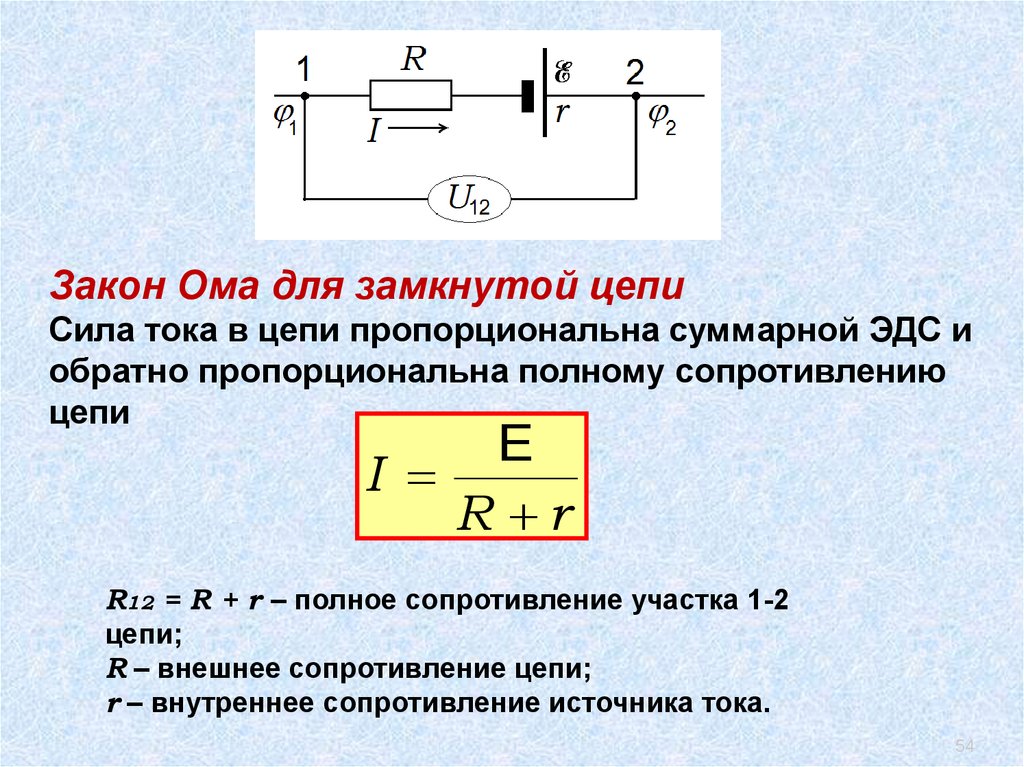
54.

Закон Ома для замкнутой цепи
Сила тока в цепи пропорциональна суммарной ЭДС и
обратно пропорциональна полному сопротивлению
цепи
E
I
R r
R12 = R + r – полное сопротивление участка 1-2
цепи;
R – внешнее сопротивление цепи;
r – внутреннее сопротивление источника тока.
54

55.

Сопротивление – способность
проводника препятствовать протеканию
электрического тока.
Сопротивление однородного проводника постоянного сечения
l
R
S
l – длина проводника; S – площадь его поперечного сечения;
– удельное электрическое сопротивление, зависящее от
материала и температуры:
(1 t )
0
о – удельное сопротивление при t = 0 С;
- температурный коэффициент сопротивления материала.
55

56.

Работа электрического тока
Умножив напряжение U12 на величину заряда dq,
прошедшего за время dt по цепи, получим элементарную работу
по перемещению этого заряда вдоль участка 1-2:
A U dq U Idt R I dt
2
12
12
12
12
За конечное время t работа тока
t
A A I R t IUt U t /R
2
12
2
12
12
0
Если постоянный электрический ток течет в цепи, состоящей из
неподвижных проводников, то эта работа тока целиком
расходуется на нагревание проводника: Q
Мощность тока
A
= A12.
U
P
IU I R
dt
R
2
2
12
12
56

57.

Литература
1. Хавруняк В. Г. Курс физики. - М.: НИЦ ИНФРА-
М, 2014. - 400 с. - ЭБС "Знаниум".
2. Рогачев Н. М. Курс физики. - М.: Лань, 2010. 448 с. . - ЭБС "Лань".
3. Трофимова Т.И. Курс физики.- М. : Академия,
2010. - 560 с.
4. «Физика. Лабораторный практикум» . - ЭБС
«ВГЛТУ»
- «Магнетизм» 5.3 (27)
- «Колебания и волны» 6.2 (30) и 6.5 (32)
- «Волновая оптика» 7.1 (35)
57

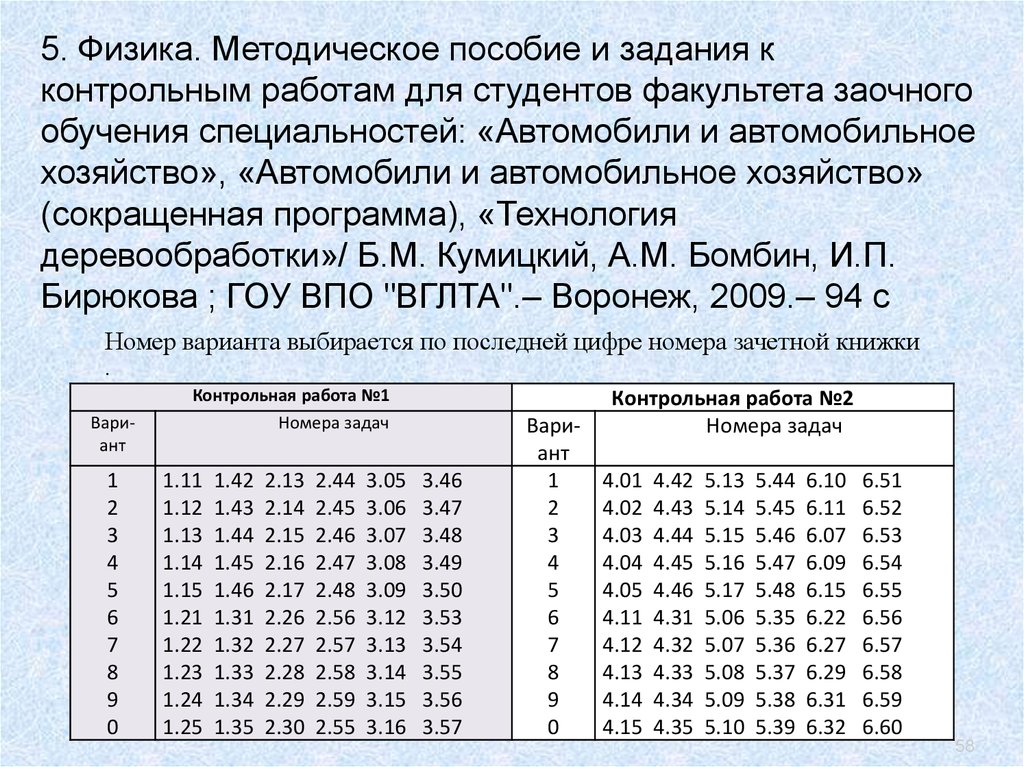
58.

5. Физика. Методическое пособие и задания к
контрольным работам для студентов факультета заочного
обучения специальностей: «Автомобили и автомобильное
хозяйство», «Автомобили и автомобильное хозяйство»
(сокращенная программа), «Технология
деревообработки»/ Б.М. Кумицкий, А.М. Бомбин, И.П.
Бирюкова ; ГОУ ВПО "ВГЛТА".– Воронеж, 2009.– 94 с
Номер варианта выбирается по последней цифре номера зачетной книжки
.
Вариант
1
2
3
4
5
6
7
8
9
0
Контрольная работа №1
Номера задач
1.11
1.12
1.13
1.14
1.15
1.21
1.22
1.23
1.24
1.25
1.42
1.43
1.44
1.45
1.46
1.31
1.32
1.33
1.34
1.35
2.13
2.14
2.15
2.16
2.17
2.26
2.27
2.28
2.29
2.30
2.44
2.45
2.46
2.47
2.48
2.56
2.57
2.58
2.59
2.55
3.05
3.06
3.07
3.08
3.09
3.12
3.13
3.14
3.15
3.16
3.46
3.47
3.48
3.49
3.50
3.53
3.54
3.55
3.56
3.57
Вариант
1
2
3
4
5
6
7
8
9
0
Контрольная работа №2
Номера задач
4.01
4.02
4.03
4.04
4.05
4.11
4.12
4.13
4.14
4.15
4.42
4.43
4.44
4.45
4.46
4.31
4.32
4.33
4.34
4.35
5.13
5.14
5.15
5.16
5.17
5.06
5.07
5.08
5.09
5.10
5.44
5.45
5.46
5.47
5.48
5.35
5.36
5.37
5.38
5.39
6.10
6.11
6.07
6.09
6.15
6.22
6.27
6.29
6.31
6.32
6.51
6.52
6.53
6.54
6.55
6.56
6.57
6.58
6.59
6.60
58

59.

Лекция окончена