Многоповерхностная теория пластичности с одной активной поверхностью

1. Многоповерхностная теория пластичности с одной активной поверхностью

И.Н. Изотов , Б.Е. Мельников, С.Г. Семенов
24 – 30 августа 2011
Нижний Новгород

2. План доклада

• Эксперименты на никелевых образцах
• Тензорная форма записи уравнений
теории
• Термодинамический анализ
• Численная реализация
• Эксперименты на стальных образцах
• Расчеты элементов конструкций
• Заключение
2/24

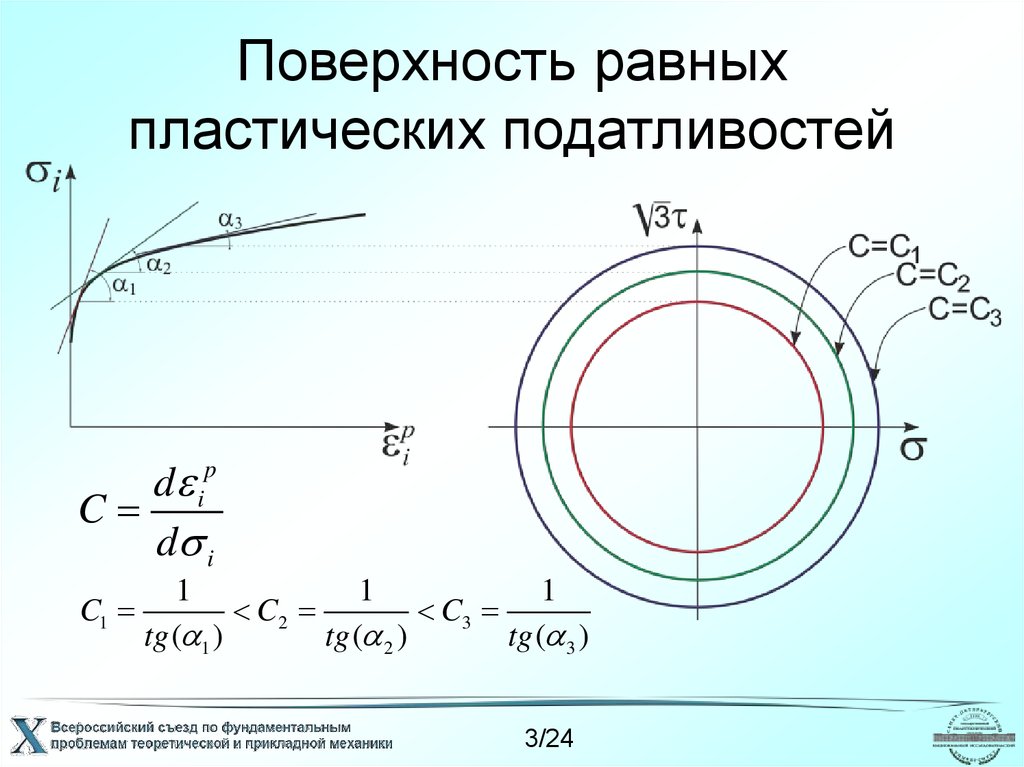
3. Поверхность равных пластических податливостей

d i
C
d i
p
C1
1
1
1
C2
C3
tg ( 1 )
tg ( 2 )
tg ( 3 )
3/24

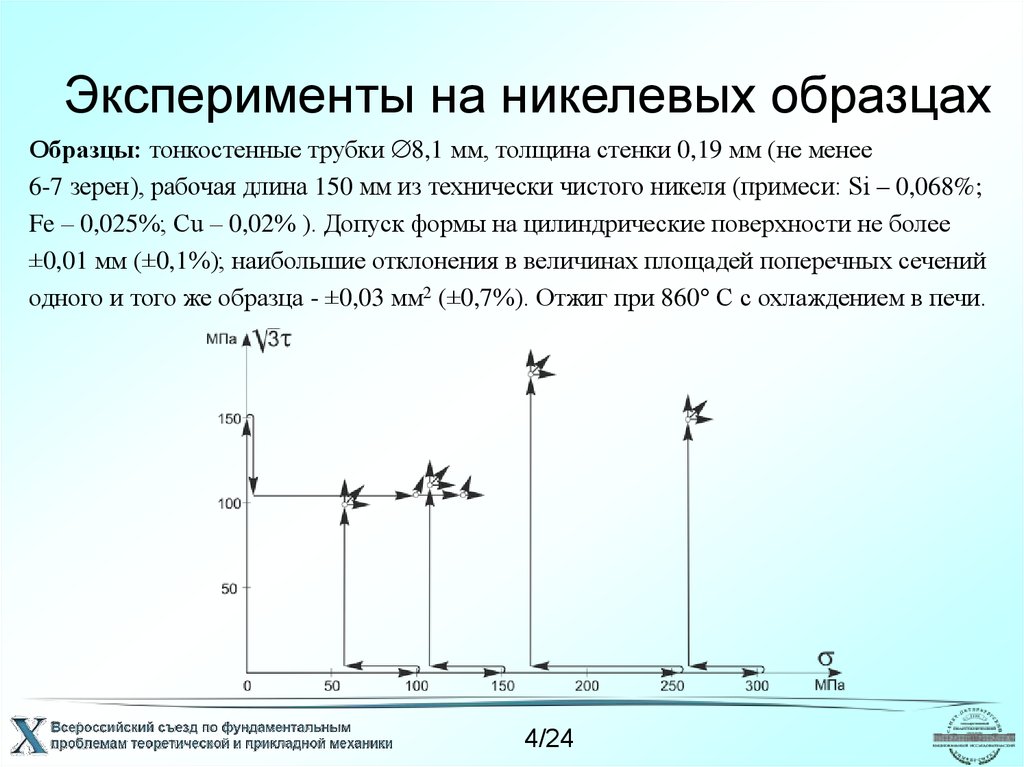
4. Эксперименты на никелевых образцах

Образцы: тонкостенные трубки 8,1 мм, толщина стенки 0,19 мм (не менее
6-7 зерен), рабочая длина 150 мм из технически чистого никеля (примеси: Si – 0,068%;
Fe – 0,025%; Сu – 0,02% ). Допуск формы на цилиндрические поверхности не более
±0,01 мм (±0,1%); наибольшие отклонения в величинах площадей поперечных сечений
одного и того же образца - ±0,03 мм2 (±0,7%). Отжиг при 860 С с охлаждением в печи.
4/24

5.

И.Н. Изотов, Ю.И. Ягн. Изучение пластического деформирования металла с деформационной
анизотропией, созданной в процессе предварительного нагружения. ДАН СССР. 1961. Т. 139, №3.
I Всесоюзный съезд по теоретической и прикладной механике 1960 г.
1. Уравнения эволюции поверхности нагружения сложны, что затрудняет их
использование в инженерной практике.
2. Геометрические места равных пластических податливостей близки к окружностям
A 0
h i0
А 0
3
h 3 i0
5/24
R B
h ak
D B
i0 B
k 1

6. Эксперименты на никелевых образцах (поле пластических податливостей)

E1
C
E3
Э
cos
3
1 2
Э
3
2
arctg
3
1
3 3
(1)
(2)
2 3 2
arctg
6/24
3
(3)
(4)

7. Погрешности эксперимента

Величина
Среднеквадратичная
абсолютная погрешность υ
Среднеквадратичная
относительная погрешность δ
δε
0,0002% < vε< 0,0003%
δε<0,3%
δγ
0,00021% < vγ < 0,00038%
δγ <0,3%
σ
max vσ≈ 0,8МПа
max δσ≈0,25%
τ
max vτ≈ 0,6МПа
max δτ≈0,28%
|δΣ|
vδS = 0,08МПа
δδS = 0,8%
|δЭ|
vδЭ≈0,0003%
max δδЭ=5%
α
0,00026%
0,0003%
V2
Э
Э
β
Max vβ ≈ 0,4˚
При |δΣ|=10 МПа, С=10-11Па-1 (С наименьшее используемое)
С
vh= 0,6·10-13Па
δh=6%
При С=10-10Па-1
vh= 1,25·10-12 Па-1
δh=1,25%
7/24

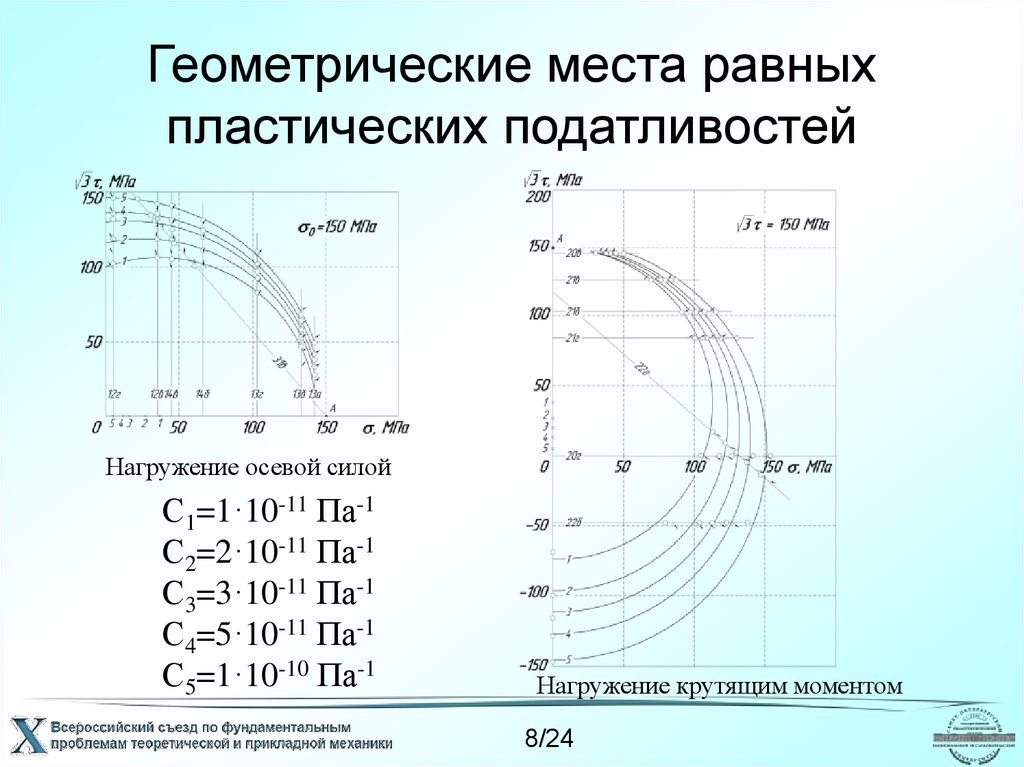
8. Геометрические места равных пластических податливостей

Нагружение осевой силой
С1=1·10-11 Па-1
С2=2·10-11 Па-1
С3=3·10-11 Па-1
С4=5·10-11 Па-1
С5=1·10-10 Па-1
Нагружение крутящим моментом
8/24

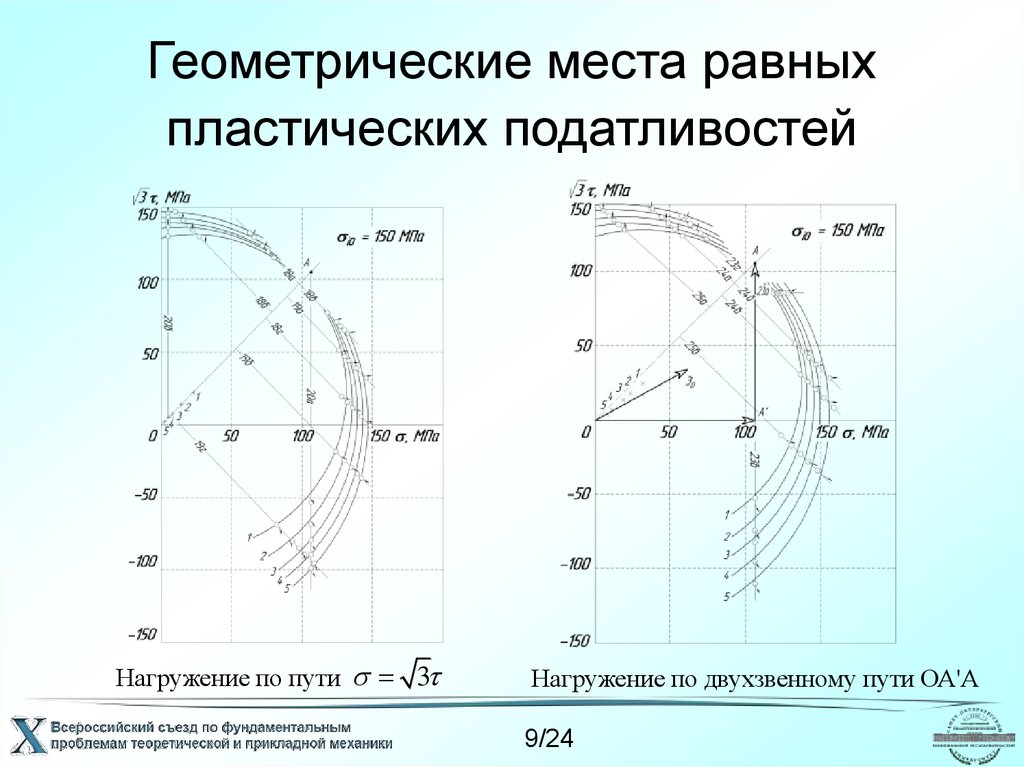
9. Геометрические места равных пластических податливостей

Нагружение по пути 3
Нагружение по двухзвенному пути ОА'А
9/24

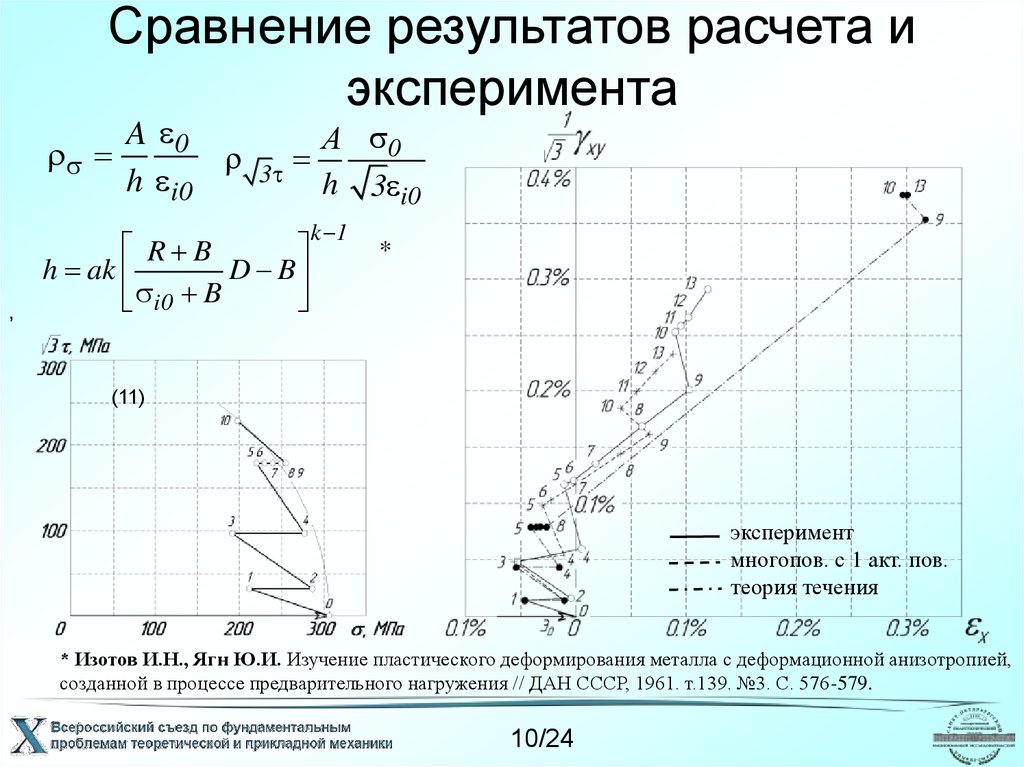
10. Сравнение результатов расчета и эксперимента

A 0
h i0
,
А 0
3
h 3 i0
R B
h ak
D B
i0 B
k 1
*
(11)
эксперимент
многопов. с 1 акт. пов.
теория течения
* Изотов И.Н., Ягн Ю.И. Изучение пластического деформирования металла с деформационной анизотропией,
созданной в процессе предварительного нагружения // ДАН СССР, 1961. т.139. №3. С. 576-579.
10/24

11. Тензорная форма записи

f k (σ σOk )
Условие возникновения нового k-го реверса
σ
dσ 0
(1)
где σ Ok - центр k-ой поверхности равных податливостей
Уравнение активной (k+1) поверхности равных пластических податливостей
Fk 1 (σ A σ R j ε p ) f k 1 (σ A) Yk 1 (σ R j p ) 0
j 1 k
(2)
где σ A σ σ Ok 1 - тензор активных напряжений, σ R j - напряжение реверса
Определяющее уравнение для пластической деформации
dε p C
f k 1 (σ A) f k 1 (σ A)
dσ
σ
σ
где С – модуль пластической податливости
11/24
(3)

12.

При использовании гиперсферы Мизеса f (σ A) f (s A) (3 2s A s A) :
dε p 3 2 C
s As A ds
s A s A
(2)
sOj 1 sOj a j (s R j sO j )
aj
(1)
(s R j 1 s R j 2 sO j ) (s R j 1 s R j )
2 (s R j sO j ) (s R j 1 s R j )
(3)
(4)
j 1 k
Уравнение поверхности
Радиус j-ых поверхностей
(пассивных)
Радиус k+1-ой поверхности
(активной)
Условие вложенности
Fk 1
3
2
s Ak 1 s Ak 1 Yk 1 0
Yk 1 3 k 1
2
(5)
j S Pj S Pj S R SO S R SO
j
j
j
j
(6)
k 1 S Ak 1 S Ak 1 S SO S SO
k 1
k 1
(7)
0 k 1 k ... 2 1
(8)
12/24

13.

Модули пластической податливости
C j C j (s A sR j 1 )
C1
d i
d i
p
k 1
C
C
k 1 1
1
N
j 2...k 1
(1)
Обращенная форма записи для МКЭ
dσ Dep dε
f (σ A ) f (σ A )
D
ep
σ
σ D
D D 1 f (σ A)
f (σ A )
D
C
σ
σ
D s A s A D
D D 2s A s A
s A D s A
3C
ep
13/24
(2)

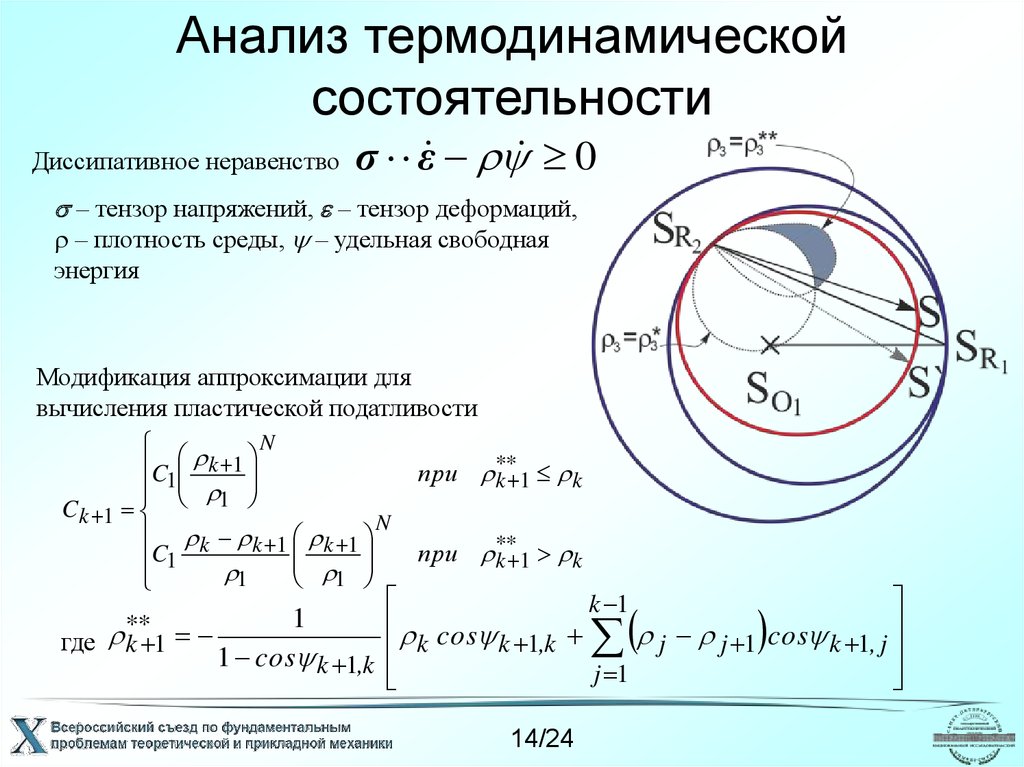
14. Анализ термодинамической состоятельности

Диссипативное неравенство
σ ε 0
– тензор напряжений, – тензор деформаций,
– плотность среды, – удельная свободная
энергия
Модификация аппроксимации для
вычисления пластической податливости
N
**
k
1
C1
при
k 1
k
1
Ck 1
N
k k 1 k 1
при *k* 1 k
C1
1
1
**
где k 1
k 1
1
cos
j j 1 cos k 1, j
k
k
1
,
k
1 cos k 1,k
j
1
14/24

15. Численная реализация

При наличии k реверсной истории на текущем шаге возможны 2k+3 ситуации:
• отсутствие возникновения и вычеркивания реверсов;
• рождение нового k+1 реверса;
• k случаев одновременного вычеркивания от одного до k реверсов;
• k+1 случая возникновения k+1-го реверса с последующим вычеркиванием от
одного до k+1 реверсов
Для учета этих особенностей шаги по напряжениям разбиваются на подшаги:
i
s
s
sl
2
2
2
(
)
s
(
)
s
sl sOk 1 i
sl sOk 1 i
Rk 1 i
l
i
s s
s s
s s
Rk 1 i (s Rk 1 i sOk 1 i ) (s Rk 1 i sOk 1 i )
i
l 1
где
l (sl sO ) (sl sO )
k 1 i
k 1 i
15/24

16.

Аналогичные выражения в пространстве деформаций для удобства реализации в МКЭ
i
i
el 1 el e
ep
i
i 1
i
i 1
sl 1 sl 1 Di 1 (el 1 el 1)
si 1 Diep 1 e
i
i 1
ep
i
i 1
sl 1 sl 1 ( )Di 1 e
i
i
i 1
i 1
sl 1 sl s
i 1
i 1
i 1
i 1
(
)
(
)
Rk 1 i l
s
s
s
s
s
s
l
O
l
O
i
k 1 i
k 1 i
i 1
i 1
i 1
i 1
i 1
i 1
s s
s s
s s
2
2
1
(s Ok 1 s l ) Dep
0 e
e D D e
ep
0
ep
0
16/24
2
2

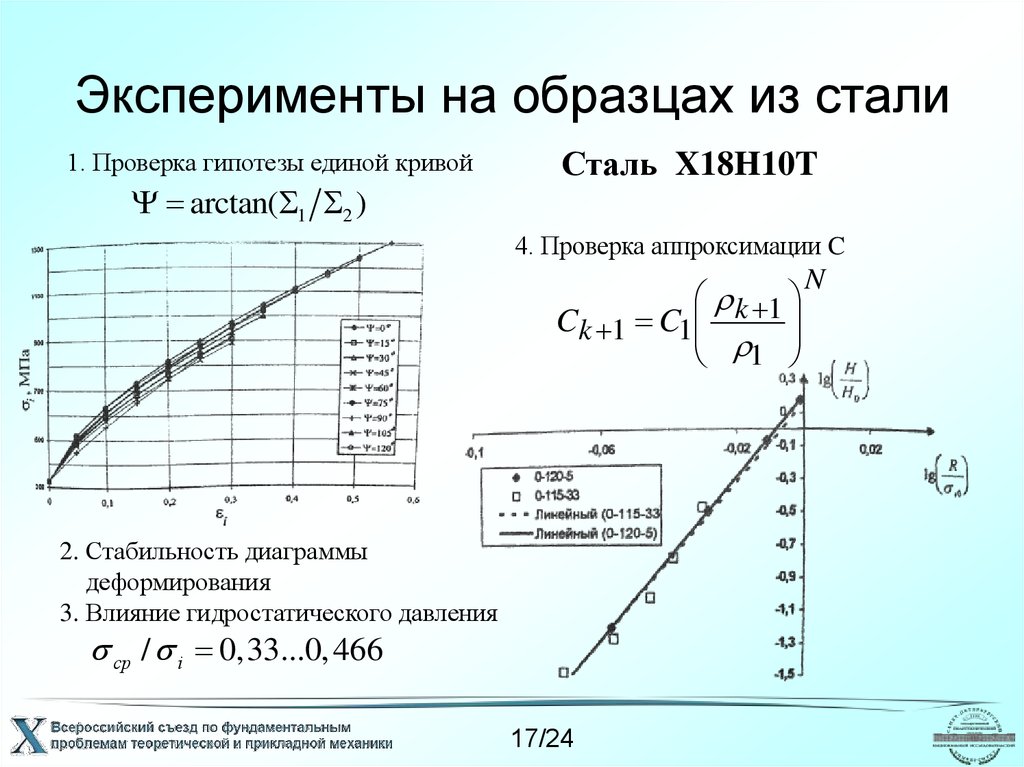
17. Эксперименты на образцах из стали

1. Проверка гипотезы единой кривой
arctan( 1 2 )
Сталь X18H10T
4. Проверка аппроксимации C
k 1
Ck 1 C1
1
2. Стабильность диаграммы
деформирования
3. Влияние гидростатического давления
ср / i 0,33...0, 466
17/24
N

18. Эксперименты на образцах из стали

18/24

19. Эксперименты на образцах из стали

Сталь SS type 304
N. S. Ottosen. Nonlinear KinematicHardening under Non-Proportional Loading.
Risø National Laboratory, DK-4000 Roskilde, Denmark July 1979
L. Szabo
1984
19/24

20. Конечно-элементный анализ

Internet: www.pantocrator.narod.ru
20/24

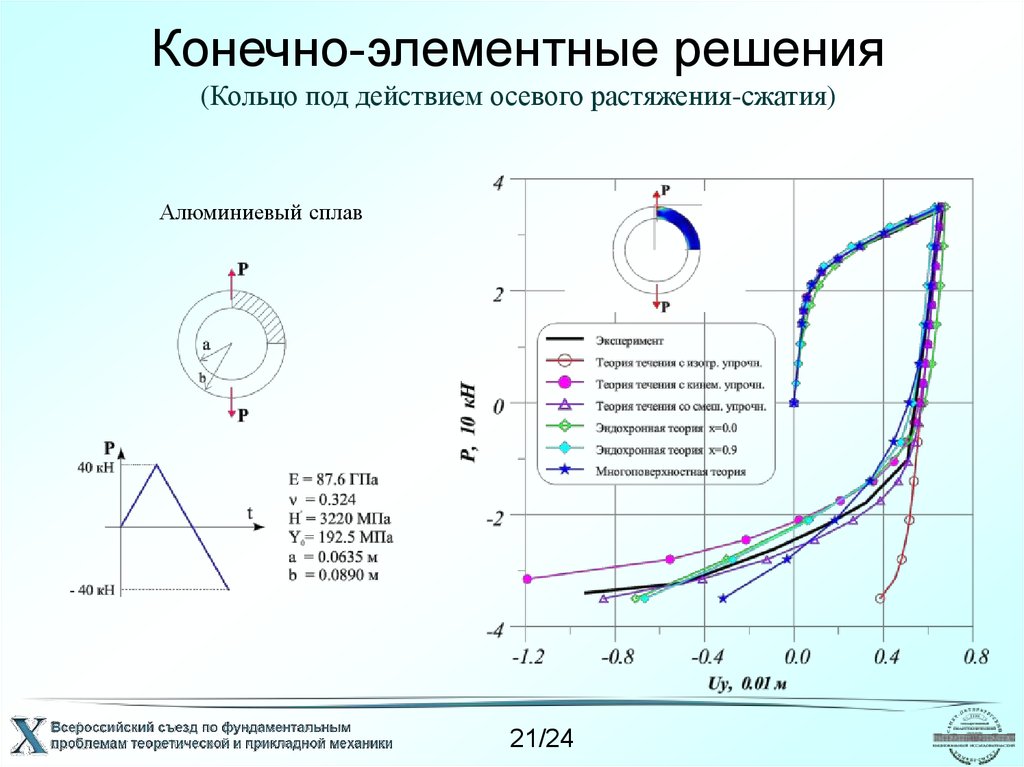
21. Конечно-элементные решения (Кольцо под действием осевого растяжения-сжатия)

Алюминиевый сплав
21/24

22. Конечно-элементные решения (Узел крепления под циклической нагрузкой)

Сталь 09Г2С
22/24

23. Заключение

• Экспериментально получены поверхности
равных пластических податливостей
• Разработаны определяющие соотношения
теории
• Получен термодинамически корректный
вариант соотношений теории
• Разработаны алгоритм и КЭ реализация
теории
• Проиллюстрирована рациональность
применения теории для однородного и
неоднородного напряженных состояний в
случае сложного пассивного нагружения
23/24

24. Благодарю за внимание!

24/24

25. Изменение скорости ползучести от времени

25/24