Дифракционная теория изображений

1. Дифракционная теория изображений

Будак Владимир Павлович,
Национальный исследовательский
университет «МЭИ»
кафедра светотехники
: +7 (095) 763-5239
[email protected]

2. Описание электромагнитного поля

Уравнения Maxwell (James Clerk, 1831–1879)
rot H
1 D 4
1 B
j, rot E
, div D 4 , div B 0, B H, D E
c t
c
c t
Волновое уравнение
1 2E
c
E 2 2 0, v , n
v t
n
1 2
(r, t ) 2 2 0 : (r, t ) U (r ) e i t d U (r) k 2U 0
v t
Дифракция - метод приближенного решения волнового уравнения:
• окончательные выражения - формулы Fresnel для поля за отверстием или за
препятствием
• в узком смысле - отклонение от законов геометрической оптики
• в более широком смысле – приближенное описание распространения
электромагнитной волны
Не всегда следует искать громоздкое точное аналитическое
решение, а затем упрощать его к виду удобному для анализа

3. Задача дифракции

(V)
(Σ)
ˆ
N
P
(Σ')
ε
R
U k 2U 0, U (r) r V (r)
U k 2U 0, U (r) r V (r)
3
(U
U
U
U
)d
r 0
U U U U 0
(V )
div(U U U U ) U U U U U U U U U U U U
Теорема Gauβ:
(U U U U )d r (U U U U )Nˆ d
3
2
r 0
( )
(V )
eikR
eikR
1 eikR ˆ
U (r)
: U
ik
R
R
R
R R
(U U U U )Nˆ d
( )
2
r
(U U U U )Nˆ d
( )
Решение волнового уравнения для точечного источника
известно точное
2
r

4. Интеграл Kirchhoff (Gustav Robert 1824-1887)

ikR
ikR
e
1
e
ˆd r
ˆ N
ˆ d 2r
I (U U U U )N
U
U
ik
R
R
R R
( )
( )
2
eik 2
ˆ U dN
ˆ eik
I 2 U (ik 1) N
0
U ( 1) dNˆ 4 U ( P)
0
ˆ
eikR ˆ 2
1
R
U ( P)
N d r
U (r )(ikR 1) U
4 ( )
R
R
σ
P
kR
ikR
1
e
ˆ V (r) V
ˆ d 2r
1: U ( P)
ik
R
N
R
4 ( )
ˆ V (r ) ikV (r )R
ˆ
eikz ik eikz R
ik
eikR ˆ ˆ 2
U ( z, )
V ( )
(R, N)d
2 ( )
R
На границе отверстия скачком изменяется от 0 до некоторого
значения, как амплитуда поля, так и ее производная поля

5. Дифракция Fresnel (Augustin-Jean 1788–1827)

Y
ik
eikR ˆ ˆ 2
U ( z, )
V ( )
(R, N)d
2 ( )
R
’ R
ˆ ,N
ˆ) z , 1 1
(R
R R2 z 2
( ) 2
( ) 2
R z ( ) z 1
z
2
z
2z
X
2
2
O
P
k eikz
U ( z , )
2 iz
k
Z
z3
( ) 2 2
( ) V ( ) exp ik 2 z d
4
2 z
3
- 1см при длине волны =1мкм
составит z>>0.3м
Более точные оценки z 400
Приближение Fresnel можно считать практически точным в
задачах прикладной оптики

6. Дифракция Fraunhofer (Joseph von, 1787-1826)

ikz
2
2z
ik
ke
( )2 2 2
U ( z , )
V ( )e z d 2
2 iz ( )
2z
2z
z
2
2
k
2 z
:
- 1см при длине волны =1мкм - z>>100м
2z
Дифракция Fraunhofer на круглом отверстии радиуса a:
a 2
a
2
U ( z, ) A exp ik
d A exp ik
cos d d 2 A J 0 k
d
z
z
z
( )
0 0
0
1.2
d z J1 ( z ) z J 0 ( z )dz U ( z, ) a 2 A
ka n 3.83 n 0.61
a
2J1 k a
k a
1
0.8
0.6
0.4
0.2
0
-0.2
- кружок рассеяния Airy
0
1
2
3
4
5
6
7
8
9
10

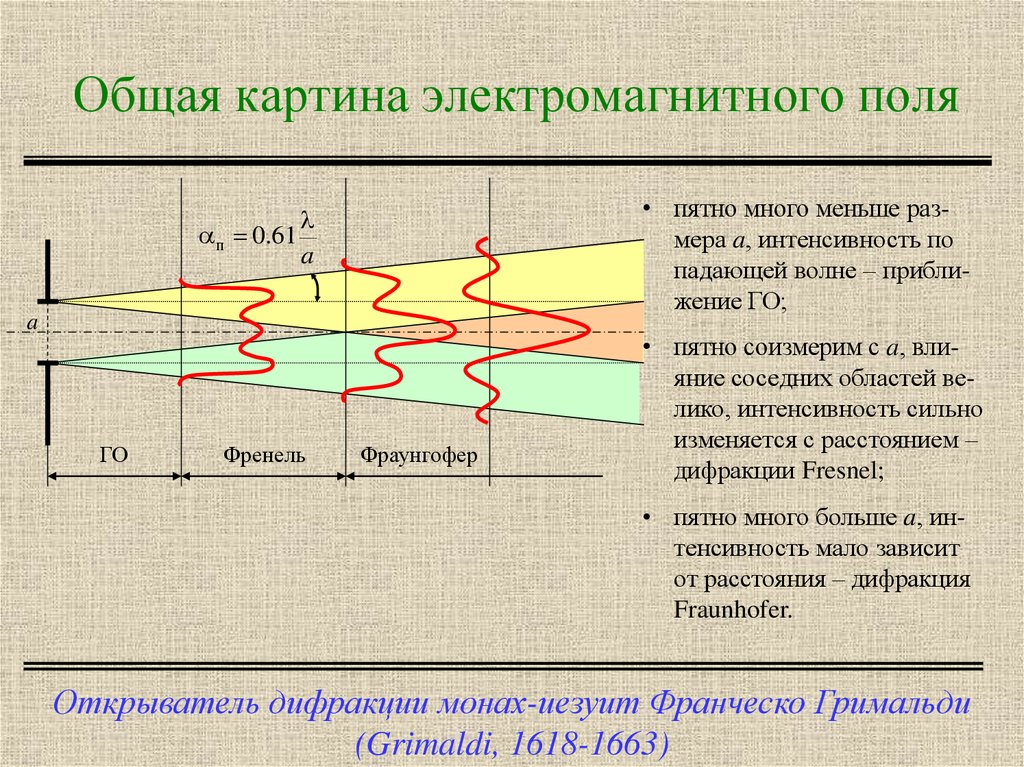
7. Общая картина электромагнитного поля

• пятно много меньше размера a, интенсивность по
падающей волне – приближение ГО;
п 0.61
a
a
ГО
Френель
Фраунгофер
• пятно соизмерим с a, влияние соседних областей велико, интенсивность сильно
изменяется с расстоянием –
дифракции Fresnel;
• пятно много больше a, интенсивность мало зависит
от расстояния – дифракция
Fraunhofer.
Открыватель дифракции монах-иезуит Франческо Гримальди
(Grimaldi, 1618-1663)

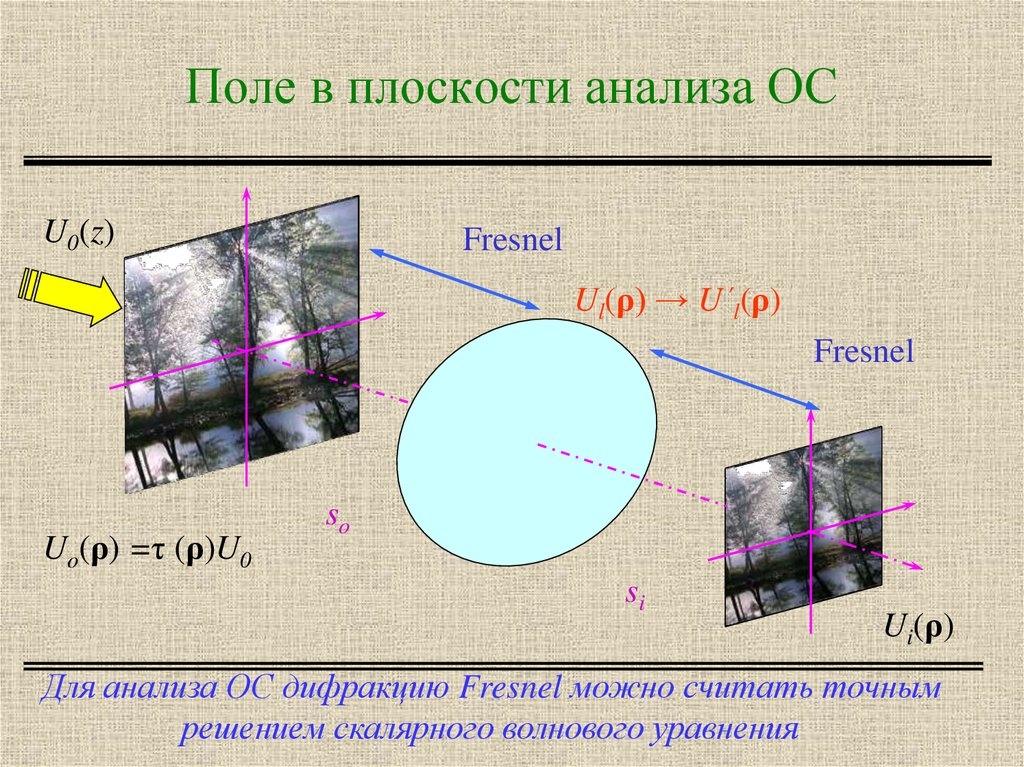
8. Поле в плоскости анализа ОС

U0(z)
Fresnel
Ul(ρ) → U´l(ρ)
Fresnel
Uo(ρ) =τ (ρ)U0
so
si
Ui(ρ)
Для анализа ОС дифракцию Fresnel можно считать точным
решением скалярного волнового уравнения

9. Действие тонкой линзы

Δ1
Δ2
U´l(ρ)=Ul(ρ)·τ (ρ),
τ (ρ)=Θ(ρ)·exp{ikφ(ρ)}
1, ;
(
)
Зрачковая функция:
0, .
Δ
R2
Оптический путь луча в линзе φ(ρ):
( ) n ( ) 0 ( ) 0 (n 1) ( )
Ul(ρ)
Δ01
Δ02
Δ0
ρ
U´l(ρ)
Δ´0
R
R
( ) 1 0 2 01 R1 R12 2
R1
R
02
2
R22
2
0
2
2
0 R1 1 1 R2 1 1
R1
R2
Приближение параксиальной оптики: ρ»R

10. Параксиальная оптика

Аналогично приближению дифракции Fresnel – разложение в ряд Taylor сохранением 2 членов:
1
R
Откуда:
2
1
1
2 R
2
2
( ) 0
2
1
1
R
R
2
1
1
2 1
1
2
1
( ) 0 ( n 1) 0
n
(
n
1)
0
2
R
R
2
R
R
2
2
1
1
Заднее фокусное расстояние тонкой линзы:
1
1
1
2
(n 1) ( ) n 0
f
2f
R1 R2
Действие тонкой линзы в параксиальном приближении сводится к множителю:
2
U l ( ) U l ( ) ( ) exp ikn 0 ik
2
f
Тонкая линза в параксиальном приближении изменяет амплитуду
падающей волны по зрачковой функции, а фазу - квадратично

11. Формирование изображения ОС

Поле на линзе – дифракция Fresnel:
( 1 )2 2
k eikso
Ul ( 1 )
Uo ( ) exp ik
d
2s
2 iso
Поле после тонкой линзы:
12
U l ( 1 ) U l ( 1 ) ( 1 ) exp ikn 0 ik
2
f
Поле на экране – дифракция Fresnel:
( 1 2 )2 2
k eiksi
Ui ( 2 )
U l ( 1 ) exp ik
d 1
2
s
2 isi
i
Собирая все члены вместе получим:
ik ( s s n )
k e o i 0
U i ( 2 )
si so
2
2
ik
U o ( ) ( 1 ) exp 2
( 1 ) 2 12 ( 1 2 ) 2 2 2
d d 1
s
f
s
i
Упрощение выражения возможно из анализа части
подынтегрального выражения в квадратных скобках

12. Комплексная амплитуда в изображении

2
( 1 ) 2 12 ( 1 2 ) 2 2
1 1 22
2 1
1 1
s
f
si
s
so f si si
s0 si
1 1
1
Плоскости объекта и изображения - сопряженные:
so si
f
Проведем замену переменных:
si2 2
s
2
1
2
2
o , i , 1 , d 2 d o , d 2 1 2 d 2 1 , i , k
si
so
si
so
что приведет к выражению для поля комплексной амплитуды в изображении
A
Ui ( i ) Uo ( o ) ( 1 ) exp i o2 i 2 1 i o d 2 o d 2 1
Допустим, что система является узкопольной и ρо→0. Тогда
U i ( i )
A
2
2
2
U
(
)
(
)
exp
i
2
d
d
U
(
)
F
(
)
d
o
o
o
1
1
i
o
1
o
o
o
i
o
- т.е. интегралу свертки: тонкая линза в параксиальном
приближении является линейной системой

13. Произвольная оптическая система

В случае оптической системы из многих компонент:
1.
Учет аберраций и конечной толщины изменит выражение для оптического пути в
линзе φ(ρ1)
2.
Многолинзовость изменит соотношение сопряжения объекта и изображения
Ui ( i ) Uo ( o ) P( o i )d 2 o
причем в общем случае
P( o i )
A
( 1 ) exp i 2 1 i o iW ( 1 , o ) d 2 1
Произвольная ОС линейна относительно комплексной амплитуды