Похожие презентации:
Структуры и алгоритмы обработки данных
1. Структуры и алгоритмы обработки данных
• Данные;• Структура данных;
• Данные статической структуры;
• Данные динамической структуры;
• Типы данных линейной структуры;
• Типы данных нелинейной структуры.
2.
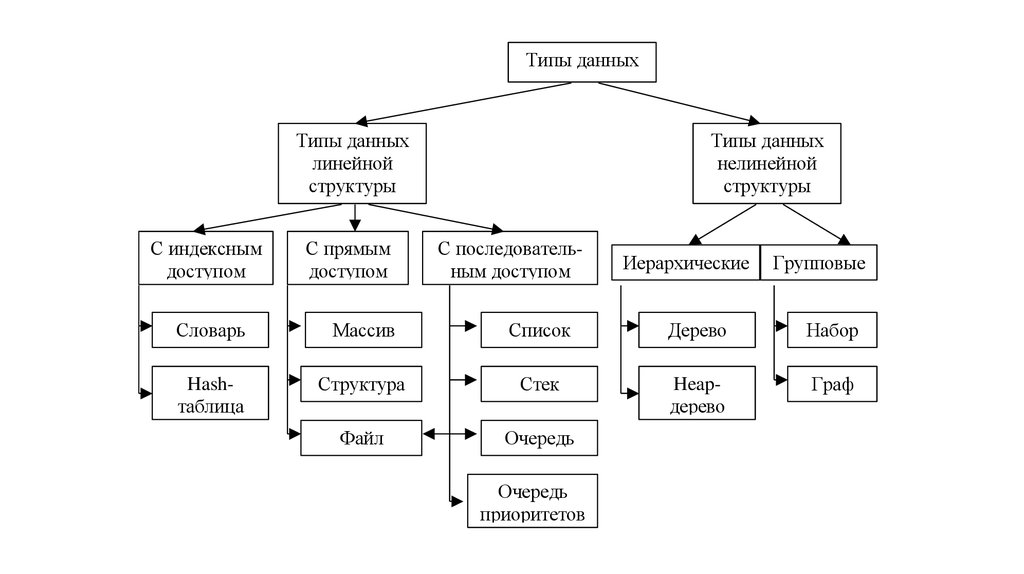
Типы данныхТипы данных
линейной
структуры
С индексным
доступом
С прямым
доступом
Типы данных
нелинейной
структуры
С последовательным доступом
Иерархические
Групповые
Словарь
Массив
Список
Дерево
Набор
Hashтаблица
Структура
Стек
Heapдерево
Граф
Файл
Очередь
Очередь
приоритетов
3. Анализ алгоритмов
Факторы, влияющие на время выполненияпрограммы:
- Ввод исходной информации;
- Качество скомпилированного кода;
- Машинные инструкции, используемые для
выполнения программы;
- Временная сложность алгоритма.
T(n)
c, n0
O(n2)
n>=n0, T(n)<=cn2
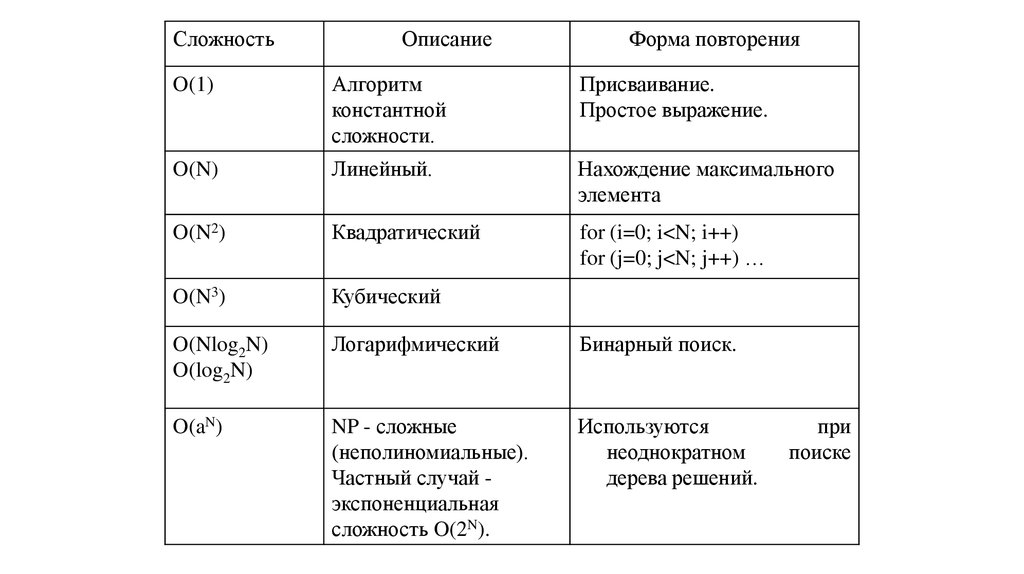
4.
СложностьОписание
Форма повторения
O(1)
Алгоритм
константной
сложности.
Присваивание.
Простое выражение.
O(N)
Линейный.
Нахождение максимального
элемента
O(N2)
Квадратический
for (i=0; i<N; i++)
for (j=0; j<N; j++) …
O(N3)
Кубический
O(Nlog2N)
O(log2N)
Логарифмический
Бинарный поиск.
O(aN)
NP - сложные
(неполиномиальные).
Частный случай экспоненциальная
сложность O(2N).
Используются
неоднократном
дерева решений.
при
поиске
5.
Функции времени выполнения для программ с различнойвременной сложностью
3500
2n
3000
n3/2
2000
100n
1500
1000
500
n
29
27
25
23
21
19
17
15
13
11
9
7
5
3
0
1
T(n)
2500
5n2
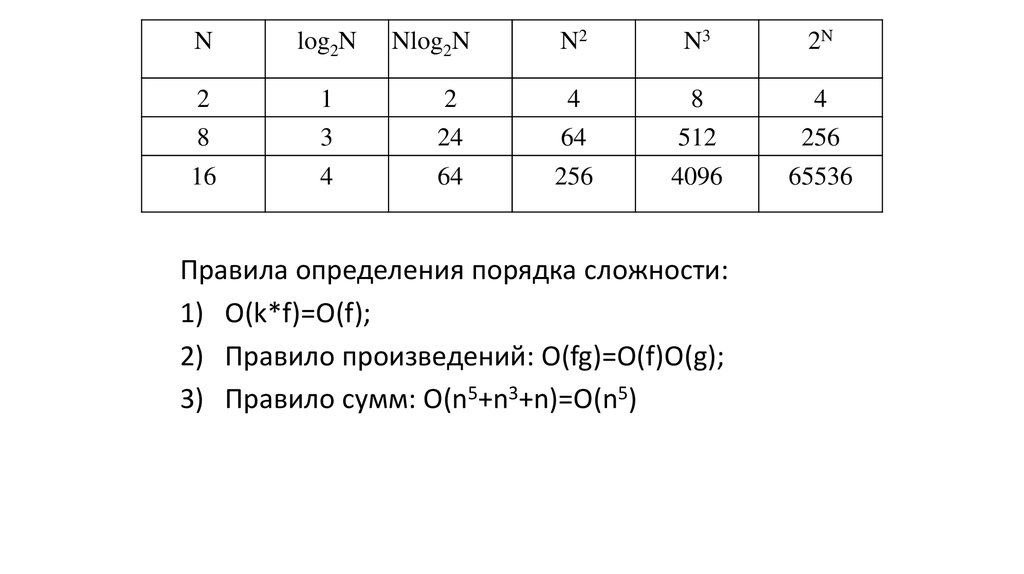
6.
N2N3
2N
2
4
8
4
3
24
64
512
256
4
64
256
4096
65536
N
log2N
2
1
8
16
Nlog2N
Правила определения порядка сложности:
1) O(k*f)=O(f);
2) Правило произведений: O(fg)=O(f)O(g);
3) Правило сумм: O(n5+n3+n)=O(n5)
7.
(1) for (int i=0; i<n-1; i++)(2) for (int j=n-1; j>i; j--)
(3)
if (a[j-1]>a[j]) {
(4)
temp=a[j-1];
(5)
(6)
a[j-1]=a[j];
a[j]=temp;
}
n 1
(n i) n(n 1) / 2 n
i 1
O(n2)
O(n-i)
O(1)
2
/2 n/2
8.
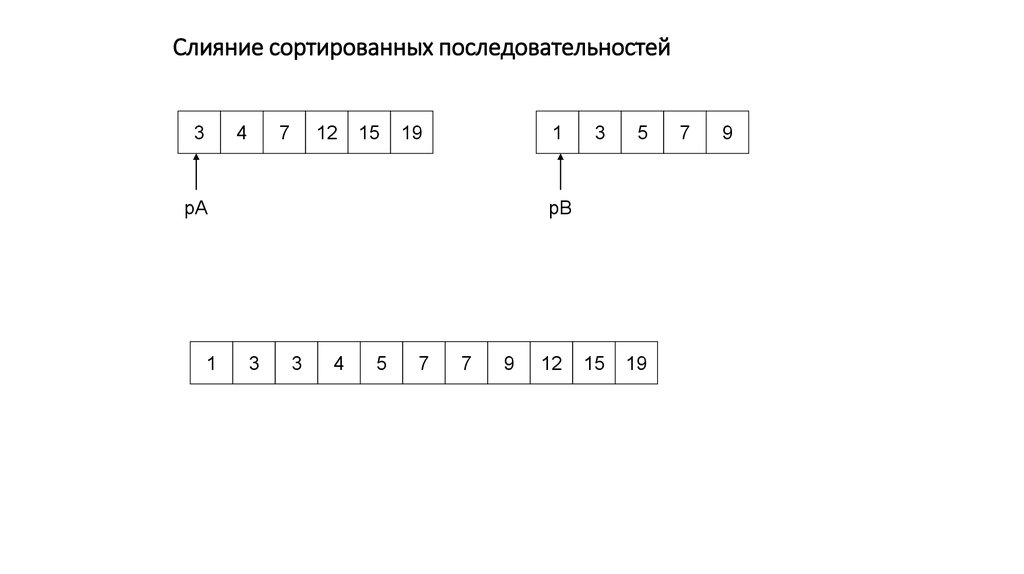
Слияние сортированных последовательностей3
4
7
12
15
19
1
pA
1
3
5
15
19
pB
3
3
4
5
7
7
9
12
7
9
9. Анализ рекурсивных программ
Последовательный поискint search(int a[ ],int n,int key)
{
for (int i=0;i<n;i++)
if (a[i]==key) return i;
return -1;
}
10. Слияние сортированных последовательностей
Бинарный поискА(n), low=0, high=n-1.
Алгоритм бинарного поиска:
• mid=(low+high)/2.
• А[mid]==key
• A[mid]<key
• A[mid]>key
11. Последовательный поиск
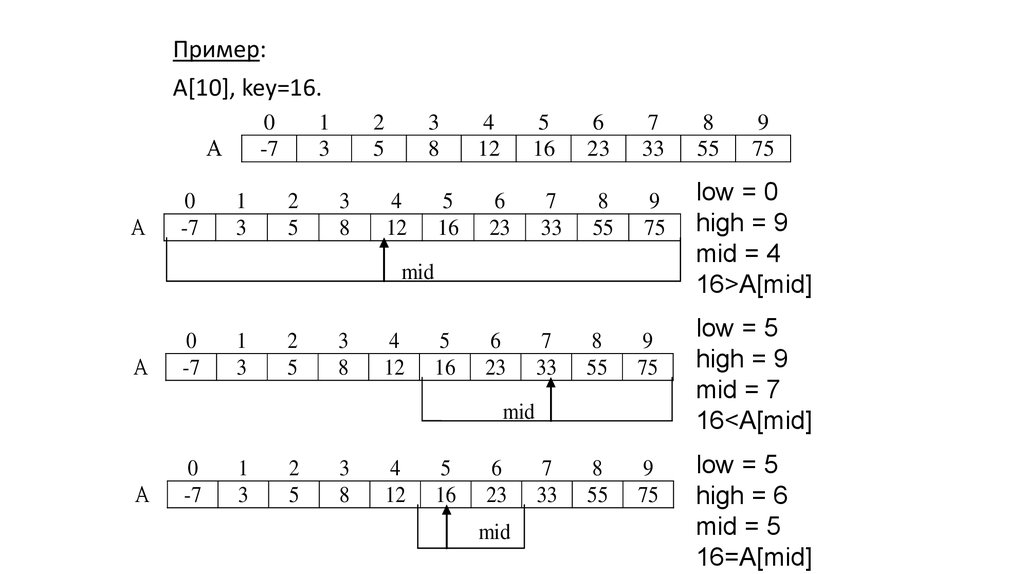
Пример:А[10], key=16.
0
-7
А
А
0
-7
1
3
1
3
2
5
2
5
3
8
3
8
4
12
4
12
5
16
6
23
7
33
8
55
low = 0
high = 9
mid = 4
16>A[mid]
5
16
6
23
7
33
8
55
9
75
5
16
6
23
7
33
8
55
9
75
7
33
8
55
9
75
mid
А
0
-7
1
3
2
5
3
8
4
12
mid
А
0
-7
1
3
2
5
3
8
4
12
5
16
6
23
mid
9
75
low = 5
high = 9
mid = 7
16<A[mid]
low = 5
high = 6
mid = 5
16=A[mid]
12. Бинарный поиск
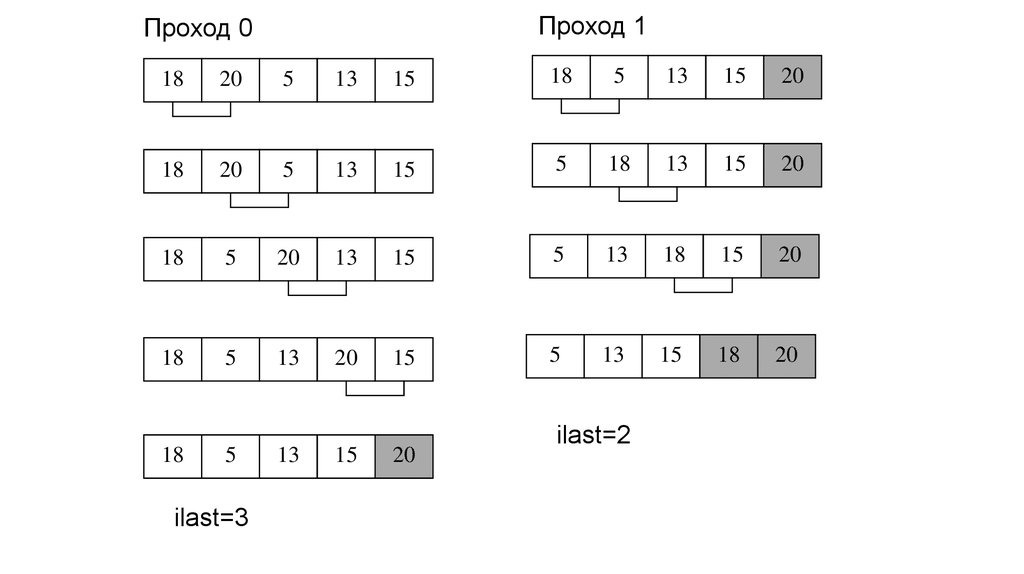
Алгоритмы сортировки массивовСортировка посредством выбора
Пример.
Массив содержит целые числа 18, 20, 5, 13, 15.
18
20
5
13
15
18
13
15
проход 0
5
20
5
13
15
20
проход 1
5
13
18
18
проход 3
20
проход 2
15
5
13
15
18
O(n2)
20
13.
Сортировка обменом (пузырек)начальный
массив
44
55
12
42
94
18
06
67
i=2
06
44
55
12
42
94
18
67
i=3
06
12
44
55
18
42
94
67
i=4
06
12
18
44
55
42
67
94
i=5
06
12
18
42
44
55
67
94
i=6
06
12
18
42
44
55
67
94
i=7
06
12
18
42
44
55
67
94
i=8
06
12
18
42
44
55
67
94
14. Алгоритмы сортировки массивов
Проход 1Проход 0
18
20
5
13
15
18
5
13
15
20
18
20
5
13
15
5
18
13
15
20
18
5
20
13
15
5
13
18
15
20
18
5
13
20
15
5
13
15
18
20
18
5
ilast=3
13
15
20
ilast=2
15.
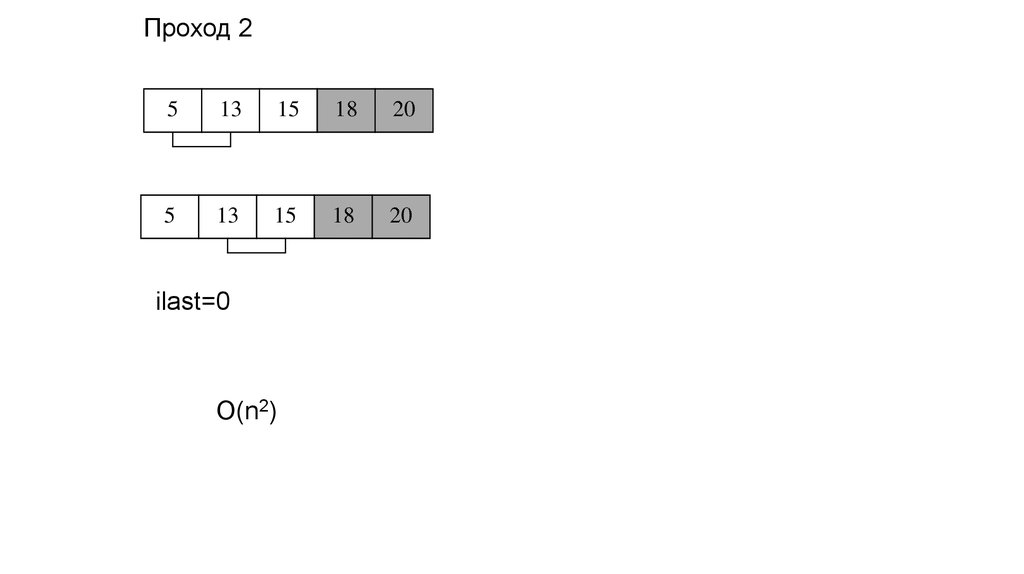
Проход 25
13
15
18
20
5
13
15
18
20
ilast=0
O(n2)
16.
Шейкер-сортировканачальный
массив
ll=1
kk=7
44
55
12
42
94
18
06
67
2
7
06
44
55
12
42
94
18
67
2
6
06
44
12
42
55
18
67
94
3
6
06
12
44
18
42
55
67
94
3
3
06
12
18
42
44
55
67
94
O(n2)
17.
Сортировка вставкамиА = 18, 20, 5, 13, 15
18
20
5
5
18
20
5
18
20
5
13
18
13
15
13
15
13
15
20
15
O(n2)
5
13
15
18
20
18. Шейкер-сортировка
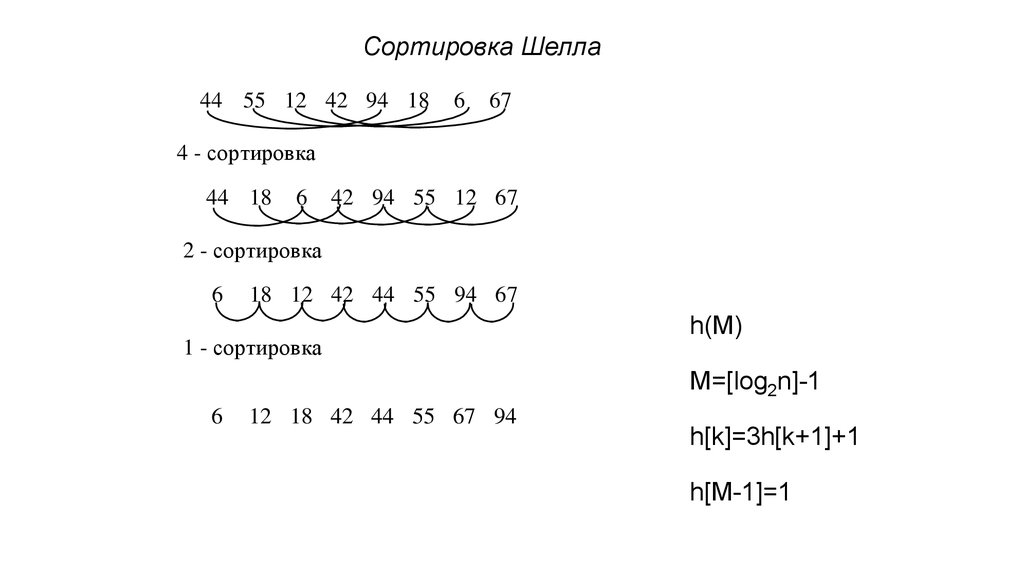
Сортировка Шелла44 55 12 42 94 18
6
67
4 - сортировка
44 18
6
42 94 55 12 67
2 - сортировка
6
18 12 42 44 55 94 67
1 - сортировка
h(M)
M=[log2n]-1
6
12 18 42 44 55 67 94
h[k]=3h[k+1]+1
h[M-1]=1
19. Сортировка вставками
Сортировка с разделением (быстрая)O(n log2n)
20.
Сравнение алгоритмов сортировки1.
Сортировка Шелла
2.
3.
4.
Сортировка простыми вставками
Сортировка бинарными вставками
Сортировка простым выбором
5.
6.
Шейкер-сортировка
Сортировка пузырьком












 Информатика
Информатика








