Методы сортировки

1. Структуры и алгоритмы обработки данных

Восточно-Сибирский государственный технологический
университет
Кафедра «Системы информатики»
Структуры и алгоритмы
обработки данных
Лекция по теме:
Методы сортировки
Бильгаева
Людмила Пурбоевна
Улан-Удэ, 2014

2. Основные определения

Сортировка - это процесс упорядочения
некоторого множества элементов, на
котором определены отношения порядка
>, <, , .
Различают упорядочение множества
элементов по возрастанию или
убыванию.

3.

Сложность алгоритма - одночлен,
отражающий порядок величины требуемого
ресурса (времени/дополнительной памяти) в
зависимости от размерности задачи.
Временная (пространственная) сложность не
позволяет определить время (необходимый
объем дополнительной памяти) работы
алгоритма, но она позволяет оценить динамику
роста времени (объема дополнительной
памяти), необходимого для работы метода, при
увеличении размерности задачи.

4.

Например, для алгоритма с временной
сложностью T(n2) при достаточно больших
n можно утверждать, что при увеличении
размера задачи (при сортировке - размера
массива) в 3 раза время работы алгоритма
увеличится в 32=9 раз.
Если операция выполняется за
фиксированное число шагов, не зависящее
от размера задачи, то принято писать T(1).

5.

Методы сортировки
Внутренняя
Внешняя
1. Данные находятся в ОЗУ
2. Необходимо
оптимизировать
число действий программы
(число сравнений,
обменов элементов)
1. Данные хранятся на ВЗУ
с медленным доступом (диск).
2. Необходимо уменьшить число
обращений к этому
устройству.

6. Классификация методов внутренней сортировки

Сортировка
Включением
Извлечением
Простым
включением
Методом
Шелла
Подсчетом
Распределением
Слиянием
Простым
извлечением
Древесным
Обменом
Простым
обменом
Методом
Хоара
Просмотр методов можно выполнить по гиперссылке

7. Простое включение

Дана числовая последовательность: 10, 5, 80, 6, 35.
Выполнить сортировку включением.
Для сортировки требуется дополнительная память для
размещения отсортированной последовательности.
A1, A2, A3, A4, A5 - исходная последовательность
B1, B2, B3, B4, B5 - отсортированная последовательность
Исходная
память
Дополнительная
память
A1 A2 A3 A4 A5
B1 B2 B3 B4 B5
10
5
80
6
35

8. Сортировка подсчетом

Дана числовая последовательность: 10, 5, 80, 6, 35.
Выполнить сортировку подсчетом.
Суть метода заключается в нахождении местоположения
элемента в последовательности, т.е. его номер К+1
К
0
1
2
3
4
+
+
+
+
+
+
+
+
+
Сколько раз каждый
элемент больше других
+
5
6
10
35
80

9. Простое извлечение

Дана числовая последовательность: 10, 5, 80, 6, 35.
Выполнить сортировку извлечением.
A1 A 2 A3 A4 A5
A1 A2 A3 A4 A5
A1 A2 A3 A4 A5
10
5
5
5
80
6
35
Определить минимальный
элемент
10 80
6
35
80 10 35
Определить минимальный
элемент
Определить минимальный
элемент
5
6
10
6
A1 A2 A3 A 4 A5
A1 A2 A 3 A4 A5
5
5
6
10 80 35
Определить минимальный
элемент
35
6
10 35 80
Отсортированная
последовательность

10. Древесная сортировка

Сортировка называется древесной, потому что в этом методе
используется структура данных, называемая двоичным деревом (рис 1).
При древесной сортировке нет необходимости каждый раз находить
максимальный элемент. В методе поддерживается такой порядок, при
котором максимальный элемент всегда будет оказываться в вершине
дерева
(1)
(2)
(3)
(4)
(8)
(5)
(9)
(10)
(6)
(11)
(12)
(7)
(13)
(14)
Рисунок 1. Структура двоичного дерева
(15)

11.

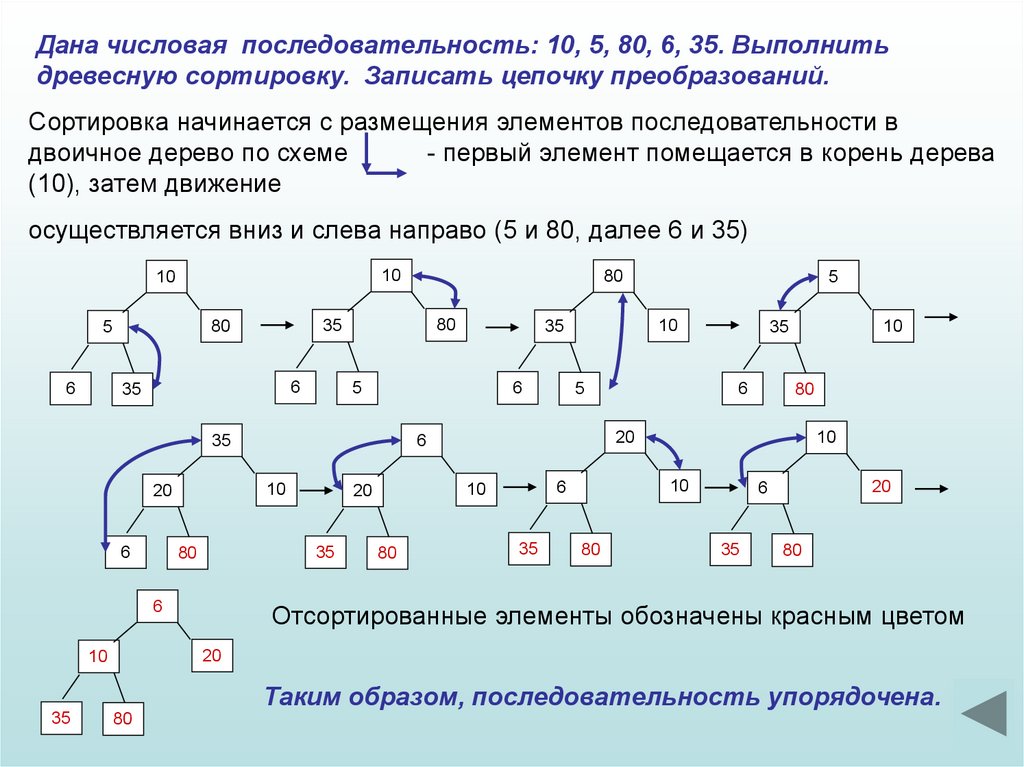
Дана числовая последовательность: 10, 5, 80, 6, 35. Выполнить
древесную сортировку. Записать цепочку преобразований.
Сортировка начинается с размещения элементов последовательности в
двоичное дерево по схеме
- первый элемент помещается в корень дерева
(10), затем движение
осуществляется вниз и слева направо (5 и 80, далее 6 и 35)
10
10
6
80
35
80
5
6
35
6
6
35
80
6
80
80
20
35
10
10
6
10
20
10
35
6
5
6
10
5
10
35
5
35
20
80
80
20
6
35
80
Отсортированные элементы обозначены красным цветом
20
10
Таким образом, последовательность упорядочена.
35
80

12. Простой обмен

Дана числовая последовательность: 10, 5, 80, 6, 35.
Выполнить сортировку методом пузырька.
При простом обмене максимальный элемент последовательности за
первый проход достигает своего места, т.е. подобно пузырьку «всплывает
на поверхность».
10 5 80 6 35
- Исходная последовательность
В данном примере после первого прохода элемент «80» переместится на
свое место
10 5 80 6
35
После второго прохода получим
отсортированную последовательность
5 10 6 35 80

13. Метод Хоара

Дана числовая последовательность: 10, 5, 80, 6, 35, 4, 15,1.
Выполнить сортировку методом Хоара.
i =j
Просмотр элементов
начинается с концов
последовательности до
тех пор, пока i не станет
равнымj
10
5
80
6
35
4
15
1
j
i
1
5
80
6
35
4
15 10
1
5
4
6
35 80 15 10
Последовательность отсортирована относительно центра
Двойными
стрелками
показаны обмены
Отсортированная
последовательность
1
5
4
1
5
4
6
35 80 15 10
i
j
10 80 15 35
1
4
5
6
10 15 80 35
1
4
5
6
10 15 35 80
i
6
j

14. Сортировка слиянием

Дана числовая последовательность: 10, 5, 80, 6, 35, 4, 15.
Выполнить сортировку слиянием.
10 5 80 6 35 4 15
Исходную последовательность
необходимо разбить на группы по
два элемента.
Внутри каждой группы элементы
упорядочить, используя любой
метод сортировки и т.д.
Выполнить сортировку обменом
5 10 6 80 4 35 15
Объединить группы и выполнить сортировку
5
6 10 80 4 15 35
Объединить группы и выполнить сортировку
Отсортированная последовательность
4
5
6 10 15 35 80

15. Сортировка распределением

Дана числовая последовательность: 3, 10, 8, 6, 5.
Выполнить сортировку вырожденным распределением.
Создать цикл, максимальный параметр которого равен
максимальному значению исходной последовательности. Затем
каждый элемент исходной последовательности сравнивается с
параметром цикла. Если элемент последовательности равен
параметру цикла, то он записывается в результирующую
последовательность.
1
0
2
0
3 4 5 6 7 8 9 10
1 0 1 1 0 1 0 1
A1
A2 A3
A4
A5

16. Теоретическая сложность методов сортировки

Методы
сортировки
Tmax
Tmid
Подсчетом
n2
Включением
Шелла
Tmin
n
n2
n2
Omax
n1,25
n
1
n
1
Извлечением
n2
1
Древесная
n*log(n)
1
Пузырьковая
Быстрая
Слиянием
Распределением
n2
n
n2
n*log(n)
1
log(n)
n*log(n)
n
n
n

17. Благодарю за внимание!

Желаю успехов в изучении методов
сортировки
Бильгаева Людмила Пурбоевна
к.т.н., доцент
кафедра «Системы информатики»
Восточно-Сибирский
государственный технологический
университет
E-mail: [email protected]
Благодарю за внимание!