Похожие презентации:
Работа с одной выборкой. Парные сравнения
1. Statistica Работа с одной выборкой Парные сравнения
2. Анализ единственной выборки
1.2.
3.
4.
5.
Определение шкалы измерения.
Проверка «нормальности» распределения для количественных
данных / определение типа распределения.
Попытки преобразования «ненормально» распределенных
переменных / анализ и поиск источников гетерогенности в
многомодальных распределениях.
Проверка предположения об отличии значения в выборки от какойлибо константы.
Подгонка, т.е. определение типа распределения.
3.
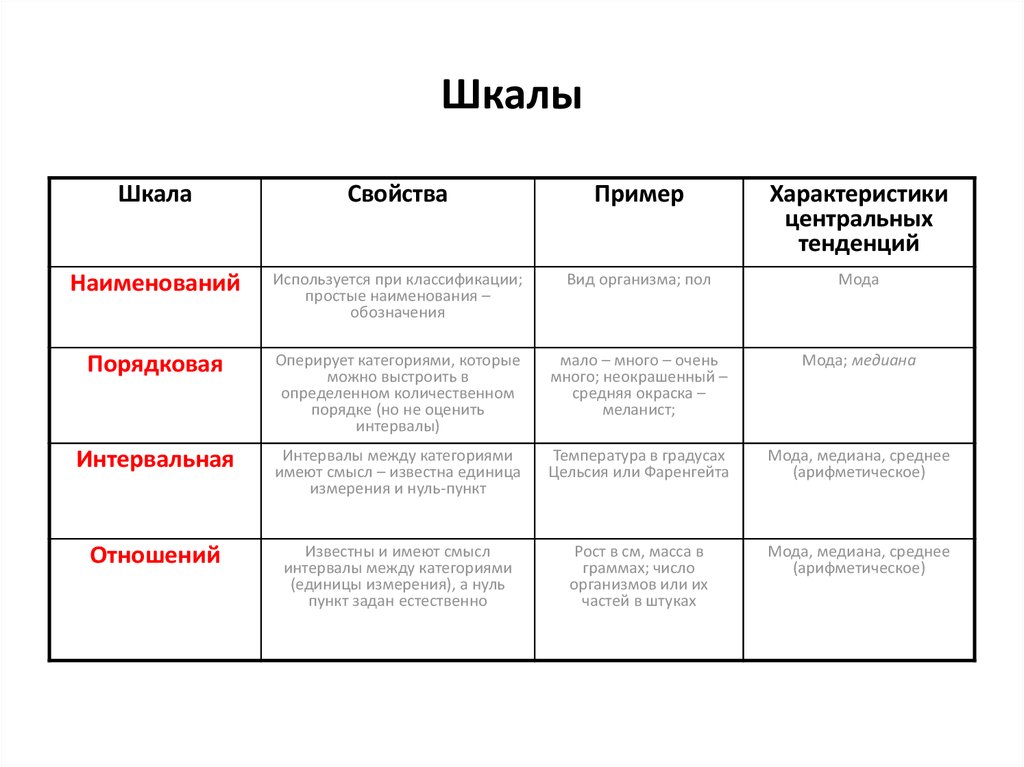
Актуальные области интересов:4. Шкалы
ШкалаСвойства
Пример
Характеристики
центральных
тенденций
Наименований
Используется при классификации;
простые наименования –
обозначения
Вид организма; пол
Мода
Порядковая
Оперирует категориями, которые
можно выстроить в
определенном количественном
порядке (но не оценить
интервалы)
мало – много – очень
много; неокрашенный –
средняя окраска –
меланист;
Мода; медиана
Интервальная
Интервалы между категориями
имеют смысл – известна единица
измерения и нуль-пункт
Температура в градусах
Цельсия или Фаренгейта
Мода, медиана, среднее
(арифметическое)
Отношений
Известны и имеют смысл
интервалы между категориями
(единицы измерения), а нуль
пункт задан естественно
Рост в см, масса в
граммах; число
организмов или их
частей в штуках
Мода, медиана, среднее
(арифметическое)
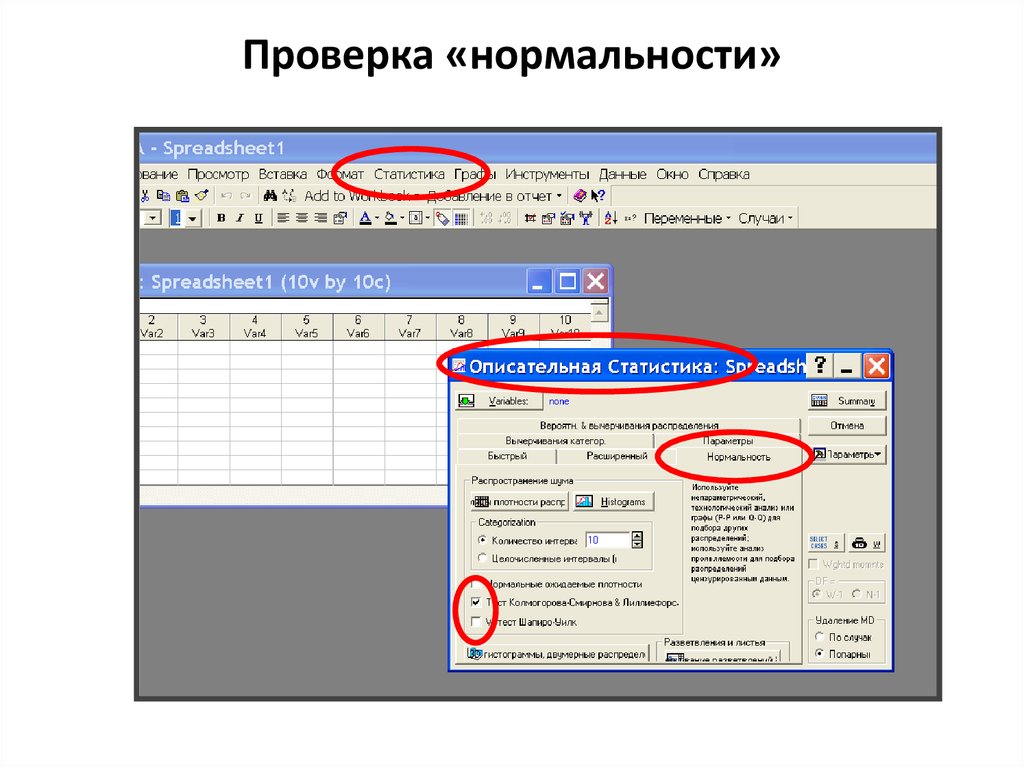
5. Проверка «нормальности»
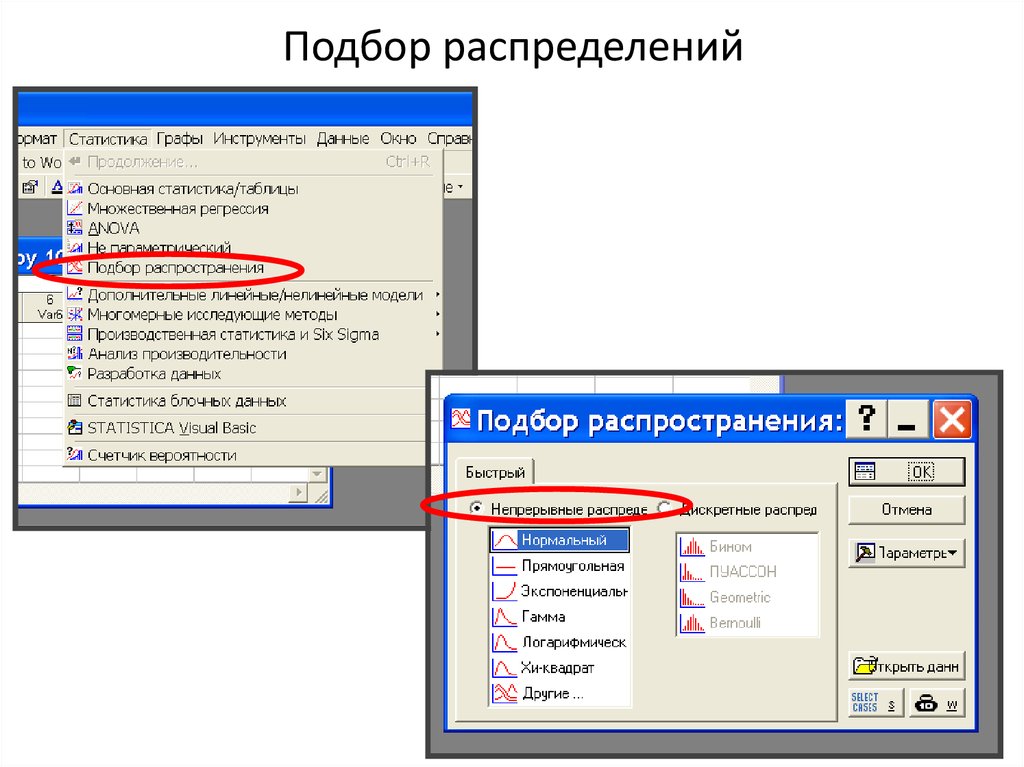
6. Подбор распределений
7. Трансформации переменных
Попробуем логарифмировать значения переменных«Cu_кисл», «Cd_кисл», «Pb_кисл», «Zn_кисл» в файле
«Пример_тм_токсичность_проверка.xls», находясь в
«STATISTICA».
Формула натурального логарифма в «STATISTICA»:
=log(x)
8. Трансформации переменных
9.
Что можно сравнивать?• Центральную тенденцию – среднее, медиану.
• Дисперсию, т.е. характер изменчивости.
• Тип распределения – тип изменчивости данных.
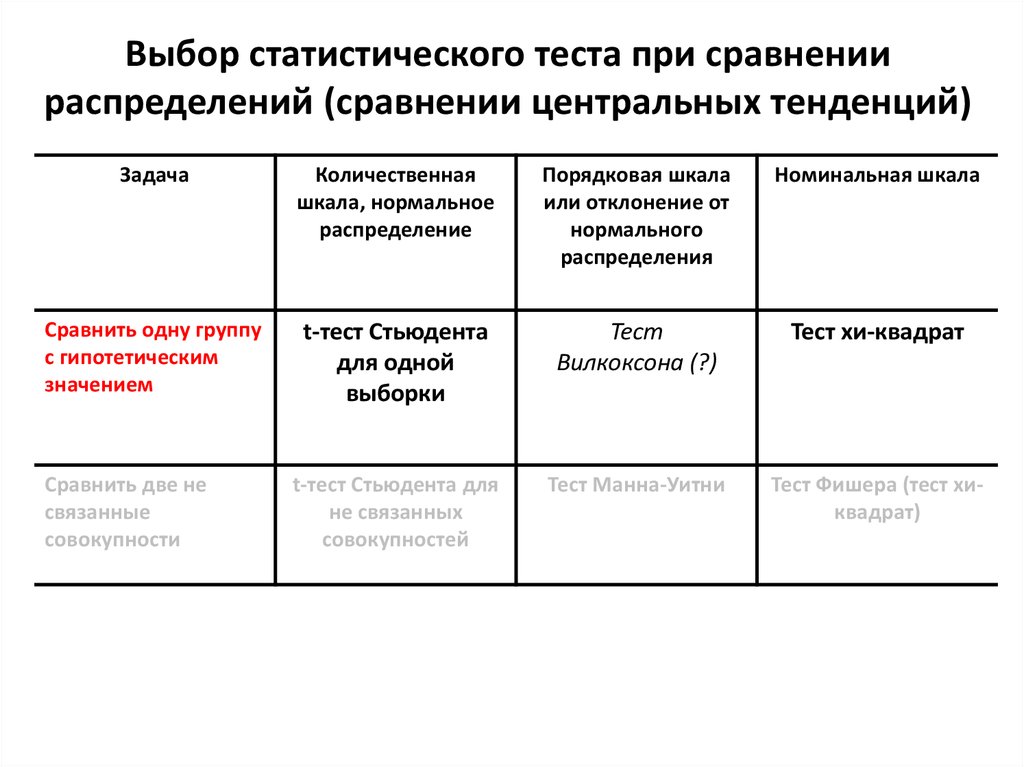
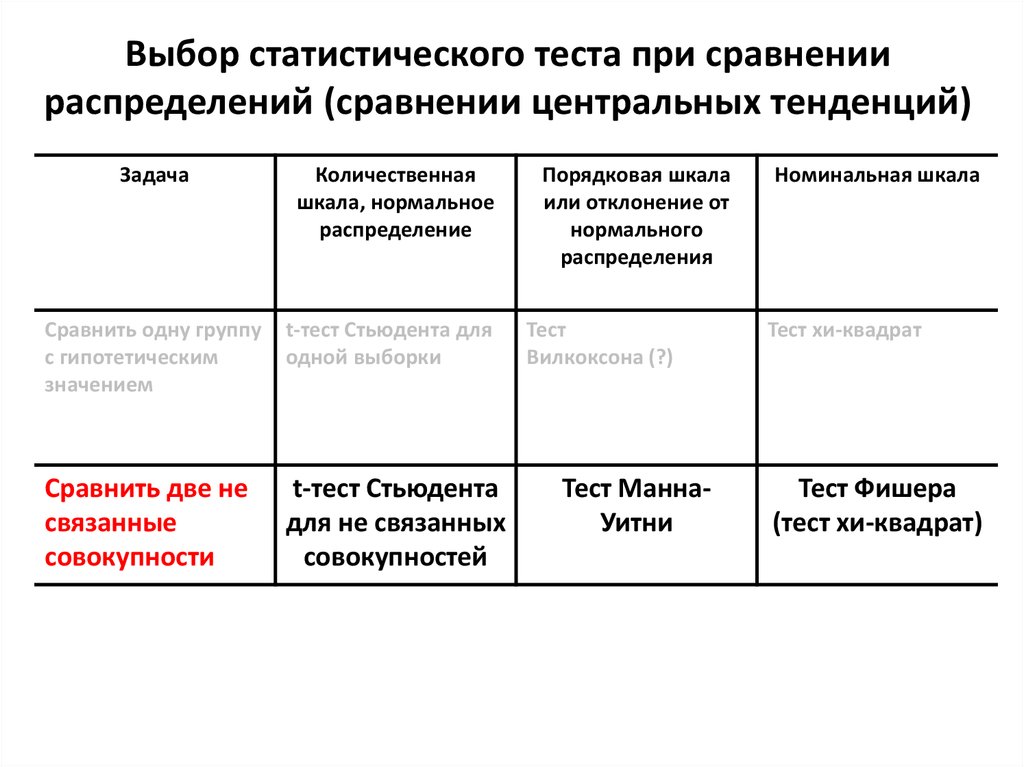
10. Выбор статистического теста при сравнении распределений (сравнении центральных тенденций)
ЗадачаКоличественная
шкала, нормальное
распределение
Порядковая шкала
или отклонение от
нормального
распределения
Номинальная шкала
Сравнить одну группу
с гипотетическим
значением
t-тест Стьюдента
для одной
выборки
Тест
Вилкоксона (?)
Тест хи-квадрат
t-тест Стьюдента для
не связанных
совокупностей
Тест Манна-Уитни
Тест Фишера (тест хиквадрат)
Сравнить две не
связанные
совокупности
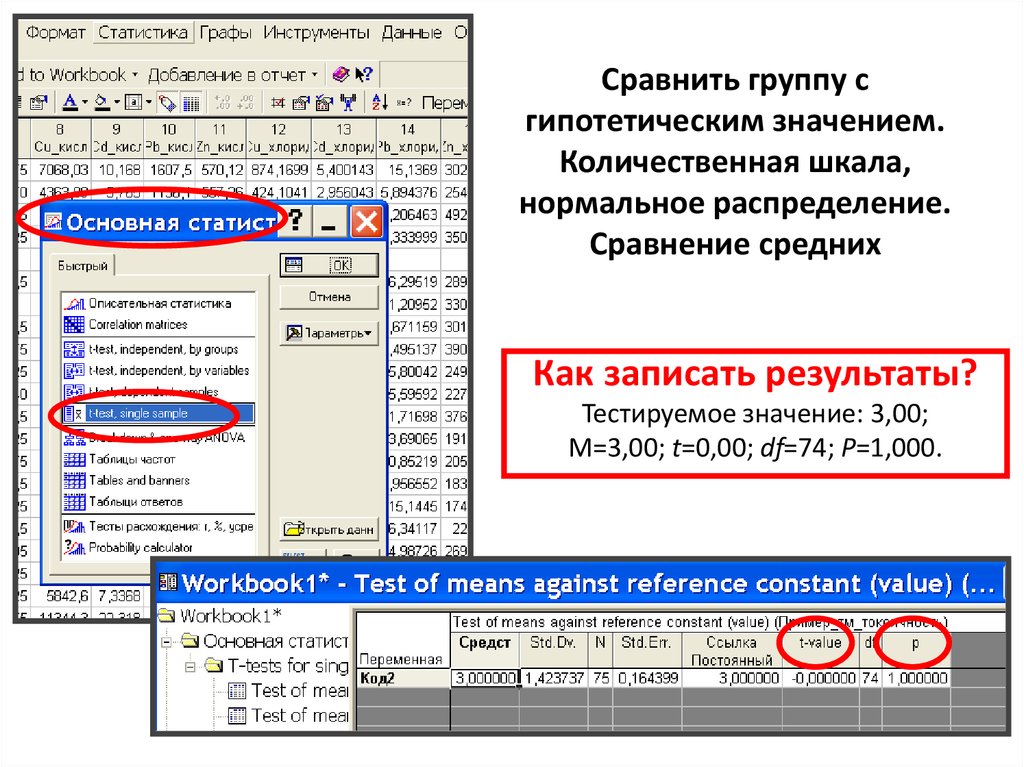
11. Сравнить группу с гипотетическим значением. Количественная шкала, нормальное распределение. Сравнение средних
Как записать результаты?Тестируемое значение: 3,00;
M=3,00; t=0,00; df=74; P=1,000.
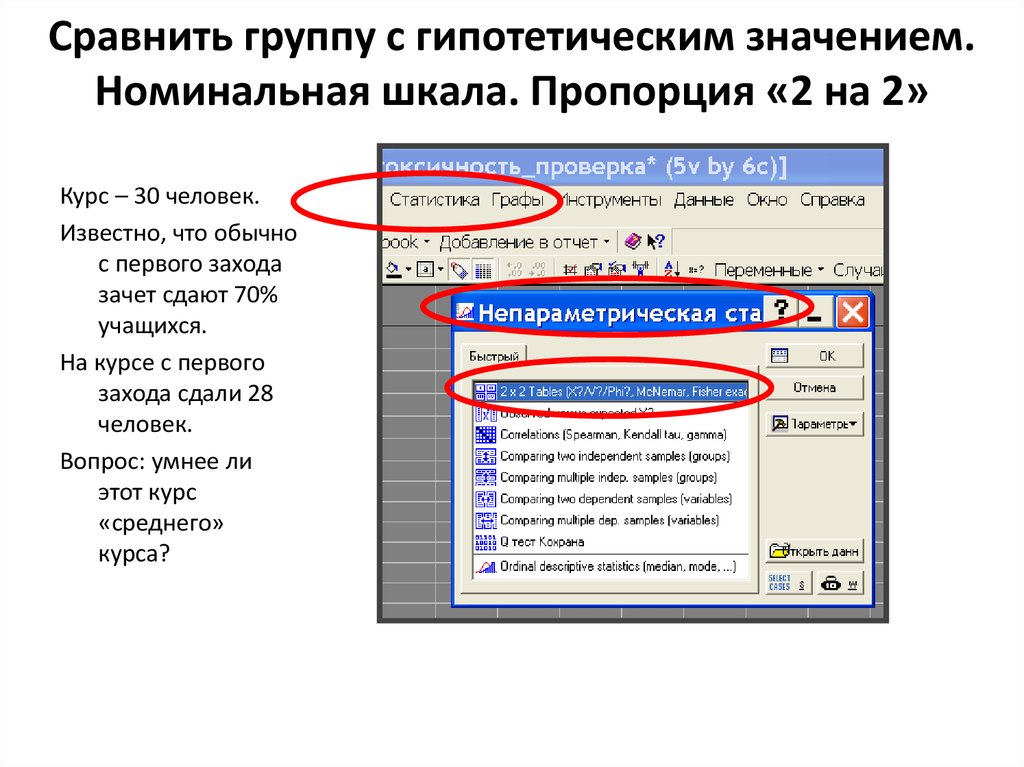
12. Сравнить группу с гипотетическим значением. Номинальная шкала. Пропорция «2 на 2»
Курс – 30 человек.Известно, что обычно
с первого захода
зачет сдают 70%
учащихся.
На курсе с первого
захода сдали 28
человек.
Вопрос: умнее ли
этот курс
«среднего»
курса?
13. Сравнить группу с гипотетическим значением. Номинальная шкала. Пропорция «2 на 2».
Курс – 30 человек.Известно, что обычно
с первого захода
зачет сдают 70%
учащихся.
На курсе с первого
захода сдали 28
человек.
Вопрос: умнее ли
этот курс
«среднего»
курса?
14. Сравнить группу с гипотетическим значением. Номинальная шкала.
Работаем с листом «Распределения»файла
«Пример_тм_токсичность_проверка.xls»
15. Выбор статистического теста при сравнении распределений (сравнении центральных тенденций)
ЗадачаКоличественная
шкала, нормальное
распределение
Сравнить одну группу
с гипотетическим
значением
t-тест Стьюдента для
одной выборки
Сравнить две не
связанные
совокупности
t-тест Стьюдента
для не связанных
совокупностей
Порядковая шкала
или отклонение от
нормального
распределения
Тест
Вилкоксона (?)
Тест МаннаУитни
Номинальная шкала
Тест хи-квадрат
Тест Фишера
(тест хи-квадрат)
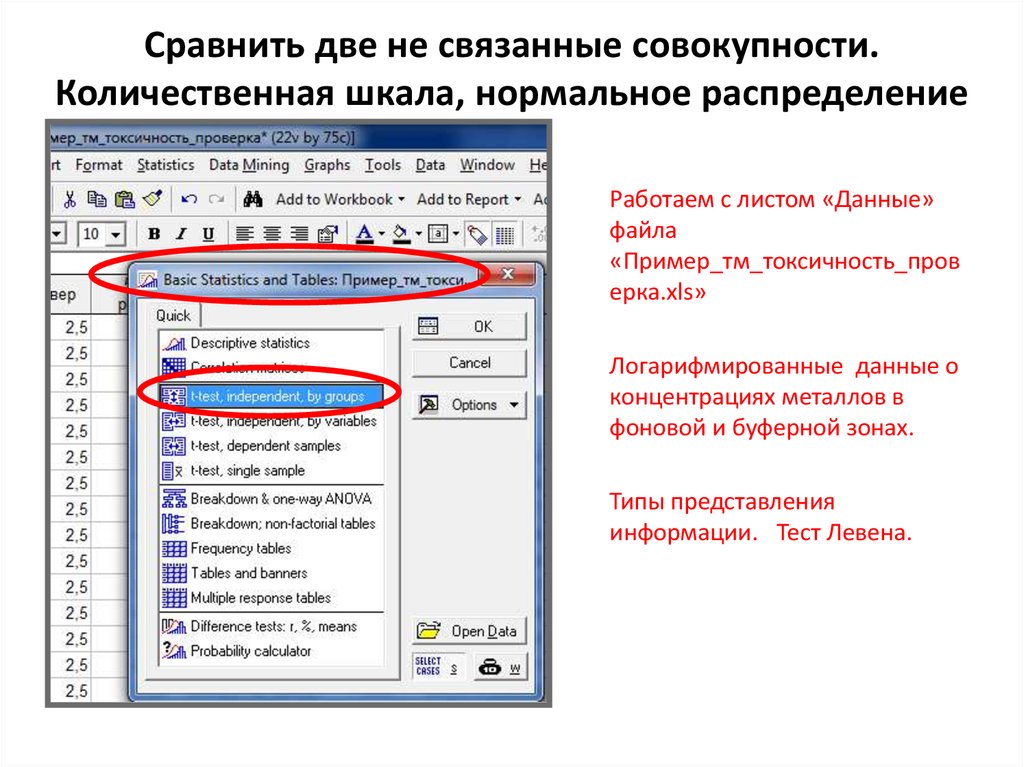
16. Сравнить две не связанные совокупности. Количественная шкала, нормальное распределение
Работаем с листом «Данные»файла
«Пример_тм_токсичность_пров
ерка.xls»
Логарифмированные данные о
концентрациях металлов в
фоновой и буферной зонах.
Типы представления
информации. Тест Левена.
17. Сравнить две не связанные совокупности. Количественная шкала, нормальное распределение. Как записать результаты?
Categ. Histogram: Cu_кисл_логЗона: 1 Cu_кисл_лог = 24*0,5*normal(x; 8,6815; 0,265)
Зона: 3 Cu_кисл_лог = 25*0,5*normal(x; 4,682; 0,3256)
Exclude condition: Зона=2
18
16
14
12
No of obs
10
8
6
4
2
0
3,0 4,0 5,0 6,0 7,0 8,0 9,0 10,0
3,5 4,5 5,5 6,5 7,5 8,5 9,5
3,0 4,0 5,0 6,0 7,0 8,0 9,0 10,0
3,5 4,5 5,5 6,5 7,5 8,5 9,5
Зона: 1
Зона: 3
Cu_кисл_лог
• М1=8,68;
М2=4,68;
df=47;
t=47,04;
P<0,0001.
18. t-тест Стьюдента для не связанных совокупностей
Два типа организации файла.Число измерений в группах может быть
разным.
Условия использования:
• Всего ДВЕ выборки;
• Нормальное распределение в каждой;
• Равенство дисперсий в двух выборках;
• n>10;
19. Сравнить две не связанные совокупности. Порядковая шкала или отклонение от нормального распределения
Число измерений вгруппах может быть
разным.
Условия
использования:
• Всего ДВЕ
сравниваемых
выборки;
• N<100;
20. Тест Манна-Уитни
Boxplot by GroupТест МаннаУитни
Variable: длина1
Exclude condition: Зона=2
26
24
22
20
18
длина1
16
14
12
10
8
6
4
2
0
1
3
Median
25%-75%
Min-Max
Зона
Me1=1,5; Me3=15,0; U(n1=24; n3=25)=0,00; P<0,0001.
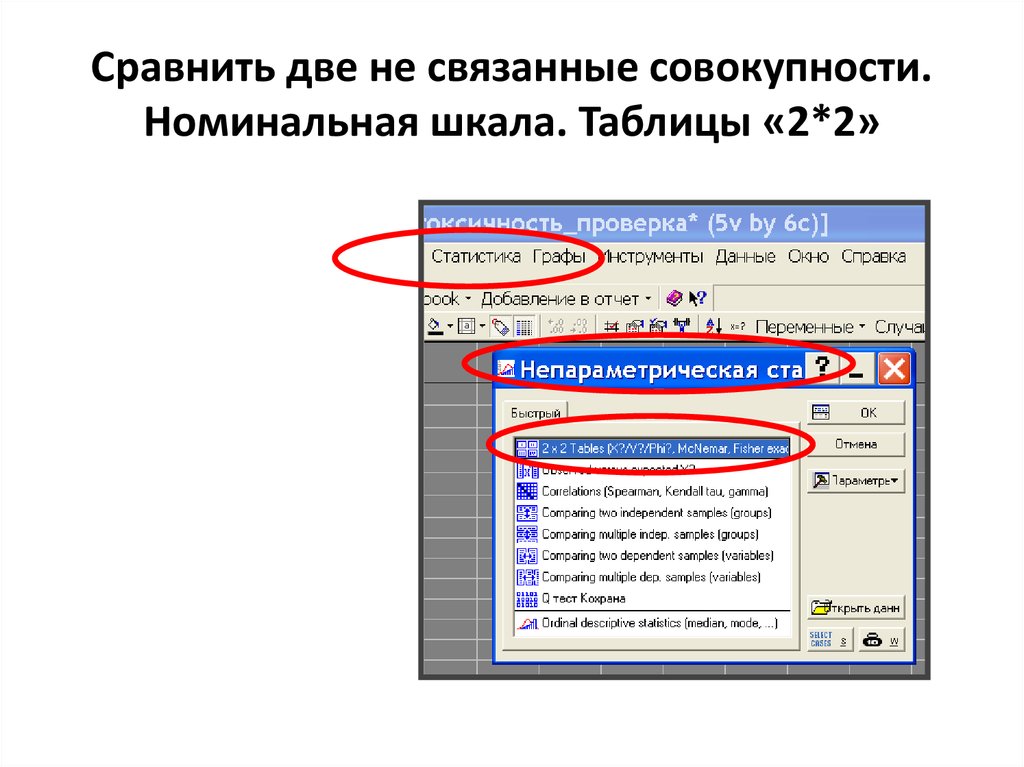
21. Сравнить две не связанные совокупности. Номинальная шкала. Таблицы «2*2»
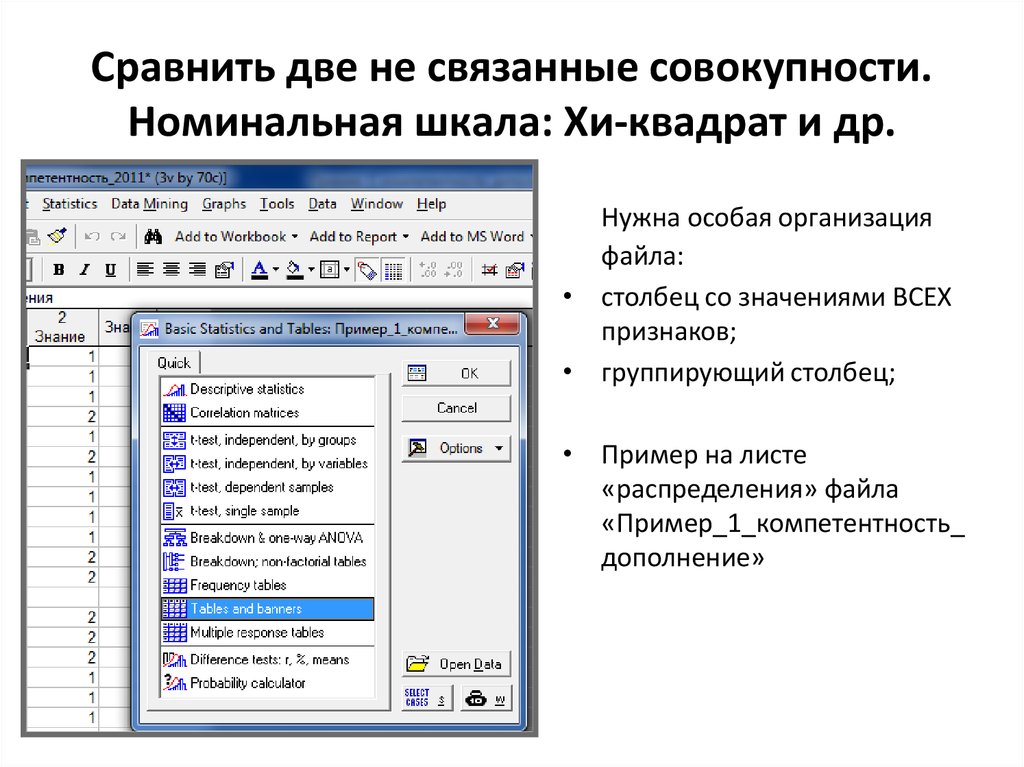
22. Сравнить две не связанные совокупности. Номинальная шкала: Хи-квадрат и др.
Нужна особая организацияфайла:
• столбец со значениями ВСЕХ
признаков;
• группирующий столбец;
• Пример на листе
«распределения» файла
«Пример_1_компетентность_
дополнение»
23. Сравнить две не связанные совокупности. Номинальная шкала: Хи-квадрат и др.
Categorized Histogram: Знание x Программа35
30
25
20
15
10
5
0
No of obs
Stat
SPSS
Stat
Знание: 1
Знание: 2
35
30
25
20
15
10
5
0
Stat
SPSS
SPSS
Знание: 3
Программа
24. Сравнить две не связанные совокупности. Номинальная шкала: Хи-квадрат и др.
• «Ручной» расчет в EXCEL:файл «Хи-квадрат2эмпирических.xls»
25. Выбор статистического теста при сравнении распределений (сравнении центральных тенденций)
ЗадачаКоличественная
шкала, нормальное
распределение
Порядковая шкала
или отклонение от
нормального
распределения
Номинальная шкала
t-тест Стьюдента для
одной выборки
Тест Вилкоксона
Тест хи-квадрат
Сравнить две не
связанные совокупности
t-тест Стьюдента для не
связанных
совокупностей
Тест Манна-Уитни
Тест Фишера (тест хиквадрат)
Сравнить две
связанные
совокупности
t-тест Стьюдента
для связанных
совокупностей
Тест Вилкоксона
Тест МакНеймера
Сравнить одну группу с
гипотетическим
значением
26.
Удельная активность стронция-90 в костной ткани
Удельная активность 90Sr в костной ткани
Apodemus uralensis
90
Сравнение трех выборок
(критерий Краскела-Уолиса) H (2,
N=55)=8.5, p=0.01
80
70
Попарное сравнение выборок
(критерий Манна-Уитни):
60
50
Линия 1 – линия 2: p=0.04
Линия 1 – линия 3: p=0.01
Линия 2 – линия 3: p=0.74
40
30
20
10
0
1
2
3
Линия
N=26
N=13
N=16
Median
25%-75%
Non-Outlier Range
Outliers
Extremes
Удельная активность 90Sr в костной
ткани малой лесной мыши составляет
29±2 Бк/г (указано среднее значение и
стандартная ошибка средней, N=55)
Модоров М.В., Селезнев А.А. Пространственно-временная изменчивость населения мелких млекопитающих и
демографической структуры их популяций в микромасштабе [презентация к выступлению на конференции]
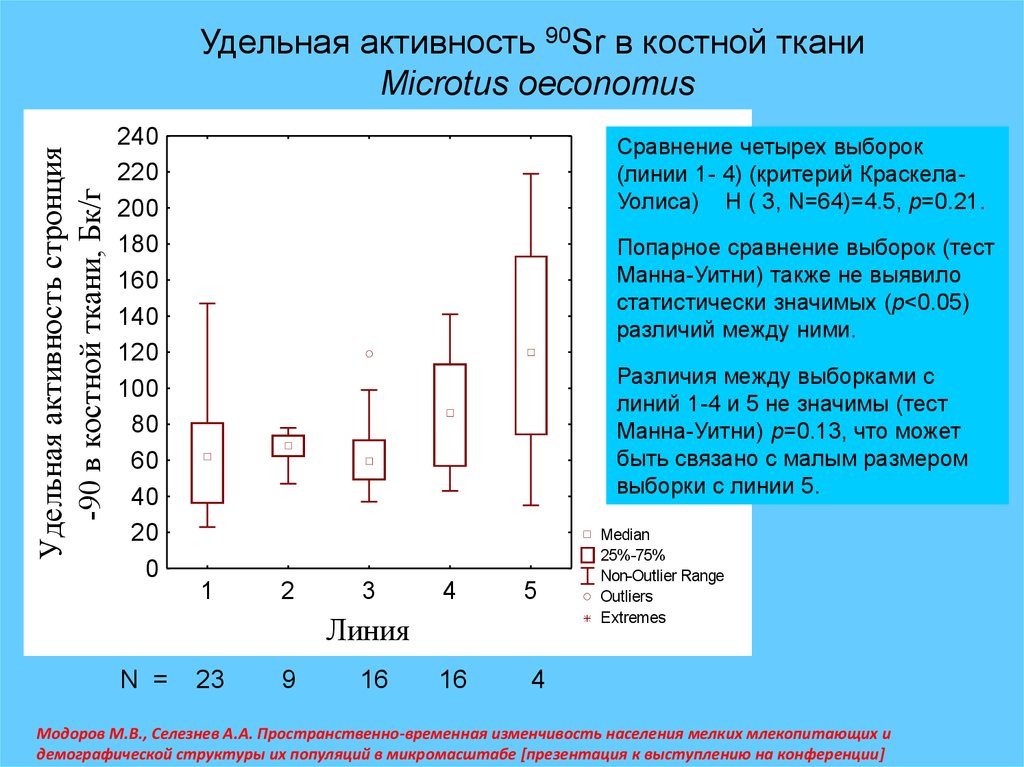
27.
Удельная активность стронция-90 в костной ткани, Бк/г
Удельная активность 90Sr в костной ткани
Microtus oeconomus
240
220
200
180
160
140
120
100
80
60
40
20
0
Сравнение четырех выборок
(линии 1- 4) (критерий КраскелаУолиса) H ( 3, N=64)=4.5, p=0.21.
Попарное сравнение выборок (тест
Манна-Уитни) также не выявило
статистически значимых (р<0.05)
различий между ними.
Различия между выборками с
линий 1-4 и 5 не значимы (тест
Манна-Уитни) р=0.13, что может
быть связано с малым размером
выборки с линии 5.
1
2
3
4
5
16
4
Линия
N =
23
9
16
Median
25%-75%
Non-Outlier Range
Outliers
Extremes
Модоров М.В., Селезнев А.А. Пространственно-временная изменчивость населения мелких млекопитающих и
демографической структуры их популяций в микромасштабе [презентация к выступлению на конференции]

















 Математика
Математика

![Парная] корреляция и регрессия. Типы статистических задач Парная] корреляция и регрессия. Типы статистических задач](https://cf.ppt-online.org/files/thumb/6/614SIOycEP9eC0HYjpAVUtBuvRiqKgGdmsFr7X.jpg)






