Похожие презентации:
Основы практической биомедицинской статистики
1. ОСНОВЫ ПРАКТИЧЕСКОЙ БИО-МЕДИЦИНСКОЙ СТАТИСТИКИ
ОСНОВЫ ПРАКТИЧЕСКОЙ БИОМЕДИЦИНСКОЙ СТАТИСТИКИСЕРИЯ 2
ПОНЯТИЕ ПЕРЕМЕННОЙ. ВИДЫ ПЕРЕМЕННЫХ. ТАБЛИЦЫ ДАННЫХ. ОПИСАТЕЛЬНАЯ
СТАТИСТИКА. ТАБЛИЦЫ ДАННЫХ И МАНИПУЛЯЦИИ С НИМИ В РАЗЛИЧНЫХ
СТАТИСТИЧЕСКИХ ПАКЕТАХ, ОБЗОР. ОПИСАТЕЛЬНАЯ СТАТИСТИКА В СТАТИСТИЧЕСКИХ
ПРОГРАММАХ. ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДАННЫХ.
2.
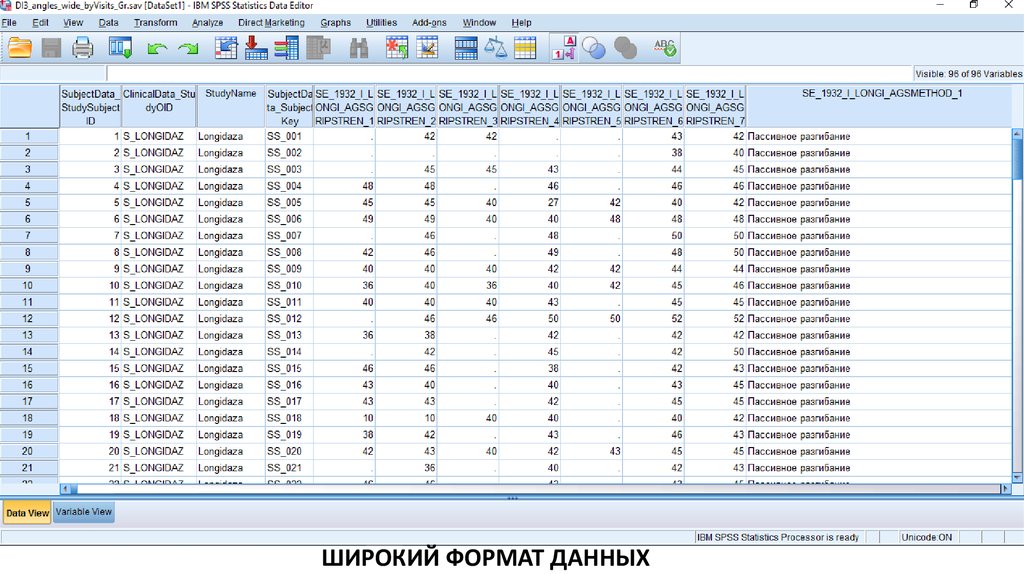
ШИРОКИЙ ФОРМАТ ДАННЫХ3.
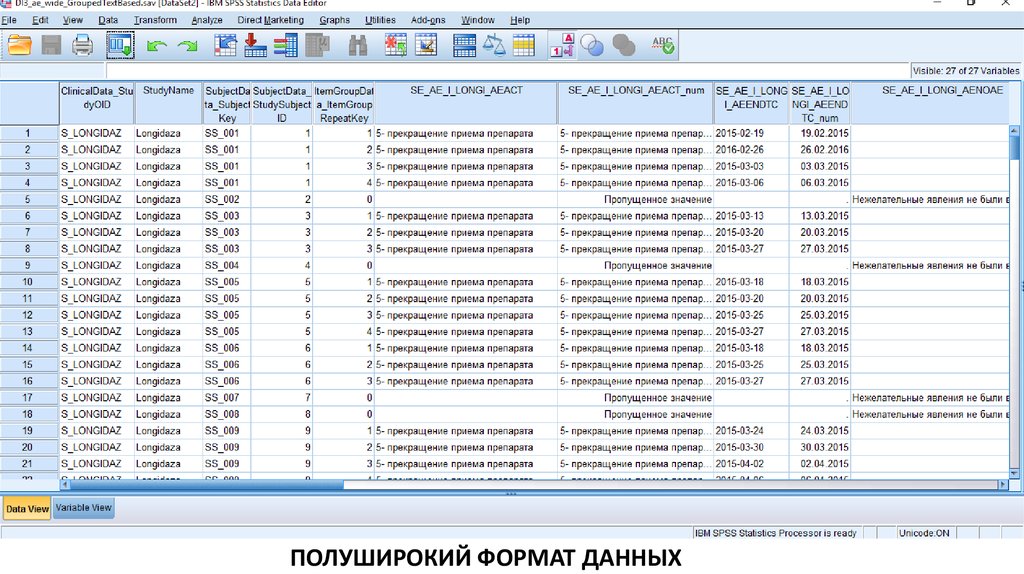
ПОЛУШИРОКИЙ ФОРМАТ ДАННЫХ4.
УЗКИЙ ФОРМАТ ДАННЫХ5. Типы переменных
Уменьшение объемаинформации
Типы переменных
• Количественные (интервальные) – возможны все
математические операции
• Дискретные (что то в штуках)
• Непрерывные (возраст, АД, пульс)
• Порядковые (ординальные) (стадия заболевания) можно сказать что больше-меньше
• Категориальные (качественные, номинальные) (цвета,
группа крови)
• Бинарные (выжил/умер, да/нет)
6. Для количественных переменных характерны выбросы данных
Oops!7. Тип шкалы: интервальная
Тип шкалыИнтервальная (измерение)
Примеры
АД, ЧСС, t°C, возраст...
Описательные статистики
Среднее арифметическое,
показатели дисперсии:
стандартное отклонение
Оценки
Среднее арифметическое +
ст.ошибка среднего
Тесты (inferential statistics) Зависят от характера
распределения
Сравнение 1 группы с
гипотетическим значением
Тест Вилкоксона/t-тест для одной
выборки
Сравнение 2 не связанных
совокупностей
Тест Манн-Уитни/t-тест для
несвязанных совокупностей
Сравнение 2 связанных
совокупностей
Тест Вилкоксона/t-тест для
связанных совокупностей
Сравнение 3 и более несвязанных
совокупностей
Тест Крускала-Уоллеса/1-way
ANOVA (дисперсионный анализ)
8. Тип шкалы: ординальная
Тип шкалыОрдинальная (порядковая)
Примеры
Функциональный класс
заболевания, оценка,
опросник и т.п.
Описательные статистики
Медиана, процентили, МКР
Оценки
Медиана + 95%
доверительный интервал
для медианы
Тесты (inferential statistics)
Сравнение 1 группы с
гипотетическим значением
Тест Вилкоксона
Сравнение 2 не связанных
совокупностей
Тест Манн-Уитни
Сравнение 2 связанных
совокупностей
Тест Вилкоксона
Сравнение 3 и более
несвязанных совокупностей
Тест Крускала-Уоллеса
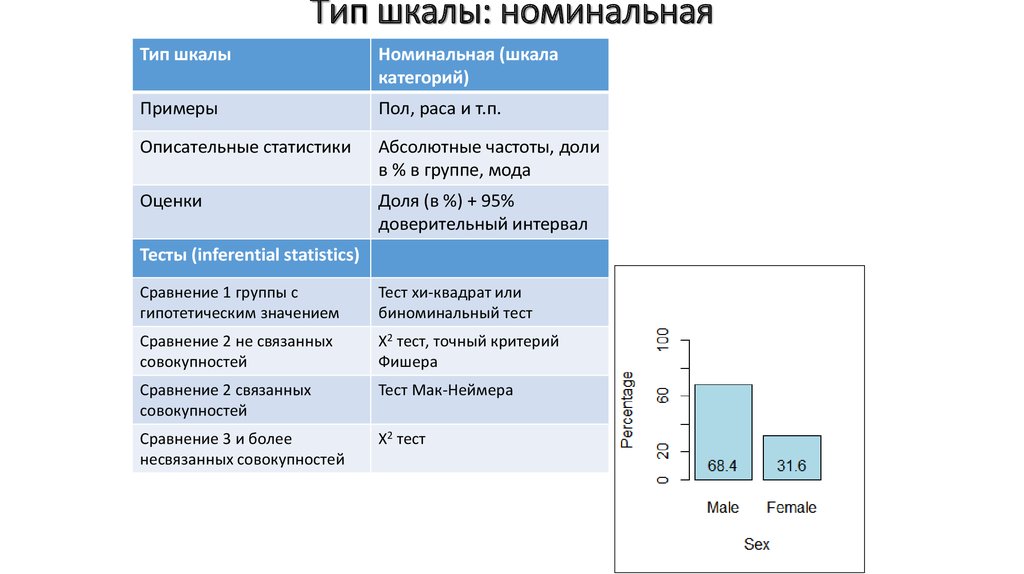
9. Тип шкалы: номинальная
Тип шкалыНоминальная (шкала
категорий)
Примеры
Пол, раса и т.п.
Описательные статистики
Абсолютные частоты, доли
в % в группе, мода
Оценки
Доля (в %) + 95%
доверительный интервал
Тесты (inferential statistics)
Сравнение 1 группы с
гипотетическим значением
Тест хи-квадрат или
биноминальный тест
Сравнение 2 не связанных
совокупностей
Χ2 тест, точный критерий
Фишера
Сравнение 2 связанных
совокупностей
Тест Мак-Неймера
Сравнение 3 и более
несвязанных совокупностей
Χ2 тест
10.
11.
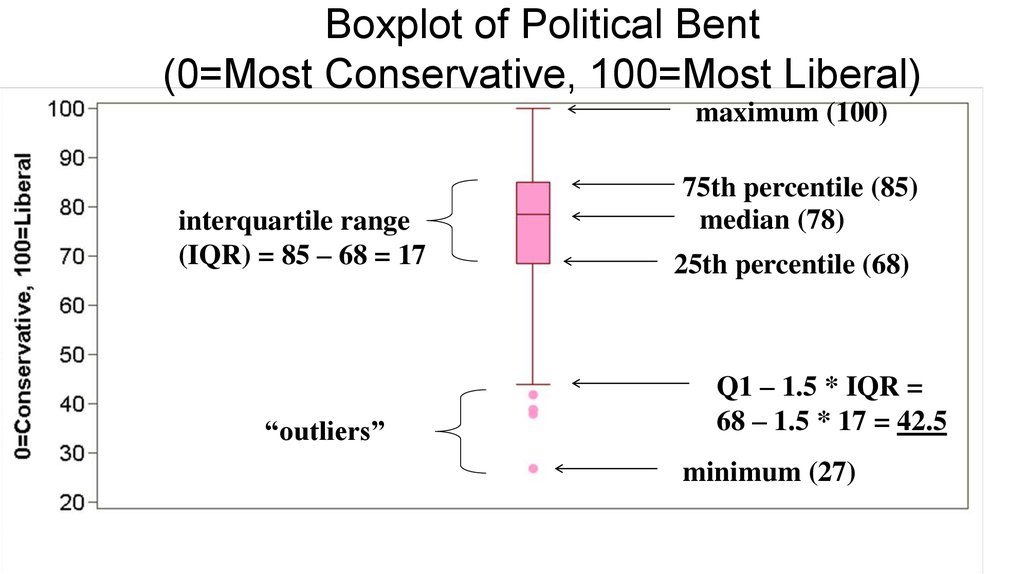
Boxplot of Political Bent(0=Most Conservative, 100=Most Liberal)
maximum (100)
interquartile range
(IQR) = 85 – 68 = 17
“outliers”
75th percentile (85)
median (78)
25th percentile (68)
Q1 – 1.5 * IQR =
68 – 1.5 * 17 = 42.5
minimum (27)
12.
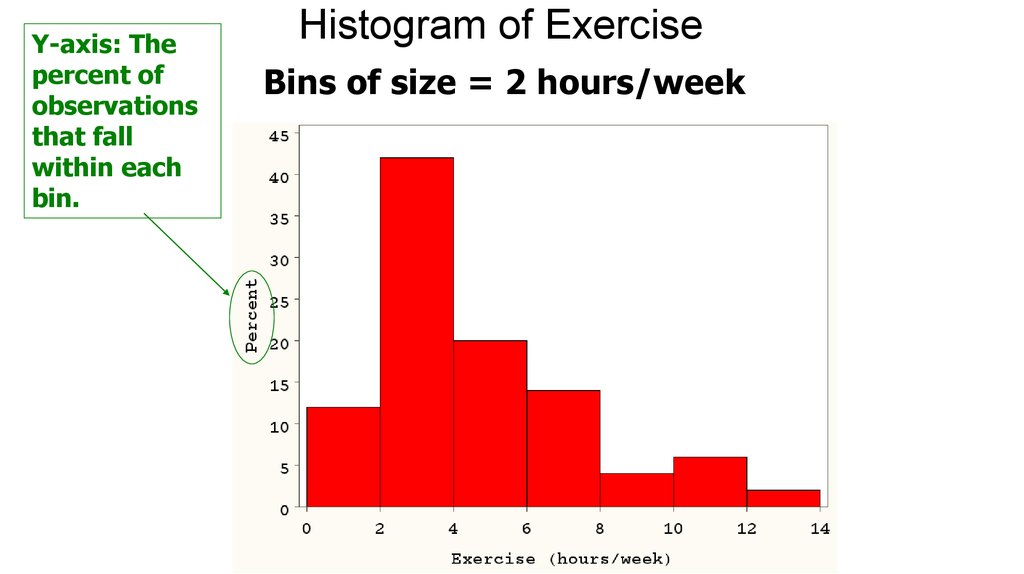
Y-axis: Thepercent of
observations
that fall
within each
bin.
Histogram of Exercise
Bins of size = 2 hours/week
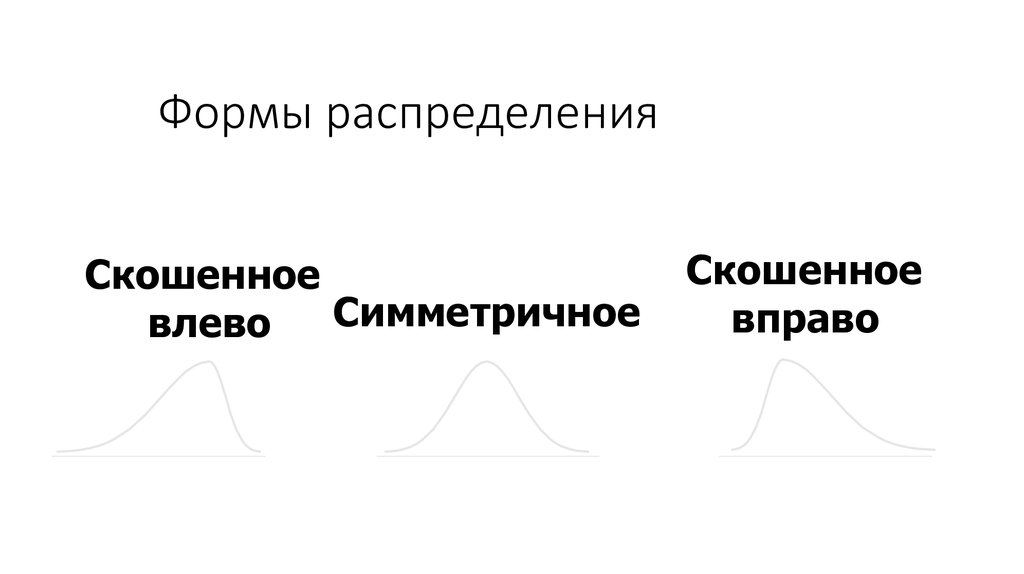
13. Формы распределения
СкошенноеСимметричное
влево
Скошенное
вправо
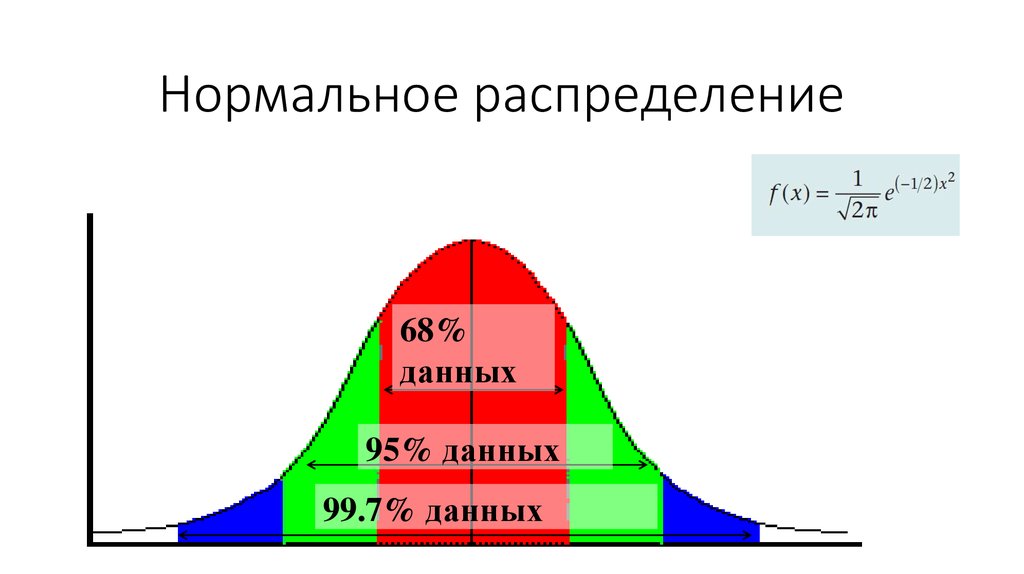
14. Нормальное распределение
68%данных
95% данных
99.7% данных
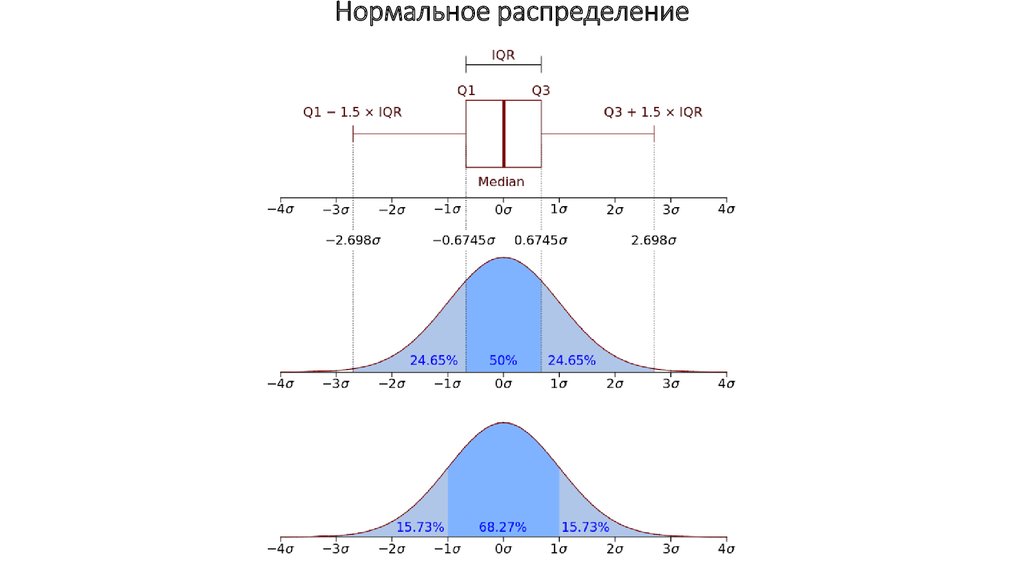
15. Нормальное распределение
16.
17.
18.
19.
20. Описательные статистики: меры центральной тенденции
среднее арифметическое (+ уникальность, + простота расчета, зависимость от экстремальных значений)медиана – значение, которое делит ряд данных пополам (+
уникальность, + простота расчета, + малая зависимость от
экстремальных значений, - интерпретация)
медиана=52
50 50 50 52 52 52 52 52 52 52 53
медиана =2
мода – наиболее часто встречающееся значение
21. Среднее
nСреднее
X
Пример:
x
i 1
n
i
x1 x2 xn
n
17 19 21 22 23 23 23 38
n
X
x
i 1
n
i
17 19 21 22 23 23 23 38
23.25
8
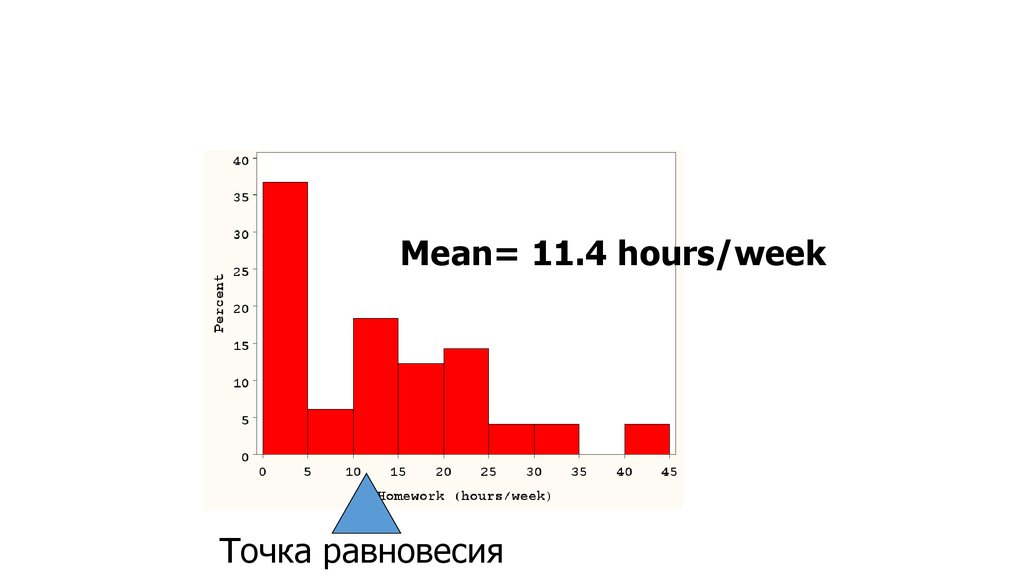
22.
Mean= 11.4 hours/weekТочка равновесия
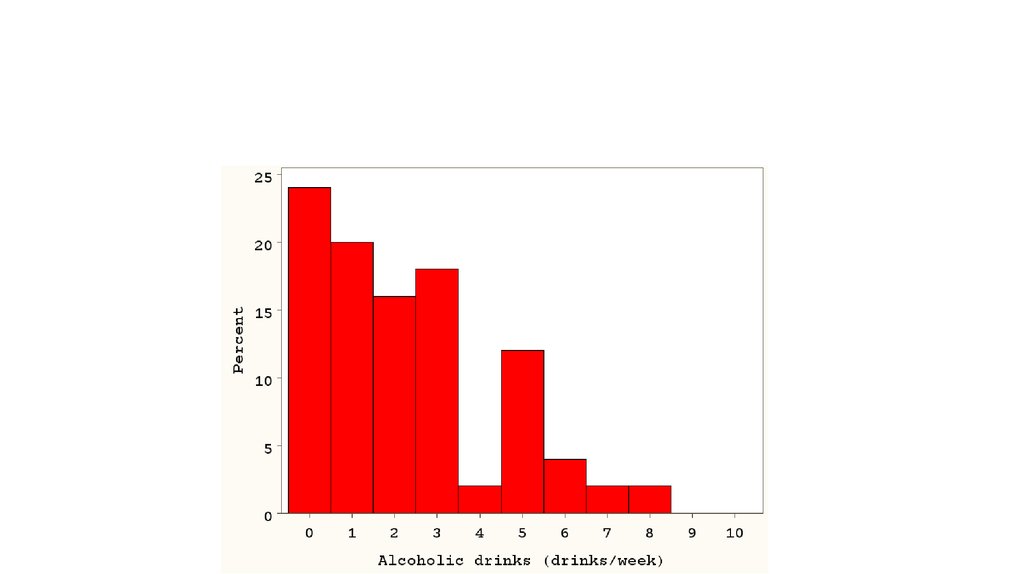
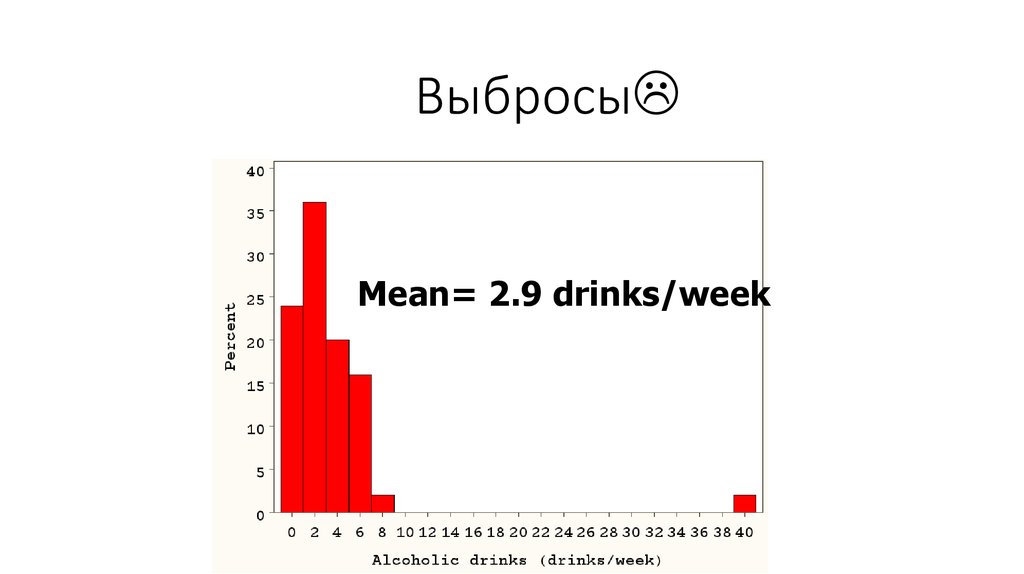
23. Выбросы
ВыбросыMean= 2.9 drinks/week
24. МЕДИАНА
• Значение в середине распределенияРасчет:
• Среднее если нечетное число
• Среднее между двумя средними числами если
четное.
25.
3025
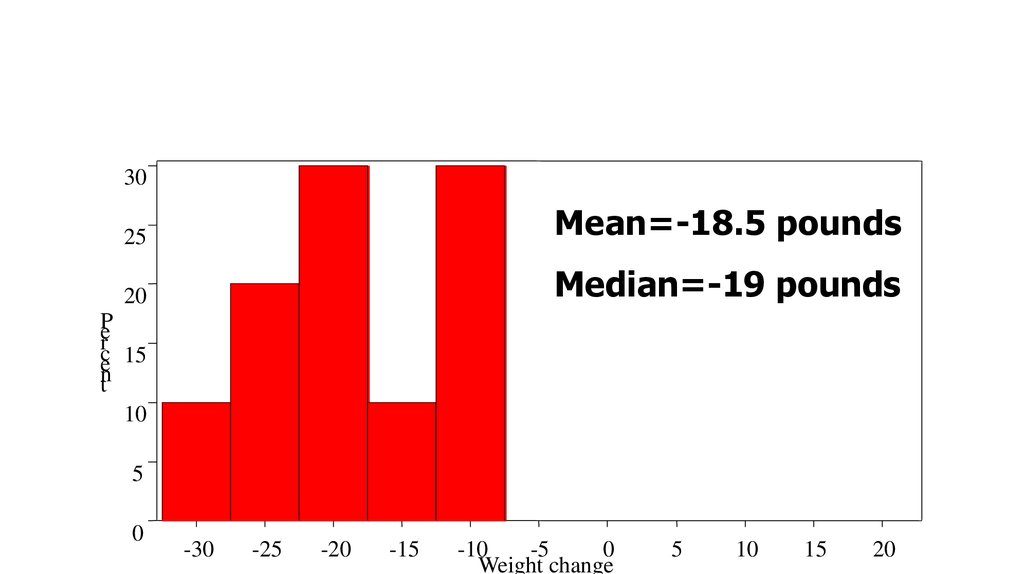
Mean=-18.5 pounds
20
Median=-19 pounds
P
er
ce 15
nt
10
5
0
-30
-25
-20
-15
-10
-5
0
Weight change
5
10
15
20
26.
3025
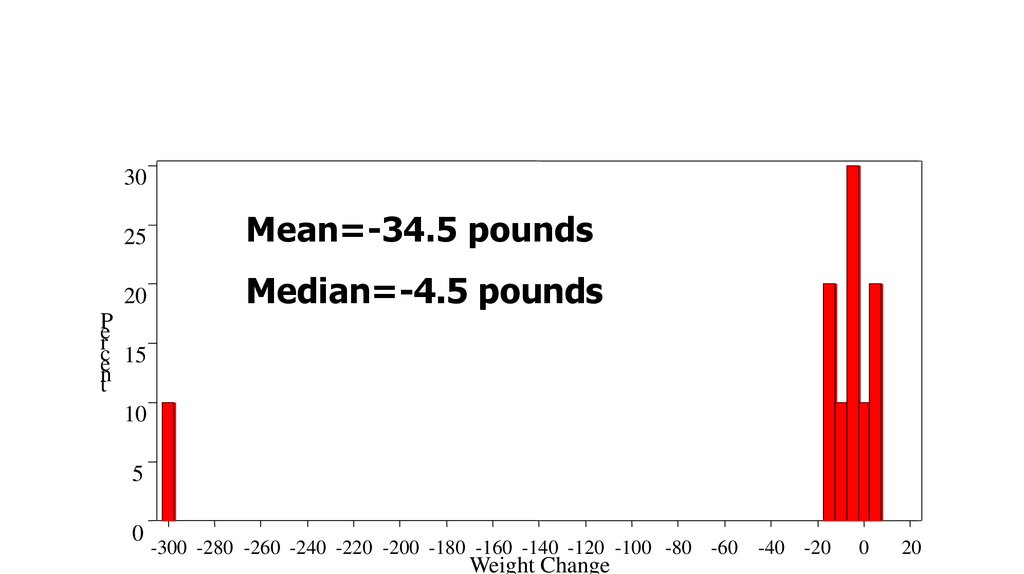
Mean=-34.5 pounds
20
Median=-4.5 pounds
P
er
ce 15
nt
10
5
0
-300 -280 -260 -240 -220 -200 -180 -160 -140 -120 -100 -80 -60
Weight Change
-40 -20
0
20
27. Меры разброса данных Меры рассеяния показывают, насколько хорошо данные значения представляют данную совокупность
• Размах• Стандартное отклонение
• Перцентили
• Межквартильный размах (IQR)
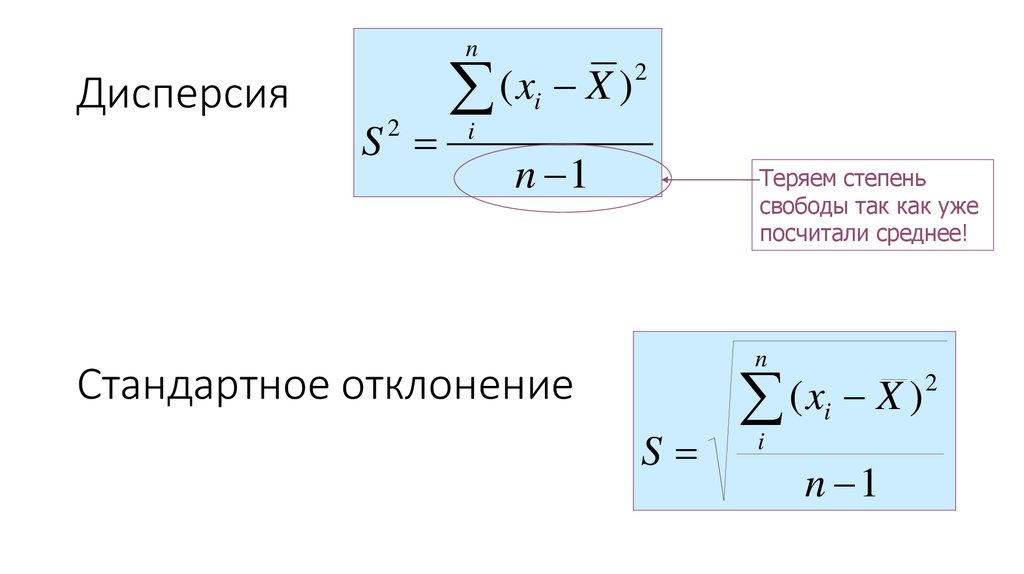
28. Дисперсия
nДисперсия
S
2
(x X )
2
i
i
n 1
Теряем степень
свободы так как уже
посчитали среднее!
n
Стандартное отклонение
S
(x X )
i
i
n 1
2
29.
Mean = 15S = 0.9
Mean = 15
S = 3.7
Mean = 15
S = 5.1
30. Стандартное отклонение и стандартная ошибка среднего
• Отклонение – это разброс данных• Ошибка – оценка истинного значения параметра, который
рассчитывается ИСКУССТВЕННО
НЕ ПУТАТЬ!
31. Межквартильный размах
• Межквартильный размах = 3-й квартиль – 1-й квартиль• Средние 50% данных
• Выбросы не влияют!
32.
33.
34.
Окно свойств переменных SPSS35.
36.
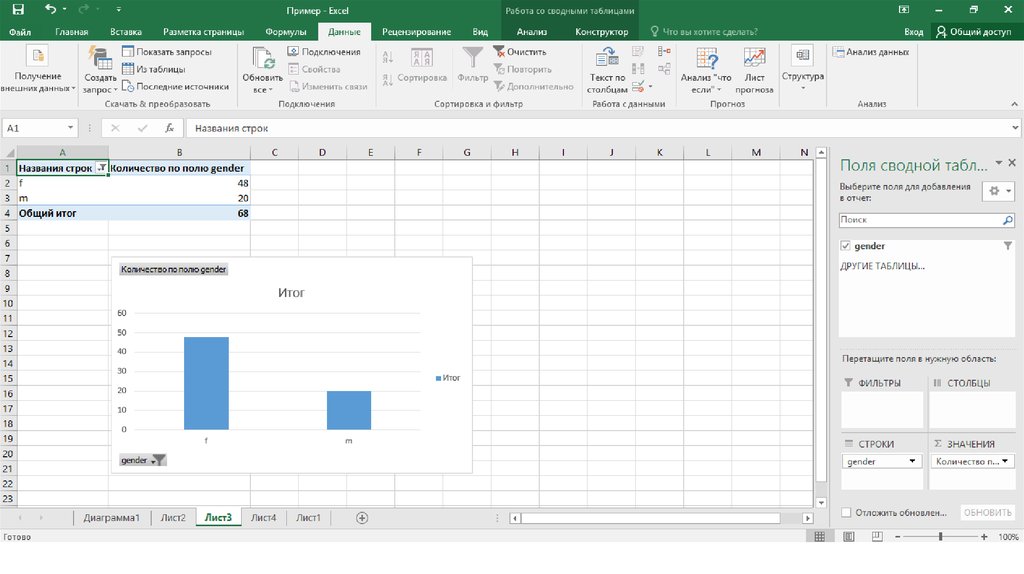
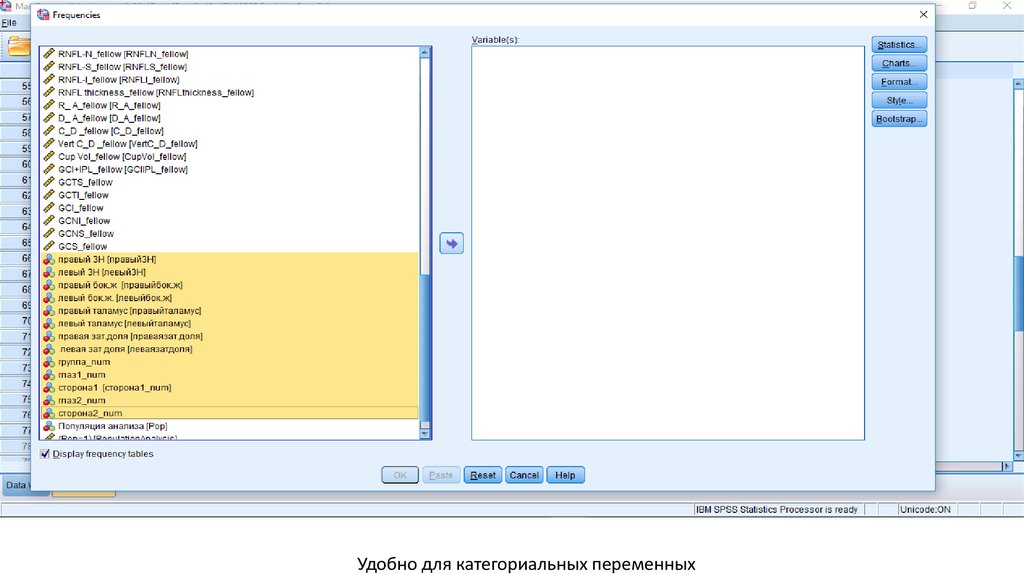
Удобно для категориальных переменных37.
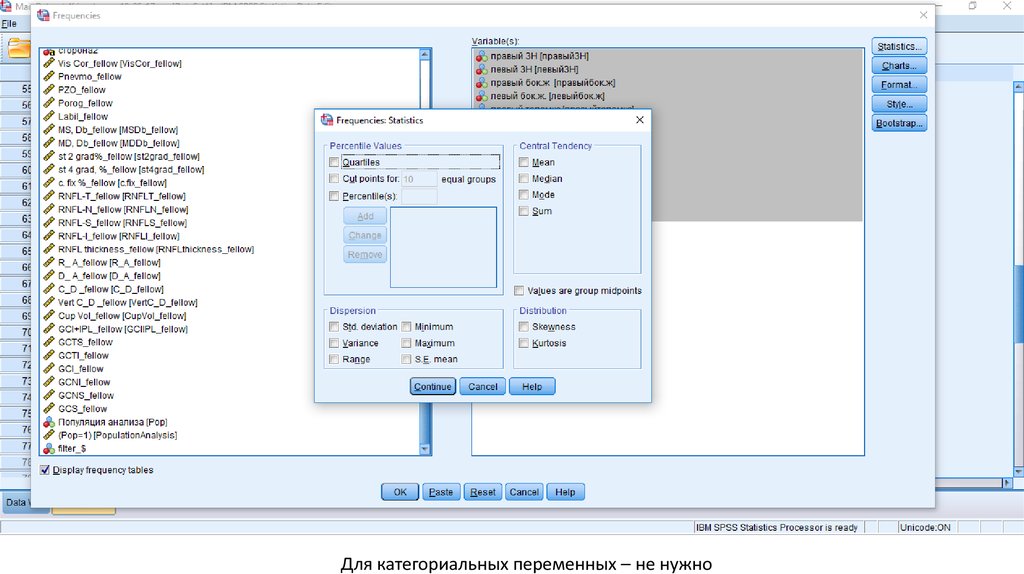
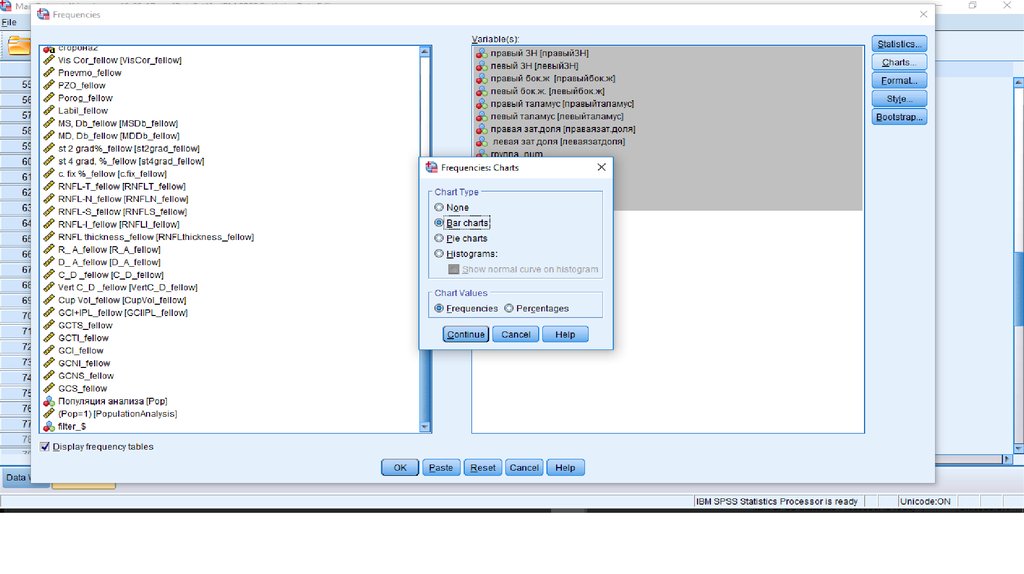
Для категориальных переменных – не нужно38.
39.
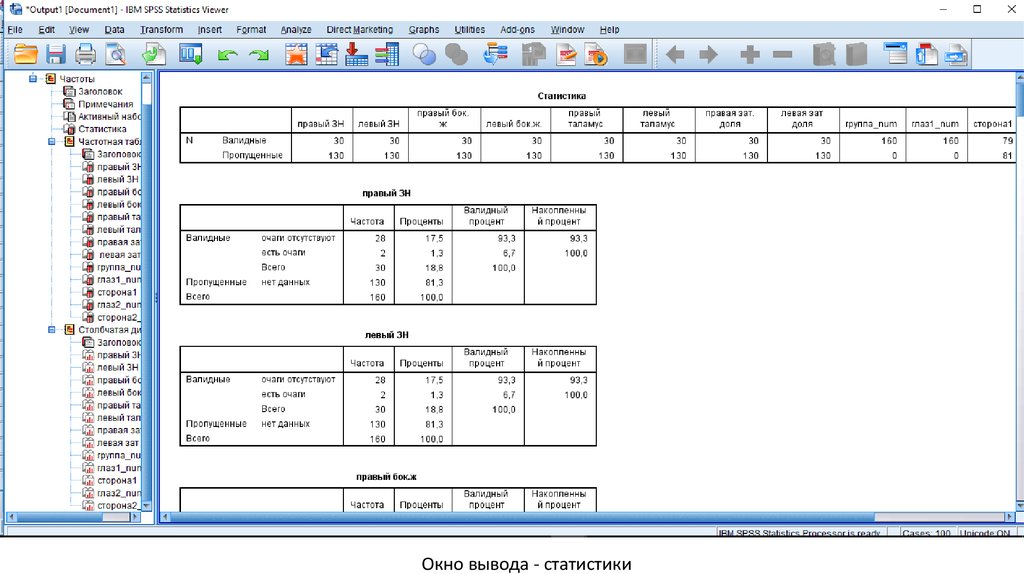
Окно вывода - статистики40.
Окно вывода - графики41.
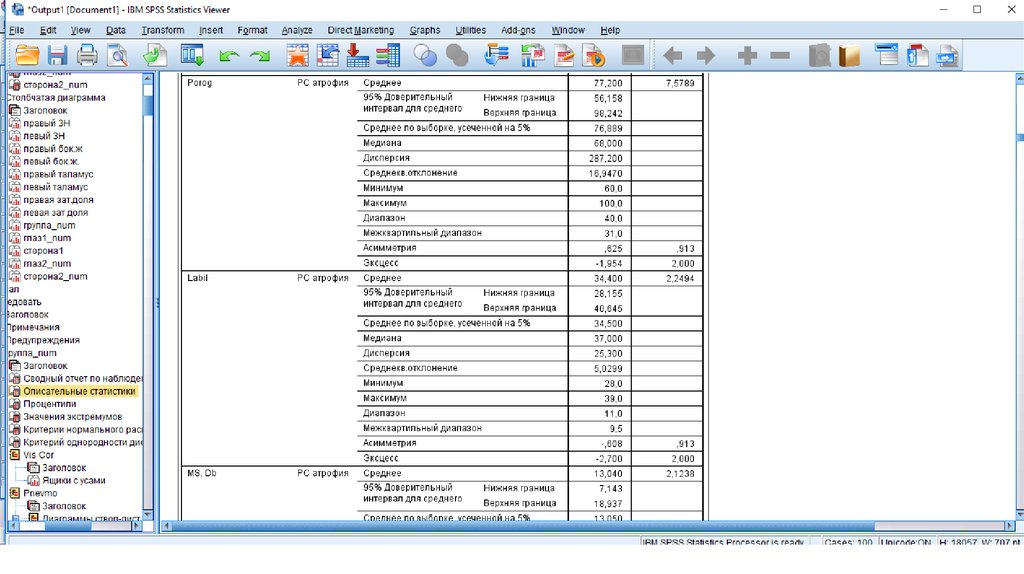
Статистики для количественных переменных, но есть более удобное окно42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
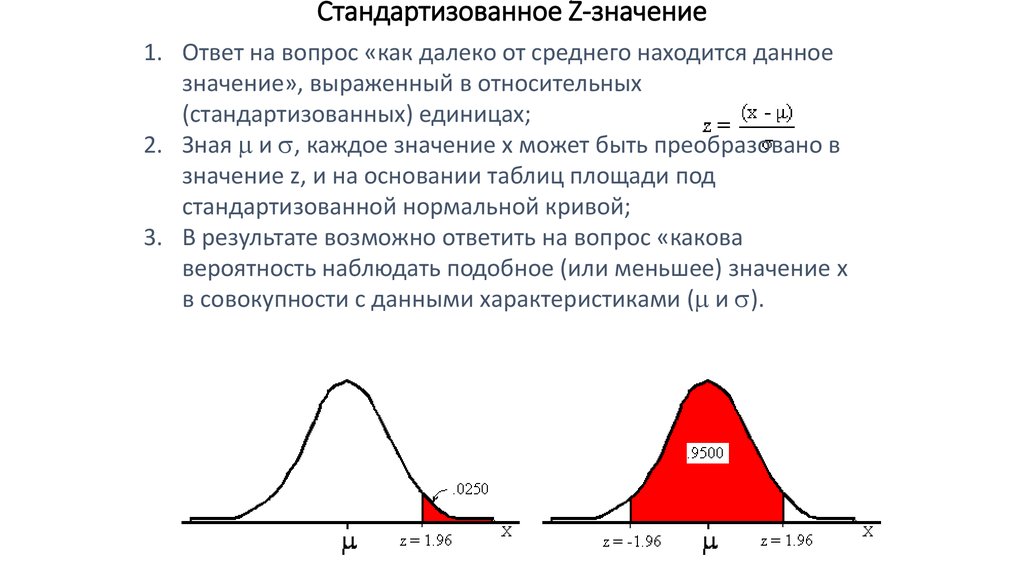
52. Стандартизованное Z-значение
1. Ответ на вопрос «как далеко от среднего находится данноезначение», выраженный в относительных
(стандартизованных) единицах;
2. Зная m и s, каждое значение х может быть преобразовано в
значение z, и на основании таблиц площади под
стандартизованной нормальной кривой;
3. В результате возможно ответить на вопрос «какова
вероятность наблюдать подобное (или меньшее) значение x
в совокупности с данными характеристиками (m и s).
53. Оценка среднего по выборочному среднему
Приблизительно 95% получаемых x̅ будут находится в пределах2 стандартных отклонений от среднего полученных выборочных
средних, этот интервал будет ограничен:
Поскольку µ и µx̅ неизвестны по условиям задачи, x̅ используется
в качестве точечной оценки µ, и 95% построенных интервалов
будут содержать µ. В общем случае доверительный интервал:
Z-значение в данном случае называется коэффициент
надежности (reliability coefficient), а закрашенная площадь 1-α –
доверительный уровень (confidence level)
54. Общая формула для оценки интервала
• оценка ± коэффициент надежности ∗(стандартная ошибка)
55. Интерпретация доверительных интервалов
На примере 95% ДИ для среднего:• Интервальная оценка μ вычисляется по
формуле:
• Если α=0.05, мы можем сказать, что при
повторном отборе выборки, 95% полученных
интервалов будут включать μ. Это заключение
основано на вероятности получения
различных значений x̅.
56. Доверительные интервалы
• Многими незаслуженно относятся к описательнойстатистике
• ДИ – численный интервал, построенный вокруг
оценки параметра по определенной методике
• В силу этого он характеризует, в первую очередь,
методику
• Во вторую очередь он характеризует данные
• В последнюю очередь – параметры
популяционного показателя
57. Исследователь Петрик рапортует:
95% доверительный интервалдля среднего
0,1-0,4!
Robust misinterpretation of confidence intervals. Hoekstra R1, Morey RD, Rouder JN,
Wagenmakers EJ. Psychon Bull Rev. 2014 Jan 14.
58. Какие из приведенных утверждений верны:
95% ДИ 0,1-0,4!1. Вероятность, что истинное (популяционное) среднее больше 0,
как минимум, 95%
2. Вероятность, что истинное среднее равно 0 меньше 5%
3. Нулевая гипотеза, что истинное среднее равно 0, вероятно, будет
отвергнута
4. С 95% вероятностью истинное среднее находится между 0,1 и 0,4
5. Мы можем быть на 95% уверены, что истинное среднее
находится между 0,1 и 0,4
6. Если бы мы повторяли эксперимент снова и снова, 95% времени
истинное среднее находилось бы в интервале 0,1 – 0,4
59. Доверительные интервалы: ответы
1.Вероятность, что истинное (популяционное) среднее больше 0, как
минимум, 95%
2.
Вероятность, что истинное среднее равно 0 меньше 5%
• Присвоение вероятности параметру
3.
Нулевая гипотеза, что истинное среднее равно 0, вероятно, неверна
• Присвоение вероятности гипотезе
4.
С 95% вероятностью истинное среднее находится между 0,1 и 0,4
• Присвоение вероятности параметру
5.
Мы можем быть на 95% уверены, что истинное среднее находится
между 0,1 и 0,4
6.
Если бы мы повторяли эксперимент снова и снова, 95% времени
истинное среднее находилось бы в интервале 0,1 – 0,4
• Утверждение относительно границ истинного среднего
7.
Если бы мы повторяли эксперимент снова и снова, 95% времени (в 95%
случаев) доверительные интервалы содержали бы истинное среднее
































 Математика
Математика Информатика
Информатика








