Двойные интегралы

1.

2.

Пусть D – замкнутая и ограниченная область на
плоскости
XOY
и
в
ней
определена
произвольная ограниченная функция z=f(x,y).
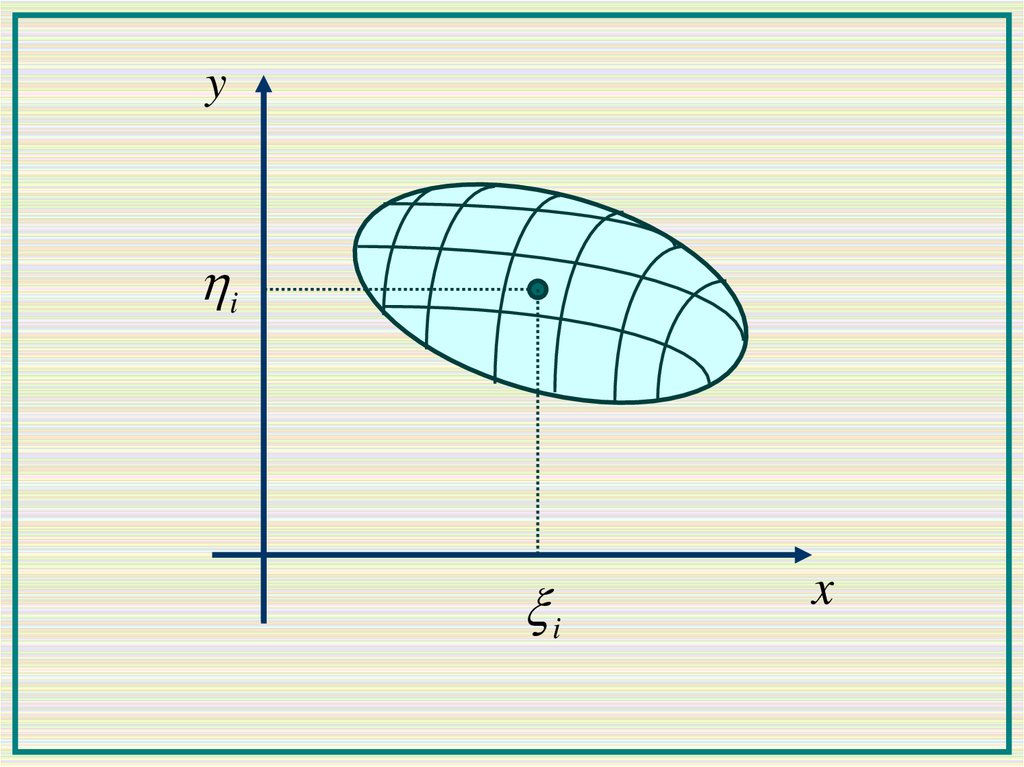
Разобьем область D сетью кривых на n
произвольных частей Di с площадями ΔSi.
В каждой из областей Di выберем точку (ξi,ηi).

3.

y
i
i
x

4.

Сумму вида
n
f ( i , i ) Si
i 1
называют интегральной суммой
для функции z=f(x,y) в области D.
1

5.

Интегральная сумма зависит от способа
разбиения отрезка и выбора точек (ξi, ηi).
Диаметром d области D называется наибольшее
расстояние между граничными точками этой
области.
Пусть max d – наибольший из всех диаметров
частичных областей. Тогда

6.

Если
существует
конечный
предел
интегральной суммы при max d 0
не зависящий от способа разбиения
области D и выбора точек (ξi, ηi), то он
называется двойным интегралом от
функции z=f(x,у) по области D.
n
lim
max d 0
f ( , ) S f ( x, y)dS
i 1
i
i
i
D

7.

Функция z=f(x,у) называется интегрируемой
в области D.
Область D называется областью
интегрирования.
х, у – называются переменными
интегрирования.
dS dxdy
- элемент площади.

8.

Если функция f(x,y) непрерывна
в замкнутой ограниченной
области, то она интегрируема
в этой области.