Похожие презентации:
Двойной интеграл. Приложения двойного интеграла
1.
Двойной интеграл. Приложениядвойного интеграла.
Двойной интеграл. Его свойства.
Геометрический смысл.
Вычисление двойного интеграла.
2.
Определение двойного интеграла.• Пусть функция z f ( x, y ) определена в области D.
Разобьём область D произвольным образом на связные
части Di, i 1, n. В каждой из частей выберем
произвольным образом точку M i i , i , M i D i , i 1, n.
Пусть i - площадь подобласти Di, max d i , i 1, n .
i 1,n
После чего составим
интегральную сумму:
(*)
Если существует конечный предел интегральных сумм (*)
при 0 (n ) , nкоторый не зависит от способа
разбиения области D Di и от выбора точек M i D i ,
i 1
то он называется
двойным интегралом функции по области D и
3.
Существование двойного интегралаи обозначается:
Функция, z f ( x, y )
для которой
двойной интеграл
существует, называется интегрируемой в области D.
Пусть граница Г области D является кусочно-гладкой
линией, т.е. её можно представить в виде конечного числа
гладких участков кривых, т.е. линий, имеющих касательную
в каждой своей точке.
Теорема 1: Если функция z f ( x, y ) непрерывна в замкнутой
ограниченной области, то для неё существует двойной
интеграл.
4.
Свойства двойного интеграла1.
Если функции: f ( x, y ), g( x, y ) - интегрируемы в области D
то их сумма: f ( x, y ) g( x, y )также интегрируема в этой
области и верно равенство:
2.
Если функция z f ( x, y ) интегрируема в области D , то
функция z k f ( x, y ) - также интегрируема в этой
области (k const) и
Если функция z f ( x, y )
непрерывна в области D
и D D1 D 2 D n
3.
5.
Геометрический смысл двойногоинтеграла
Пусть функция
существует двойной интеграл:
тогда:
и для неё
где V- объём цилиндрического тела, у которого основанием
служит проекция поверхности
на плоскость
xOy, тело ограничено сверху поверхностью
.
6.
Вычисление двойного интеграла вд.с.к.
• Вычисление двойного интеграла сводится к повторному
интегрированию. Пусть областью изменения независимых
переменных является:
a x b
D
это криволинейная трапеция
y 1 ( x) y y 2 ( x)
на плоскости xOy ( y y 1 ( x), y y 2 ( x) - гладкие линии).
Тогда:
При этом область интегрирования должна быть
правильной в направлении оси Oy. Интеграл по
переменной «y» называется внутренним, а по переменной
«x»- внешним.
7.
Вычисление двойного интеграла вд.с.к.
• Сначала вычисляется внутренний
интеграл и в результате
y2 (x)
получаем некоторую функцию
затем
f ( x, y )dy ( x )
интегрируя её по другой
y1 ( x )
b
переменной «x», получаем результат:
(x)dx f (x, y )dxdy
при этом последний интеграл
a
D
называется внешним.
• Замечание 1: Пределы интегрирования будут постоянными
в обоих интегралах, если область интегрирования есть
квадрат или прямоугольник со сторонами параллельными
осям координат (в д.с.к.).
• Замечание 2: Если область интегрирования есть
правильная область в направлении оси Ox, то
c y d
D
x1 ( y ) x x 2 ( y )
8.
Вычисление двойного интеграла вд.с.к.
• Тогда соответствующий двойной интеграл:
• Замечание 3: Если область интегрирования D не
является правильной ни в одном из координатных
направлений, то её представляют в виде суммы конечного
числа областей, каждая из которых правильная по одному
из направлений Ox либо Oy, затем используя свойства
двойного интеграла, производят непосредственно
вычисления.
9.
Пример 1:• Вычислить значение двойного интеграла:
в области D : ABC A(0,0), B( 2,0), C( 2,1)
Данная область является правильной
в обоих направлениях. Поэтому:
2
2
x
ydxdy
D
y x / 2
x y dxdy dx x ydy
2
2
D
0
y 0
2
2
x
1
4
x 2 0 dx x 4dx
80
5
8
0
2
или:
1
x 2
0
x 2 y
2
x
y
dxdy
dy
x
ydx
2
D
x 2
1
1
x3
8
8 4
8 y2 y5
4
ydy y y dy
3 x 2 y
3
3
3 2
5 0 5
0
0
1
10.
Пример 2:• Изменить порядок интегрирования в двойном интеграле:
1
x
. Изобразим область интегрирования:
dx f (x, y )dy
0
x
2
1
x y
0
x y
0 x 1
D 2
x y x
dy f (x, y )dx
Замечание 4: Пределы интегрирования необходимо
расставлять так, чтобы процесс вычисления был наименее
трудоёмким.
11.
Пример 3:• Не вычисляя двойного интеграла, выяснить, который из
них имеет большее значение:
( x y )dxdy
D
или ( x y ) 2 dxdy
D
Где область D задана своими границами:
x 0; y 0; x y 1
В области D имеем:
f1 ( x, y ) 1, f 2 ( x, y ) ( x y ) 2 ( x y )
т.е. первый имеет большее значение, т.к. для него функция
больше.
12.
Несобственныеинтегралы.















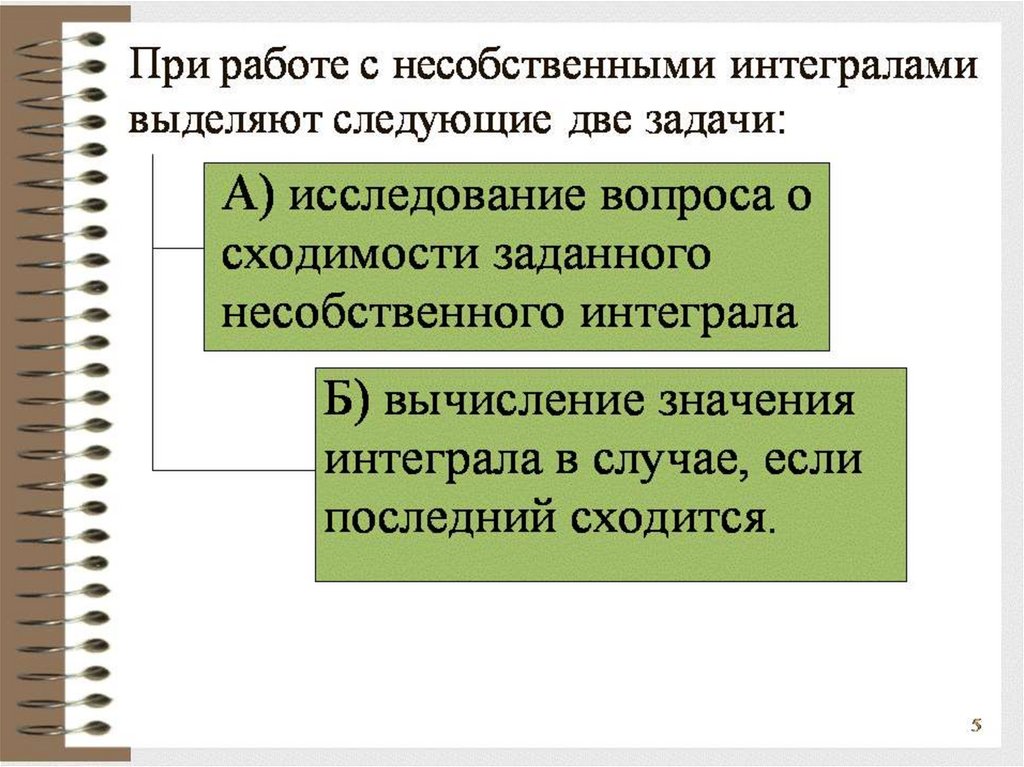
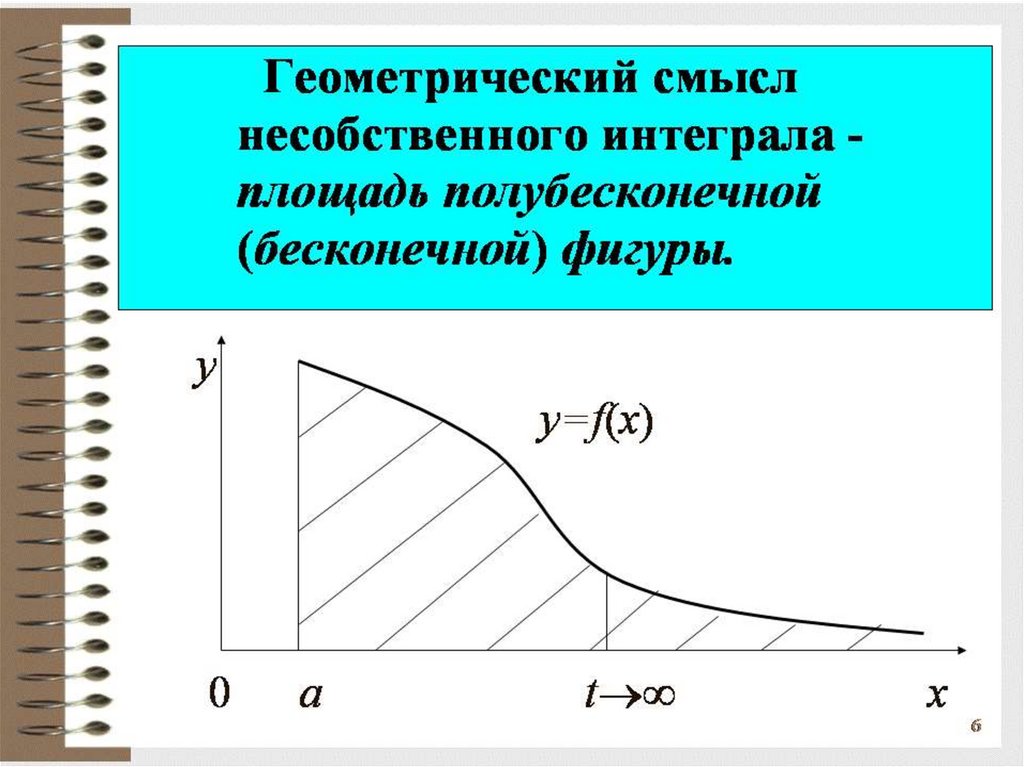








 Математика
Математика








