Геометрическая интерпретация ЗЛП

1. Геометрическая интерпретация ЗЛП

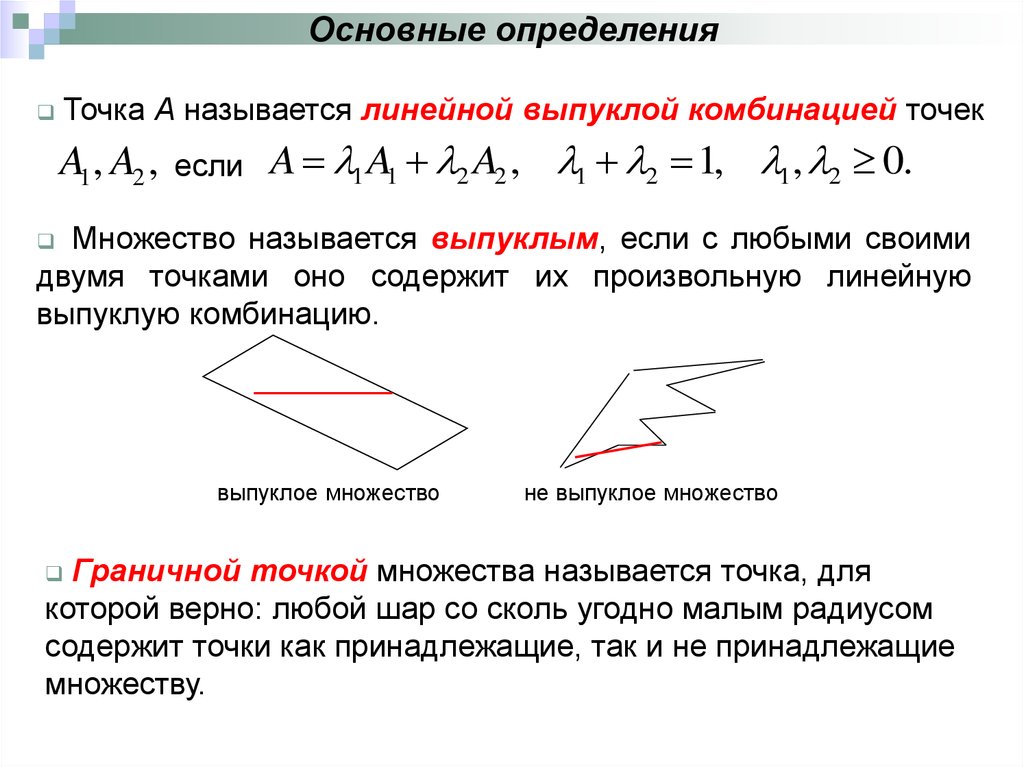
2. Основные определения

Точка А называется линейной выпуклой комбинацией точек
A1 , A2 ,
если
A 1 A1 2 A2 , 1 2 1, 1, 2 0.
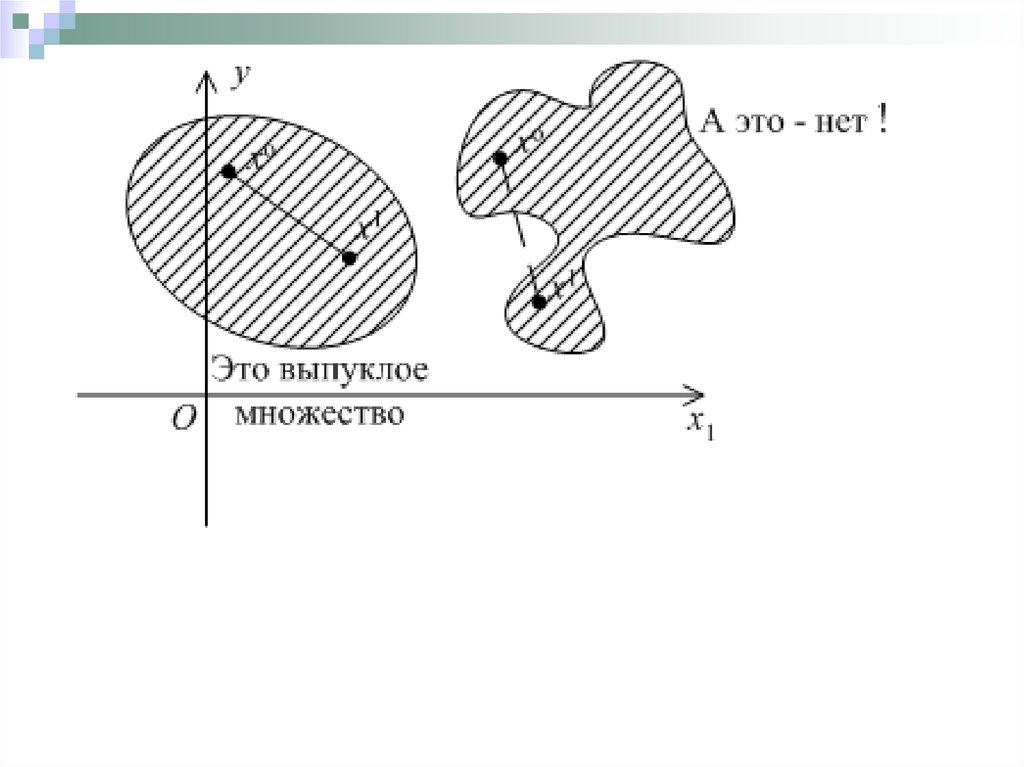
Множество называется выпуклым, если с любыми своими
двумя точками оно содержит их произвольную линейную
выпуклую комбинацию.
выпуклое множество
не выпуклое множество
Граничной точкой множества называется точка, для
которой верно: любой шар со сколь угодно малым радиусом
содержит точки как принадлежащие, так и не принадлежащие
множеству.

3.

4.

5.

Множество называется замкнутым, если оно содержит
все свои граничные точки.
Множество называется ограниченным, если существует
шар, радиусом R, содержащий в себе всё множество.
Точка называется угловой, если она не может быть
представлена в виде выпуклой линейной комбинации двух
различных точек этого множества.
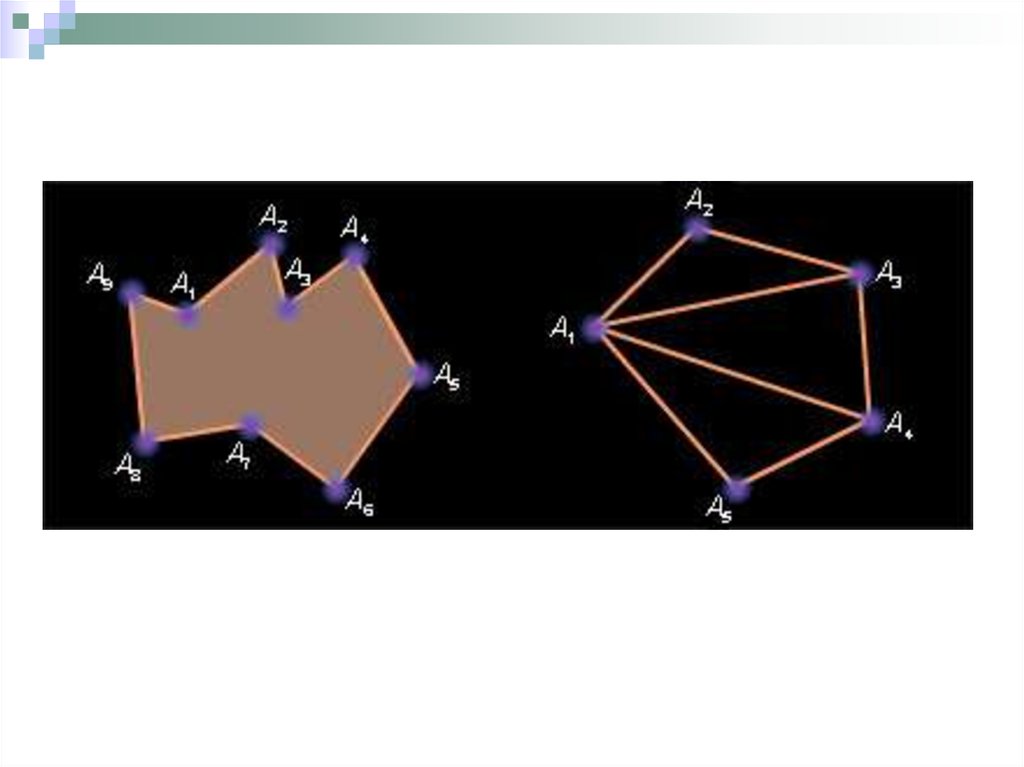
Ограниченное выпуклое замкнутое множество на плоскости
с конечным числом вершин называется выпуклым
многоугольником.

6.

Теорема Выпуклый замкнутый ограниченный
многогранник является выпуклой линейной
комбинацией своих угловых точек.
Лемма Пересечение любого количества
выпуклых множеств является выпуклым
множеством.

7. Доказательство

Докажем, что любая точка треугольника удовлетворяет теореме. В
треугольнике A1А2А3 (рис.2.3) возьмем произвольную точку А4
и через нее проведем отрезок А1А4.
Так как точка А принадлежит отрезку А1А4, то она — выпуклая
линейная комбинация его концов, т. е.
А = t1A1 + t4А4, t1 0, t4 0,
t1 + t4 = 1.
(2.46)
Точка А4 принадлежит отрезку А2А3, следовательно, является
выпуклой линейной комбинацией его концов, т. е.
А4 = t2А2 + t3А3, t2 0, t3 0, t2 + t3 = 1.
(2.47)
Подставляя (2.47) в (2.46) получаем
А = t1A1 + t4(t2А2 + t3А3) = t1А1 + t2t4А2 + t3t4А3.
Полагая t1 = 1, t2t4 = 2, t3t4 = 3, окончательно имеем
А = 1А1 + 2А2 + 3А3,
1 0, 2 0, 3 0, 1 + 2 + 3 = 1,
(2.48)
т. е. точка А — выпуклая линейная комбинация вершин А1, А2, А3.
В выпуклом многоугольнике, имеющем n вершин (n > 3), добавляя
к правой части соотношения (2.48) остальные n - 3 вершины,
умноженные на нуль, окончательно получим
А = 1А1 + 2А2 + 3А3 + 0 А4 + ... + 0 Аn,
I 0 (i = 1, 2, ..., n), ,
т. е. точка А — выпуклая линейная комбинация угловых точек
многоугольника.

8. Геометрическая интерпретация задач линейного программирования

z c1 x1 c2 x2 min(max)
z (c1, c2 )
a11 x1 a12 x2 b1
a x a x b
21 1 22 2
2
..........
..........
........
am1 x1 am 2 x2 bm
x1 , x2 0

9.

10.

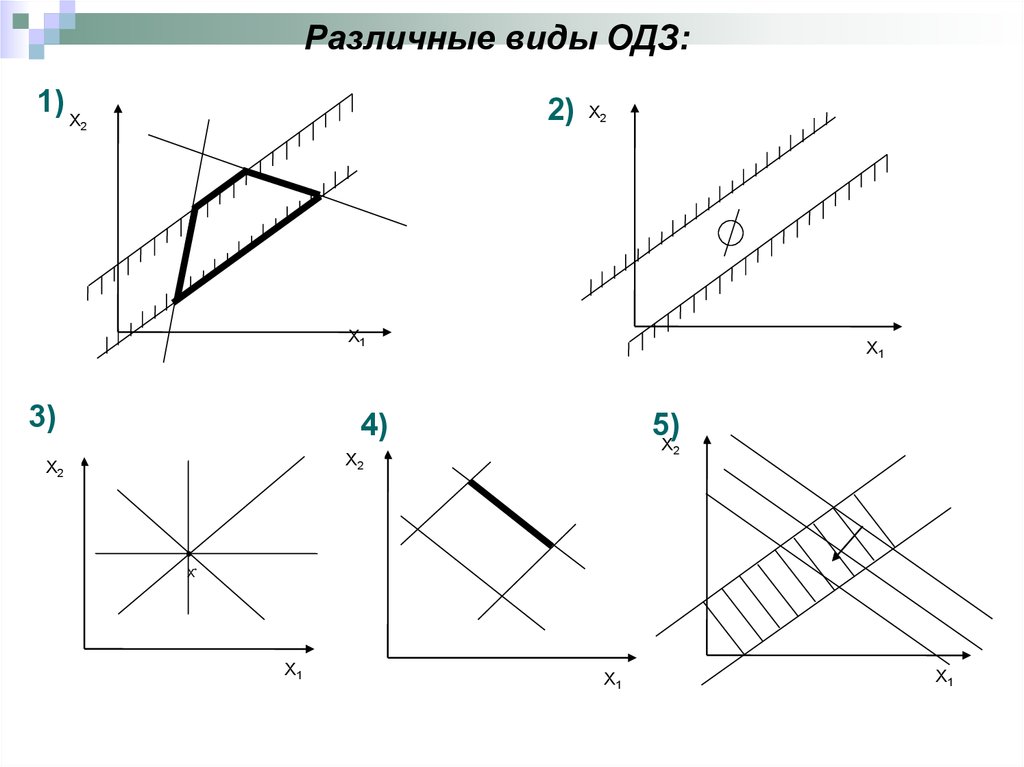
Различные виды ОДЗ:
1) X
2)
2
X2
X1
3)
X1
4)
5)
X
2
X2
X2
X*
X1
X1
X1

11.

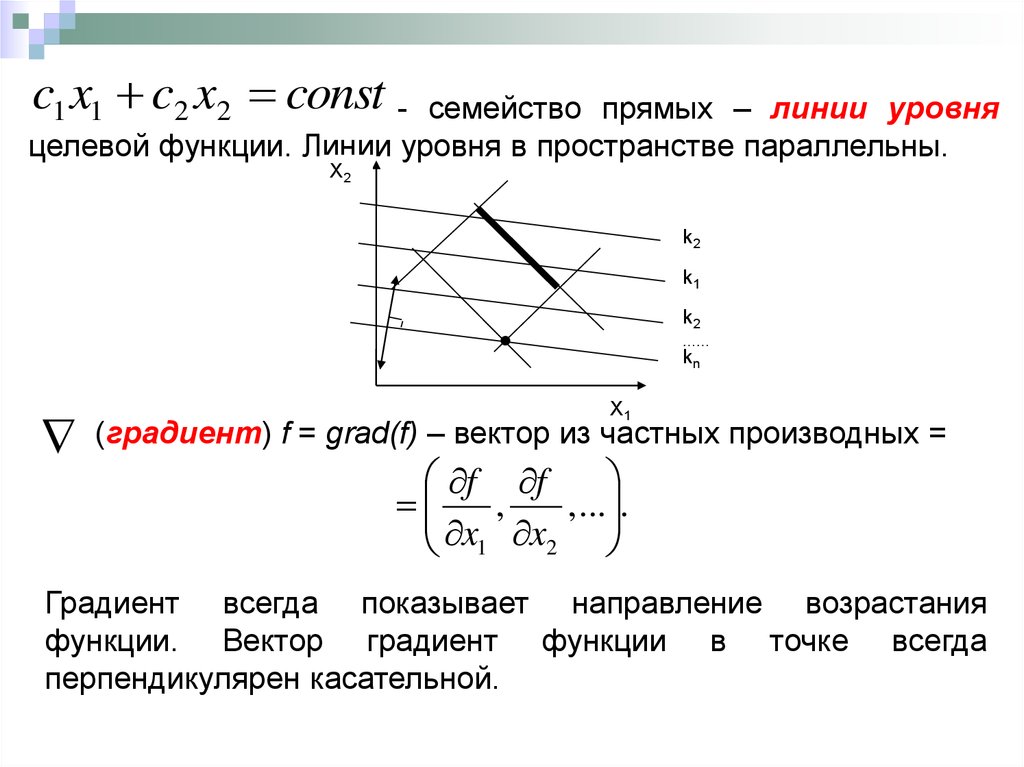
c1 x1 c2 x2 const -
семейство прямых – линии уровня
целевой функции. Линии уровня в пространстве параллельны.
X2
k2
k1
k2
……
kn
X1
(градиент) f = grad(f) – вектор из частных производных =
f f
,
, ... .
x1 x2
Градиент всегда показывает направление возрастания
функции. Вектор градиент функции в точке всегда
перпендикулярен касательной.

12.

Свойства решений ЗЛП
Теорема 1 Т е о р е м а 1. Множество всех планов
задачи линейного программирования выпукло.
(или ОДЗ ЗЛП выпукла)
Доказательство.
Необходимо доказать, что если Х1 и Х2 — планы задачи линейного
программирования, то их выпуклая линейная комбинация
Х = 1Х1 + 2Х2, 1 0, 2 0, 1 + 2 = 1 также план задачи.
Так как Х1 и Х2 — планы задачи, то выполняются соотношения
АХ1 = А0, Х1 0, АХ2 = А0, Х2 0.
Перемножая
АХ = A( 1Х1 + 2Х2) = 1АХ1 + 2АХ2 = 1А0 + 2А0 =
= ( 1 + 2)А0 = А0,
получаем, что Х удовлетворяет системе (2.43).
(2.52)
xi 0 (i = 1, 2, ..., n)
(2.53)
Но так как Х1 0; Х2 0, 1 0, 2 0, то и Х 0, т. е. удовлетворяет
и условию (2.53). Таким образом Х — план задачи линейного
программирования.

13.

Теорема 2 Целевая функция ЗЛП достигает своего
минимального (максимального) значения в угловой точке
многогранника решений. Если целевая функция достигает
своего экстремального значения более чем в одной угловой
точке многогранника решений, то она достигает того же
значения в любой линейной выпуклой комбинации этих
угловых точек.

14.

Доказательство.
Предположим, что многогранник решений ограниченный,
имеющий конечное число угловых точек. Обозначим его через К. В
двумерном пространстве К имеет вид многоугольника,
изображенного на рис. 2.5. Обозначим угловые точки К через Х1,
Х2, ..., Хp, а оптимальный план — через Х0. Тогда Z(X0) Z(X) для
всех Х из К. Если Х0 — угловая точка, то первая часть теоремы
доказана. Предположим, что Х0 не является угловой точкой; тогда
Х0 на основании теоремы 1 можно представить как выпуклую
линейную комбинацию угловых точек К, т. е.
Х0 = 1Х1 + 2Х2 + ... + pХp,
I 0 (i = 1, 2, ..., p), .
y
Так как Z(X) — линейная функция, получаем
Z(X) = Z( 1Х1 + 2Х2 + ... + pХp) =
X2
= 1Z(X1) + 2Z(X2) + ...
X0
… + pZ(Xp).
(2.54)
X
X
3
K
1
X
X
p
р и с .2 .5
i
X

15.

В этом разложении среди значений Z(Xi) (i = 1, 2, ..., p) выберем
наименьшее пусть оно соответствует угловой точке Хk (1 k p) и
обозначим его через m, т. е. Z(Xk) = m. Заменим в (2.54) каждое
значение Z(Xi) этим наименьшим значением. Тогда, так как i 0, , то
Z(X0) 1m + 2m + ... + pm = m.
По предположению, Х0 — оптимальный план, поэтому, с одной стороны,
Z(X0) m, но с другой стороны, доказано, что Z(X0) m, значит,
Z(X0) = m = Z(Xk), где Xk — угловая точка. Итак, существует угловая
точка Xk, в которой линейная функция принимает минимальное
значение.
Для доказательства второй части теоремы допустим, что Z(X) принимает
минимальное значение более чем в одной угловой точке, например в
точках Х1, Х2, ..., Хq, 1< q p; тогда Z(X1) = Z(X2) = ... = Z(Xq) = m. Если
Х — выпуклая линейная комбинация этих угловых точек:
Х = 1Х1 + 2Х2 + ... + qХq , I 0 (i = 1, 2, ..., q), ,
то
Z(X) = Z( 1Х1 + 2Х2 + ... + qХq) = 1Z(X1) + 2Z(X2) + ...
… + qZ(Xq) = 1m + 2m + ... + qm = m.
т. е. линейная функция Z принимает минимальное значение в
произвольной точке Х, являющейся выпуклой линейной комбинацией
угловых точек Х1, Х2, ..., Хq .

16. Графический метод решения задачи линейного программирования

Пусть задача линейного программирования задана в двумерном пространстве, т. е.
ограничения содержат две переменные.
Найти минимальное значение функции
Z = C1x1 + C2x2
при условиях
a11x1 a12 x2 b1,
a21x1 a22 x2 b2 ,
. . . . .
am1x1 am2 x2 bm ,
х1 0, х2 0.

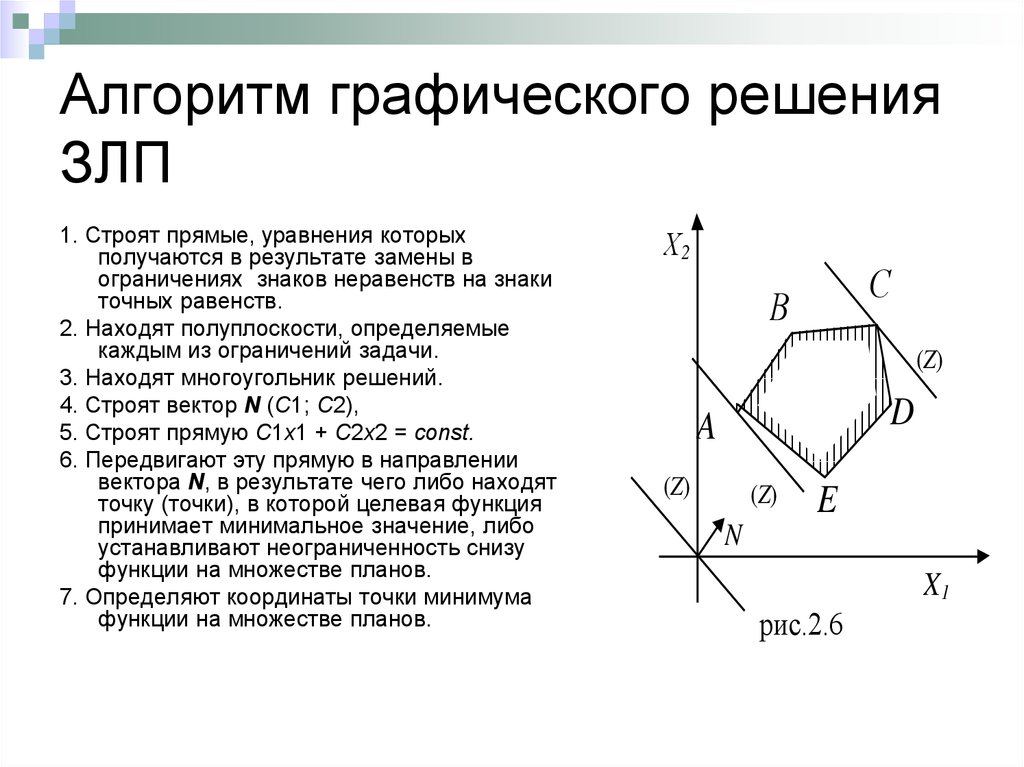
17. Алгоритм графического решения ЗЛП

1. Строят прямые, уравнения которых
получаются в результате замены в
ограничениях знаков неравенств на знаки
точных равенств.
2. Находят полуплоскости, определяемые
каждым из ограничений задачи.
3. Находят многоугольник решений.
4. Строят вектор N (C1; C2),
5. Строят прямую C1х1 + C2x2 = const.
6. Передвигают эту прямую в направлении
вектора N, в результате чего либо находят
точку (точки), в которой целевая функция
принимает минимальное значение, либо
устанавливают неограниченность снизу
функции на множестве планов.
7. Определяют координаты точки минимума
функции на множестве планов.
Х2
С
В
(Z)
D
A
(Z)
(Z)
E
N
X1
рис.2.6

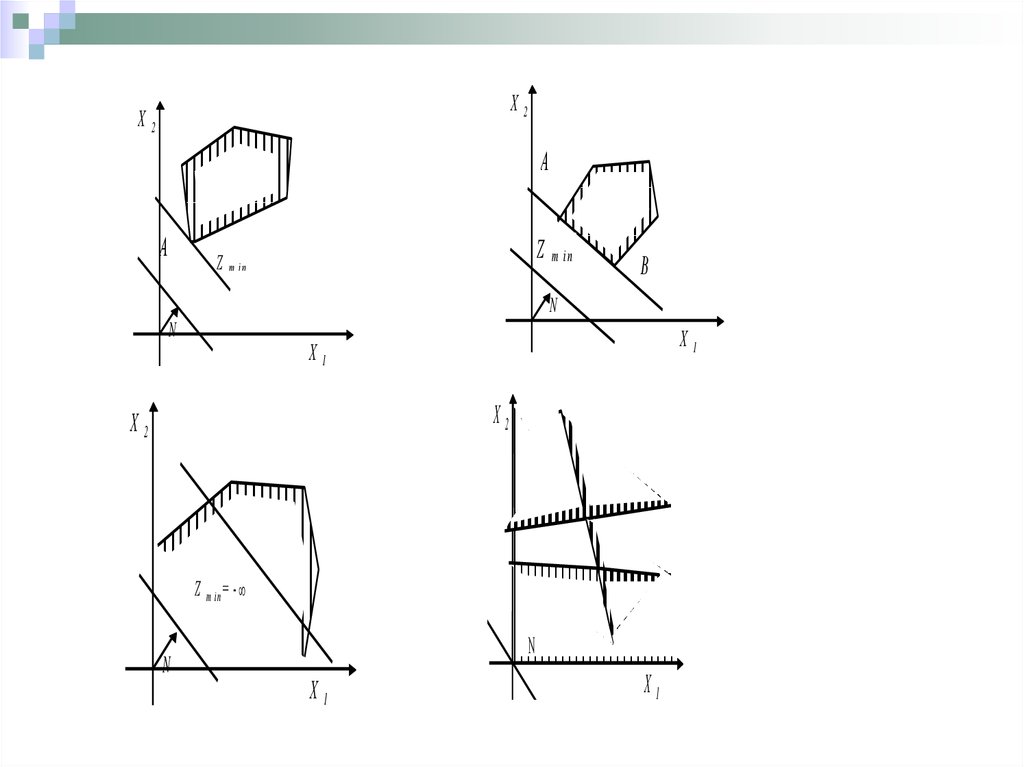
18.

Х2
Х2
A
A
Z
Z
m in
m in
B
N
N
X1
X1
Х2
Х2
Z m in = -
N
N
X1
X1

19. Симплекс-метод

20.

Идея симплекс-метода
Решение основной задачи линейного программирования
геометрическим методом является наглядным в случае двух и даже трех
переменных. Для случая же большего числа переменных этот метод
становится невозможным.
В связи с этими трудностями возникла задача рационального
перебора крайних точек решения основной задачи линейного
программирования.
Общая идея наиболее широко применяемого симплексного
метода состоит в последовательном улучшении плана для решения ЗЛП.
Если известны какая-нибудь крайняя точка и значение целевой
функции, то все крайние точки, в которых целевая функция принимает
худшее значение, заведомо не нужны. Отсюда естественно стремление
найти способ перехода от данной крайней точки к смежной по ребру
лучшей, от нее к еще лучшей (не худшей). Для этого нужно иметь
признак того, что лучших крайних точек, чем данная крайняя точка,
вообще нет.

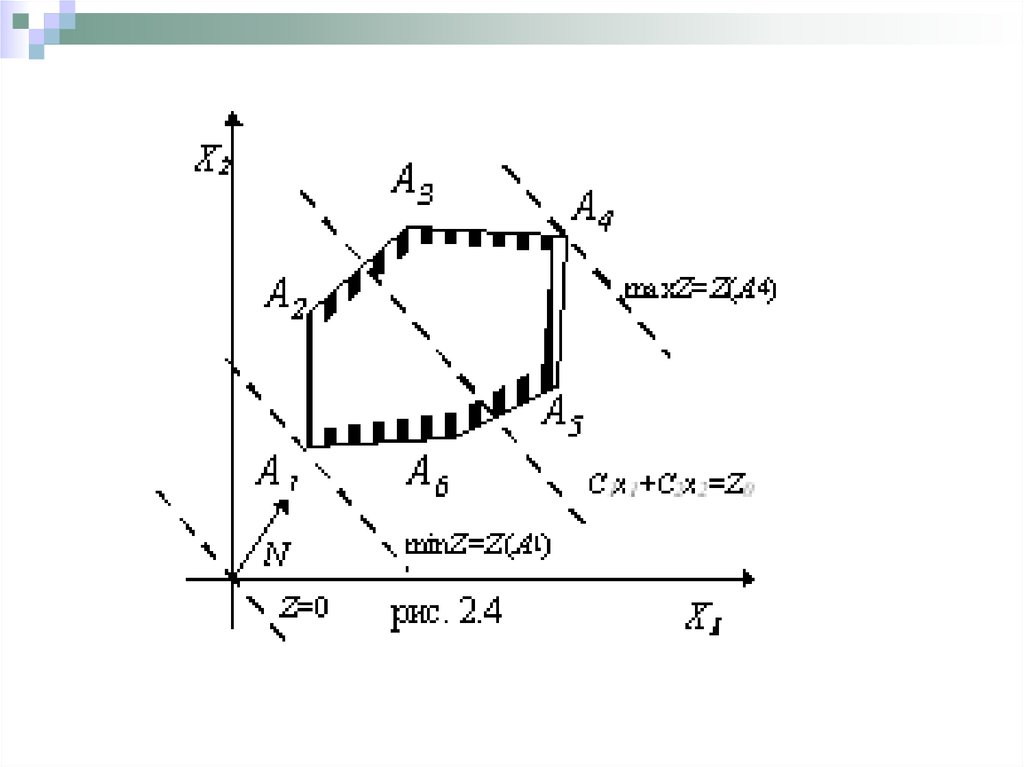
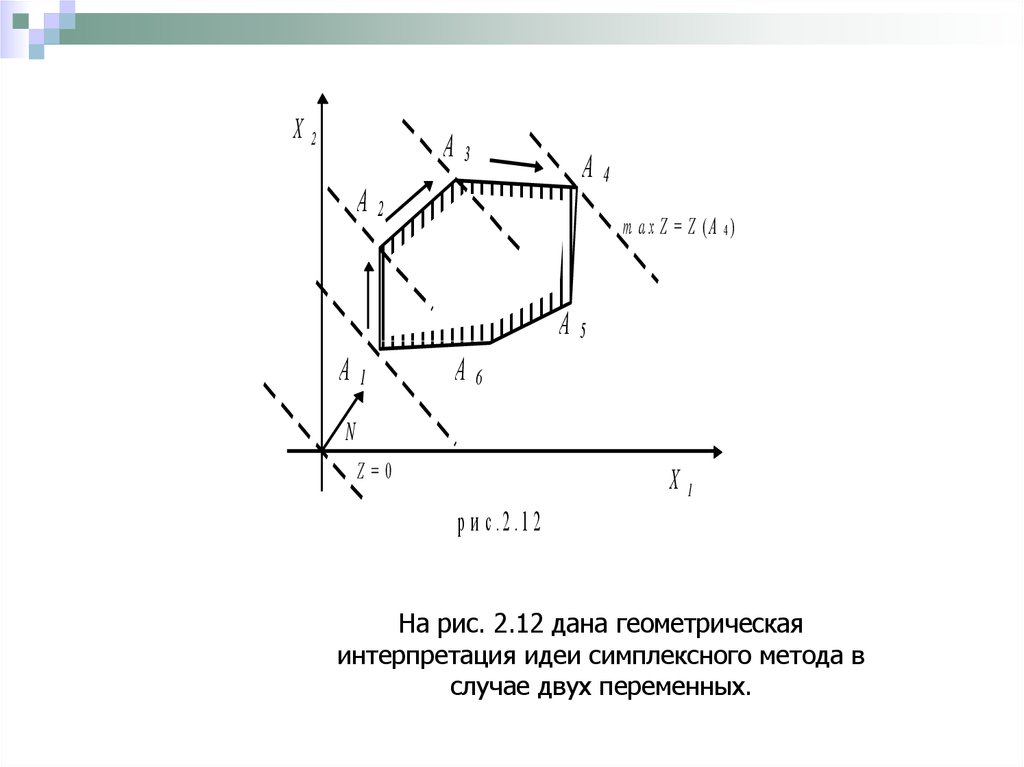
21.

Х
А
2
А
3
А
2
m a x Z = Z (A 4)
А
A
1
4
А
5
6
N
Z=0
X
1
р и с .2 .1 2
На рис. 2.12 дана геометрическая
интерпретация идеи симплексного метода в
случае двух переменных.

22.

Теоретические обоснования симплекс-метода. Любую ЗЛП можно представить в
эквивалентном предпочтительном виде:
max (min) Z
xi
n
c j x j ,
j 1
(2.58)
n
aij x j bi , bi 0 (i 1, m),
j m 1
x j 0 ( j 1, n).
(2.59)
(2.60)
Выразим базисные переменные х1, х2, ..., xm из равенств (2.59) через свободные хm+1, хm+2,
..., xn и подставим их в целевую функцию. После группировки подобных членов получим
Z = (c1b1 + c2b2 + ... + cmbm) – ((c1a1,m+1 + c2a2,m+1 + ...
… + cmam,m+1) – cm+1)xm+1 + ((c1a1,m+2 + c2a2,m+2 + ...
… + cmam,m+2) – cm+2)xm+2 + ... + ((c1a1n + c2a2n + ...
… + cmamn) – cn)xn
(2.61)
Введем обозначения:
0 = c1b1 + c2b2 + ... + cmbm = сбА0,
(2.62)
j = (c1a1j + c2a2j + ... + cmamj) – cj = сбАj – cj,
( j 1, n).
(2.63)

23.

где сб = (c1, c2, ..., cm) — вектор коэффициентов целевой функции при базисных
переменных; А0 = (b1, b2, ..., bm)T — вектор-столбец свободных членов; Аj = (a1j, a2j, ..., amj)T —
вектор-столбец коэффициентов при переменных хj.
С учетом равенств (2.61)—(2.63) задача (2.58)—(2.60) примет вид:
n
max (min) Z = 0 - j x j ;
(2.64)
j m 1
xi
n
aij x j bi (i 1, m),
j m 1
x j 0 ( j 1, n),
(2.65)
(2.66)
( j 1, n).
где 0 = сбА0; j = сбАj – cj
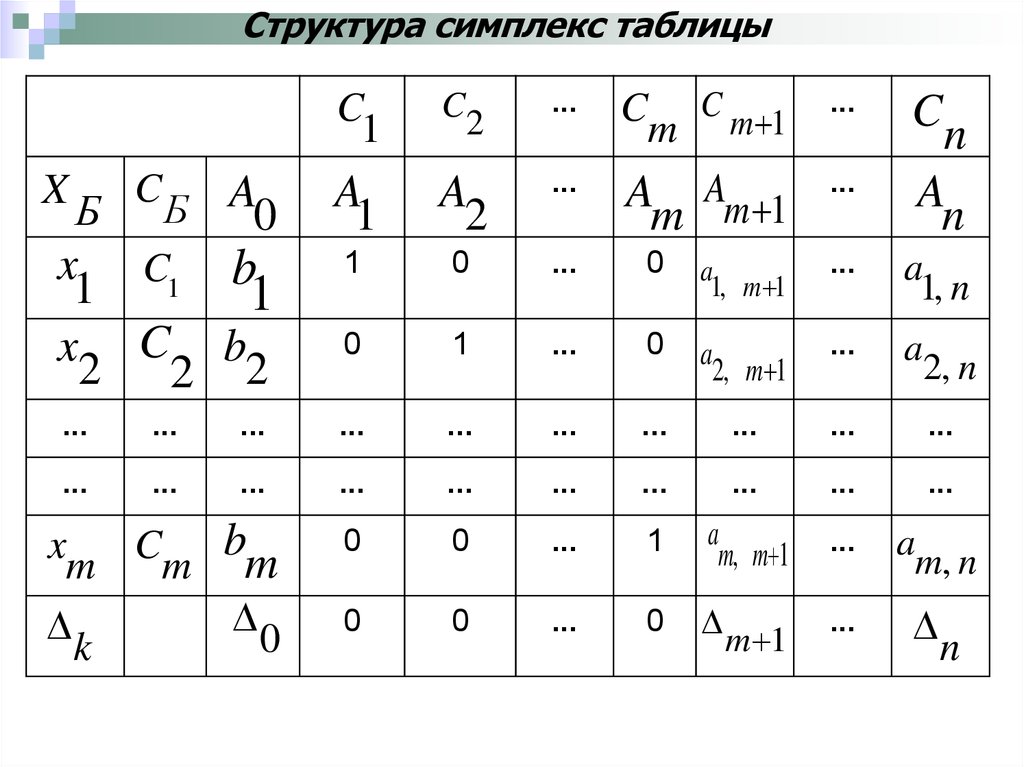
Задачу (2.64)—(2.66) записывают в таблицу, которая называется симплексной (табл.1).
Последнюю строку называют индексной строкой (строкой целевой функции), число 0 = сбА0
— значение целевой функции для начального опорного плана х0, т. е. 0 = Z(х0). Числа
j = сбАjcj (
j 1, n) называются оценками свободных переменных.

24.

Т е о р е м а 1. Пусть исходная задача решается на максимум. Если для некоторого
опорного плана все оценки j
( j 1, n) неотрицательны, то такой план оптимален.
n
Доказательство. Так как Z = 0 —
j x j и по условию j 0
j m 1
( j 1, n) , то Z
n
достигает максимального значения при
j x j = 0. Это возможно лишь при xm+1 = 0,
j m 1
xm+2 = 0, ..., xn =0, т. е. опорный план (b1, b2, ..., bm, 0m + 1, 0m + 2, …, 0m + n) оптимален.
Т е о р е м а 2. Если исходная задача решается на минимум и для некоторого опорного
плана все оценки j ( j 1, n) неположительны, то такой план оптимален.
Доказательство аналогично предыдущему случаю.
Переход к нехудшему опорному плану.
Т е о р е м а 3. Если k < 0 для некоторого j = k и среди чисел aik ( i 1, m )нет
положительных, то целевая функция ЗЛП не ограничена на множестве ее планов.
Т е о р е м а 4. Если опорный план Х ЗЛП не вырожден и k < 0, но среди чисел aik есть
положительные (не все aik < 0), то существует опорный план X’ такой, что Z(X’) > Z(X).

25.

Теорема 1 Пусть исходная задача решается на минимум, тогда
если для некоторого опорного решения все z-оценки
j
неположительные,
оптимальным.
то
( j 1, n)
такое
опорное
решение
является
Теорема 2 Если исходная задача решается на максимум, то в
случае, когда все j ( j 1, n) – неотрицательные, получаем
оптимальное решение исходной задачи.

26.

Теорема 3 Если опорный план ЗЛП не вырожден и k 0
такое, что в k-ом столбце системы ограничений есть хотя бы
одно положительное число, т.е. не все , то существуе
такое опорное решение x ', что z ( x ' ) z ( x ), где x – исходное
опорное.
aik 0
Теорема 4 Если опорное решение ЗЛП не вырождено и k 0
и в k-ом столбце системы ограничений нет ни одного
положительного числа, т.е. все a ik 0
функция
не ограничена на ОДР.
, то целевая

27.

Структура симплекс таблицы
...
C
m 1
...
A
2
...
A Am 1
m
...
1
0
...
0
a
1, m 1
...
a
1, n
0
1
...
0
a
2, m 1
...
a
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
0
0
...
1
a
m, m 1
...
a
m, n
0
0
...
0
...
C
1
C
A
1
x C1 b
1
1
x C b
2 2 2
...
...
...
...
X
Б
C
Б A0
x
C bm
m
m
0
k
2
m
C
m 1
C
n
A
n
2, n
n

28.

Методы контроля:
1. Z-оценки при базисных переменных равны нулю 0 i (1,m);
i
2. Значения правой части всегда неотрицательны b 0
j
j (1,n);
3. Значение целевой функции на каждом шаге не ухудшается.
Зацикливание
Зацикливание может возникать при наличии вырожденного
опорного решения. Выражается в том, что значение целевой
функции на следующем шаге не меняется.