Похожие презентации:
Математическая модель задач линейного программирования и их геометрическая интерпретация. Лекция 3
1.
ЛЕКЦИЯ 3.Математическая модель задач
линейного программирования и их
геометрическая интерпретация
2.
Вопрос 1.Математическая модель основной
задачи линейного программирования
3.
.Линейное программирование – это раздел высшей математики,
занимающийся разработкой методов отыскания экстремальных
значений линейной функции, на неизвестные которой наложены
линейные ограничения. Задачи линейного программирования
относятся к задачам на условный экстремум функции.
Рассмотрим задачу линейного программирования с ограничениямиравенствами, так называемую каноническую (основную) ЗЛП, которая
ставится следующим образом.
1) Имеется набор переменных {xi}, где
i 1, n
4.
2) 3адана система m линейно независимых уравнений, называемаясистемой ограничений:
a 11 x 1 a 12 x 2 a 1 n x n b 1
a 21 x 1 a 22 x 2 a 2 n x n b 2
a m1 x 1 a m 2 x 2 a m n x n b m
5.
3) Задана целевая функция (ЦФ):n
L x c1 x 1 c 2 x 2 c n x n c i x i
i 1
4) Требуется найти неотрицательные значения переменных (хi 0),
которые удовлетворяют системе ограничений и обращают в минимум
ЦФ.
Допустимым решением ЗЛП называется любая совокупность
переменных {xj}, удовлетворяющая ограничениям.
Оптимальным решением называется то из допустимых, при котором
ЦФ обращается в минимум.
6.
Напомню проблемы существования допустимых решений, изучаемые вАналитической геометрии.
Матрицей системы линейных уравнений называется таблица,
составленная из коэффициентов при переменных:
a 11 a 1 n
a m1 a m n
Расширенной матрицей называется матрица, дополненная столбцом
свободных членов:
a 11 a 1 n b1
a m1 a m n b m
7.
Рангом матрицы называется наибольший порядок отличного от 0определителя, который можно получить, вычеркивая из матрицы
какие-то строки или столбцы.
В линейной алгебре доказывается (теорема Кронекера-Капелли),
что для совместности системы линейных уравнений необходимо и
достаточно, чтобы ранг матрицы системы был равен рангу ее
расширенной матрицы.
Будем называть его рангом системы r. Он представляет собой не
что иное, как число линейно независимых уравнений среди
наложенных ограничений.
Очевидно, что r m и r n.
8.
Возможны 2 случая.1 случай. r = n (т.е. m = n) и уравнения линейно независимы. В этом
случае система уравнений имеет единственное решение. Определитель
системы не равен нулю и решения можно найти с помощью формул
Крамера:
x i
xi
,
где – определитель системы;
x i – определитель, полученный из путем замены i-го столбца
столбцом свободных членов.
Если все xi 0, то найденное решение является допустимым. Оно же
является и оптимальным.
Этот тривиальный случай в линейном программировании мы
рассматривать не будем.
9.
2 случай. r < n – число независимых уравнений, которым должныудовлетворять переменные, меньше числа самих переменных.
Тогда, если система совместна, у нее существует бесчисленное
множество решений.
При этом n-r переменным мы можем придавать произвольные
значения (это свободные переменные), а остальные r переменных
выразятся через них (это базисные переменные).
Поскольку число уравнений m меньше числа переменных n, то одно
из возможных решений можно найти, если n-m переменных положить
равными нулю.
Полученную систему m уравнений с m неизвестными можно решить
обычными методами линейной алгебры.
10.
Необходимым и достаточным условием существования решенияявляется неравенство нулю определителя системы , составленного из
коэффициентов при неизвестных.
Если это условие не выполняется, то можно приравнять 0 другие n-m
переменных.
Полученное решение называется опорным.
Базисом называется любой набор m переменных, у которых 0.
Вывод: суть ЗЛП состоит в следующем: из множества допустимых
решений найти оптимальное, которое обеспечивает min (max)
линейной целевой функции.
11.
Вопрос 2.Геометрическая интерпретация
задачи линейного
программирования
12.
Для более полного представления сути ЗЛПгеометрическую интерпретацию на конкретном примере.
Задана система уравнений-ограничений:
дадим
ее
2 x 1 x 2 x 3 2
x1 2 x 2 x 4 2
x x x 5
1
2
5
и целевая функция:
L x 2 x1
Требуется
найти
неотрицательные
значения
переменных,
удовлетворяющих условиям и обращающих в минимум ЦФ.
13.
Для удобства задачу минимизации ЦФ преобразуем в задачумаксимизации,
что
легко
сделать,
проведя
элементарные
преобразования (рис. 1):
L L x 1 x 2
|
Рис 1. Пример преобразования задачи
минимизации ЦФ в задачу максимизации.
14.
В данном примере число уравнений m = 3, число переменных n = 5.Следовательно, имеем m = 3 базисных переменных и n–m=2 свободных
переменных.
Когда
свободных
переменных
две
есть
возможность
проиллюстрировать решение задачи на координатной плоскости.
Выберем в качестве свободных переменные х1 и х2.
По осям Ох1 и Ох2 будем откладывать значения свободных
переменных.
Так как их значения должны быть неотрицательными, то будем
использовать только первую четверть координатной плоскости.
Оставшиеся три переменные – базисные. Разрешим систему
относительно базисных переменных:
x 3 2 2 x 1 x 2
x 4 2 x 1 2 x 2
x 5 x x
1
2
5
15.
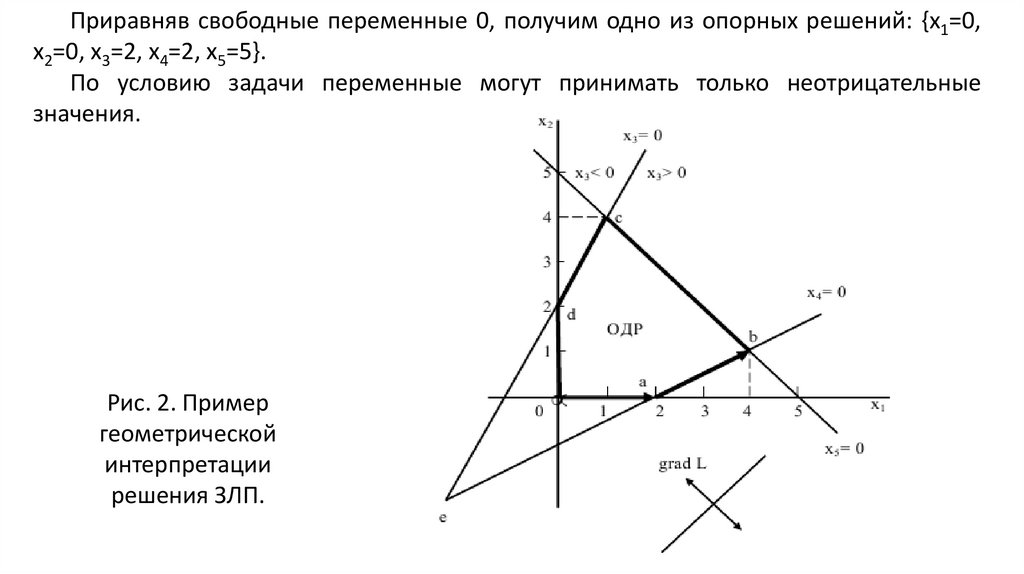
Приравняв свободные переменные 0, получим одно из опорных решений: {x1=0,x2=0, x3=2, x4=2, x5=5}.
По условию задачи переменные могут принимать только неотрицательные
значения.
Рис. 2. Пример
геометрической
интерпретации
решения ЗЛП.
16.
Примем в первом уравнении x3=0 (ее крайнему значению). Построимпрямую 2 2 x 1 x 2 0 (рисунок 2).
Определим для x3 положительную полуплоскость. Если x1 = x2 = 0, то
x3 = 2.
Значит точка (0; 0) находится в положительной полуплоскости.
Примем во втором уравнении x4=0. Построим прямую 2 x 1 2 x 2 0.
Определим для x4 положительную полуплоскость. Если x1 = x2 = 0, то x4 =
2. Значит точка (0; 0) находится в положительной полуплоскости.
Примем в третьем уравнении x5=0. Построим прямую 5 x 1 x 2 0.
Определим для x5 положительную полуплоскость. Если x1 = x2 = 0, то x5 =
5.
Значит точка (0; 0) находится в положительной полуплоскости.
17.
Многоугольник OABCD представляет собой область допустимыхрешений (ОДР). Все точки, принадлежащие ОДР удовлетворяют
системе ограничений.
Отметим два важные момента:
1) ОДР – представляет собой выпуклый многоугольник.
Как известно, выпуклой фигурой называется фигура, обладающая
следующим свойством:
если две точки А и В принадлежат этой фигуре, то и весь отрезок АВ
также принадлежит ей.
2) Так как каждая прямая соответствует обращению в нуль одной из
переменных, то в точках пересечения двух прямых в нуль будут
обращаться две переменные.
18.
Вывод: допустимыми опорными решениями при n–m=2 свободныхпеременных, обращенных в нуль, являются вершины многоугольника
ОДР.
Из опорных решений надо выбрать оптимальное, обращающее в
максимум ЦФ.
|
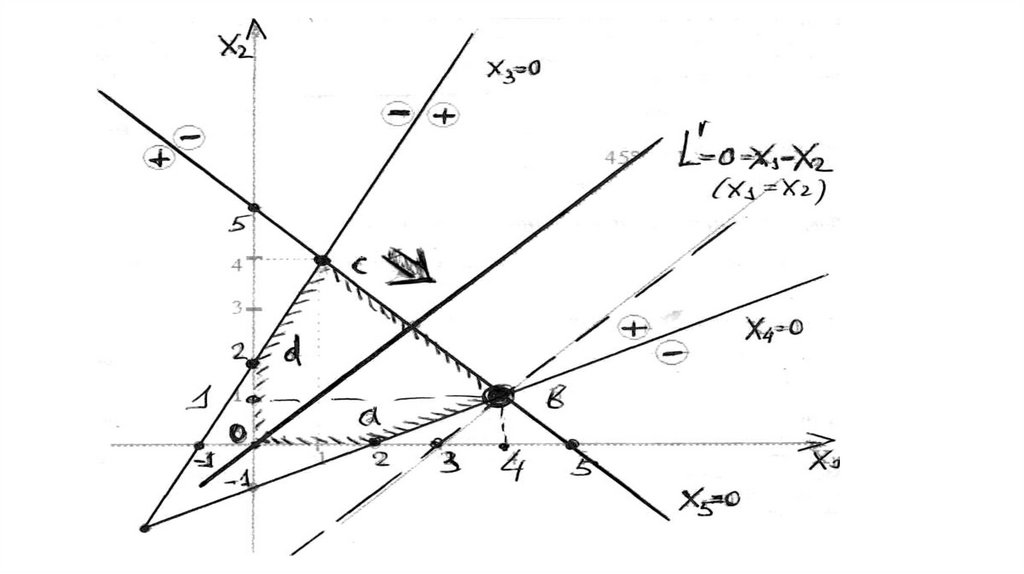
L
Положим 0 и построим прямую x 1 x 2 0 .
Отметим стрелкой направление возрастания ЦФ (направление вправо вниз).
Будем двигать прямую ЦФ параллельно себе в направлении ее
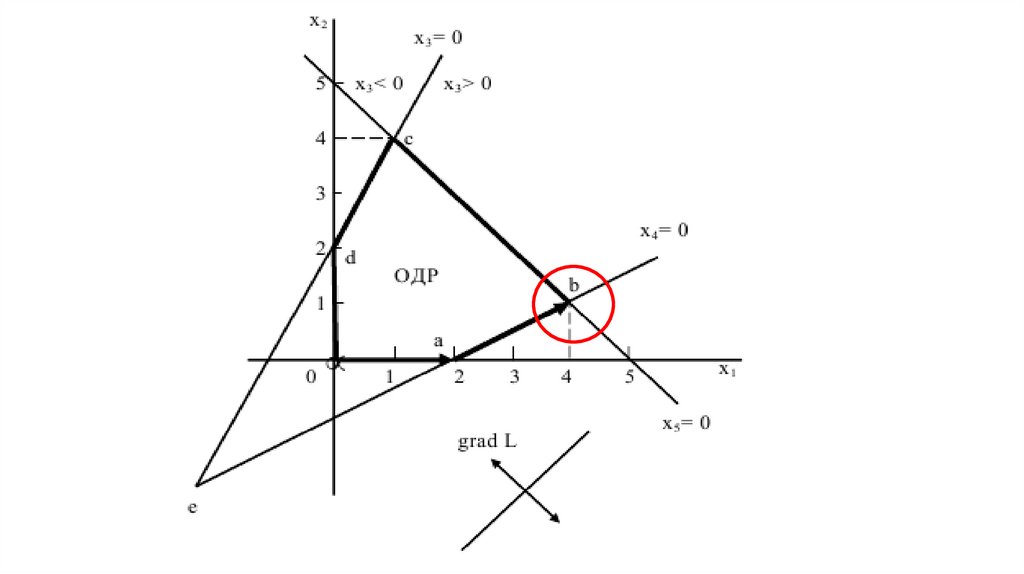
возрастания. В точке b она выйдет из ОДР.
Значит, именно в точке b является оптимальное решение, при
котором ЦФ принимает максимальное значение. В этой точке
свободные переменные принимают оптимальные значения. Подставив
эти значения, можно найти оптимальные значения базисных
переменных, а также оптимальное (максимальное) значение ЦФ.
19.
Определить координаты т. b можно двумя способами:1) графически по чертежу;
2) аналитически, решив совместно уравнения (т. В лежит на
пересечении этих прямых):
2 x 1 2 x 2 0
5 x 1 x 2 0
В результате получим решение {4; 1; 9; 0; 0}, при котором ЦФ L = –3.
Таким образом, если число независимых уравнений-ограничений m
на 2 меньше, чем число переменных n, (т.е. в ЗЛП фигурируют 2
свободные переменные и любое число базисных), то решение ЗЛП
может быть получено простым геометрическим построением.
20.
21.
22.
Отметим полученные закономерности.1. Оптимальное решение ЗЛП, если оно существует лежит на границе
ОДР в одной из ее вершин, где по крайней мере n–m переменных
обращаются в нуль.
Эти переменные называются свободными, а каждое из решений,
находящихся в вершине ОДР – опорным.
2. Для нахождения оптимального решения необходимо перебрать
все опорные и выбрать то из них, которое обеспечивает экстремум ЦФ.
В случае, когда n–m=3, геометрическую интерпретацию следует
давать в пространстве 3-х координат.
В этом случае ОДР будет представлять собой выпуклый многогранник.
23.
Задача на следующую неделю (время лабораторных работ№ 1 и № 2):
По лабораторной работе № 1:
по вариантам решить 2 задачи ЛП с помощью электронных
таблиц MS Excel.
Задание будет выдано в СЭО Moodle.




















 Математика
Математика








