Эконометрика. Нормальное распределение

1.

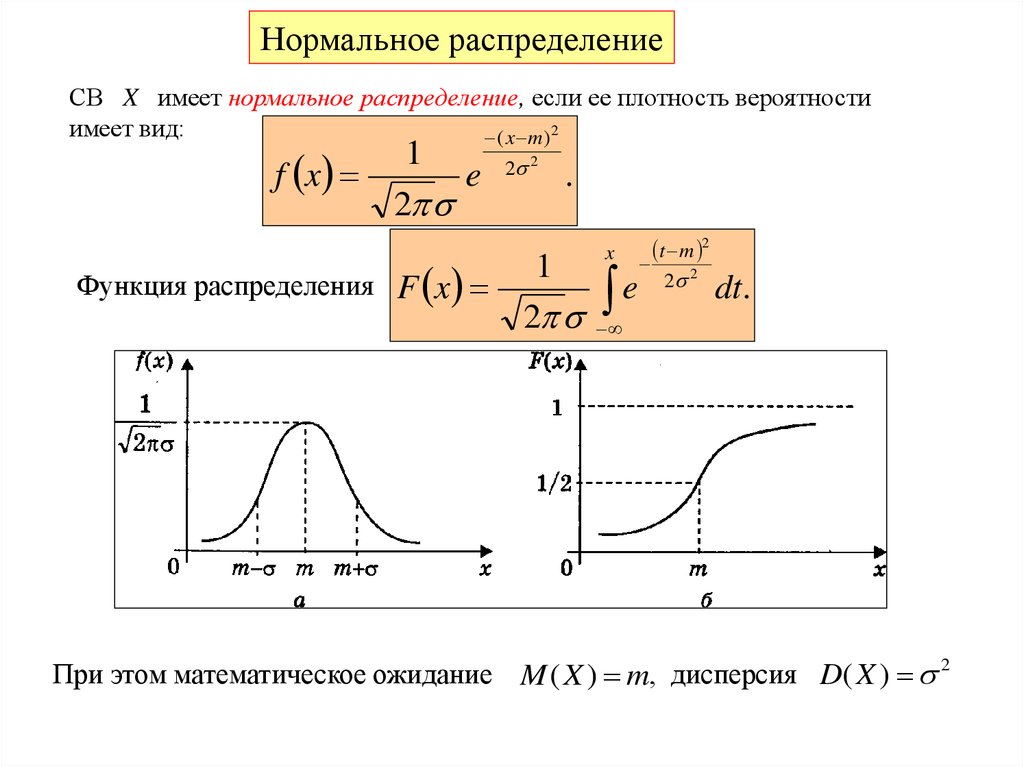
Нормальное распределение
СВ X имеет нормальное распределение, если ее плотность вероятности
имеет вид:
( x m )2
f x
1
e
2
Функция распределения F x
2 2
.
1
2
x
e
t m 2
2 2
dt.
При этом математическое ожидание M ( X ) m, дисперсия D( X ) 2

2.

Если СВ X имеет нормальное распределение с параметрами
математического ожидания M ( X ) m и дисперсией D( X ) 2
то X ~ N m, 2
СВ X
N (0,1) называется стандартизированной
СВ X
N (0,1) обозначим через U , т.е. U
f u
1
e
2
u2
2
F u
;
Если СВ X ~ N m, 2 то U
Функция Лапласа: u
1
2
u
X m
e
t2
2
1
2
N (0,1)
u
e
t2
2
dt.
N (0,1)
dt F u 0,5.
0
Вероятность того, что CВ X ~ N m, 2 будет принимать значения между a и b
исчисляется
b m
a m
b m
a m
P a X b F
F
.

3.

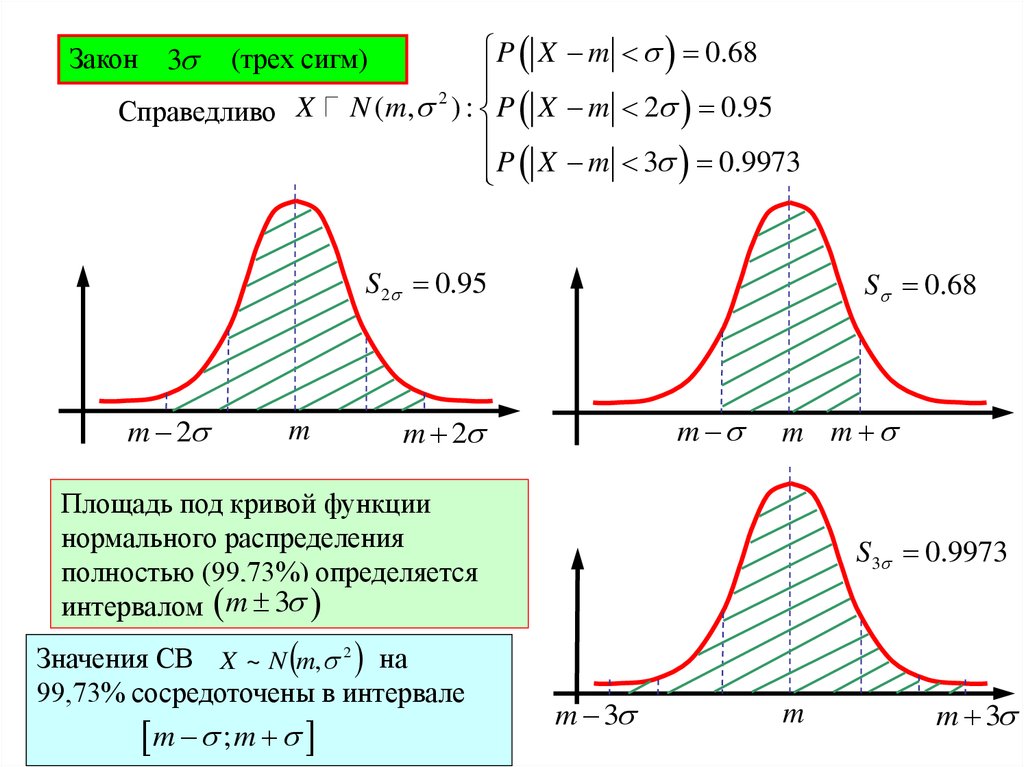
Закон
3
P X m 0.68
2
N ( m, ) : P X m 2 0.95
P X m 3 0.9973
(трех сигм)
Справедливо X
S2 0.95
m 2
m
S 0.68
m
m 2
m m
Площадь под кривой функции
нормального распределения
полностью (99,73%) определяется
интервалом m 3
Значения СВ X ~ N m, 2 на
99,73% сосредоточены в интервале
m ; m
S3 0.9973
m 3
m
m 3

4.

Линейная комбинация нормальных СВ имеет нормальное распределение
X
Y
N (mx , x2 )
Z aX bY
2
N (my , y )
mz amx bm y
N (mz , ) 2
2 2
2 2
a
b
y
z
x
2
z
Многие экономические показатели имеют нормальный или близкий к
нормальному закон распределения. Например, доход населения, прибыль
фирм в отрасли, объем потребления и т.д. имеют близкое к нормальному
распределение.
Нормальное распределение используется при проверке различных гипотез в
статистике (о величине математического ожидания при известной дисперсии,
о равенстве математических ожиданий и т.д.).
При моделировании экономических процессов приходится рассматривать СВ,
которые представляют собой алгебраическую комбинацию нескольких СВ.
При этом желательно иметь возможность прогнозирования поведения таких
СВ.

5.

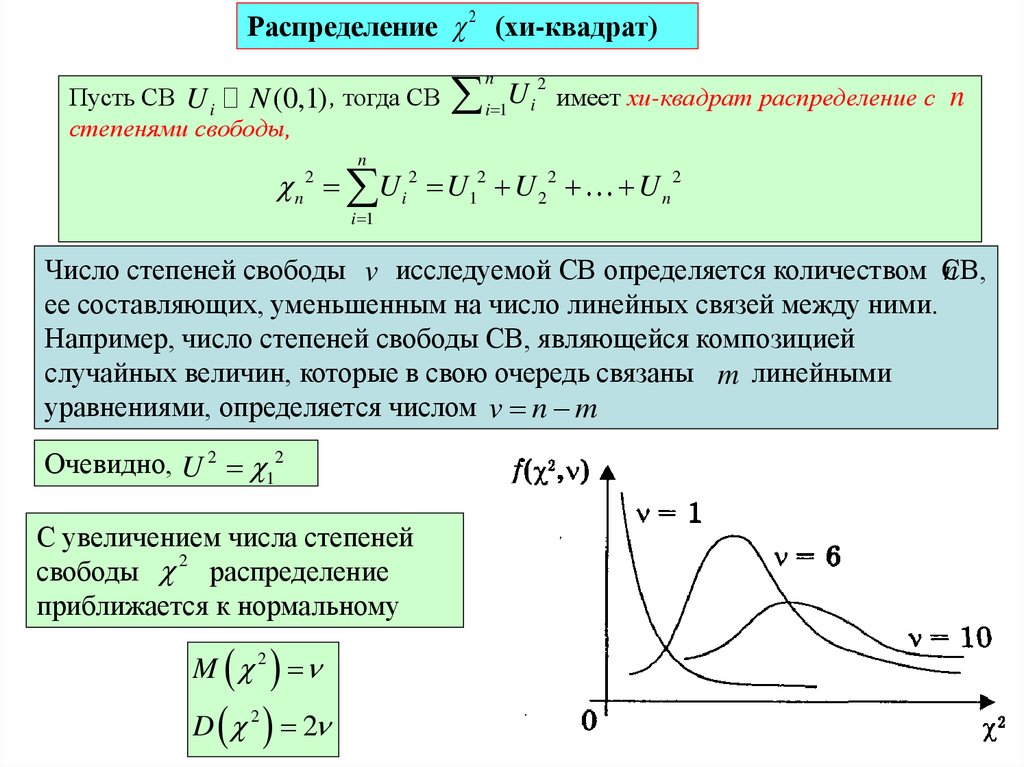
Распределение 2 (хи-квадрат)
Пусть СВ U i N (0,1) , тогда СВ
степенями свободы,
n
n
2
U
имеет хи-квадрат распределение с n
i
i 1
n U i 2 U12 U 2 2
2
i 1
U n2
Число степеней свободы v исследуемой СВ определяется количеством СВ,
n
ее составляющих, уменьшенным на число линейных связей между ними.
Например, число степеней свободы СВ, являющейся композицией
случайных величин, которые в свою очередь связаны m линейными
уравнениями, определяется числом v n m
Очевидно, U 2 12
С увеличением числа степеней
свободы 2 распределение
приближается к нормальному
M 2
D 2 2

6.

X
n
Y
m
2
2
Z X Y
n2 m
Если СВ X n 2 и Y m 2 имеют
распределение хи-квадрат с n и
степенями свободы, то их сумма также
имеет распределение хи-квадрат с
степенями свободы
Распределение хи-квадрат применяется для нахождения интервальных
оценок и проверки статистических гипотез