Типичные законы распределения вероятностей. Нормальное распределение. Показательное распределение. Равномерное распределение

1. Типичные законы распределения вероятностей. Нормальное распределение Показательное распределение. Равномерное распределение. Их

КАЛАБУХОВА Галина Валентиновна
К.социол.н., доцент

2. Вопросы темы

Типичные законы распределения вероятностей.
Нормальное распределение. Числовые характеристики
Показательное распределение. Числовые характеристики.
Равномерное распределение. Числовые характеристики.
Функция надежности.
Показательный закон надежности

3. Определения

Случайная величина называется дискретной, если
ее различные возможные значения можно
перенумеровать. Множество возможных значений
может быть конечным или бесконечным (ряд
натуральных чисел).
Непрерывная случайная величина в результате
испытания может принимать любое значение из
некоторого промежутка – конечного или
бесконечного.

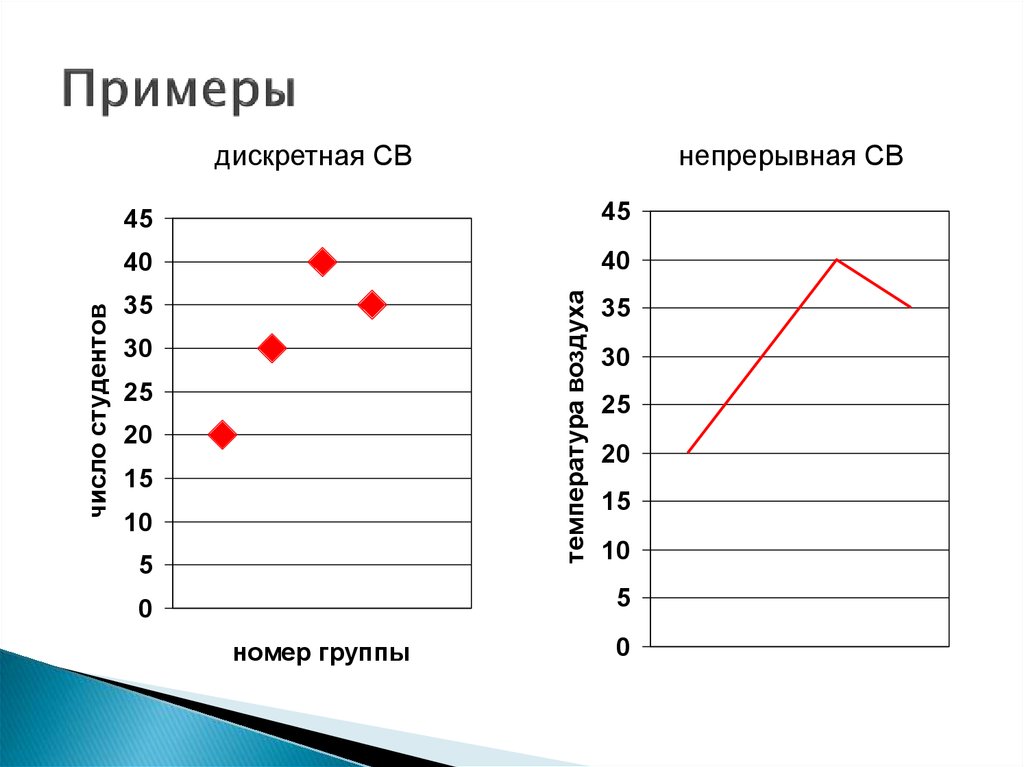
4. Примеры

непрерывная СВ
45
45
40
40
температура воздуха
число студентов
дискретная СВ
35
30
25
20
15
10
5
35
30
25
20
15
10
5
0
номер группы
0

5. Характеристики ДСВ

Законом распределения дискретной случайной
величины X называется соответствие между
каждым ее возможным значением x1 и
вероятностью ее появления p1
Функцией распределения вероятностей
дискретной случайной величины X называется
функция F(X), определяющая для каждого
значения x вероятность того, что случайная
величина X примет значение, меньшее x:
F(x)=P(X<x).

6. Характеристики НСВ

Законом распределения непрерывной случайной
величины X называется соответствие между
каждым ее возможным значением x1 и
вероятностью ее появления p1

7. Характеристики НСВ

Функцией распределения вероятностей
непрерывной случайной величины X называется
функция F(X), равная при каждом xЄR
вероятности того, что X в результате испытания
примет значение, меньшее x:
F(x)=P(X<x), xЄR.
Плотностью распределения вероятностей
непрерывной случайной величины X называется
функция f(X), задаваемая равенством:
f(x)=F'(x), xЄR.

8. Числовые характеристики ДСВ

Математическое ожидание дискретной
случайной величины X, заданной таблицей,
X
x1 x2 x3 x4 … xn
P
p1 p2 p3 p 4 … p n
называется число M(X), вычисленное по формуле
n
M ( X ) x1 p1 x2 p2 ... xn pn xi pi
i 1

9. Числовые характеристики ДСВ

Дисперсией дискретной случайной величины X
X
x1 x2 x3 x4 … xn
P
p1 p2 p3 p4 … pn
D(X) называется математическое ожидание
квадрата отклонения случайной величины X от ее
математического ожидания
n
D( X ) M ( X M ( X )) xi2 pi ( M ( X )) 2
2
i 1

10. Числовые характеристики ДСВ

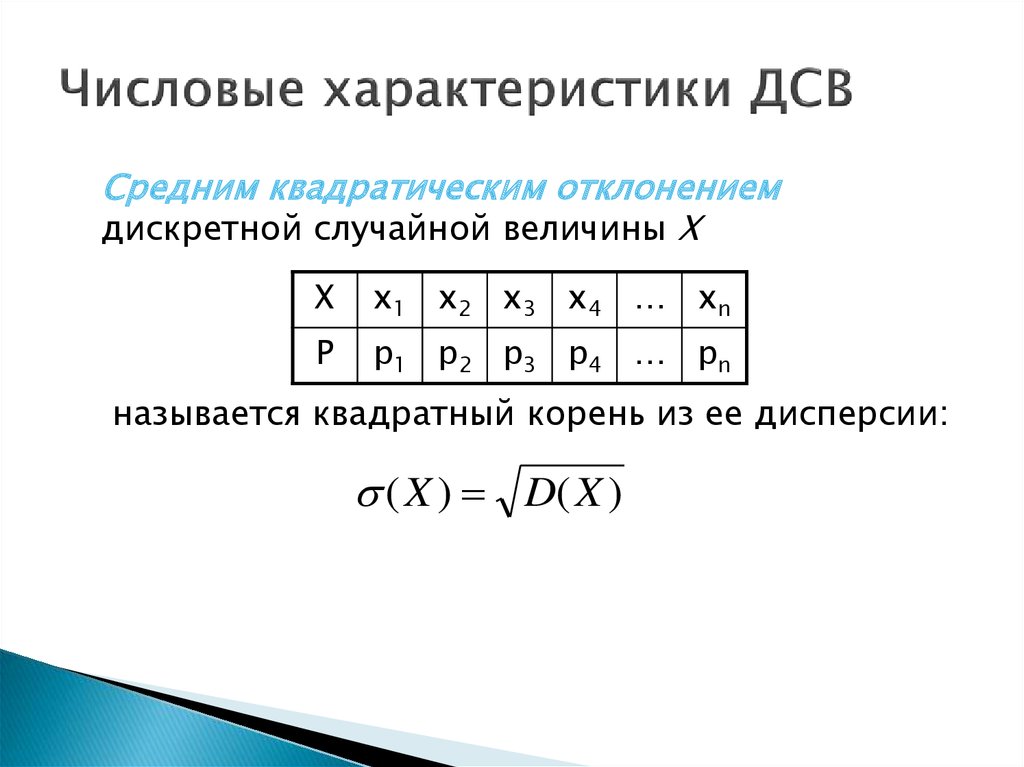
Средним квадратическим отклонением
дискретной случайной величины X
X
x1 x2 x 3 x 4 … xn
P
p1 p 2 p3 p4 … pn
называется квадратный корень из ее дисперсии:
( X ) D( X )

11. Числовые характеристики НСВ

Математическое ожидание непрерывной
случайной величины M(X) удовлетворяет
равенству:
M(X )
xf ( x)dx
Дисперсия непрерывной случайной величины
D(X) определяется формулой:
D( X ) M ( X M ( X )) 2 ( x M ( X )) 2 f ( x )dx

12. Числовые характеристики НСВ

Среднее квадратическое отклонение
непрерывной случайной величины X -
неотрицательный квадратный корень из ее
дисперсии:
( X ) D( X )

13.

14. Виды законов распределения

Нормальное распределение
Показательное (экспоненциальное)
распределение
Равномерное распределение
Распределение Пирсона (χ2 – хи-квадрат)
Распределение Стьюдента
Распределение Фишера

15.

Нормальное распределение
Числовые характеристики

16.

Нормальным называется распределение
вероятностей таких непрерывных случайных
величин, у которых плотность распределения
вероятностей задается формулой:
f ( x)
1
e
2
( x m)2
2 2
,
где m, σ – некоторые числа и σ>0.

17.

Функция распределения вероятностей
вычисляется по формуле:
F ( x ) Ф(
где Ф( x )
1
2
x
e
0
t2
2
dt
x m
)
1
2
- функция Лапласа

18. Функция распределения

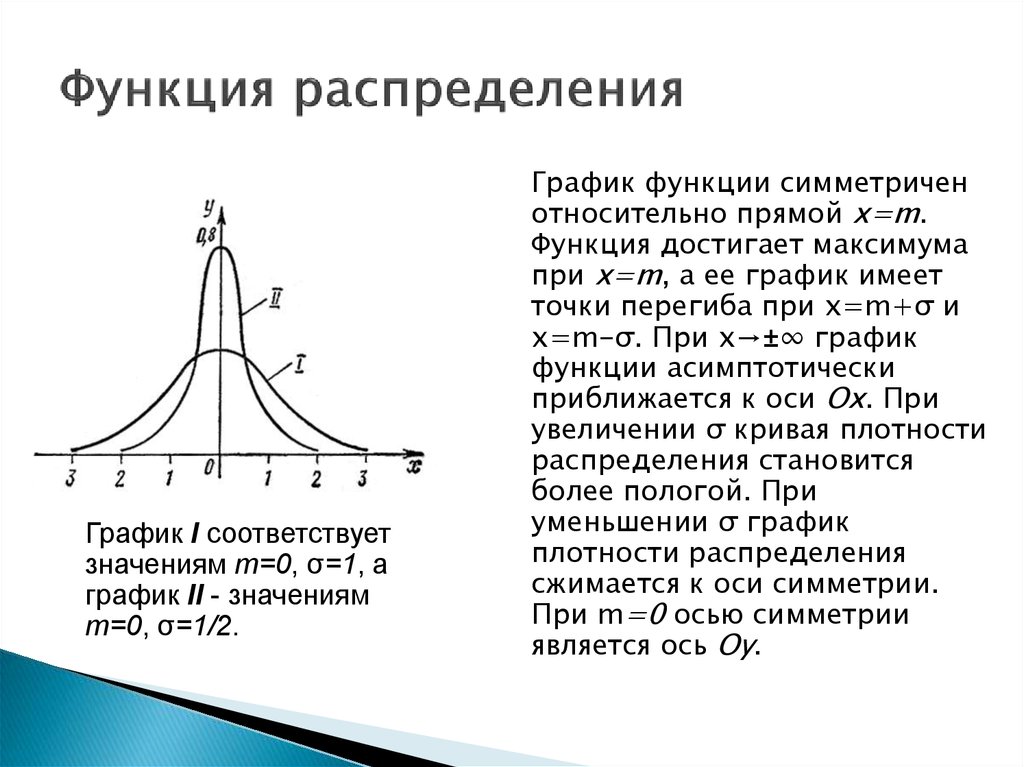
График I соответствует
значениям m=0, σ=1, а
график II - значениям
m=0, σ=1/2.
График функции симметричен
относительно прямой x=m.
Функция достигает максимума
при x=m, а ее график имеет
точки перегиба при x=m+σ и
x=m-σ. При x→±∞ график
функции асимптотически
приближается к оси Ox. При
увеличении σ кривая плотности
распределения становится
более пологой. При
уменьшении σ график
плотности распределения
сжимается к оси симметрии.
При m=0 осью симметрии
является ось Oy.

19. Плотность распределения

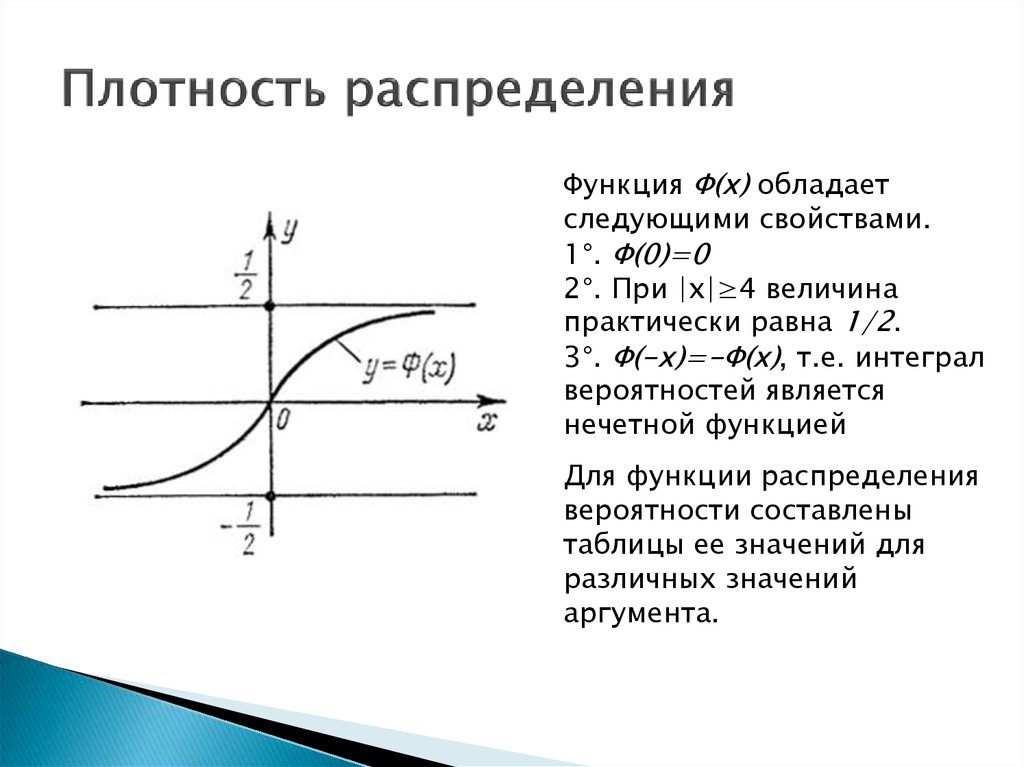
Функция Ф(х) обладает
следующими свойствами.
1°. Ф(0)=0
2°. При |x|≥4 величина
практически равна 1/2.
3°. Ф(-x)=-Ф(х), т.е. интеграл
вероятностей является
нечетной функцией
Для функции распределения
вероятности составлены
таблицы ее значений для
различных значений
аргумента.

20. Числовые характеристики

Математическое ожидание:
M (X )
2
z
(
z
m
)
e
1
/2
dz
2
z
ze
2
m
/2
dz
2
Дисперсия
1
D( X )
2
2
2 ( x m )
(
x
m
)
e
2
/ 2 2
dx 2
Среднее квадратическое отклонение
σ(X)= σ.
z / 2
e
dz m
2

21.

22. Определение

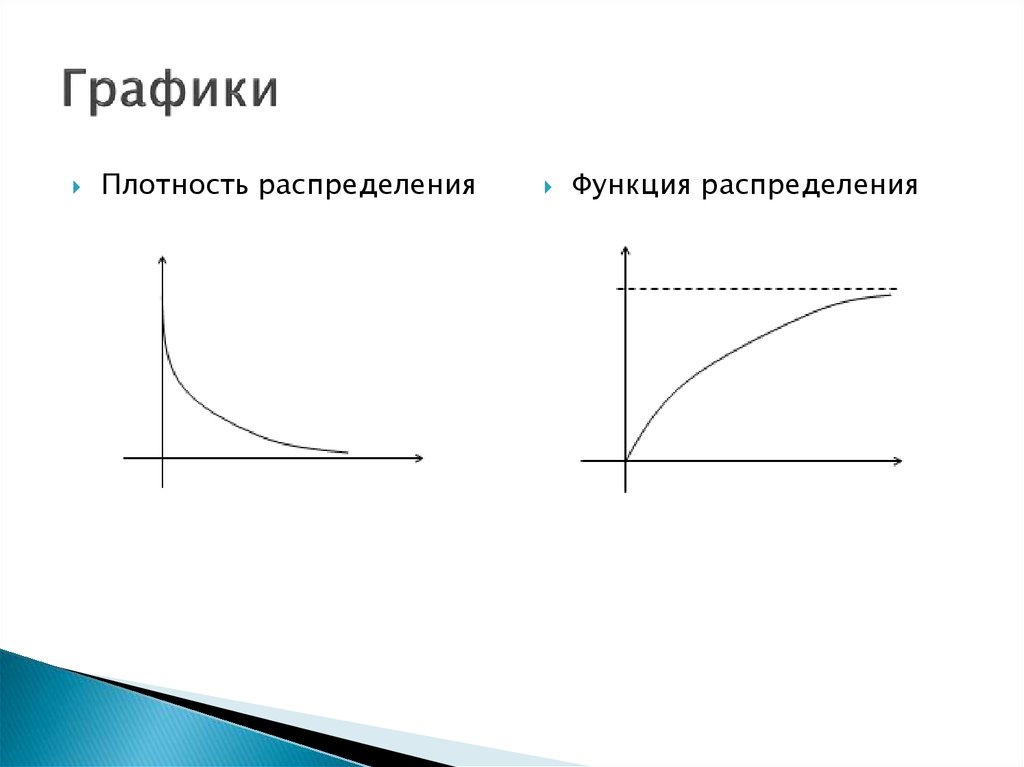
Непрерывная случайная величина X называется
экспоненциально (показательно)
распределенной, если ее плотность
распределения равна:
при x 0
0,
f ( x ) x
e , при x 0
λ – положительный параметр.
Интегральная функция F(X) имеет вид:
при x 0
0,
F ( x)
x
1 e , при x 0

23. Графики

Плотность распределения
Функция распределения

24. Числовые характеристики

Математическое ожидание:
0
0
M ( X ) xf ( x )dx xe x dx
Дисперсия
1
D( X ) x f ( x)dx [ M ( X )] x e
2
0
2
0
2 x
dx 1 /
Среднее квадратическое отклонение
σ(X)=1/λ.
2
1
2
.

25.

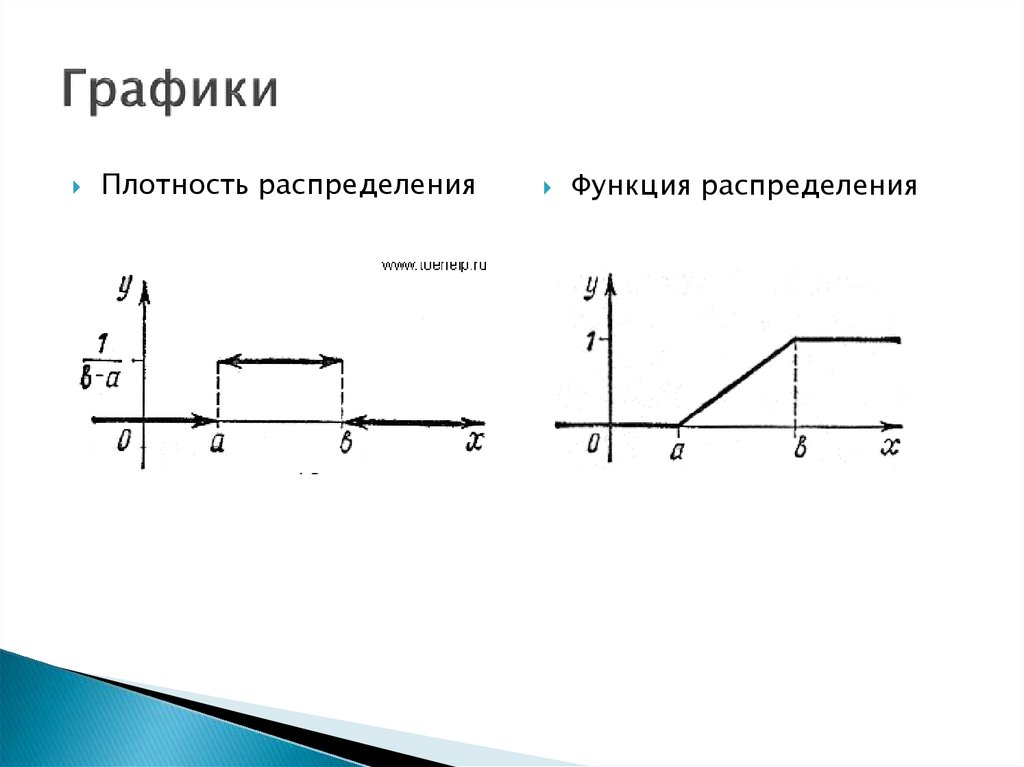
26. Определение

Непрерывная случайная
величина X, принимающая
все свои возможные
значения только на
отрезке [a, b], называется
равномерно
распределенной, если ее
при x a
0,
1
f ( x ) C
, при a x b
b
a
при x b
0,
плотность распределения
равна
Функция распределения
F(x) описывается
формулой
при x a
0,
x a
F ( x)
, при a x b
b a
при x b
1,

27. Графики

Плотность распределения
Функция распределения

28. Числовые характеристики

Математическое ожидание:
1
a b
M ( X ) xf ( x )dx
xdx
b
a
2
a
a
b
b
Дисперсия
1
a b 2 (b a ) 2
2
D( X ) x f ( x )dx [ M ( X )]
x dx [
]
.
b a a
2
12
a
b
b
2
2
Среднее квадратическое отклонение
b a
(X )
2 3

29.

30. Задача

Будем называть элементом некоторое устройство
независимо от того, «простое» оно или «сложное».
Пусть элемент начинает работать в момент времени t0=0, а
по истечении времени длительностью t происходит отказ.
Обозначим через Т непрерывную случайную величину —
длительность времени безотказной работы элемента. Если
элемент проработал безотказно (до наступления отказа)
время, меньшее t, то, следовательно, за время
длительностью t наступит отказ.

31. Задача

Таким образом, функция распределения
F (t) = P(T<t)
определяет вероятность отказа за время
длительностью t. Следовательно, вероятность
безотказной работы за это же время
длительностью t, т. е. вероятность
противоположного события Т > t, равна
R(t) = P(T>t) = 1- F(t).

32. Определение

Функцией надежности R (t) называют функцию,
определяющую вероятность безотказной работы
элемента за время длительностью t:
R(t) = P(T>t).

33.

34.

Часто длительность времени безотказной работы момента
имеет показательное распределение, функция
распределения которого определяется формулой:
F(t)=1- e -λ·t
Следовательно, функция надежности в случае
показательного распределения времени безотказной
работы элемента имеет вид:
R (t) = 1 — F (t) = 1 — (1 - e
-λ·t)
=e
-λ·t

35. Определение

Показательным законом надежности называют
функцию надежности, определяемую равенством
R (t) = e -λ·t
где λ - интенсивность отказов.
Эта формула позволяет найти вероятность безотказной
работы элемента на интервале времени длительностью t,
если время безотказной работы имеет показательное
распределение

36. Свойство закона надежности

Вероятность безотказной работы элемента на
интервале времени длительностью t не зависит
от времени предшествующей работы до начала
рассматриваемого интервала, а зависит только от
длительности времени t (при заданной
интенсивности отказов λ)

37. Пример

Время безотказной работы элемента
распределено по показательному закону
f (t) =0,02·e-0,02t при t ≥0 (t — время). Найти
вероятность того, что элемент проработает
безотказно 100 ч.

38. Пример

Время безотказной работы элемента
распределено по показательному закону
f (t) =0,02·e-0,02t при t ≥0 (t — время). Найти
вероятность того, что элемент проработает
безотказно 100 ч.
РЕШЕНИЕ.
По условию, постоянная интенсивность отказов λ=0,02.

39. Пример

Время безотказной работы элемента
распределено по показательному закону
f (t) =0,02·e-0,02t при t ≥0 (t — время). Найти
вероятность того, что элемент проработает
безотказно 100 ч.
РЕШЕНИЕ.
По условию, постоянная интенсивность отказов λ=0,02.
Воспользуемся формулой:
R (100) = е-0,02*100=е-2 = 0,13534