Охлаждение бесконечных тел. Нестационарная теплопроводность

1. Проблемы энерго- и ресурсосбережения

Охлаждение бесконечных
тел

2. Нестационарная теплопроводность

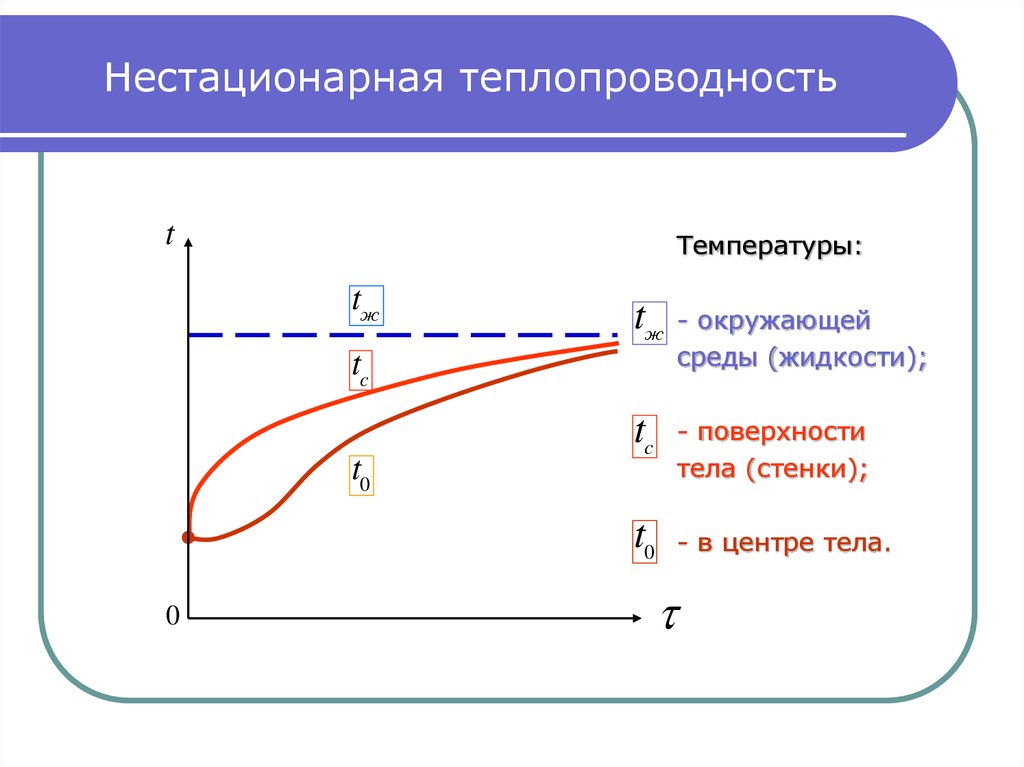
t
Температуры:
tж
tж
- окружающей
среды (жидкости);
tc
- поверхности
тела (стенки);
t0
- в центре тела.
tc
t0
0

3. Дифференциальное уравнение теплопроводности

Нестационарная теплопроводность имеет место при
нагревании и охлаждении заготовок, пуске и отключении
теплоэнергетических установок, обжиге кирпича,
вулканизации резины. На слайде показан нагрев твердого
тела в среде с температурой t Const .
ж
Процесс описывается дифференциальным уравнением теплопроводности без внутренних источников теплоты q 0.
v
2
2
2
t
t t t (1) Условия однозначности:
a( 2 2 2 ).
● геометрические; ● физические;
x y z
● начальные: при 0 t t f ( x, y, z); ( t )
(tn 0 tж ).
0
n 0
n
● граничные условия III рода:
Решение заключается в нахождении функции:
t f ( x, y, z, , , , a,to ,tж , ).

4. Охлаждение пластины

t
0
0
2
tж
t0
x

5. Начальные и граничные условия

Рассматриваем охлаждение (нагревание) пластины при:
Const;tж Const; при : 0 t t0 Const.
Подставляем избыточную температуру пластины
t tж
в дифференциальное уравнение (1) и граничные условия.
Для бесконечной пластины
Тогда дифференциальное
уравнение примет вид:
Начальные условия: при
При
Const
:
симметричная задача, тогда
граничные условия III рода:
2
:
( t / y) ( t / z) 0 .
t
2t
2
a 2; a 2 .
x
x
0 F ( x).
При : x 0 (
x (
(2)
(3)
) x 0 0;
x
) x x .
x
(4)

6. Решение

Решение дифференциального уравнения (2)
ищем в виде произведения двух функций, из
которых одна является только функцией
времени , другая – только функцией х.
f ( , x) ( ) ( x).
Подставляем (5) в (2):
(5)
( )
2 ( x)
( x) a
(
)
2
x
'( ) "( x)
a
.
'( ) ( x) a "( x) ( )
( )
( x) (6)

7. Решение

Так как левая часть уравнения (6) является только
функцией , а правая – только х, то равенство (6)
имеет место при любых их значениях. Тогда левая и
правая части этого уравнения равны константе. Пусть
это будет k 2.
1 '( )
"( x)
k 2 ,
a ( ) ( x)
'( )
ak 2 0;
( )
"( x) k 2 ( x) 0.
(7)
(8)

8. Решение

d
2
aκ 0;
dτ
d
d
2
aκ dτ
aκ 2 dτ
Решим (7)
ln -aκ τ C
2
C1e
e
- aκ 2 τ
-aκ τ c
2
;

9. Решение

Решим (8)
d x
2
dx
2
κ x 0;
2
x C2 cos κx C3 sin κx

10. Решение

Общее решение:
x, C1e
2
- aκ τ
C2 cos κx C3 sin κx
(9)

11. Решение

Решение (9) подчиним граничному условию (3):
x
C1e
x 0
-aκ 2 τ
C2 κ sin κx C3 κcos κx 0;
x 0
C2 κsin κx x 0 C3 κ cos κx x 0 C3 0
x, τ Ae
-aκ 2 τ
cos κx
(10)

12. Решение

Подчиним решение (10) граничному условию (4):
κAe
α - aκ 2 τ
sin κδ Ae
cos κδ ;
λ
α
κ sin κδ cos κδ ;
λ
-aκ 2 τ
κλ
ctg κδ .
α
(11)

13. Решение

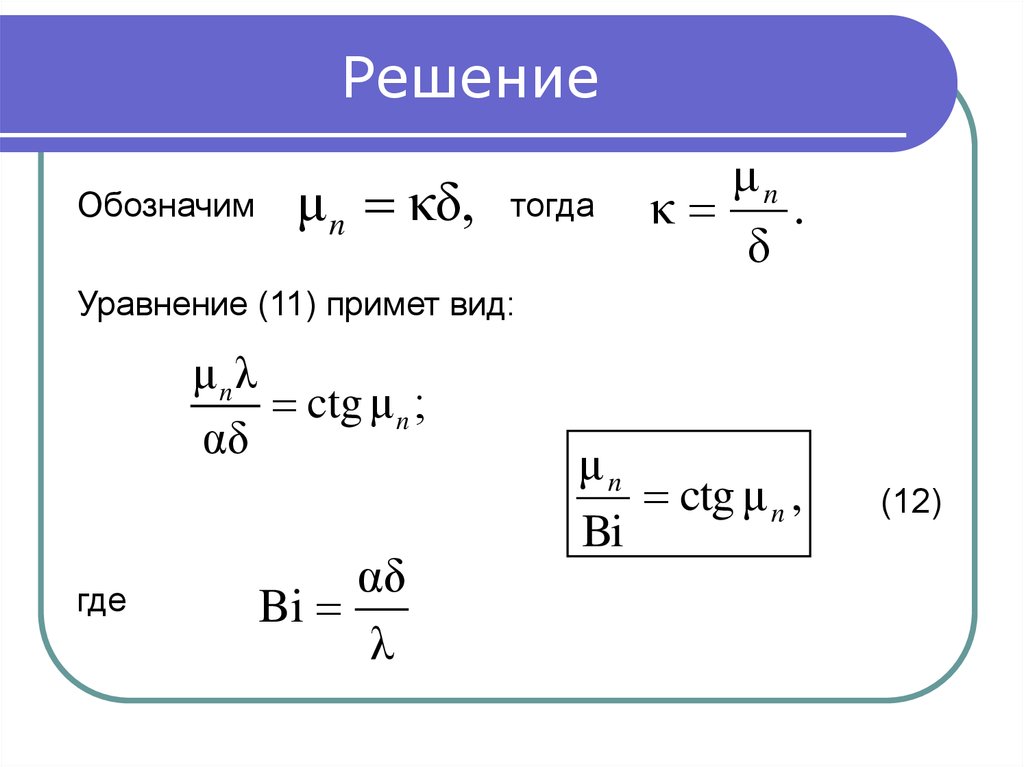
Обозначим
μ n κδ,
тогда
μn
κ
.
δ
Уравнение (11) примет вид:
μnλ
ctg μ n ;
αδ
где
αδ
Bi
λ
μn
ctg μ n ,
Bi
(12)

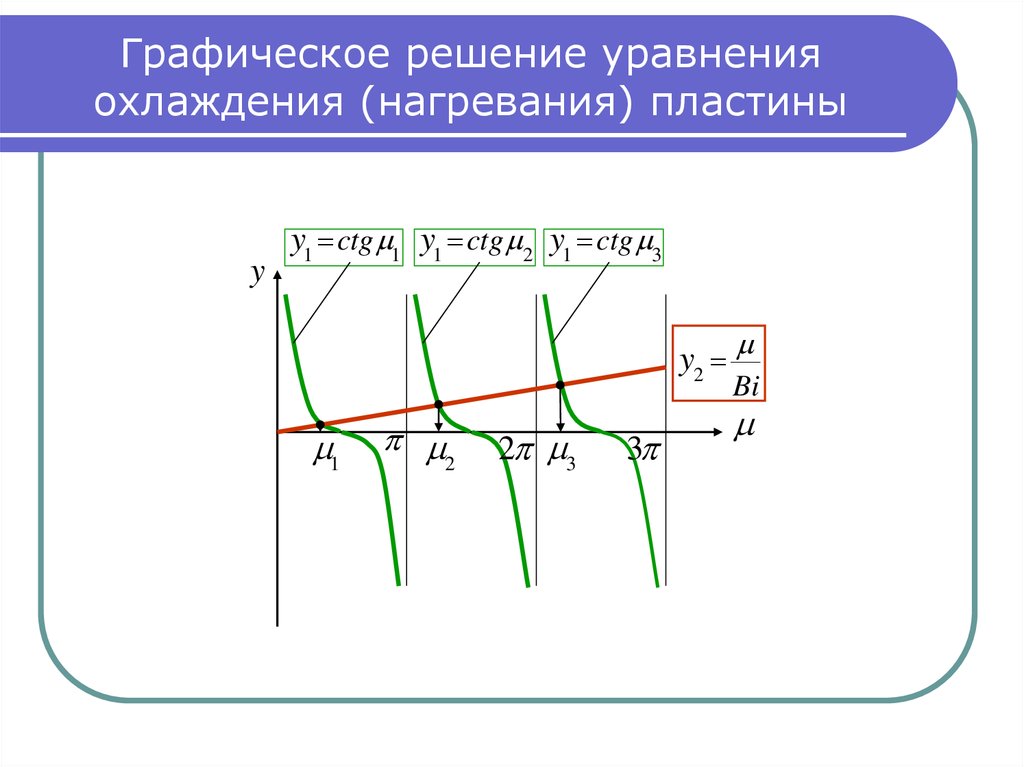
14. Графическое решение уравнения охлаждения (нагревания) пластины

y
y1 ctg 1 y1 ctg 2 y1 ctg 3
y2
Bi
1
2
2 3
3

15. Результаты графического решения

При Bi : y2
Bi
0,
то есть функция
y2
совпадает
то есть функция
y2
совпадает
3
5
1 ; 2 ; 3 ;... n (2n 1) .
2
2
2
2
с осью абсцисс, то есть:
При Bi 0: y
2
Bi
,
с осью ординат, при этом:
Каждому
i
1 0; 2 ; 3 2 ;... n (n 1) .
соответствует свое частное распределение
избыточных температур
i
, которое является решением
дифференциального уравнения (2).
Решение можно представить в виде суммы ряда
где достаточно иметь n = 4
n
i ,
1
( 1, 2, 3, 4 ) , значения которых
при Bi = 0 - ∞ приведены в таблице на следующем слайде.

16. Значения для пластины

Значения
i
для пластины
Bi
1
2
3
1,571
4,712
7,854
11.00
2,747
1,169
3,771
6,674
9,701
1,000
0,8603
3,426
6,437
9,529
0,3640
0,5885
3,253
6,341
9,463
0,0000
0,0000
3,142
6,283
9,425
4

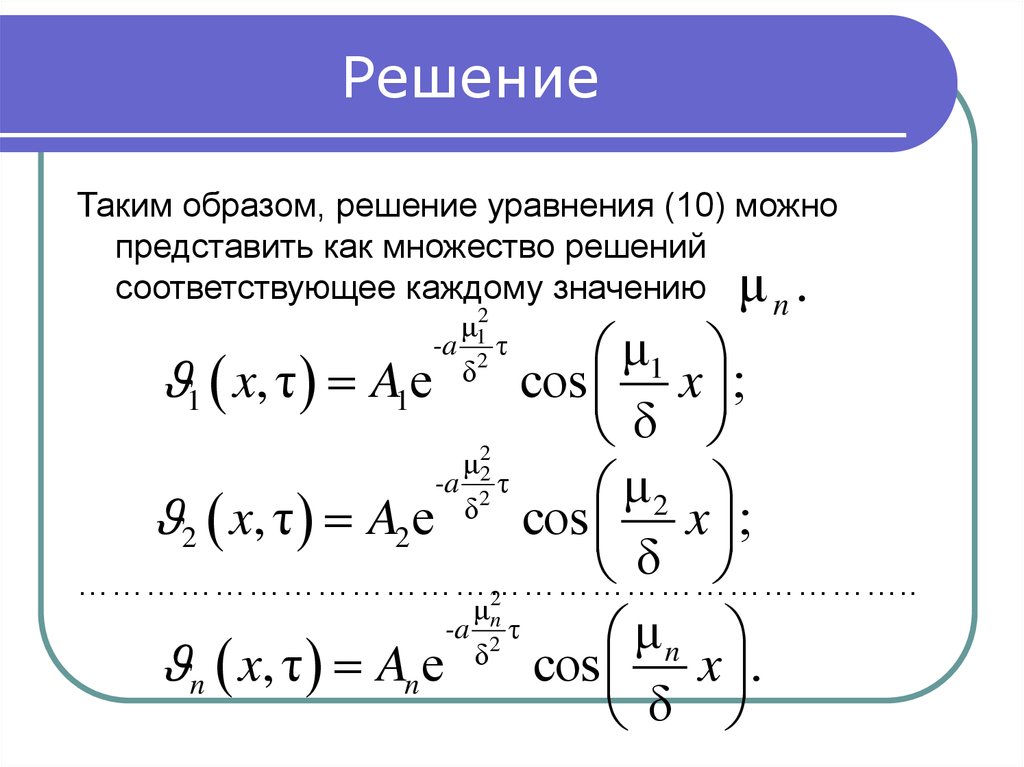
17. Решение

Таким образом, решение уравнения (10) можно
представить как множество решений
соответствующее каждому значению
n
μ12
-a 2
μ .
μ1
1 x, τ A1e
cos x ;
δ
2
μ
-a 22 τ
μ2
δ
2 x, τ A2e
cos x ;
δ
………………………………………………………………..
μ 2n
-a 2 τ
μn
δ
n x, τ An e
cos x .
δ
δ
τ

18. Решение

Решение уравнения можно представить как сумму
частных решений:
x, τ An exp μ Fo cos μ n X ,
n 1
aτ
где Fo 2
δ
x
X
δ
2
n
- число Фурье;
- безразмерная координата
(13)

19. Решение

Коэффициент An найдём из начального условия (3):
F x An cos μ n X ;
n 1
δ
μn
An
F x cos μ n X dx. (14)
δ μ n sin μ n cos μ n δ
(13) и (14) есть искомое решение задачи.

20. Температура

При Fo 0,3 можно ограничится одним членом ряда,
тогда
x, τ A1 exp μ Fo cos μ1 X ;
2
1
δ
μ1
A1
F x cos μ1 X dx.
δ μ1 sin μ1 cos μ1 δ

21. Решение

Пусть
δ
F x 0 const, тогда
x
δ 0 cos μ n δ dx
δ
sin μ n δ sin μ n
δ
2 0 sin μ n ;
μn
δ
0
μn
δ
δ

22. Решение

.
μ n 2 0δsin μ n
An
;
δ μ n sin μ n cosμ n μ n
2 0sin μ n
An
.
μ n sin μ n cos μ n

23. Температура

2 0 sin μ1
x, τ
exp μ12 Fo cos μ1 X ;
μ1 sin μ1 cos μ1
x, τ
θ x,Fo D1 exp μ12 Fo cos μ1 X ,
0
где
2sin μ1
D1
.
μ1 sin μ1 cos μ1

24. Температура

В размерном виде:
t tж
2
D1 exp μ1 Fo cos μ1 X ,
t0 t ж
2 aτ
x
t tж t0 tж D1 exp μ1 2 cos μ1
δ
δ

25. Температура

Температура в центре пластины:
2 aτ
t 0, τ tж t0 tж D1 exp μ1 2
δ
Температура на поверхности пластины:
2 aτ
t δ,τ tж t0 tж D1 exp μ1 2 cos μ1.
δ

26. Температура

Средняя температура по толщине пластины:
δ
1
t x , τ t x , τ dx
δ0
1
2 aτ δ
tж δ t0 tж D1 exp μ1 2 sin μ1 .
δ
δ μ1

27. Тепловой поток

Тепловой поток определяется по закону Фурье:
dt
q -λ
dx
2 aτ μ1
x
t0 tж D1 exp μ1 2 sin μ1 .
δ δ
δ

28. Количество теплоты

Количество теплоты, отданное пластиной в процессе
охлаждения, определяется по формуле:
Qτ 2cρδf t0 t
Полное количество теплоты, отданное пластиной за
весь период охлаждения, определяется по
формуле:
Qτ 2cρδf t0 tж

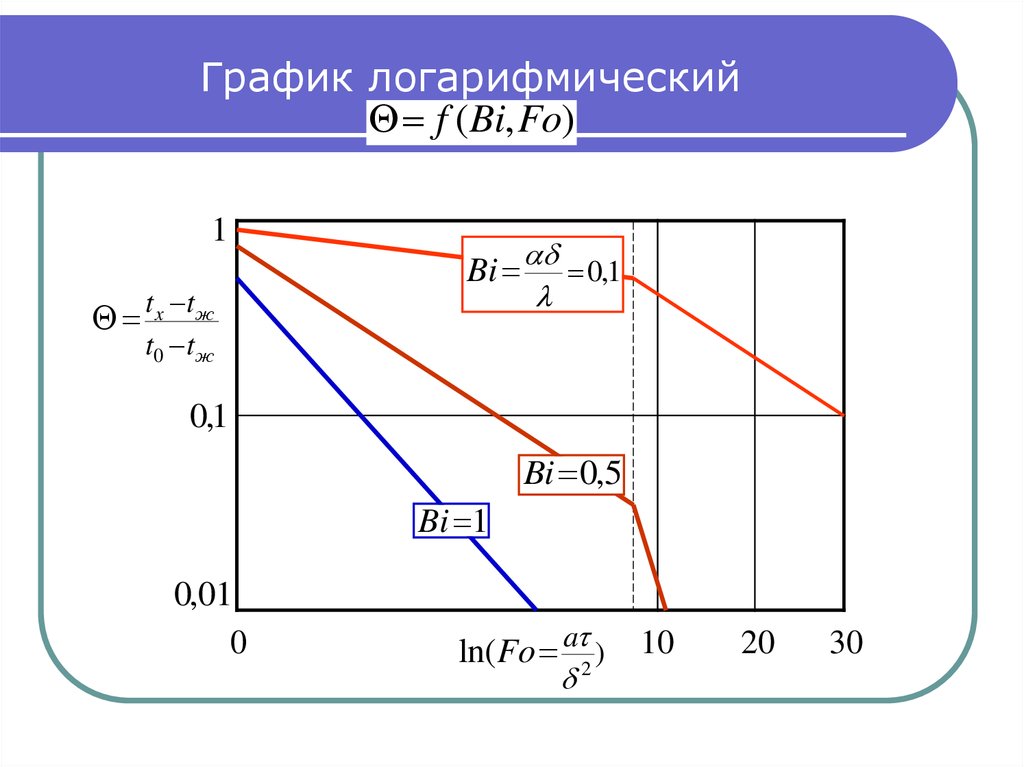
29. График логарифмический

f (Bi, Fo)
1
t x tж
t0 t ж
Bi 0,1
0,1
Bi 0,5
Bi 1
0,01
0
ln(Fo a 2 )
10
20
30

30. .

Внутренняя задача
● Частный случай (А):
Bi
(практически Bi >100): Bi – число (критерий) Био:
соотношение конвективной
/
1
(Bi
) ; 0; , теплоотдачи снаружи и теплопроводности внутри тела.
1/
В данном случае очень интенсивное наружное охлаждение,
поэтому температура поверхности пластины, погруженной
в жидкость, сразу становится равной температуре жидкости.
Распределение температур в пластине зависит от ее
теплопроводности λ и геометрических размеров
от условий внутри пластины (внутренняя задача).
.
, то есть

31. .

А) Внутренняя задача Bi
В) Внешняя задача Bi 0
.
Fo1 Fo2 Fo3
Fo 0
1
Fo 0
1
Fo1
Fo1
А)
Fo2
Fo2
.
Fo3
Fo3
0
В)
x
0
x

32. .

Внешняя задача
● Частный случай (В):
Bi 0
(практически Bi < 0,1),
Bi ( / ) 0; 0;
1/
теплопроводность (λ)
значительная.
Из-за высокого коэффициента теплопроводности пластины
температуры в ней быстро выравниваются. Охлаждение
слабое и все зависит от внешнего коэффициента
конвективной теплоотдачи
(внешняя задача).
Обозначения: - половина толщины пластины, м;
.
- теплопроводность пластины, Вт/(мК);
- коэффициент конвективной теплоотдачи, Вт/(м²К).

33. .

Внешняя задача
● Частный случай (В):
Bi 0
(практически Bi < 0,1),
Bi ( / ) 0; 0;
1/
теплопроводность (λ)
значительная.
Из-за высокого коэффициента теплопроводности пластины
температуры в ней быстро выравниваются. Охлаждение
слабое и все зависит от внешнего коэффициента
конвективной теплоотдачи
(внешняя задача).
Обозначения: - половина толщины пластины, м;
.
- теплопроводность пластины, Вт/(мК);
- коэффициент конвективной теплоотдачи, Вт/(м²К).

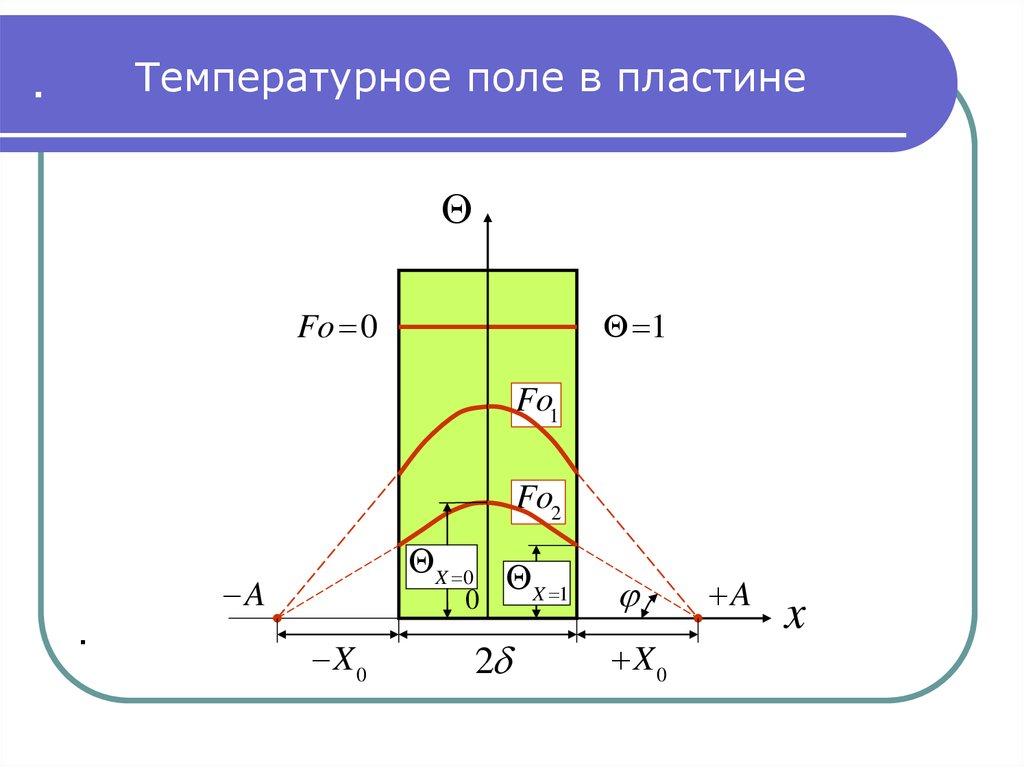
34. .

Температурное поле в пластине
.
Fo 0
1
Fo1
Fo2
.
X 0
X 1
A
0
X0
2
X0
A
x

35. Охлаждение бесконечного цилиндра

Пусть внутри источник теплоты отсутствует:
Пусть
t
t
Z
qv 0
0
Тогда дифференциальное уравнение температурного
поля примет вид:
t 1 t
t
a 2
r r
r
2
(1)

36. Охлаждение бесконечного цилиндра

Начальные условия:
t (r , 0) f (r );
Граничные условия
t (0, )
0;
r
t (r0 , )
t (r0 , ) tж ;
r
(2)
(3)
(4)

37. Охлаждение бесконечного цилиндра

Избыточная температура:
Тогда (1)-(4) примет вид:
( r , ) t ( r , ) t ж ;
2
1
a 2
;
r r
r
(r,0) f (r ) tж F (r );
(r0 , )
(r0 , );
r
(0, )
0;
r
(5)
(6)
(7)
(8)

38. Охлаждение бесконечного цилиндра

Решение ищем методом Фурье разделенных
переменных:
(r , ) (r ) ( );
Тогда уравнение (5) примет вид
1
(r ) ( ) a ( ) (r ) ( ) ( r ) ;
r
1 ( ) (r ) 1 (r )
2
const k ;
a ( ) (r ) r (r )
(9)

39. Охлаждение бесконечного цилиндра

Из (9) получим 2 уравнения:
( ) ak ( ) 0;
2
1
2
(r ) (r ) k (r ) 0;
r
(10)
(11)

40. Охлаждение бесконечного цилиндра

решение уравнения (10):
( ) C1 exp( ak );
2
решение уравнения (11):
(r ) C2 J 0 (kr ) C3 0 (kr );

41. Охлаждение бесконечного цилиндра

J 0 (kr )
0 (kr)
При
- функция Бесселя 1-го рода 0-порядка;
- функция Бесселя 2-го рода 0-порядка;
r 0 0 (kr ) C3 0

42. Охлаждение бесконечного цилиндра

Тогда решение принимает вид:
(r , ) CJ 0 (kr ) exp( ak );
2
kr0 k
r0
;
r
(r , ) CJ 0 (k ) exp( a 2 );
r0
r0
2
(12)

43. Температура

Подчинив решение (12) граничным условиям (8) получим
характеристическое уравнение для нахождения :
n
J 0 ( n )
;
Bi J1 ( n )
Решение уравнения можно представить как сумму частных
решений:
r
(r , ) Cn J 0 ( ) exp( a 2 )
r0
r0
n 1
2
(13)

44. Температура

Для нахождения Cn
используем начальные условия (6)
F (r ) Cn J 0 ( R);
n 1
r
0 rJ 0 n r0 F (r )dr
Cn r0
r
2
0 rJ 0 n r0 dr
r0
(13) и (14) есть искомое решение задачи.
(14)

45. Температура

При начальном равномерном распределении температуры:
( r , )
( r , )
0
2 J1 ( n )
r
J
(
)
exp(
a
)
0
2
2
2
r0
r0
J
(
)
J
n 1
n
0
n
1 ( n )
2

46. ОХЛАЖДЕНИЕ ШАРА

Пусть внутренние источники теплоты отсутствуют, то есть
Пусть температура изменяется только в радиальном
направлении, тогда:
2
t
t 2 t
a 2
r r
t
qv 0

47. ОХЛАЖДЕНИЕ ШАРА

Начальные условия:
Граничные условия:
t r0 ,
r
t r ,0 f r ;
t 0,
r
0;
t r0 , tж ;

48. ОХЛАЖДЕНИЕ ШАРА

Избыточная температура:
r, t r, tж
2
a 2
;
r r
r
2
F r,0 f r tж ;
0,
r
0;
r0 ,
r
r0 ,

49. Температура

Решение уравнения имеет вид:
r ,
2 a
r0
n r
Bn sin
exp n 2 ,
0
r
r0
r0
n 1
где B - коэффициент, зависящий от начальных
n
условий.
Характеристическое уравнение:
n
Bi 1
tg n

50. Температура

Или:
r ,
1
2
Bn sin( n R) exp n Fo
R
n 1

51. Вопросы к экзамену

1.
2.
Охлаждение (нагревание)
неограниченной пластины.
Охлаждение (нагревание)
бесконечно длинного цилиндра.
Охлаждение шара.