Похожие презентации:
Теплопроводность при нестационарном тепловом режиме
1. ТЕПЛОМАССООБМЕН
Теплопроводность принестационарном
тепловом режиме
Лекция № 6
2016 год
2. План
• 1. Основные положения.• 2. Нестационарная теплопроводность. Описание
процесса.
• 3. Нагрев тел с равномерным температурным
полем.
• 4. Нагрев тел с неравномерным температурным
полем. Применение теории подобия для
исследования
задач
нестационарной
теплопроводности.
3. 1. Основные положения
Если температурное поле меняется во времени, тотепловые процессы, протекающие в таких условиях,
называются нестационарными.
Нестационарные процессы теплопроводности встречаются при
охлаждении металлических заготовок, нагревание стальных слитков
в промышленных печах, в прокаливании твердых тел, в
производстве стекла, обжиге кирпича и т.д.
4.
• Передачу теплоты при нестационарном режимеможно определить, если найти закон изменения
температурного поля и теплового потока во
времени и в пространстве:
t f ( x, y, z, )
и
Q ( x, y, z, )
• где x, y, z – координаты точки; τ – время.
5.
• Указанные зависимости могут быть найдены изрешения
дифференциального
уравнения
теплопроводности Фурье:
2
2
2
t t t t
2
2 2 2 a t
c x
y
z
(1)
• При решении уравнения (1) необходимо знать
граничные условия и начальное распределение
температуры в теле.
6.
• Граничные условия задаются уравнениемt
tпов tсреды , (2)
n пов
ст
t
• где – градиент температуры на поверхности;
n пов
• α – коэффициент теплоотдачи между средой и поверхностью
твердого тела;
• λст – теплопроводность стенки;
• tпов – температура поверхности стенки;
• tсреды – температура окружающей среды.
• Физические величины
постоянными.
λ,
с,
ρ
считаются
7.
• Температура рассматриваемого тела в начальный моментвремени τ = 0 и распределена равномерно, т.е. t0=const.
• Решение уравнений (1) и (2) с учетом граничных и временных
условий дает уравнение температурного поля вида
t f ( , , a, , x, y, z, t0 , tср , l0 , l1, ..., ln ). (3)
• Из уравнения (3) показывает, что температура
зависит от большого числа переменных и постоянных
параметров.
• Решение уравнения (3) представляет собой очень
сложную математическую задачу.
8.
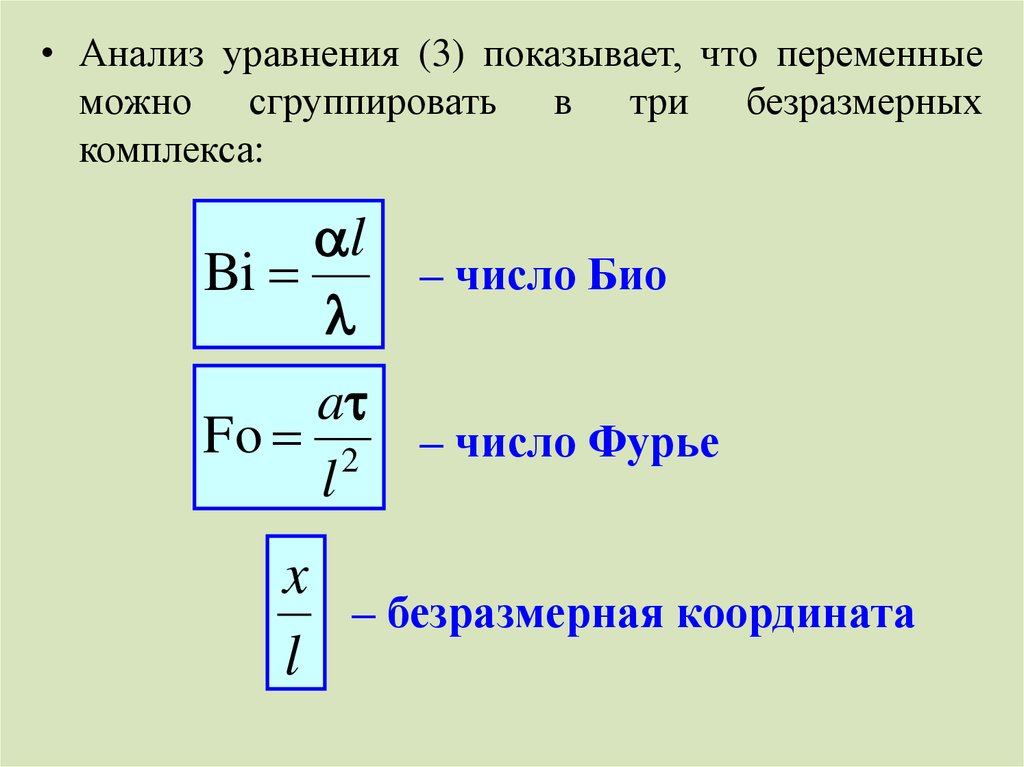
• Анализ уравнения (3) показывает, что переменныеможно сгруппировать в три безразмерных
комплекса:
l
– число Био
Bi
a
Fo 2 – число Фурье
l
x
l
– безразмерная координата
9. Число Био (критерий Био)
lBi
• где l – характерный размер тела (м); λ – коэффициент
теплопроводности твердого тела; α – коэффициент теплоотдачи
между средой и поверхностью твердого тела.
• Критерий Био характеризует соотношение между внутренним
и внешним термическими сопротивлениями.
• – внутреннее термическое сопротивление;
l
1
• – внешнее термическое сопротивление.
10. Число Фурье (критерий Фурье)
aFo 2
l
• где l – характерный размер тела (м);
• a – температурапроводность;
• τ – время.
• Критерий Фурье характеризует связь
скоростью
изменения
температурного
физическими константами и размерами тела.
между
поля,
11.
• Искомая функция в виде безразмерной температуры1
может быть представлена следующим уравнением:
x
f Fo,Bi,
1
l
• ϑ – избыточная температура тела, т.е. температура
отсчитанная от температуры окружающей среды
tтела tо. ср .
12. 2. Нестационарная теплопроводность. Описание процесса
Рассмотрим нестационарные тепловые процессы прикоторых температурное поле изменяется во временем,
т.е. является функцией от времени.
Нестационарность тепловых процессов обусловлена
изменением энергии тела и всегда связана с явлениями
прогрева или охлаждения тела.
13.
Тело внесли в среду с более высокойтемпературой
• Сразу возникает процесс теплообмена между средой
и телом.
• Тело начинает прогреваться.
• Сначала
нагреваются
поверхностные
слои,
постепенно процесс прогрева распространяется в
глубь тела.
14.
Тело внесли в среду с более высокойтемпературой.
• О характере изменения температуры
тела
за
время
прогрева
дают
представление кривые на рисунке а.
tс – температура на поверхности тела;
tо – температура в центре тела;
tж – температура окружающей среды.
По истечении некоторого времени (теоретически бесконечно
большого) температура всех частей тела выравнивается и
становится равной температуре окружающей среды и наступает
тепловое равновесие.
15.
При нестационарном процессеинтенсивность подвода теплоты
также не постоянна во времени.
• О характере изменения подвода
теплоты
дает представление
кривая на рисунке б.
По
мере
прогрева
тела
интенсивность передачи теплоты
постепенно уменьшается и в пределе
становится равной нулю.
16.
Площадь, заключенная между осямии кривой, определяет полное
количество теплоты, переданное за
время τ.
Эта теплота аккумулируется телом и
идет на повышение его энергии.
Аналогичным образом протекает процесс
охлаждения тела.
При этом энергия тела уменьшается, а
выделенная
теплота
передается
в
окружающую среду.
17.
Рассмотрим процесс теплопередачичерез стенку.
Вначале процесс был стационарным.
• Температура горячей среды t’ж1,
• холодной – t’ж2,
• температуры поверхностей стенки t’с1 и
t’с2 (рисунок в).
• Если изменить режим теплопередачи,
например,
сразу
резко
повысить
температуру горячей среды до t”ж1, то на
некоторое время процесс становится
нестационарным.
18.
Рассмотрим процесстеплопередачи через стенку.
Температурная кривая t’ж1 – t’с1 – t’с2 –
t’ж2 будет изменяться до тех пор, пока
снова не установится стационарный
режим t”ж1 – t”с1 – t”с2 – t”ж2.
19.
Изменение во времени t’с1 и t’с2представлено на рисунке г.
О характере изменения количества
передаваемой
теплоты
для
рассматриваемого
случая
дают
представление кривые на рисунке д.
Q’ и Q” – тепловые потоки при
стационарных режимах,
Q1 и Q2 – тепловые потоки через
горячую и холодную поверхности
стенки при нестационарном режиме.
20.
Q’ и Q” – тепловые потоки пристационарных режимах,
Q1 и Q2 – тепловые потоки через
горячую и холодную поверхности
стенки при нестационарном режиме.
Заштрихованная
площадка
представляет собой количество
теплоты, затраченное на изменение
энергии стенки (аккумулированная
теплота).
21.
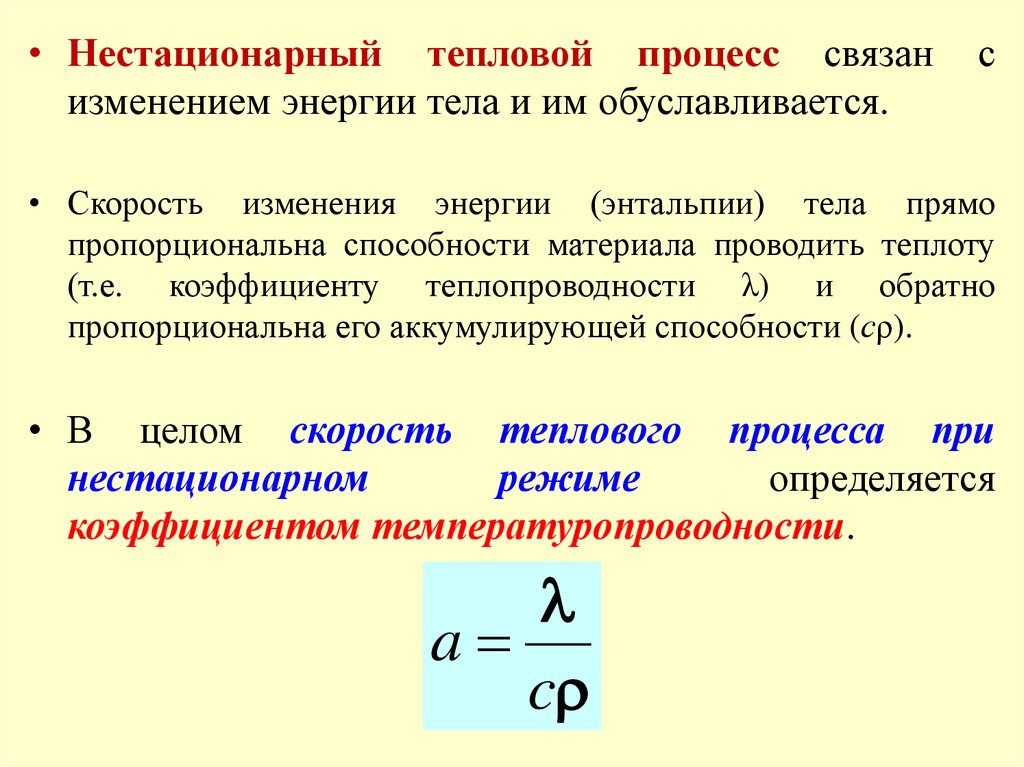
• Нестационарный тепловой процесс связанизменением энергии тела и им обуславливается.
с
• Скорость изменения энергии (энтальпии) тела прямо
пропорциональна способности материала проводить теплоту
(т.е. коэффициенту теплопроводности λ) и обратно
пропорциональна его аккумулирующей способности (сρ).
• В целом скорость теплового процесса при
нестационарном
режиме
определяется
коэффициентом температуропроводности.
a
c
22.
• Рассмотренный характер изменения температуры иколичества переданной теплоты справедлив лишь
для твердых тел.
• При нагреве жидких и газообразных тел в общем
случае неизбежно возникает конвекция, которая
способствует выравниванию температуры.
• В этих случаях можно говорить об изменении во
времени лишь средней температуры жидкости.
23.
• Решитьзадачу
нестационарной
теплопроводности – это значит найти зависимости
изменения
температуры
и
количества
переданной теплоты во времени для любой точки
тела.
• Такие зависимости получаются путем решения
дифференциального уравнения теплопроводности.
24. 3. Нагрев тел с равномерным температурным полем
А) Тепло на поверхность передается конвекцией.Б) Тепло на поверхность передается излучением.
25. А) Тепло на поверхность передается конвекцией
• Количество теплоты переданное от среды кповерхности тела конвекцией найдем используя
закон Ньютона – Рихмана
QT (tсреда t ) Fd ,
dτ – промежуток времени
передается теплота;
t – температура тела (стенки).
в
течении
(1)
которого
26.
• Теплота воспринимаемая телом:QT Mcdt ,
(2)
• где M – масса тела;
• с – удельная теплоемкость тела;
• dt – изменение температуры тела.
• В уравнениях (1) и (2) левые части равны,
следовательно равны и правые части. Приравняем
их:
среда
(t
t ) Fd Mcdt
27.
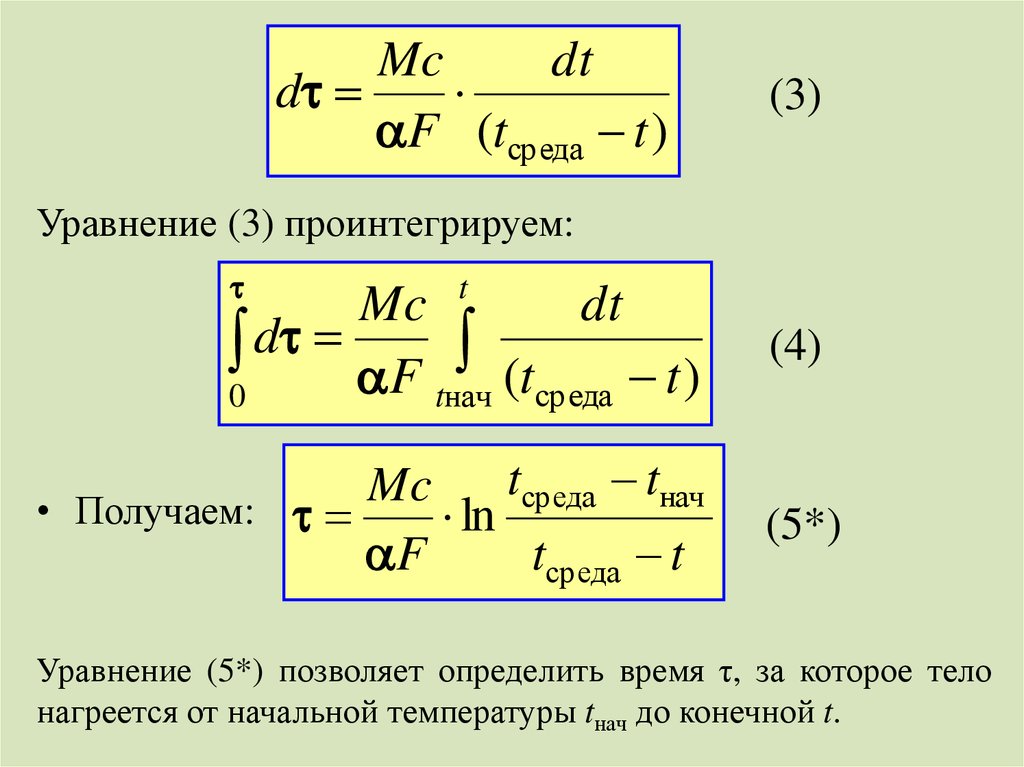
Mcdt
d
F (tсреда t )
(3)
Уравнение (3) проинтегрируем:
t
Mc
dt
d F (t t )
0
tнач среда
tсреда tнач
Mc
• Получаем:
ln
F
tсреда t
(4)
(5*)
Уравнение (5*) позволяет определить время τ, за которое тело
нагреется от начальной температуры tнач до конечной t.
28.
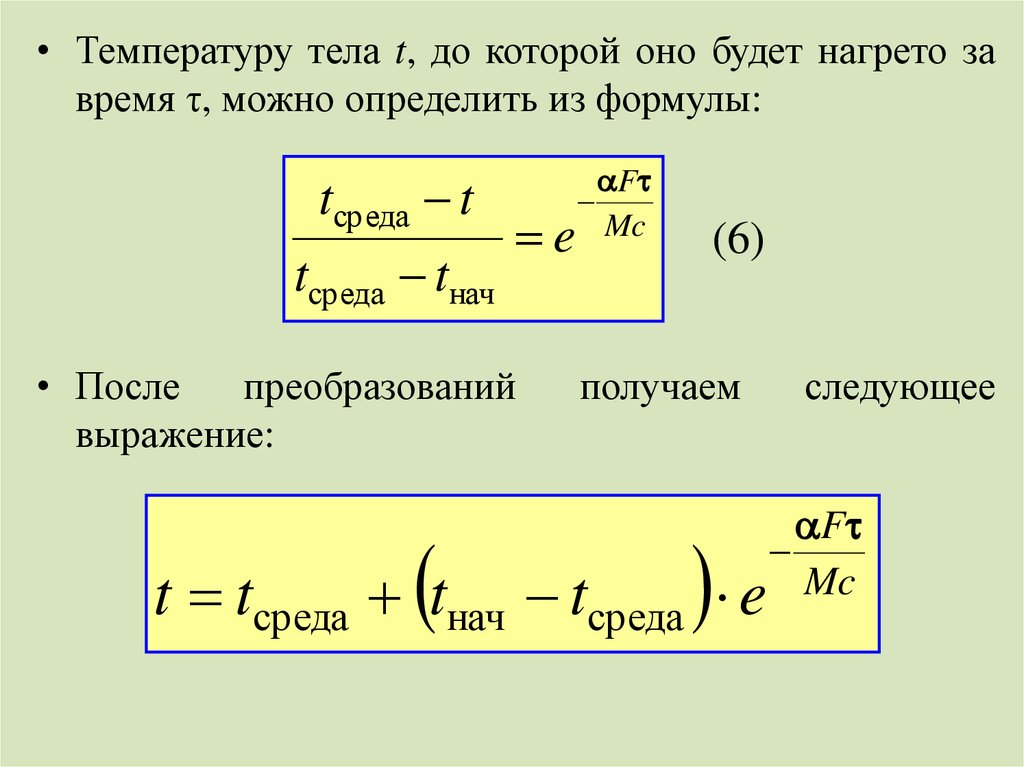
• Температуру тела t, до которой оно будет нагрето завремя τ, можно определить из формулы:
tсреда t
tсреда tнач
• После
преобразований
выражение:
F
e Mc
(6)
получаем
t tсреда tнач tсреда
следующее
F
e Mc
29. Б) Тепло на поверхность передается излучением
• Количество теплоты переданное от среды кповерхности тела излучением найдем используя закон
Стефана - Больцмана
4
QT пр (Tсреда
T ) Fd ,
4
• где σпр – приведенный коэффициент излучения.
• Теплота воспринимаемая телом:
QT McdT .
(2)
(1)
30.
• В уравнениях (1) и (2) левые части равны,следовательно равны и правые части. Приравняем их:
4
пр (Tсреда
T ) Fd McdT
4
Mc
dT
d
4
4
пр F (Tсреда T )
(3)
• Уравнение (3) проинтегрируем:
T
Mc
dT
d F (T 4 T 4 )
пр
0
Tнач
среда
(4)
31.
• При лучистой теплоотдаче на поверхность телапродолжительность
нагрева
определяется
по
формуле:
T
Tнач
1
1
T
T
Mc
1
T
T
среда
среда
3 ln
2arctg
ln
2arctg нач .
пр F Tсреда 1 T
Tсреда 1 Tнач
Tсреда
T
T
среда
среда
(4а)
• Формулы (5*) и (4а) показывают, что время нагрева тонкого
тела прямо пропорционально его массе и теплоемкости и
обратно пропорционально величине тепловоспринимающей
поверхности и интенсивности передачи тепла к ней.
• Скорость нагрева тонкого тела зависит только от условий
подвода к нему тепла.
32. 4. Неограниченная пластина
Рассмотрим охлаждение плоской пластины толщиной2δ (l = δ).
Размеры пластины в направлении координатных осей
Oy и Oz бесконечно велики.
Пластина омывается с обеих сторон жидкостью или
газом с α = const.
33.
В начальный момент времени τ = 0 пластина:имеет во всех своих точках постоянную
температуру t0;
избыточная температура ϑ1 = t0 – tо. ср.;
будет постоянной для всех точек тела.
Заданы:
коэффициент теплопроводности λст;
плотность тела ρ;
удельная теплоемкость тела с.
Все эти величины постоянны.
34.
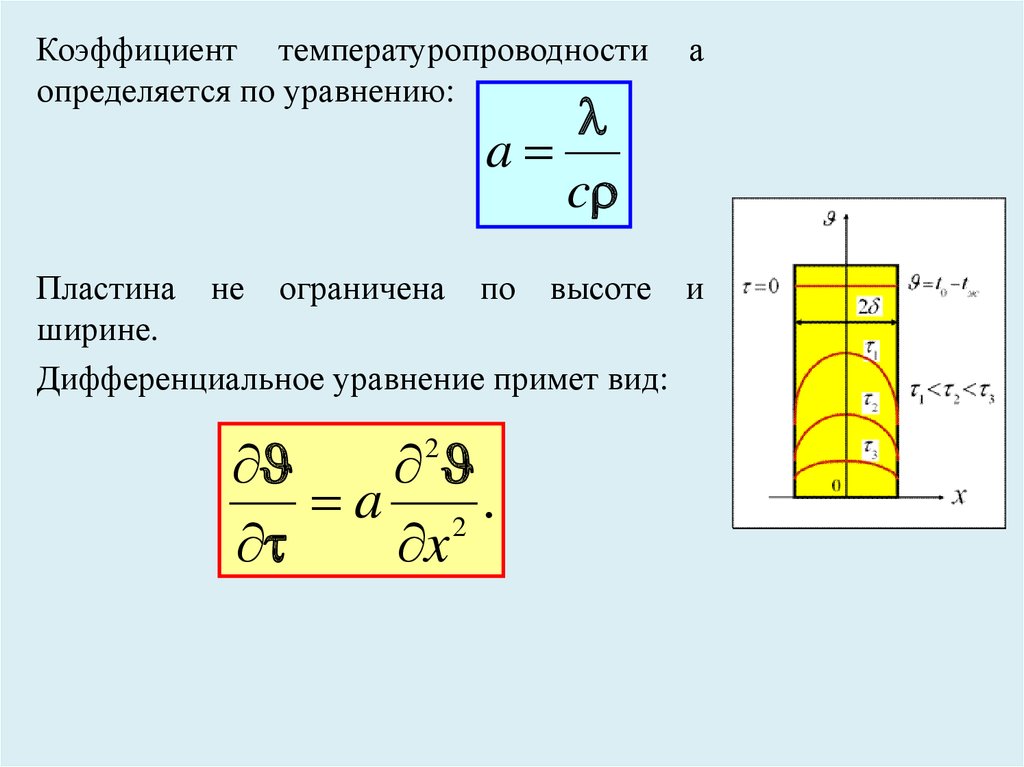
Коэффициент температуропроводностиопределяется по уравнению:
а
a
c
Пластина не ограничена по высоте и
ширине.
Дифференциальное уравнение примет вид:
a 2.
x
2
35.
Граничное условие при x = ± δст
ст
x x
И начальное условие при τ = 0
1
Температуры поверхности стенки и в ее
средней плоскости сечения определяются из
соотношения
l a
tст tо. ср
f
, 2 f Bi, Fo (1)
1 t0 tо. ср
ст l
36.
• Безразмерная координата x/l в средней плоскости ина поверхности пластины становится постоянной
величиной
при x = 0 x/l = 0;
при x = δ x/l = 1;
и поэтому отсутствует в уравнении (1).
• Для средней плоскости надо заменить tст на
температуру в середине tцентр.
ц tцентр tо. ср
f1 Bi, Fo
1
t0 tо. ср
(2)
37.
•Количество теплоты, отдаваемой пластиной вокружающую среду за время τ, должно быть равным
изменению внутренней энергии тела за период полного
его охлаждения (нагревания).
•Начальная внутренняя энергия пластины, отсчитанная
от внутренней энергии при температуре среды tо. ср.,
окружающей стену, как от нуля, равна
Q0 2Fc t0 tо. ср 2Fc 1
(3)
38.
• Количествотеплоты,
выделяющейся
при
охлаждении
пластины,
определяется
также
безразмерными числами Bi и Fo:
Q
f 2 Bi, Fo
Q0
(4)
Q 2 Fc t0 tср. ст
где Qτ – количество теплоты, переданное в
окружающую среду за время τ;
tср. ст – средняя температура стенки по истечению
промежутка времени τ.
39.
• Зависимости (1), (2) и (4) даются в виде графиков(номограммы Будрина) или в виде таблиц.
• Таблицы позволяют
точностью.
решать
задачи
с
большей
• Сначала вычисляются числа Bi и Fo.
• Затем определяют
ц ст Q
,
, .
1 1 Q0
• Поскольку t0 – tо. ср. и начальное теплосодержание
известны, то легко вычисляются tст, tц и Qτ.


































 Физика
Физика








