Похожие презентации:
Параметрические критерии проверки однородности средних
1. Параметрические критерии проверки однородности средних
Лекция №7для студентов 2 курса,
обучающихся по специальности 060609 –
Медицинская кибернетика
доц. Шапиро Л.А.
Красноярск, 2015 г.
2. План лекции:
1. Актуальность темы. Проверка простыхгипотез о параметрах.
2. Сравнение выборочной средней с
гипотетической генеральной средней
нормальной совокупности.
3. Сравнение двух средних по зависимым
выборкам малого объема из нормальных
генеральных совокупностей.
4. Сравнение генеральных средних двух
групп по независимым выборкам из
нормальных совокупностей.
3. Проверка простых гипотез о параметрах
4.
Сравнение выборочной средней с гипотетическойгенеральной средней нормальной совокупности.
Алгоритм может быть использован при проверке соответствия
теории и эксперимента: в этом случае a-предсказанное теорией
значение некоторой величины, выборка х1, х2, ..., xn-результаты
экспериментального определения той же величины.
Этим же приемом пользуемся, чтобы показать, что средство или
метод измерения не дают систематической погрешности. В этом
случае a - действительное значение некоторой величины (свойство
стандартного образца или результат измерения заведомо точным
прибором, или мировая постоянная), выборка х1, х2,..., xn – ряд
результатов, полученных аттестуемым методом (средством)
измерения.
5.
1. Дисперсия генеральной совокупности известна.Генеральная средняя неизвестна, но предполагается
равной а0. Пусть из нормальной генеральной
совокупности извлечена выборка объемом n и по ней
найдена выборочная средняя
причем генеральная
дисперсия 2 известна. Требуется по выборочной
x
средней проверить нулевую гипотезу Н0: а=а0. Т.к.
выборочная средняя является несмещенной оценкой
генеральной средней:
М( )=а, нулевая гипотеза: Н0: М( )= а0
x
x
6.
т.е. надо установить значимо или незначимоотличаются выборочная и генеральная средняя. В
качестве критерия служит величина:
( X a 0 ) ( X a 0 ) n
U
(X )
x
которая распределена нормально, причем M(U)=0,
(U)=1.
а) Н0: а= а0
Н1: а а0
Вычисляем наблюдаемое (эмпирическое) значение
критерия:
U набл
( x a 0 ) n
7.
по таблице функции Лапласа найдем критическую точкудвусторонней критической области по равенству:Ф(uкр)=(1- )/2
Если |Uнабл|<uкр нет оснований отвергнуть нулевую гипотезу
Если |Uнабл|>uкр нулевую гипотезу отвергают
б) Н0: а= а0
Н1: а> а0
Ф(uкрправ)=(1-2 )/2
Если Uнабл<uкр нет оснований отвергнуть нулевую гипотезу
Если Uнабл>uкр нулевую гипотезу отвергают
в) Н0: а= а0
Н1: а< а0
Сначала находим Ф(uкрправ)=(1-2 )/2 uкрлев=- uкрправ
Если Uнабл>-uкр нет оснований отвергнуть нулевую гипотезу
Если Uнабл<-uкр нулевую гипотезу отвергают
8.
Пример1. Из нормальной генеральной совокупности извлеченавыборка объемом n=36 и по ней найдена выборочная средняя
=21,6, =0,36. Требуется xпри уровне значимости 0,05 проверить
нулевую гипотезу Н0: а=а0=21. Н1: а а0
Решение:
( x a 0 ) n
(21,6 21) 36
U набл
10
0,36функции Лапласа
Ф(uкр)=(1- )/2=(1-0,05)/2=0,475.
По таблице
найдем uкр=1,96
Т.к. Uнабл>uкр (10>1,96) нулевую гипотезу отвергаем-выборочная
и генеральная средняя отличаются значимо
9.
2. Дисперсия генеральной совокупности неизвестна(например, при малых выборках).
В качестве критерия принимают СВ Т, которая имеет
распределение Стьюдента с k=n-1 степенями свободы:
а) Н0: а= а0
( X a 0 ) n
T
Н1: а а0
S
Вычисляем наблюдаемое (эмпирическое) значение
критерия:
( x a 0 ) n
Tнабл
s
По таблице Стьюдента для уровня значимости и числа
степеней свободы k=n-1 находим двустороннее критическое
значение tкрдвуст
10.
Если |Tнабл|<tкрдвуст нет оснований отвергнуть нулевую гипотезуЕсли |Tнабл|>tкрдвуст нулевую гипотезу отвергают
б) Н0: а= а0
Н1: а> а0
По таблице Стьюдента для уровня значимости /2 и числа
степеней свободы k=n-1 находим
tкрправ.
Если Tнабл<tкрправ нет оснований отвергнуть нулевую гипотезу
в) Н0: а= а0 Н1: а< а0
Находим вспомогательную критическую точку tкрправ.
tкрлев=- tкрправ
Если Tнабл>-tкрпр нет оснований отвергнуть нулевую гипотезу
Если Tнабл<-tкрпр нулевую гипотезу отвергают
11.
Пример: По выборке объема n=20, извлеченной изнормальной генеральной совокупности, найдена выборочная
средняя x =16 и исправленное s=4,5.
При уровне значимости 0,05 проверить нулевую гипотезу Н0:
а=а0=15 при конкурирующей гипотезе:
Н1: а 15
Решение: Критическая область двусторонняя.
( x a 0 ) n (16 15) 20
Tнабл
0,99
s
4,5
tкрдвуст (0,05;19)=2,09
0,99<2,09 - нет оснований отвергнуть нулевую гипотезу, выборочная
средняя незначимо отличается от гипотетической генеральной
средней
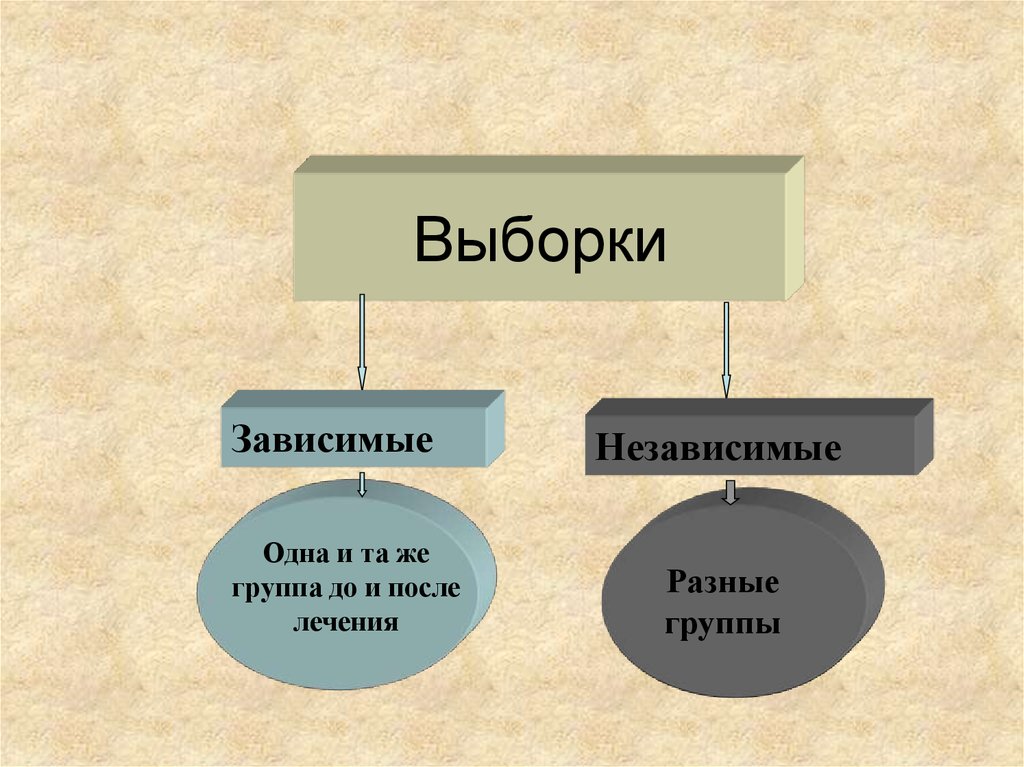
12. Выборки
ЗависимыеОдна и та же
группа до и после
лечения
Независимые
Разные
группы
13. Критерий Стьюдента
Для двухвыборок
Для одной
выборки
Независимые
выборки
С одинаковыми
дисперсиями
С различными
дисперсиями
Зависимые
выборки
14. Критерий tнабл для определения достоверности средней арифметической одной выборки
tнаблx 0
sx
tнабл< tкр (df, α=0,05) выборка однородна
tнабл> tкр (df, α=0,05)
выборка не однородна – проверить на выскакивающие
результаты
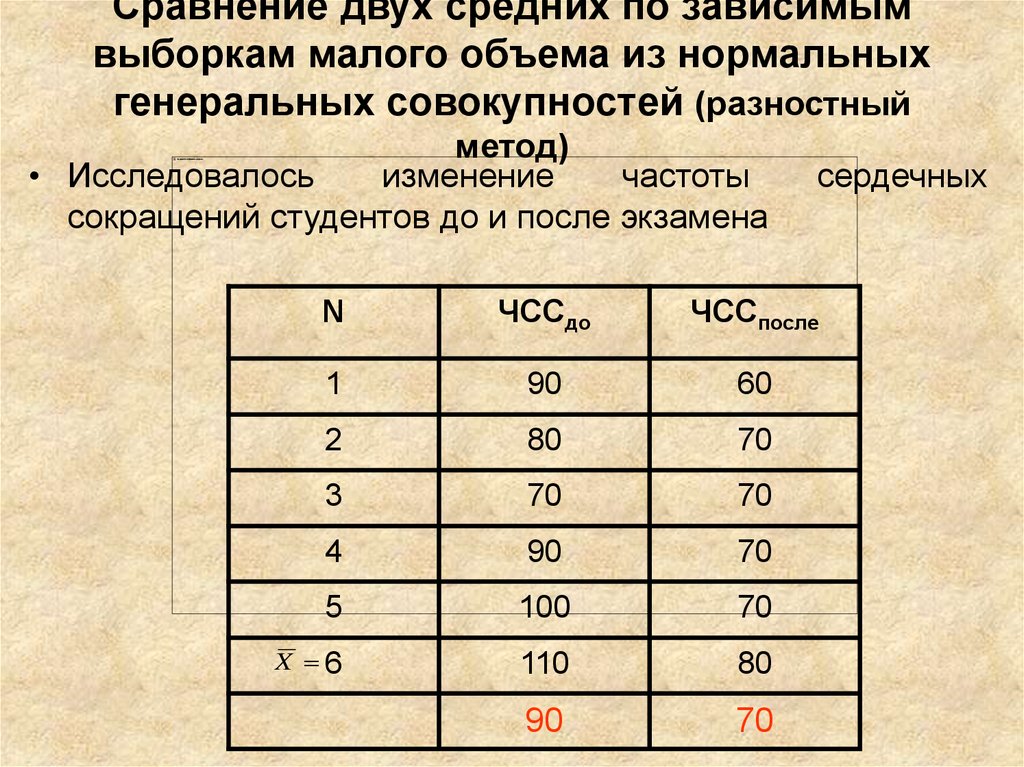
15. Сравнение двух средних по зависимым выборкам малого объема из нормальных генеральных совокупностей (разностный метод)
• Исследовалосьизменение
частоты
сокращений студентов до и после экзамена
сердечных
N
ЧССдо
ЧССпосле
1
90
60
2
80
70
3
70
70
4
90
70
5
100
70
X 6
110
80
90
70
16.
1. Найдем среднее арифметическое значениевыборки:
n
x
x1 x2 ... x6
x до
n
n
90 70 80 90 100 110
90
6
2. Вычислим дисперсию (рассеивание ряда)
i 1
i
n
D( x ) s
2
2
(
x
x
)
i
i 1
n 1
где df = n-1
число степеней свободы
(90 90) 2 (80 90) 2 ... (110 90) 2
D( x)
200
5
17.
3. Среднее квадратическое отклонениевыборки:
s D 200 14,1
Это
- точечные (т.е. выраженные одним
значением) параметры малой выборки.
Результат записывается в виде:
x s 90 14,1( уд / мин)
18.
4.Определим
ошибку:
среднюю
квадратическую
s 14,1
sx
5,8
n
6
5. Определим доверительный интервал для генеральной
средней.
По таблицам Стьюдента находим t для доверительной
вероятности 0,95 и числа степеней свободы df=n-1=5: t=2,57,
следовательно:
=90 2,57 5,8=90 15 уд/мин
или 75 105 уд/мин
19.
• Для второго ряда измерений:60 70 ... 80
xпосле
70
6
(70 60) 2 (70 70) 2 ... (80 70) 2
D( x)
40
5
s 40 6,3
6,3
sx
2,58
6
20. Нулевая гипотеза:
В генеральной совокупности нет различиямежду средними арифметическими выборок
Проверяем гипотезу по критерию Стьюдента t
при уровне значимости =0,05.
1. Определяем tнабл:
d
tнабл
sd
где d-среднее значение разности
пульса до и после экзамена
sd-стандартная ошибка разности
21. Нулевая гипотеза:
2. Определяем критическое значениекритерия Стьюдента (tкр)для =0,05 и
df=n-1
Если tнабл ≥ tкр нулевая гипотеза
отвергается, различие средних
статистически значимо
Если t набл < tкр, нулевая гипотеза
принимается, различие средних
статистически не значимо
22.
NЧССдо
ЧССпосле
d
(d-dср)2
1
90
60
-30
100
2
80
70
-10
100
3
70
70
0
400
4
90
70
-20
0
5
100
70
-30
100
6
110
80
-30
100
dср=-20
D=160
90
70
23. Для разности:
( 30) ) ( 10) ... ( 30)d
20
6
( 30 ( 20) 2 ... ( 30 ( 20) 2
D( x)
160
5
s 160 12,65
12,65
sd
5,16
6
24.
• Определим, достоверно ли определенасредняя арифметическая разности:
d
20
t набл
3,87
sd 5,16
tкр(0,05;5)=2,57 tнабл> tкр
Это означает, что нулевая гипотеза отвергается,
снижение ЧСС статистически значимо
25.
ЧСС ( X S )Группа
МК201
(n=6)
До экзамена
90±14,1
уд/мин
После
экзамена
70 ±6,3*
Примечание:*-значимость различий <0,05
Рассчитаем эффект:
(70 90)
*100% 22%
90
ЧСС студентов после экзамена
снизилась на 22% ( <0,05)
26. Сравнение генеральных средних двух групп по независимым выборкам из нормальных совокупностей.
Допущения:• В генеральной совокупности выборки
распределены по нормальному закону
• Дисперсии независимых выборок
однородны (критерий Фишера)
D1
F
D2
27.
• Нормированное отклонение:x1 x2 d
tнабл
sx1 x2
sd
1. Для n 30, ошибка разницы sd определяется по
формуле:
tнабл
Пример: n1=40
Х1 Х 2
S x21 S x22
n2=50
x1 150 x2 140 sx 20 sx 30
1
2
Определить значимость различий при α=0,05
28.
d150 140
tнабл= s
=0,277
2
2
20 30
d
tкрит (0,05)=1,96, tнабл< tкрит.
Разница средних арифметических недостоверна.
2. Для n<30, ошибка разницы sd определяется по
формуле:
( x1i x1 ) x 2i x 2 n1 n 2
sd
2
(n1 1) (n 2 1)
2
n1 n 2
29.
Сравним изменение частоты сердечныхсокращений студентов МК201 и МК202
группы до экзамена
МК201
МК202
Δ Х1
(Δ Х1)2
Δ Х2
(Δ Х2)2
90
100
0
0
0
0
80
120
-10
100
20
400
70
90
-20
400
-10
100
90
70
0
0
-30
900
100
90
10
100
-10
100
110
110
20
400
10
100
20
400
120
X1
90
X2
=
1000
100
D1=
1000/5=
200
2000
D2=
2000/6
=333
30. df=(n1-1)+(n2-1)=11
Fнабл333
1,67
200
Fкрит(6,5,0,05)=4,95
1,67<4,95 дисперсии
однородны.
(1000 2000 ) 13
Sd
9,2
(5 6) 42
tнабл
10
1,1
9,2
df=(n1-1)+(n2-1)=11
tнабл< tкр , нулевая гипотеза не
tкр=2,2
отвергается, различие средних
арифметических статистически не
значимо, выборки принадлежат
одной генеральной совокупности
31.
ГруппаПоказатель
(X S)
ЧСС
(уд/мин)
МК201
МК202
90±14,1
(6)
100 ±18,3
(7)
32. Сводка основных формул
Средняя арифметическая выборкиn
xi
x1 x 2 ... x n
i 1
x
n
n
n
Дисперсия
2
D( x )
(x
i 1
i
x)
n 1
Среднее квадратическое отклонение
s D(х)
Средняя квадратическая ошибка:
s
sx
n
33.
Критерий нормированного отклонения(по Стьюденту)
x a
t
sx
Доверительный интервал для генеральной
средней
t ,n sx
Критерий tнабл для определения
достоверности средней арифметической
одной выборки
x
tнабл
sx
34.
• Критерий tэксп разности среднихарифметических двух выборок
а) n≥30
t экспер
Х1 Х 2
S x21 S x22
б) n<30
t экспер
Х1 Х 2
( X
2
2
X
)
(
X
X
)
n n2
1i
1
2i
2
1
( n1 1) ( n2 1)
n1 n2
35. Заключение
Нами рассмотрены критерии проверкиоднородности средних по выборкам
из нормальных совокупностей.
36. РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА:
Основная литература:Попов А.М. Теория вероятней и математическая
статистика /А.М. Попов, В.Н. Сотников. – М.: ЮРАЙТ,
2011. – 440 с.
Гмурман В. Е. Теория вероятностей и
математическая статистика: учебное пособие / В.Е.
Гмурман. – М. : Высш. шк., 2011. – 479 с.
Гмурман В. Е. Руководство к решению задач по
теории вероятностей и математической статистике /
В.Е. Гмурман. – М. : Высш. шк., 2011. – 404 с.
Балдин К. В. Основы теории вероятностей и
математической статистики : учебник / К. В. Балдин. –
М. : Флинта, 2010. – 488с.
Учебно–методические пособия:
Шапиро Л.А., Шилина Н.Г. Руководство к
практическим занятиям по медицинской и
биологической статистике Красноярск: ООО
«Поликом». – 2003.



































 Математика
Математика








