Похожие презентации:
Построение графика функции
1. Постройте график функции
Х – 1,f(x)=
если -5 ≤ x ≤ 0,
(x – 1)2 – 2, если 0 < x ≤ 3,
2,
если 3 < x ≤ 5.
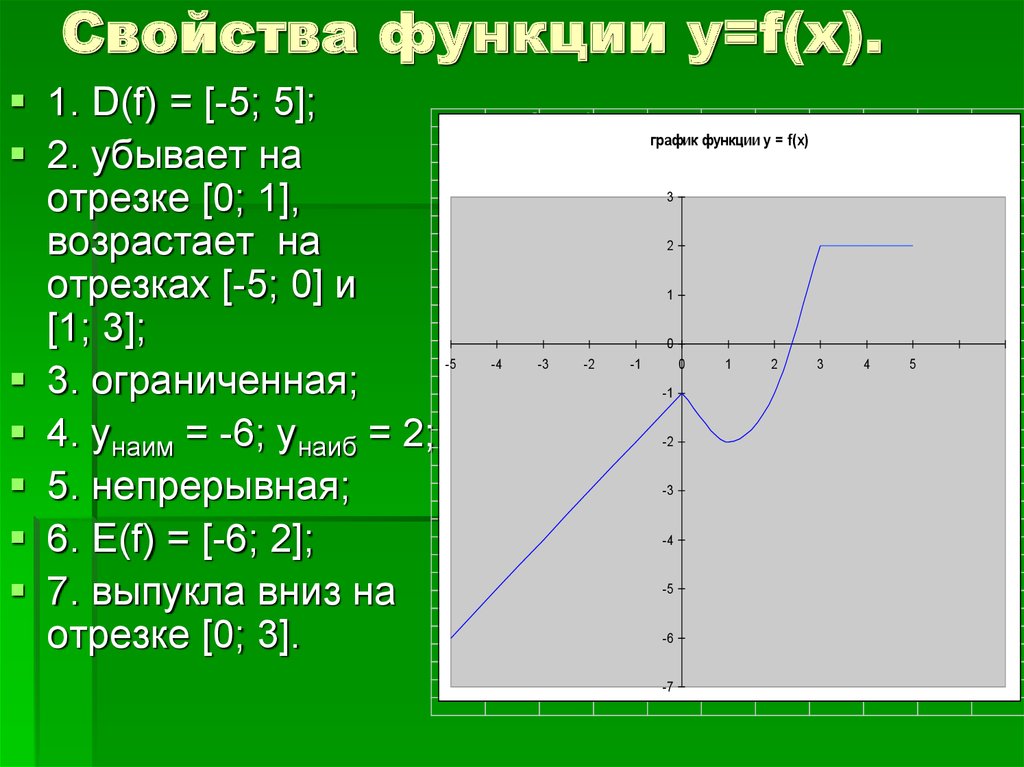
2. Свойства функции y=f(x).
1. D(f) = [-5; 5];2. убывает на
отрезке [0; 1],
возрастает на
отрезках [-5; 0] и
[1; 3];
3. ограниченная;
4. унаим = -6; унаиб = 2;
5. непрерывная;
6. Е(f) = [-6; 2];
7. выпукла вниз на
отрезке [0; 3].
-5
-4
-3
-2
-1
0
1
2
3
4
5
-6
-5
-4
-3
-2
-1
график функции y = f(x)
-1
-2
-1
2
3
2
2
2
2
1
0
-5
-4
-3
-2
-1
0
-1
-2
-3
-4
-5
-6
-7
1
2
3
4
5
3. Исследуйте
на монотонность функциюУ = х3 + 3х ;
на ограниченность функцию
У = √(25 – х2 ).
4. Тема урока «Свойства функций».
Цели урока:- изучить свойства монотонности и
ограниченности функций;
- научить исследовать функцию на
монотонность, ограниченность снизу,
сверху;
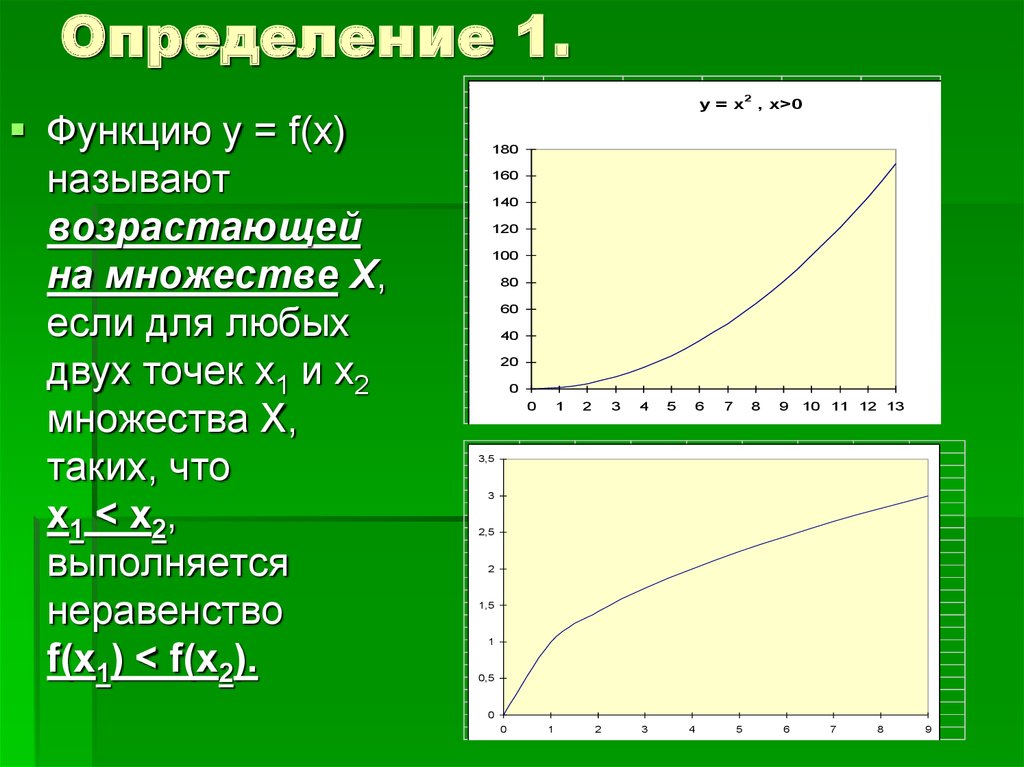
5. Определение 1.
xФункцию у = f(x)
называют
возрастающей
на множестве Х,
если для любых
двух точек х1 и х2
множества Х,
таких, что
х 1 < х 2,
выполняется
неравенство
f(x1) < f(x2).
y
0
1
2
180 3
4
160 5
6
140
7
120 8
9
100 10
11
80
12
60 13
0
1
4
9
16
25
36
49
64
81
100
121
144
169
y = x2 , x>0
40
20
0
0
1
2
x
3
4
5
6
7
8
9
10 11 12 13
y
0
1
2
3
4
5
6
7
8
9
3,5
3
2,5
2
0
1
1,414214
1,732051
2
2,236068
2,44949
2,645751
2,828427
3
1,5
1
0,5
0
0
1
2
3
4
5
6
7
8
9
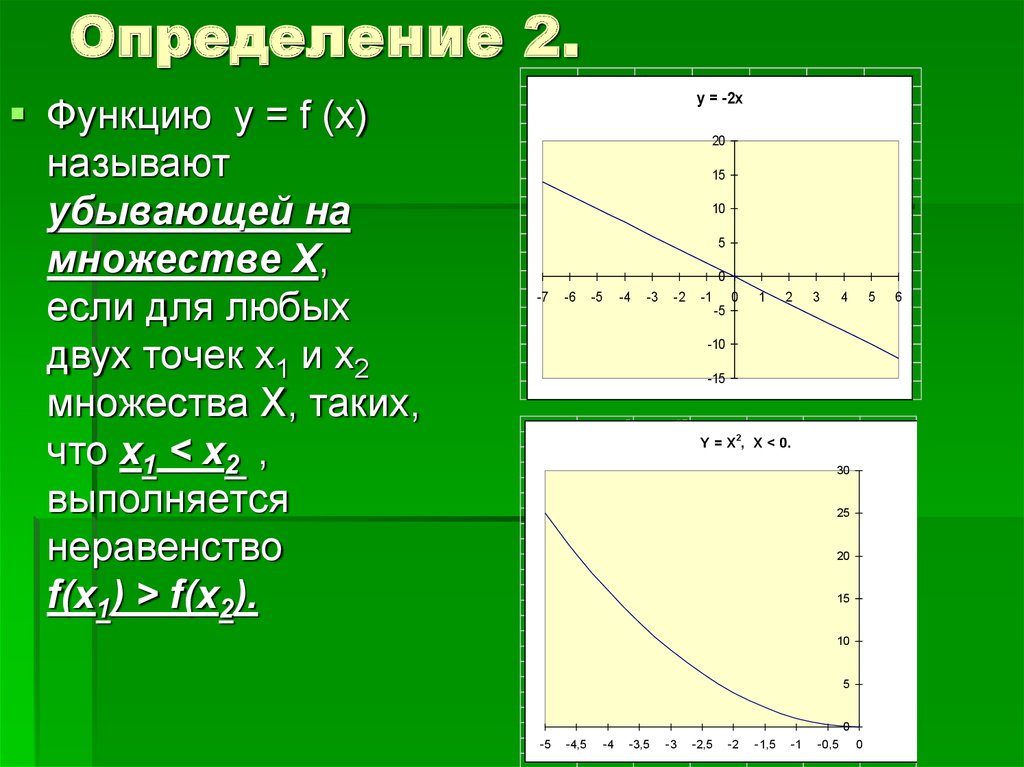
6. Определение 2.
xФункцию у = f (x)
называют
убывающей на
множестве Х,
если для любых
двух точек х1 и х2
множества Х, таких,
что х1 < х2 ,
выполняется
неравенство
f(x1) > f(x2).
-7
-6
y
-7
-6
-5
-4
-3
-2
-1
0
1
2
3
-44 -3
5
6
-5
14 y = -2x
12
10
20
8
6
15
4
2
10
0
5
-2
-4
0
-6
-2-8 -1 0
-5
-10
-12
-10
1
2
3
4
5
-15
-5
-4,5
-4
-3,5
-3
-2,5
-2
-1,5
-1
-0,5
0
0,5
1
1,5
25
20,25
16
12,25
9
6,25
4
2,25
1
0,25
0
Y = X2, X < 0.
30
25
20
15
10
5
0
-5
-4,5
-4
-3,5
-3
-2,5
-2
-1,5
-1
-0,5
0
6
7. Определите характер монотонности функции у = х3 + 3х.
Пусть х1 < х2, тогдаХ13 < х23,
3х1 < 3х2,
Х13 +3х1 < х23 +3х2.
3
Т.е. f(x1) < f(x2). Следовательно функция у = x +3x
возрастает на всей числовой прямой.
8.
3ГРАФИК ФУНКЦИИ Y=X -3X
1500
1000
500
0
-10 -9
-8
-7
-6
-5
-4
-3
-2
-1
-500
-1000
-1500
0
1
2
3
4
5
6
7
8
9
10
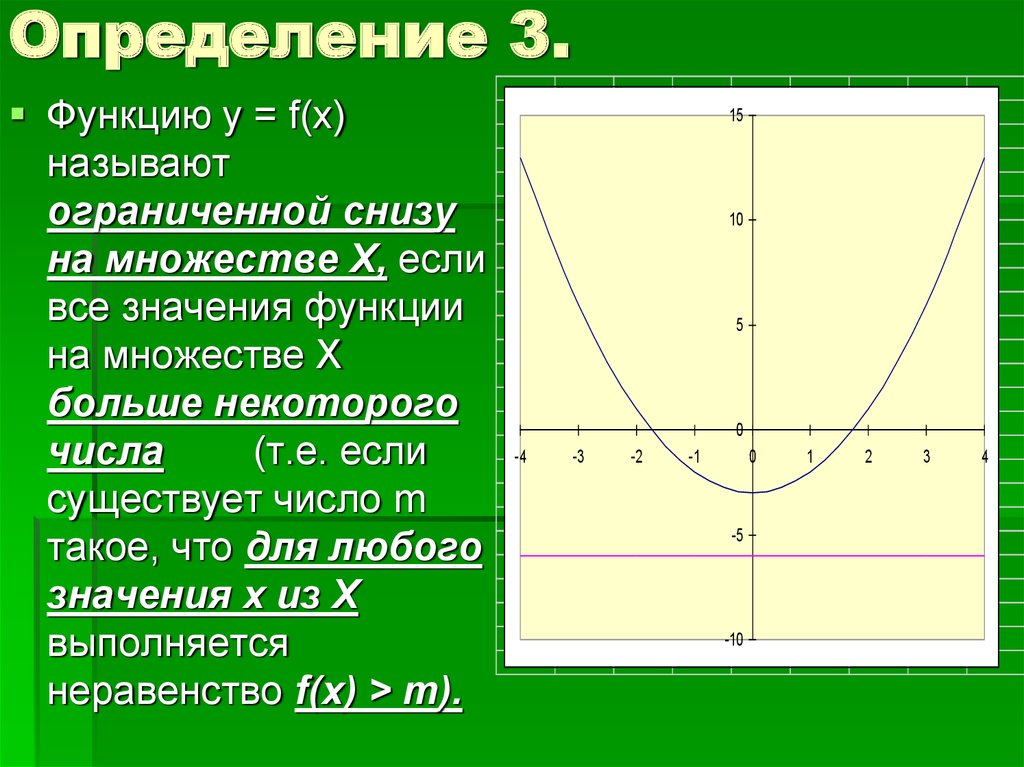
9. Определение 3.
Функцию у = f(x)называют
ограниченной снизу
на множестве Х, если
все значения функции
на множестве Х
больше некоторого
числа
(т.е. если
существует число m
такое, что для любого
значения х из Х
выполняется
неравенство f(x) > m).
y
x
-615
-6
-6
-6
-6
10
-6
-6
-6
-6
5
13
6
1
-2
-3
-2
1
6
13
-4
-3
-2
-1
0
1
2
3
4
0
-4
-3
-2
0
-1
-5
-10
1
2
3
4
10. Определение 4.
Функцию у = f(x)называют
ограниченной сверху
на множестве Х, если
все значения функции
меньше некоторого
числа
(т.е. существует
такое число М, что для
любого значения х из
множества Х
выполняется
неравенство f(x) <М).
-4
-3
-2
-1
0
1
2
3
4
-4
-3
-13
-6
-1
2
3
2
-1
-6
-13
-2
5
5
5
5
5
5
5
5
5
6
4
2
0
-1
0
-2
-4
-6
-8
-10
-12
-14
1
2
3
4
11. Исследуйте функцию у = √(25 – х2) на ограниченность.
1. √(25 – х2) ≥ 0, т.е. ф - ия ограниченаснизу.
2. х2 ≥ 0,
-х 2 ≤ 0,
25 – х2 ≤ 25,
√(25 – х2) ≤ 5, т.е. ф – ия ограничена сверху.
Следовательно 0 ≤ √(25 – х2) ≤ 5, т.е. функция
ограниченная.
12. Y = √(25 – x2)
-5-4,5
-4
-3,5
-3
-2,5
-2
-1,5
-1
-0,5
0
0,5
1
1,5
2
2,5
3
3,5
4
4,5
5
0
2,179449
3
3,570714
4
4,330127
4,582576
4,769696
4,898979
4,974937
5
4,974937
4,898979
4,769696
4,582576
4,330127
4
3,570714
3
2,179449
0
6
5
4
3
2
1
0
-5 -4,5 -4 -3,5 -3 -2,5 -2 -1,5 -1 -0,5
0
0,5
1
1,5
2
2,5
3
3,5
4
4,5
5
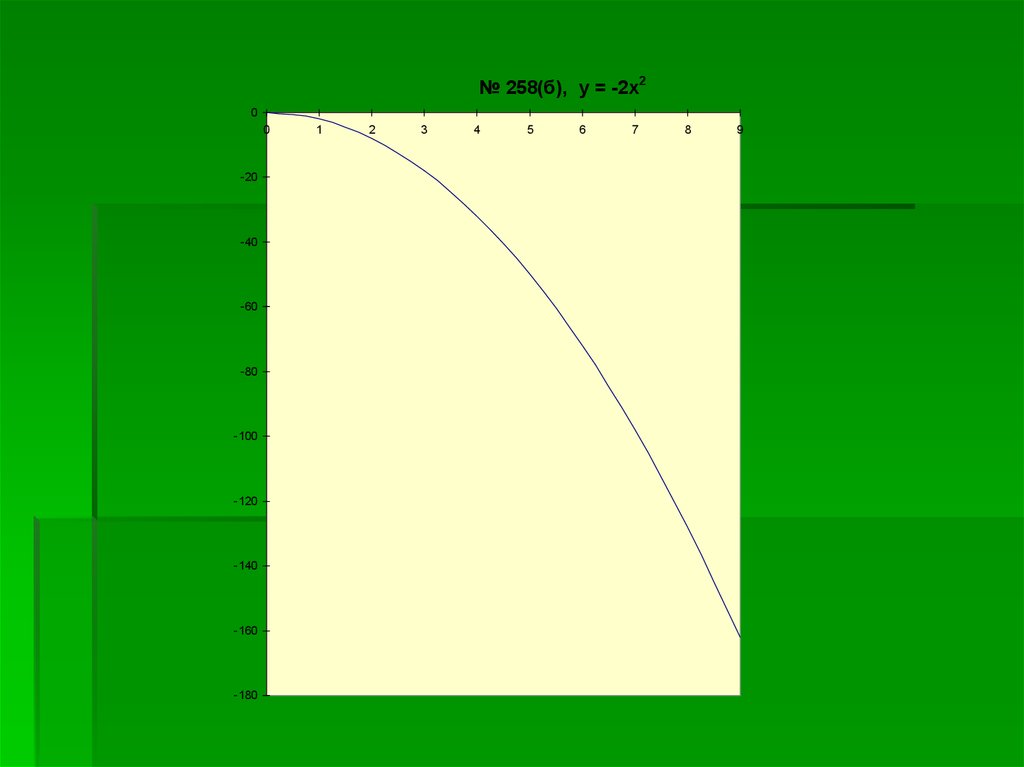
13.
№ 258(б), у = -2х20
0
-20
-40
-60
-80
-100
-120
-140
-160
-180
1
2
3
4
5
6
7
8
9
14.
№ 259(б), у = - 3х +135
30
25
20
15
10
5
0
-10
-9
-8
-7
-6
-5
-4
-3
-2
-1
0
15.
№259(г), у = - 2х + 56
4
2
0
0
-2
-4
-6
1
2
3
4
5
16. Домашнее задание
§9 (стр. 76-78);№ 253(г) и 257(г),
259(а) и 261(а);
Изобразить график функции:
Е(f)=[-3; 10],
D(f)=[-4; 6],
возрастает на промежутке [-4; 0],
убывает на промежутке [0; 6].











 Математика
Математика








