Функции и графики

1. Функции и графики

Драгунова Е. Ю. учитель математики
МОУ СОШ № 10 г.о. Жуковский
Функции и графики
Методическая разработка
к учебнику Ю. Макарычева
«Алгебра – 8» углубленное изучение

2. Функция, область определения и область значений функции.

Х
f
У
Х
f
У
f
f- функция
х соответствует
единственный у
Каждому
f- не функция
-Не каждому
х
- не единственный у

3.

Функцией (функциональной зависимостью)
называется зависимость переменной у от
переменной х, при которой каждому значению
х соответствует единственное значение у.
х
f
у
или
у =f(х)
Переменная х- независимая – аргумент.
Переменная у – зависимая – значение
функции( функция)

4. Свойства функции

Все значения, которые может принимать
аргумент (независимая переменная) образуют
область определения функции.
D (f)
Все значения, которые может принимать
функция (зависимая переменная) образуют
область (множество) значений функции.
E (f)

5. Свойства функции

Значения аргумента, при которых
функция обращается в нуль,
называются нулями функции
Промежутки, в которых функция
принимает только положительные или
только отрицательные значения,
называются промежутками
знакопостоянства функции

6.

у
9
8
7
6
5
4
3
2
1
-7 -6 -5 -4 -3 -2
-1
о
( ; 2) (3; )
( 2; 3)
-1
-2
1
-3
-4
-5
-6
2
3 4
5
6
7
х
у = 0 при х = -2
и х=3

7. Повторение.

№1.Какие
из данных графиков являются
Повторение.
графиками каких-либо функций?

8.

9.

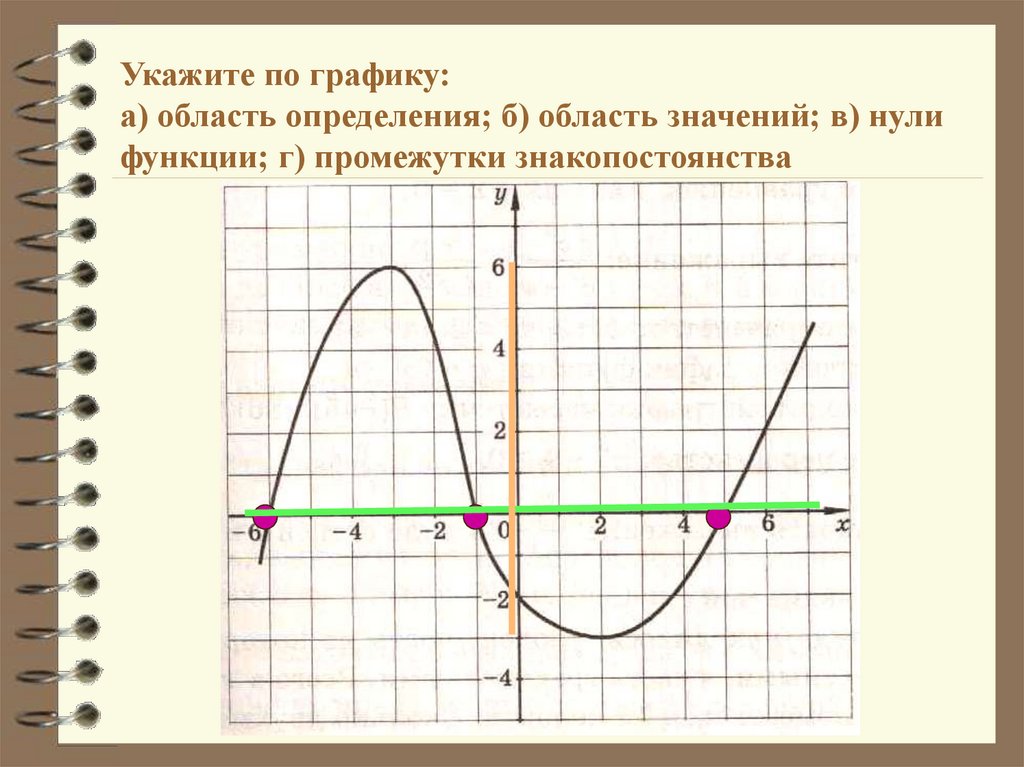
10. Укажите по графику: а) область определения; б) область значений; в) нули функции; г) промежутки знакопостоянства

11.

у=f(x) – данная функция (уравнение с двумя
переменными)
Пара (х0;f(х0)) – решение уравнения и
одновременно точка на координатной
плоскости.
Графиком функции называется множество
точек координатной плоскости, абсциссы
которых равны значениям аргумента, а
ординаты – соответствующим значениям
функции.

12. y = f(x)

у = -f(x)
y = f(-x)
у = f(x) - 1 у = 2f(x)
y = f(x-1)
y = f(3x)
x = f(y)

13. Построение графика функции с помощью геометрических преобразований

Растяжение и сжатие
Дано :
y=f(x)
Построить:
y = kf(x), к = 0
Берем х из области
определения
Берем х из области
определения
Вычисляем у =f(x)
Вычисляем у1= f(x), а
затем у = к f(х)

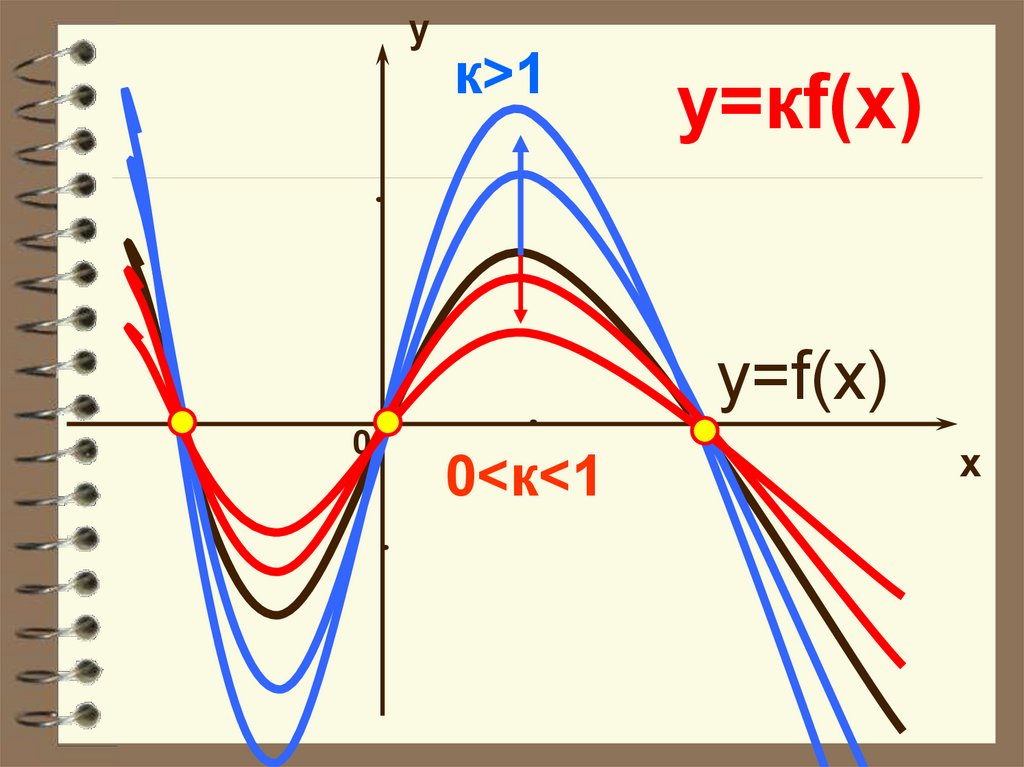
14.

y
к>1
y=кf(x)
y=f(x)
0
0<к<1
x

15.

y
y=f(x)
0
x
y=-f(x)

16.

для построения графика у = -к f(х)
Сначала сжатие или растяжение
Затем симметрия

17. Параллельный перенос графика

Дано :
y=f(x)
Берем х из области
определения
Вычисляем у =f(x)
Построить:
y = f(x)+n
Берем х из области
определения
Вычисляем у1= f(x), а
затем
у = f(х)+n
При одинаковых значениях х , у отличаются
на одно и тоже число.
График «сдвигается» вдоль оси у на n единичных
отрезков

18.

y
n>0
y=f(x)
0
x
n<0
y=f(x)+n

19. Параллельный перенос графика

Дано :
y=f(x)
Берем х из области
определения
Построить:
y = f(x-m)
Берем х из области
определения, затем
вычисляем (х-m)
Вычисляем у =f(x)
Вычисляем у = f(х-m)
При одинаковых значениях у , х отличаются
на одно и тоже число.
График «сдвигается» вдоль оси х на m единичных
отрезков

20.

y
y=f(x - m) y=f(x)
m<0
0
x
m>0

21.

Для построения графика у = f(x-m)+n
Сначала параллельный перенос вдоль
оси Х
Затем параллельный перенос вдоль оси У