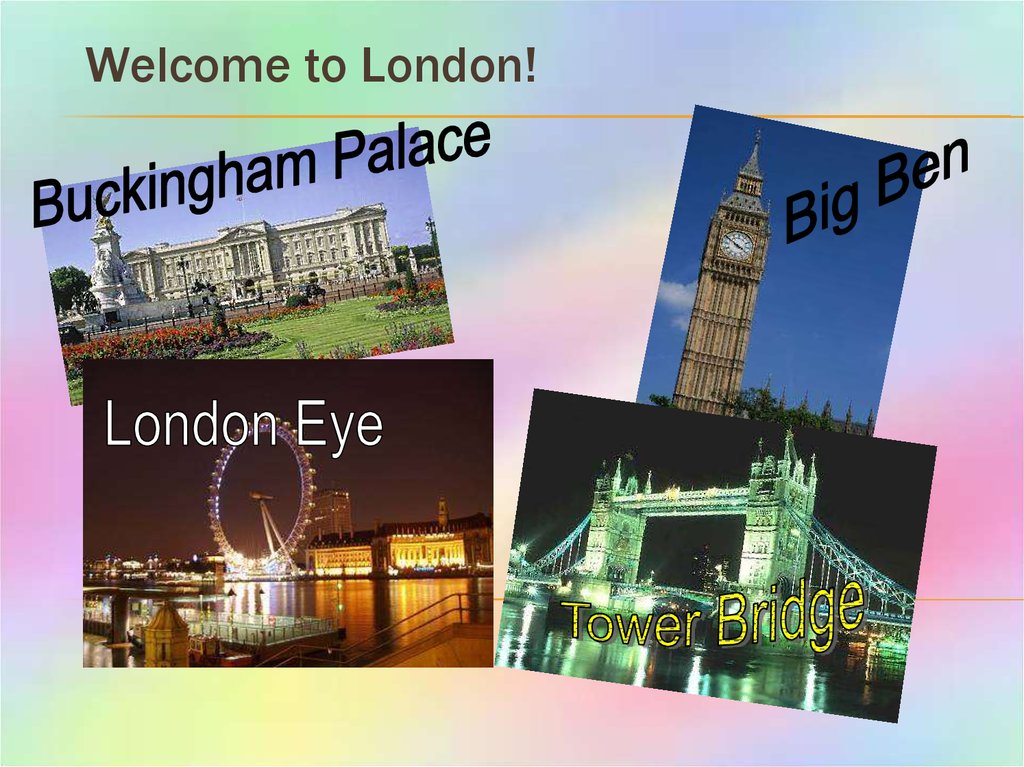
Welcome to London!

1.

Project presentation on the topic:
“Welcome to London!”

2. Welcome to London!

3.

The motto of our presentation is:
“ Learn English
and you’ll be lucky!”

4.

TRAFALGAR SQUARE

5.

Trafalgar Square

6.

Admiral Nelson’s
Column

7. The National Gallery

8.

St. Paul’s Cathedral

9.

BUCKINGHAM PALACE

10.

11.

12.

This is Buckingham Palace – the place where
British kings and queens live when they are in
London.
Important visitors often go to the palace. They meet
Queen Elizabeth and the royal family inside the
palace.
A lot of tourists go to Buckingham Palace.
They stand outside and see the Changing of the
Guard. It happens every day at 11.30 a.m.

13. The Houses of Parliament

14.

WESTMINSTER ABBEY

15.

Westminster Abbey is a symbol of
England. It’s a royal church. The legend
says that Westminster Abbey was
founded by St Peter himself. We know
that Westminster Abbey was built by
King Edward in 1065. The coronation of
all British Kings and Queens takes place
in Westminster Abbey.Some famous
English people are also buried here. Here
you can see the tombs of many British
kings and queens and other famous
people.

16.

TOWER OF LONDON

17.

18.

The Tower of London is a very old building. It
is nine hundred years old. In the early days of
England the English kings lived in the Tower.
Then it was a prison where many people died.
Black ravens had much food near the walls оf
the Tower in those days. Black ravens live
outside the Tower now. The English people like
them very much. Now it’s a museum housing
the National Collection of Armour and Royal
Regalia. Many tourists from other countries
come to see it. They see the dark stone halls
with small windows and thick doors. The
Tower is still guarded by the famous
Beefeaters who wear a traditional Sixteenth
century uniform.

19.

TOWER BRIDGE

20.

21.

22.

Piccadilly Circus is a square in
the central part of London. In the
square you can see people of
many nationalities. Piccadilly
Circus is the meeting-point of 6
streets. London’s famous
restaurants and best- known
theatres and cinemas are on
Piccadilly Circus .

23. Hyde Park

24. Hyde Park

25.

26.

Tourists in London always want to
visit Westminster and see Big Ben. They
want to see the clock in its tower and to
hear the bells. Big Ben is one of the most
famous clocks in the world. Big Ben is really
a bell. You hear it every hour. It is a big bell.
It weighs 13,720 kilograms.
It has a deep tone and you can hear it on the
radio: “This is the BBC. The time is six
o’clock.” And then you hear the deep boom of
Big Ben six times.

27. Madame Tussaud’s

28. The Sherlock Holmes Museum

29. Tate Gallery

30. The Globe Theatre

31.

32. Windsor Castle

33.

London streets

34.

DOUBLE DACKER BUS

35.

VICTORIA MEMORIAL

36. The Beatles

37. Game “Sights in London”

Which sights of London are visited by thousands. But
it’s official home for only one family.
It was a fortress, a royal palace and later a prison. It’s
a museum now.
Which of these sights is the best place for relax and
fun.
It’s London’s most famous bridge. It’s the last bridge
crossing the Thames.
It’s one of the most famous clocks in the world. You
can hear the sound of it every hour in London.

38.

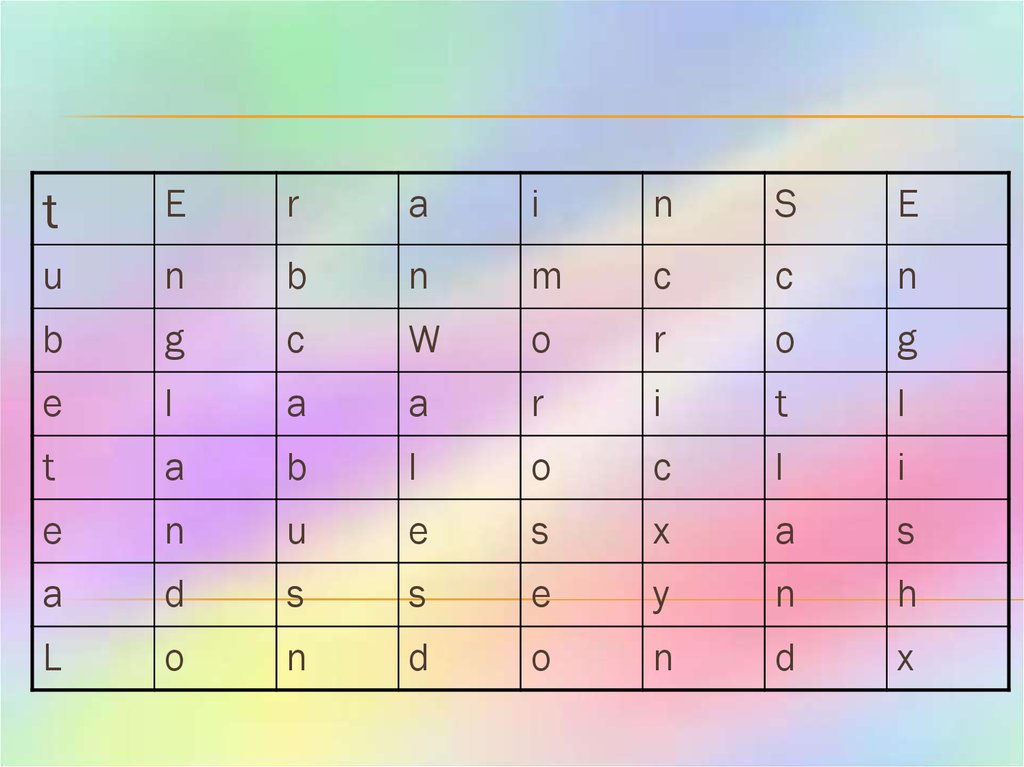
t
E
r
a
i
n
S
E
u
n
b
n
m
c
c
n
b
g
c
W
o
r
o
g
e
l
a
a
r
i
t
l
t
a
b
l
o
c
l
i
e
n
u
e
s
x
a
s
a
d
s
s
e
y
n
h
L
o
n
d
o
n
d
x

39.

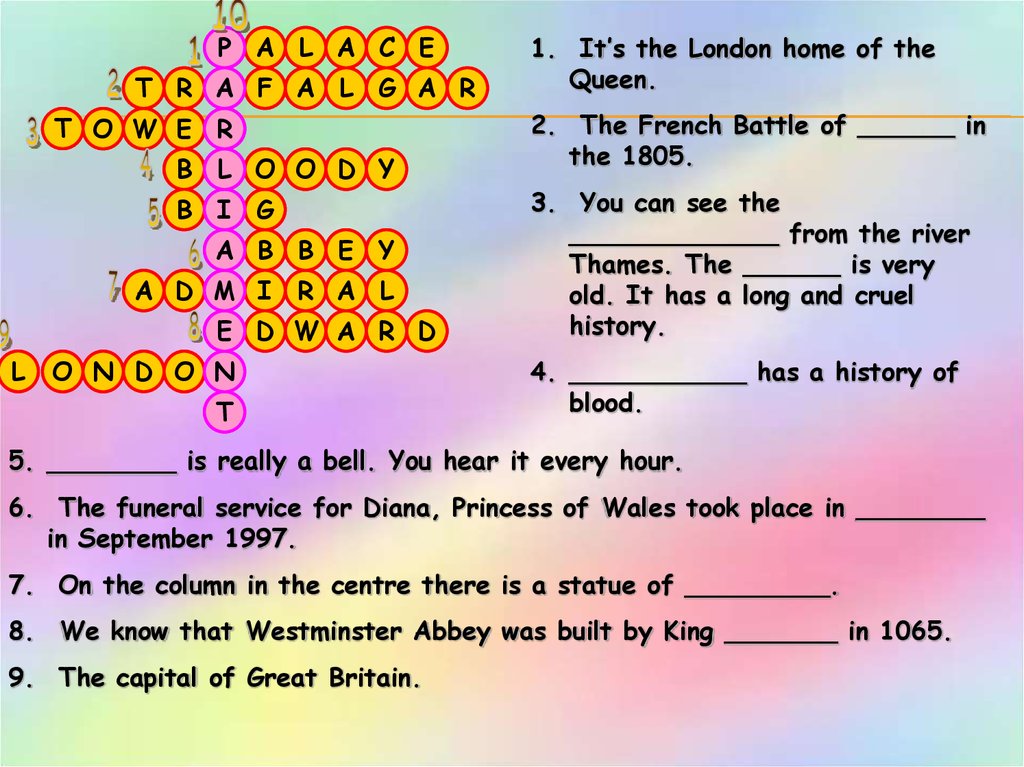
1. It’s the London home of the
Queen.
2. The French Battle of ______ in
the 1805.
3. You can see the
_____________ from the river
Thames. The ______ is very
old. It has a long and cruel
history.
4. ___________ has a history of
blood.
5. ________ is really a bell. You hear it every hour.
6. The funeral service for Diana, Princess of Wales took place in ________
in September 1997.
7. On the column in the centre there is a statue of _________.
8. We know that Westminster Abbey was built by King _______ in 1065.
9. The capital of Great Britain.

40.

P A L A C E
T R A F A L G A R
T O W E R
B L O O D Y
B I G
A B B E Y
A D M I R A L
E D W A R D
L
O N D O N
T
1. It’s the London home of the
Queen.
2. The French Battle of ______ in
the 1805.
3. You can see the
_____________ from the river
Thames. The ______ is very
old. It has a long and cruel
history.
4. ___________ has a history of
blood.
5. ________ is really a bell. You hear it every hour.
6. The funeral service for Diana, Princess of Wales took place in ________
in September 1997.
7. On the column in the centre there is a statue of _________.
8. We know that Westminster Abbey was built by King _______ in 1065.
9. The capital of Great Britain.

41.

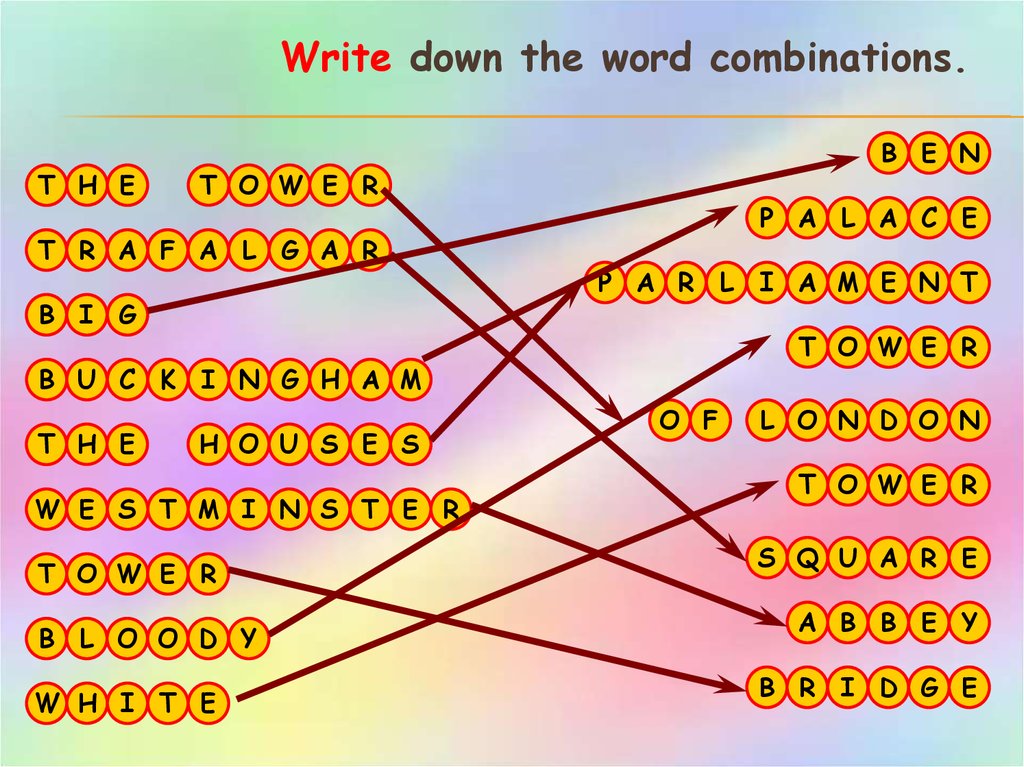
Write down the word combinations.
T H E
T O W E R
T R A F A L G A R
B I G
B U C K
T H E
B E N
P A L A C E
P A R L
T O W E R
I N G H A M
H O U S E S
W E S T M I N S T E R
T O W E R
B L O O D Y
W H I T E
I A M E N T
O F
L O N D O N
T O W E R
S Q U A R E
A B B E Y
B R I D G E

42.

Write down the word combinations.
T H E
T O W E R
T R A F A L G A R
B I G
B U C K
T H E
B E N
P A L A C E
P A R L
T O W E R
I N G H A M
H O U S E S
W E S T M I N S T E R
T O W E R
B L O O D Y
W H I T E
I A M E N T
O F
L O N D O N
T O W E R
S Q U A R E
A B B E Y
B R I D G E

43. English Queen

44. Queen Elizabeth the Second

45.

Her
Majesty
the Queen
Elisabeth II

46. Complete the sentences.

1. London stands on the river
а)
b)
c)
Nile
Mississippi
Thames
2. The population of London is
a)
Million people
b)
10 million people
c)
8 million people
3. The Queen of England lives in
a)
Buckingham Palace
b)
Westminster Abbey
c)
The Tower of London
4. Big Ben is
A palace
A square
A bell
5. The famous museum of waxworks
is called
Pushkin Museum
Madame Tussaud’s
The National Gallery

47. BRITAIN QUIZ

48. Choose the correct answer for each question.

1. What is the capital of Great
Britain?
a.
b.
c.
Edinburgh;
Boston;
London.

49.

Choose the correct answer for
question.
2.The British flag is often
called…
a. the Union Jack;
b. the Stars and Stripes;
c. the Maple Leaf.
each

50.

Choose the correct answer for
question.
each
3. What colour are the buses in
London?
a.
b.
c.
red;
blue;
black.

51.

Choose the correct answer for
question.
each
4. Britain's national drink is…
a. Tea;
b. Coca-Cola;
c. Coffee.

52.

Choose the correct answer for
question.
5.The kilt is…
a.
b.
c.
a pair of trousers;
a shirt.
a skirt;
each

53. 6. What is the official name of this country?

a) Britain
b) The United
Kingdom of Great
Britain
c) England

54. 7.What is the national flag of the UK?

1
6
2
5
3
4

55. 8.Money in the UK is…

a) Dollars
b) Pounds
c) Euro

56. 9.What is the most popular free time activity?

a) Watching TV
b) Gardening
c) Reading

57. 10.Which is the oldest university?

a) Cambridge
b) Oxford
c) London

58. 11.The British Prime Minister lives at…

a) 12 Whitehall
b) 10 Downing Street
c) 7 Russel Street
d) 15 Oxford Street

59. 12.The Great Fire of London broke out in…

a) 1066
b) 1766
c) 1106
d) 1666

60. 13.Sir Christopher Wren built…

a) Buckingham Palace
b) The Tower of London
c) Trafalgar Square
d) St. Paul’s Cathedral

61. 14.Speaker’s Corner is in…

a) Hyde Park
b) Green Park
c) Regent’s Park

62. 15.This is …

a) Westminster Abbey
b) The Houses of Parliament
c) The Tower

63. 16.When is Halloween celebrated?

a) December 25th
b) February 14th
c) October 31th

64. 17.In Scotland, what vegetable was traditionally carved into a jack-o’-lantern?

a) A watermelon
b) A turnip
c) A pumpkin

65. 18.You can see the column with a statue of Nelson in…

A) Piccadilly Circus.
B) Hyde Park.
C) Trafalgar Square.

66. 19. … is a very democratic park.

A) Hyde Park.
B) Regent’s Park.
C) St. Jame’s Park.

67. 20. London Zoo is in…

A) Regent’s Park.
B) St. Jame’s Park.
C) Hyde Park.

68. 21. They change the Guard every day at…

A) 9: 30 a.m.
B) 11: 30 a.m.
C) 12: 00 a.m.

69. 22. Piccadilly Circus is the meeting-point of …

A) 5 streets.
B) 7 streets.
C) 6 streets.

70. 23.The seat of the British government is…

A) the Houses of Parliament.
B) Buckingham Palace.
C) Piccadilly Circus.

71.

1. The capital of Britain.
2.The name of the queen of Britain.
3.The symbol of England.
4.The country that consists of England, Scotland and
Wales.
5.One of the colours of the flag of Britain.
6.The language that the English speak.
7.The favourite English domestic animal.
8.The weather in Britain.
9.The widest river in Britain.

72.

73.

74.

75.

76.

77.

78. Do you like it or not?

79.

Good
bye and good luck !!!