Похожие презентации:
Основы теории ошибок измерений
1. ОСНОВЫ ТЕОРИИ ОШИБОК ИЗМЕРЕНИЙ
Виды измерений и погрешностейИзмерением какой-либо физической
величины называется операция, в результате
которой мы узнаем, во сколько раз
измеряемая величина больше (или меньше)
соответствующей величины, принятой за
единицу
2.
Виды измерений классифицируются:– по способу получения результата (прямые и
косвенные);
– по методу измерений (абсолютные,
относительные и пороговые);
– по условиям измерений (равноточные,
неравноточные);
– по степени достаточности измерений
(необходимые, избыточные)
3.
При прямых измерениях измеряетсянепосредственно исследуемая величина
При косвенных измерениях исследуемая
величина измеряется как функция по
результатам измерения других величин
Например, ускорение автомобиля при
разгоне определяется по результатам
измерения расстояния и времени разгона;
вычисление плотности – по массе и объему
4.
Абсолютные измерения – это прямыеизмерения в единицах измеряемой величины
Относительные измерения
представляют собой отношения измеряемой
величины к величине играющей роль единицы
или к величине, принимаемой за исходную
При пороговых измерениях фиксируется
только факт нахождения величины в
одностороннем или двухстороннем допуске
(по принципу "да/нет")
5.
Равноточные измерения проводятся водинаковых условиях одними и теми же
измерительными приборами и с одинаковой
степенью тщательности.
При этом в ряду измерений нельзя отдать
предпочтение какому-либо одному или
нескольким значениям
Неравноточные измерения не отвечают
указанным выше требованиям
6.
Избыточные измерения имеют посравнению с необходимыми большее число
измерений либо большую точность, содержат
среди измерений зависимые, т. е. дают
избыточную информацию
Надежность результатов исследования в
значительной степени зависит от точности
измерений
Под точностью измерений понимают
степень соответствия результата
измерения действительному значению
измеряемой величины
7.
Снять показания с прибора – не значит толькоизмерить. Необходимо еще оценить ошибки
(погрешности) измерений
Погрешность измерения – это отклонение
результата измерения от истинного значения
измеряемой величины
8.
Под истинным значением измеряемойвеличины принято считать
– среднюю арифметическую величину ряда
измерений;
– известное эталонное значение;
– величину, полученную в результате более
точных (не менее чем на порядок) измерений
9.
Основные источники ошибокПервый источник заключен в датчике,
который неправильно реагирует на
измеряемую величину.
Например, если тензосопротивление плохо
наклеено на упругий элемент, то деформация
его решетки не будет соответствовать
деформации упругого элемента
Второй источник – измерительное
устройство, в котором возможны погрешности
из-за неправильного функционирования его
механических или электрических элементов
10.
Третий источник – сам наблюдатель,который из-за неопытности или усталости
неправильно считывает показания прибора
Ошибки могут возникнуть из-за влияния
измерительного устройства на объект
измерения (например, при разрушающем
методе контроля), влияния окружающей среды
(температура, загазованность и т. п.),
методических погрешностей, допущенных
экспериментатором
11.
Эти источники ошибок приводят к появлениютрех типов ошибок: случайных,
систематических и грубых
Случайная погрешность – это погрешность,
которая в отдельных измерениях может
принимать случайные, заранее конкретно
неизвестные значения.
Случайные погрешности обязаны своим
происхождением ряду как объективных, так и
субъективных факторов, действие которых
неодинаково в каждом опыте и не может быть
учтено.
12.
Случайные погрешности различаются вотдельных измерениях, сделанных в одинаковых
условиях одними и теми же измерительными
приборами. Исключить случайные погрешности
нельзя. Можно только оценить их значение
Случайные погрешности определяются по
законам теории ошибок, основанной на теории
вероятностей
13.
Систематическая погрешность – этопогрешность, вызванная факторами,
действующими одинаковым образом при
многократном повторении одних и тех же
измерений с помощью одних и тех же
измерительных приборов
В качестве примера систематической ошибки
рассмотрим случай взвешивания на чашечных
весах с помощью неточных гирь. Если взятая
нами гиря имеет ошибку, скажем 0,1 г, то вес
тела (пусть 1000 г) будет завышенным (или
заниженным) на эту величину, и чтобы
получить верное значение, необходимо учесть
эту ошибку, прибавив к полученному весу (или
вычтя из него) 0,1 г, P=(1000±0,1) г
14.
Грубая погрешность или промахвызывается просчетом экспериментатора или
неисправностью средств измерения, или резко
изменившимися внешними условиями
Грубые погрешности приводят к явному
искажению результата, поэтому их надо
исключить из общего числа измерений
15.
По форме числового представленияпогрешности делятся на абсолютные и
относительные
Абсолютная погрешность – это
разность между результатом измерения и
его истинным значением: x x a
где x – результат измерения; a – истинное
значение
Относительная погрешность – это
погрешность, приходящаяся на единицу
измеренной величины; обычно выражается в
x
процентах
a
100%.
16.
Случайные погрешности и ихраспределение
Чтобы выявить случайную погрешность
измерений, необходимо повторить измерение
несколько раз
Если каждое измерение дает заметные от
других результаты, мы имеем дело с ситуацией,
когда случайная погрешность играет
существенную роль
17.
Наиболее вероятным значением измеряемойвеличины из серии измерений является ее
среднее значение
Разброс измеряемой величины относительно
ее среднего значения определяется величиной
средней квадратической погрешности
отдельного измерения
18.
Пусть в эксперименте в результатенезависимых и равноточных измерений
постоянной величины а получены значения х1,
х2, …, хn
Абсолютные погрешности xi xi a
рассматривают как случайные величины
Независимость измерений понимается как
взаимная независимость случайных величин xi ,
а равноточность – как подчинение величин xi
одному и тому же закону распределения (кроме
того измерения сделаны одним и тем же методом
и с одинаковой степенью тщательности)
19.
аВ качестве оценки неизвестной величины
по данным измерений обычно берут среднее
арифметическое результатов измерений
1 n
x xi .
n i 1
n
2
(
x
a
)
i
2
Дисперсия отдельных измерений i 1
обычно неизвестна, и для ее оценки
n
используется величина
2
Sn
x
( xi x )
i 1
n 1
2
.
n 1
20.
Среднюю квадратическую (стандартную)погрешность (СКО) находятся по формуле
,
2
для ее оценки вычисляется величина
lim Sn .
Sn
2
Sn
n
Sn
100 %
Величина w
x
называется коэффициентом вариации
Обычно принимается, что погрешности
подчиняются нормальному закону распределения
случайных величин
21.
При этом предполагается:1) погрешности измерений могут принимать
непрерывный ряд значений;
2) при большом числе наблюдений погрешности
равных значений, но разных знаков встречаются
одинаково часто;
3) частота появления погрешностей
уменьшается с увеличением величин
погрешностей
22.
Эти предположения приводят к законураспределения погрешностей, описываемому
формулой Гаусса:
y
1
2
e
( x ) 2
2 2
.
Форма кривых Гаусса зависит от величин
Чем больше
.
, тем больше рассеивание
случайной погрешности
23.
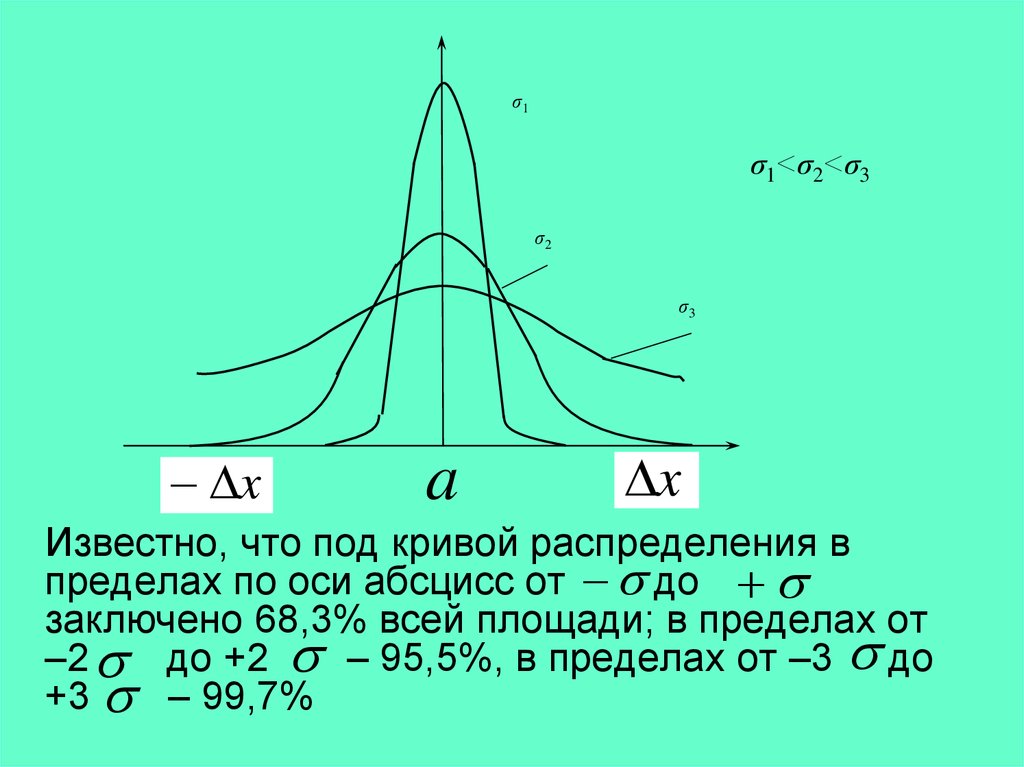
σ1σ1<σ2<σ3
σ2
σ3
x
a
x
Известно, что под кривой распределения в
пределах по оси абсцисс от до
заключено 68,3% всей площади; в пределах от
–2 до +2 – 95,5%, в пределах от –3 до
+3 – 99,7%
24.
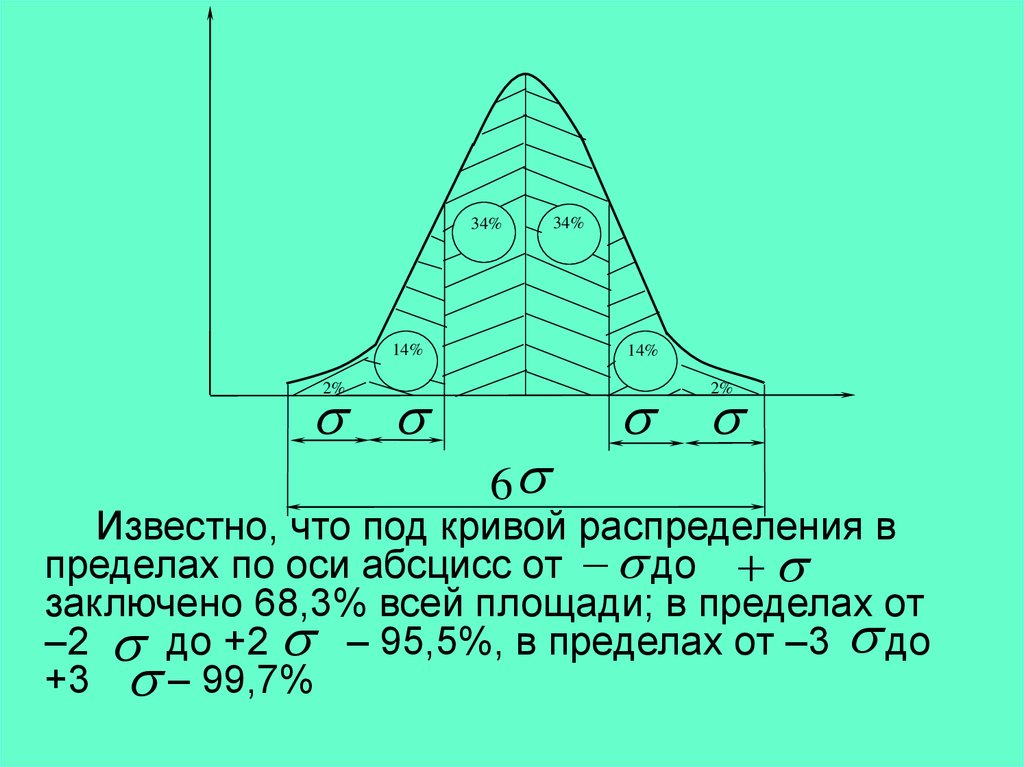
34%14%
34%
14%
2%
6
2%
Известно, что под кривой распределения в
пределах по оси абсцисс от до
заключено 68,3% всей площади; в пределах от
–2 до +2 – 95,5%, в пределах от –3 до
+3 – 99,7%
25.
Замечание. В ряде случаев экспериментальныеданные лучше описываются другими законами
распределения случайных величин, например,
законом Пуассона:
y
2 x 2
e
x!
.
26. Закон сложения случайных ошибок
Пусть измеряемая величина Z является суммой(или разностью) двух величин X и Y, результаты
измерений которых независимы.
Тогда можно доказать, что S Z S X S Y
2
если S X , S Y2 , S Z2 – дисперсии величин, или
2
SZ
2
SX
2
SY
2
2
27.
Если Z является суммой не двух, а большегочисла слагаемых, то закон сложения ошибок
будет таким же, т. е. средняя квадратичная
ошибка суммы или разности двух (или
нескольких) независимых величин равна корню
квадратному из суммы дисперсий отдельных
слагаемых
Для нахождения суммарной ошибки нужно
складывать не сами ошибки, а их квадраты
28.
Средняя квадратичная ошибка суммы илиразности двух (или нескольких) независимых
величин равна корню квадратному из суммы
дисперсий отдельных слагаемых
SZ
2
SX
2
SY
29. Выводы:
1. Необходимо учитывать роль каждой из ошибокв общей ошибке результата.
Значение отдельных ошибок очень быстро
падает по мере их уменьшения.
В первую очередь стоит уменьшать ошибку,
имеющую наибольшую величину
Относительная погрешность суммы
Sz
Z
S x2 S y2
X Y
30.
Пример: пусть X и Y – два слагаемых,определенных со средними квадратичными
ошибками S X и S Y , причем, известно, что S Y В
два раза меньше, чем S X . Тогда ошибка суммы
будет
Z X Y
2
SZ
2
SX
2
SY
2
SX
Sx 2 5 2
( ) SX .
2
4
S Z 1,1S X .
31.
2. Средняя квадратическая погрешностьсреднего арифметического равна средней
квадратической погрешности отдельного
результата, деленная на корень квадратный
Sn
из числа измерений: S x
,
n
S n – средняя квадратичная погрешность
отдельного измерения
32.
Пусть измеряемая величина Z являетсяразностью двух величин X и Y, результаты
измерений которых независимы.
Тогда ее относительная погрешность
Sz
Z
2
Sx
2
Sy
X Y
33.
Невозможно добиться хорошей точностиизмерений какой-либо величины, строя
измерения так, что она находится как
небольшая разность результатов независимых
измерений двух величин, существенно
превышающих искомую
34.
35.
36. Доверительный интервал и доверительная вероятность
1. Необходимо учитывать роль каждой из ошибокв общей ошибке результата.
Значение отдельных ошибок очень быстро
2
2
2
S
S
S
Тогда
можно
доказать,
что
падает по мере их уменьшения.
Z
X
Y
2
если S X , S Y2 , S Z2 – дисперсии величин, или
SZ
2
SX
2
SY
Средняя квадратичная ошибка суммы или
разности двух (или нескольких) независимых
величин равна корню квадратному из суммы
дисперсий отдельных слагаемых
37. Доверительный интервал и доверительная вероятность
1. Необходимо учитывать роль каждой из ошибок в общейошибке результата.
Значение отдельных ошибок очень быстро падает по мере
их уменьшения.
2
2
2
S
S
S
Тогда можно доказать, что
Z
X
Y
если S X2,
S Y2, S Z2
– дисперсии величин, или
SZ
2
SX
2
SY
Средняя квадратичная ошибка суммы или разности
двух (или нескольких) независимых величин равна корню
квадратному из суммы дисперсий отдельных слагаемых
38.
Количество опытов при ортогональном ЦКП определяется поформуле
n
N 2 2n 1
где 2n – количество опытов, образующих полный факторный
эксперимент; 2n – число так называемых «звездных» точек в
факторном пространстве, имеющих координаты (±α, 0, 0, ..., 0);
(0, ±α, 0, ..., 0), ..., (0, 0, ..., ±α). Здесь величина α называется
«звездным» плечом; 1 – опыт в центре планирования, т. е. в
точке факторного пространства с координатами (0, 0, ..., 0)
Значения «звездного» плеча α для ЦКП с различным числом
факторов n следующие:
n
α
2
1,000
3
1,215 1,414
4
5
1,547
Эти значения α выбраны из условия ортогональности
матрицы планирования
39.
40.
41. Закон сложения случайных ошибок
Если поверхность отклика не может быть описана многочленомвида
y b0 b1 X1 b2 X 2 bn X n b12 X1 X 2 b(n 1)n X n 1 X n
для адекватного математического описания используется
многочлен более высокой степени, например, отрезок ряда
Тейлора, содержащий члены с квадратами переменных. Тогда
используют центральное композиционное планирование (ЦКП)
эксперимента.
Различают два вида ЦКП:
ортогональное и
ротатабельное
42.
Количество опытов при ортогональном ЦКП определяется поформуле
n
N 2 2n 1
где 2n – количество опытов, образующих полный факторный
эксперимент; 2n – число так называемых «звездных» точек в
факторном пространстве, имеющих координаты (±α, 0, 0, ..., 0);
(0, ±α, 0, ..., 0), ..., (0, 0, ..., ±α). Здесь величина α называется
«звездным» плечом; 1 – опыт в центре планирования, т. е. в
точке факторного пространства с координатами (0, 0, ..., 0)
Значения «звездного» плеча α для ЦКП с различным числом
факторов n следующие:
n
α
2
1,000
3
1,215 1,414
4
5
1,547
Эти значения α выбраны из условия ортогональности
матрицы планирования
43.
Уравнение регрессии при ортогональном ЦКП ищут вследующем виде
y b0* b1 X 1 b2 X 2 ... bn X n b12 X 1 X 2 ... b( n 1) n X n 1 X n
b11 X 1* ... bnn X n*.
Переменные величины
X ji
X 2ji
1
N
N
X 2ji
j 1
здесь j – номер опыта; i – номер фактора, введены для того,
чтобы матрица планирования была ортогональна и
коэффициенты регрессии определялись независимо друг от
друга по результатам опытов. Чтобы получить уравнение
регрессии в обычной форме
y b0 b1 X 1 b2 X 2 ... bn X n b12 X 1 X 2 ... b( n 1) n X n 1 X n
b11 X 12 b22 X 22 ... bnn X n2 ,
b11 N 2
bnn N 2
находят величину b0 b
X ji ...
X jn .
N j 1
N j 1
*
0
44. Ортогональный план
Это план 2-ого порядка nпосле преобразований (*)2
xij
j 1
(*) x ij x ij 2
x ij 2 x i 2
n
Эти преобразования позволяют усреднить случайные
погрешности
Ортогональный план 2-ого порядка
Тогда уравнение регрессии
k
k
k
y b0 bi xi biu xi xu bii xi ;
j 1
i , u 1
i 1
В итоге уравнение регрессии преобразуется к виду
k
k
k
y b0 bi xi biu xi xu bii ( xi 2 xi 2 )
j 1
i , u 1
i 1
45.
Коэффициенты регрессии при ортогональном ЦКП считают последующим формулам
b0*
1
N
N
yj
j 1
N
N
X ji y j
bi
j 1
N
( X ji )
где i ≠ 0
bik
2
X ji X j k y j
j 1
N
( X ji X jk )
j 1
j 1
N
bii
j 1
N
X *ji y j
(X
j 1
*
ji
)
2
2
где i ≠ k
46.
Для расчета оценок дисперсий в определении коэфф-товS y2
регрессии используют следующие выражения 2
S S
2
b0
nS
2
b0*
Sb2i k N
bii
N
*
0
N
X ji
2
j 1
S
S
2
bi
где i ≠ k
2
2
y
(X
N
где i ≠ 0
N
j 1
S y2
( X ji X jk )
j 1
Sb
2
ji
)
2
S b2ii
S y2
N
(X
j 1
*
ji
)
2
Коэффициент bi, считается значимым, если bi Sb t , n .
i
Аналогично проверяется значимость остальных коэфф-тов
регрессии. Проверка адекватности уравнения регрессии
осуществляется с помощью критерия Фишера
2
S ад
Fр 2
Sвоспр
47. Метод ротатабельного центрального композиционного планирования
Метод ротатабельного планирования эксперимента позволяетполучать более точное математическое описание поверхности
отклика по сравнению с ортогональным ЦКП, что достигается
благодаря увеличению числа опытов в центре плана и
специальному выбору величины «звездного» плеча α.
Это план, у которого точки плана располагаются на
окружностях (сферах, гиперсферах)
Точность оценивания функции отклика по любому
направлению факторного пространства (для всех точек
плана) одинаковая, что позволяет наилучшим образом
извлечь максимальное количество (несмещенной)
информации из плана
48.
Ротабельный план 2-ого порядкаДля того, что бы привести план 2-ого порядка к
ротатабельному, величину плеча выбирают из условия
k
4
(**) 2 при k 5 и 2
k 1
4
при k 5
49.
При ротатабельном ЦКП для вычисления коэффициентоврегрессии и соответствующих оценок дисперсий находят
следующие константы
1
A
2 Β (n 2 )Β n
nN
Β
n 2 N N 0
C
N
N N0
где n – число факторов; N – общее число опытов
ротатабельного ЦКП; N0 – число опытов в центре плана
На основании результатов эксперимента вычисляют след.
N
N
суммы
S0 y j
Si X ji y j (где i=1,2,…,n),
j 1
j 1
N
Sik X ji X jk y j
j 1
N
(где i ≠ k),
Sii X 2ji y j
i 1
(где i=1,…, n)
50.
Формулы для расчета коэффициентов регрессии имеютследующий вид
n
2 AΒ
b0
S0 Β n 2 C Sii
N
i 1
CSi
bi
N
C 2 Sik
bik
BN
где i ≠ k
n
AC
bii
S iiC B n 2 n C 1 B Sii 2 BS0
N
i 1
51.
Оценки дисперсий в определении коэфф-тов регрессиивычисляют по следующим формулам
2 AB (n 2) 2
S
Sвоспр
b
N
2
C 2 Sвоспр
(где i≠k)
N
2
S
2
bi
S
0
2
воспр
(где i=1,2,…,n)
N N0
S2
bik
Sb2
ii
2
AC 2 Sвоспр
N
B n 1 n 1
Коэффициент bi, считается значимым, если bi Sb t , n .
i
Аналогично проверяется значимость остальных коэфф-тов
регрессии
52.
Оценку дисперсии адекватности рассчитывают по формулеN
(y
2
S ад
j 1
э
j
2
y jp ) 2 Sвоспр
( N 0 1)
(n 2)( n 1)
N
( N 0 1)
2
С ней связано число степеней свободы
f ад
(n 2)(n 1)
N
( N0 1)
2
Проверку адекватности уравнения регрессии осуществляют
с помощью критерия Фишера
2
S ад
Fр 2
Sвоспр
53.
Пример. Рассмотреть ротатабельное ЦКП для двух факторов.Матрица планирования и результаты эксперимента приведены в
таблице
Матрица планирования и результаты эксперимента
Система опытов
Номер
опыта
Полный
факторный
эксперимент
1
2
3
4
5
6
7
8
9
10
11
12
13
Опыты в
"звездных"
точках
Опыты в
центре плана
X1
1
+1
1
+1
+1,41
1,41
0
0
0
0
0
0
0
X2
1
1
+1
+1
0
0
+1,41
1,41
0
0
0
0
0
X3
+1
1
1
+1
0
0
0
0
0
0
0
0
0
X12
X 22
+1
+1
+1
+1
2
2
0
0
0
0
0
0
0
+1
+1
+1
+1
0
0
2
2
0
0
0
0
0
y эj
66,8
66,2
74,8
67,8
62,1
67,5
76,4
69,6
66,3
67,2
67,0
66,2
67,2
y jp
67,4
66,8
75,4
68,4
62,8
68,1
76,8
70,2
66,7
66,7
66,7
66,7
66,7
54.
Для нахождения коэффициентов регрессии вычислимследующие вспомогательные коэффициенты
13
1
2 13
1,63
0,5 C
B
0,81 A
8
2 0,81 2 2 0,81 2
(2 2)(13 5)
На основании результатов опытов вычислим вспомогательные
суммы
13
S0
j 1
y эj
885,1
13
13
S 2 X j 2 y эj 19,2
S1 X j1 y эj 15,2
j 1
j 1
13
S12 X j1 X j 2 y эj 6,4
j 1
13
S11 X 2j1 y эj 535,6
j 1
13
S 22 X 2j 2 y эj 567 ,6
j 1
Коэффициенты регрессии рассчитываем по формулам
55.
2 AB2 0,5 0,81
b0
[ S0 B(n 2) C ( S11 S22 )]
[885,1 0,81(2 2)
N
13
CS1 1,63( 15,2)
1,63(535,6 567,6)] 66,7;
b1
1,89
N
13
C 2 S12 (1,63)2 ( 6,4)
CS2 1,63 19,2
b2
2,41
b12
1,61
N
13
BN
0,81 13
AC
b11
{S11C[ B(n 2) n] C (1 B)( S11 S 22 ) 2 BS0 }
N
0,5 1,63
{535,6 1,63[0,81(2 2) 2] 1,63(1 0,81)(535,6 567 ,6)
13
2 0,81 885,1} 0,6;
AC
b22
{S 22C[ B(n 2) n] C (1 B)( S11 S 22 ) 2 BS0 }
N
0,5 1,63
{567 ,6 1,63[0,81(2 2) 2] 1,63(1 0,81)(535,6 567 ,6)
13
2 0,81 885,1} 3,4.
56.
Оценку дисперсии воспроизводимости можно найти наосновании результатов опытов, проведенных в центре плана
1
y
N0
N0
j 1
э 1
y j (66,3 67,2 67,0 66,2 67,2)
5
N
S
2
воспр
1
э
(
y
j y ) 0,3
N 0 1 j 1
67
0
Эта величина найдена при числе степеней свободы
f N0 1 5 1 4
Оценки дисперсий в определении коэфф. регрессии
2 AB (n 2) 2
2 0,5 0,81(2 2)0,3
S
Sвоспр
0,0748
N
13
2
2 2
Sy
C
S y (1,63)2 0,3
0,3
2
2
Sbi
0,0375
Sb
0,0613
N N0 13 5
ik
N
13
2
b0
Sb2ii
AC 2 S y2
N
0,5(1,63)2 0,3
[ B(n 1) (n 1)]
[0,81(2 1) (2 1)] 0,0438
13
57.
Пользуясь таблицей значений критерия Стьюдента, находимдля
f 4
и
P 0,95
t
,n
2,78
Sb t ,n 0,274 2,78 0,761
Sbi t , n 0,194 2,78 0,539
Sb t ,n 0,248 2,78 0,689
Sbii t , n 0,209 2,78 0,581
0
ik
Для проверки значимости коэффициентов регрессии рассмотрим соотнош.
b1 1,89 Sb t , n
b0 66 ,7 Sb t , n
0
i
b12 1,61 Sb t , n
b11 0,61 Sb t , n
ik
ii
b2 2,41 Sb t , n
i
b22 3,4 Sb t ,n
ii
Все коэффициенты регрессии значимы. Вычисляем оценку дисперсии
адекватности
N
(y
э
j
2
y jp ) 2 Sвоспр
( N 0 1)
3,81 0,3 4
S
0,87
(n 2)( n 1)
4 3
N
( N 0 1) 13
4
2
2
2
ад
j 1
58.
Число степеней свободы, связанных с этой оценкой дисперсииf ад N
(n 2)(n 1)
4 3
( N 0 1) 13
4 3
2
2
Расчетное значение критерия Фишера
2
S ад
0,87
F 2
2,9
S воспр 0,3
Из таблицы значений критерия Фишера соответствующее значение
критерия FT 6,6 . Условие Fp F выполнено, следовательно,
T
уравнение регрессии
y 66,7 1,89 X 1 2,41X 2 1,61X 1 X 2 0,61X 12 3,40 X 22
адекватно представленным результатам эксперимента
Перейдем в уравнение регрессии от кодированных переменных к физическим
Пусть в нашем примере кодированные переменные X1 и X2 представляют
собой температуру и концентрацию, причем координаты центра плана
x01= 60°С и x02= 30%, а шаги варьирования Δx1= 5°С и Δх2= 1% . Тогда
x x
X1 1 01 0,2 x1 12
x1
x2 x02
X2
x2 30
x2
59.
Подставляя их в полученноепреобразуем его к виду
в этом примере уравнение регрессии,
y 2409 9,57 x1 19,7 x2 0,32 x1 x2 0,0244 x12 3,4 x22
Пользуясь таким уравнением, исследователь избавляется от необходимости
переводить всякий раз условия опыта в кодированные переменные
60. Планирование активного эксперимента
При планировании экспериментов чаще всего применяются планы1-ого и 2-ого порядков. Планы более высоких порядков
применяются редко из-за их большой вычислительной сложности
Планы 1-ого порядка – это планы, которые позволяют провести
эксперимент для отыскания уравнения регрессии, содержащее
только первые степени факторов и их произведения
k
y b0 bi xi
i 1
k
b
i ,u 1
i i
iu
xi xu
k
b
i , j 1
i j u
iju
xi x j xu ...
Планы 2-ого порядка – это планы, которые позволяют провести
эксперимент для отыскания уравнения регрессии, содержащие вторые
степени факторов
k
k
2
y b0 bi xi bii xi
i 1
i 1
k
b
i ,u 1
i u
iu
xi xu ...
61. Планирование первого порядка
• В качестве факторов выбираются толькоконтролируемые и управляемые факторы
(переменные)
• Обеспечивается возможность независимого
изменения каждого из факторов и
поддержание его на определенном уровне
• Для каждого фактора указывается интервал
(+/-), в пределах которого ставится
исследование
62. Представления плана эксперимента (на примере эксперимента с 3-мя независимыми факторами)
b0, b1, b2, b3 – коэффициентырегрессии
xi*xu – члены двойного
взаимодействия
Уравнением регрессии
3
y b0 bi xi
i 1
3
b
i ,u 1
i u
ui
xi xu b123 x1 x 2 x3
Табличное (матричное) представление
x1*x2*x3 – члены тройного
взаимодействия
План
Геометрическое представление
Номер
опыта
Результат
y
x0
x1
x2
x3
x1x2
x1x3
x2x3
x1x2x3
1
+1
-1
-1
-1
+1
+1
+1
-1
y1
2
+1
+1
-1
-1
-1
-1
+1
+1
y2
3
+1
-1
+1
-1
-1
+1
-1
+1
y3
4
+1
+1
+1
-1
+1
-1
-1
-1
y4
5
+1
-1
-1
+1
+1
+1
-1
+1
y5
6
+1
+1
-1
+1
-1
-1
-1
-1
y6
7
+1
-1
+1
+1
-1
+1
+1
-1
y7
8
+1
+1
+1
+1
+1
-1
+1
+1
y8
63. Свойства матрицы представления эксперимента
1. Свойство симметричности – алгебраическая сумма элементов векторстолбца каждого фактора равна нулю (за исключением столбца,соответствующего свободному члену)
n
X
j 1
0,
ij
i = номер фактора, j – номер опыта
2. Свойство нормирования – сумма квадратов каждого столбца равна
числу опытов
n
X
j 1
2
ij
n;
3. Свойство ортогональности – скалярное произведение всех векторстолбцов (сумма почленных произведений элементов любых вектор
столбцов) равно нулю
n
X
j 1
ij
X uj 0, i u
64. Определение коэффициентов b уравнения регрессии
Методом наименьших квадратов находятсяоценки b коэффициентов
По свойствам матрицы планирования
- (ссимметри ность) b0 X 1 j 0;
y b0 b1 x1 b2 x2
(нормирования) b1 X 1 j nb1 ;
2
2
y j y j min
n
(ортогональность) b2 X 1 j X 2 j 0;
bi
j 1
n
2 y j b0 b1 X 1 j b2 X 2 j X 1 j 0;
b1
j 1
n
y
j 1
1j
n
n
j 1
j 1
n
X 1 j b0 X 1 j b1 X 1 j b2 X 1 j X 2 j 0;
2
j 1
Получаем
n
b1
y X
j 1
j
n
1j
; b2
n
y X
j 1
j
n
n
b12
y j X 1 X 2 j
j 1
n
n
2j
; b0
y X
j 1
; b123
y X
j 1
0j
n
n
j
j
1
n
X 2 X3 j
65. Планирование второго порядка
Применяется если
описание функции отклика
первым порядком
получается недостаточным
(например, процесс носит
нелинейный характер)
Каждый фактор
варьируется не менее чем
на трех уровнях – полный
эксперимент содержит 3^k
(k – количество факторов)
опытов.
Опыты проводятся
План 2-ого порядка при k=2 n=1
2
2
y b0 b1 x1 b2 x2 b11 x1 b22 x2 b12 x1 x2
1. В «крайних точках» - как в
планировании 1-ого порядка
2. В «звездных точках» - xi=(+/-)a,
xj=0, 1,…,n; 1,…,n; i!=j
3. В «центре» - xi=0, j=1,2,3,…,n
Уравнение регрессии для
эксперимента с 2-мя факторами































































 Математика
Математика








