Похожие презентации:
Леонардо из Пизы
1. Леонардо из Пизы
Месяцы0 1 2 3 4 5 6 7 8 9 10 11 12 и т.д.
Пары кроликов
0 1 1 2 3 5 8 13 21 34 55 89 144 и т.д.
Ряд чисел
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д.
2. РЯД ФИБОНАЧЧИ
Одна из задач гласила «Сколькопар кроликов в один год от одной
пары родится». Размышляя на
эту тему, Фибоначчи выстроил
ряд
цифр.
Особенность
последовательности чисел в том,
что каждый ее член, начиная с
третьего, равен сумме двух
предыдущих 2 + 3 = 5; 3 + 5 = 8;
5 + 8 = 13, 8 + 13 = 21; и т.д., а
отношение смежных чисел ряда
приближается к отношению
золотого деления. Так, 21 : 34 =
0,617, а 34 : 55 = 0,618. Это
отношение
обозначается
символом Ф.
3. Ряд Фибоначчи
Ряд Фибоначчи (1, 1, 2, 3, 5, 8) и открытый им же «двоичный» ряд гирь 1, 2,4, 8, 16...
Также можно отыскать общую математическую формулу, из которой
получаются и «двоичный» ряд, и ряд Фибоначчи. А может быть, эта
формула даст нам новые числовые множества, обладающие какими-то
новыми
уникальными
свойствами?
Действительно, зададимся числовым параметром S, который может
принимать любые значения: 0, 1, 2, 3, 4, 5... Рассмотрим числовой ряд S + 1
первых членов которого – единицы, а каждый из последующих равен сумме
двух членов предыдущего и отстоящего от предыдущего на S шагов. Если
n-й член этого ряда мы обозначим через φS (n), то получим общую формулу
φS
(n)=φS
(n–1)+φS
(n–S–1).
Очевидно, что при S = 0 из этой формулы мы получим «двоичный»
ряд, при S = 1 – ряд Фибоначчи, при S = 2, 3, 4. новые ряды чисел, которые
получили
название
S-чисел
Фибоначчи.
В общем виде золотая S-пропорция есть положительный корень уравнения
золотого
S-сечения
xS+1
–
xS
–
1
=
0.
Нетрудно показать, что при S = 0 получается деление отрезка
пополам, а при S = 1 – знакомое классическое золотое сечение.
4. Прямоугольник
Прямоугольникс
таким
отношением
сторон
стали
называть
золотым
прямоугольником. Он обладает
интересными свойствами. Если от
него
отрезать
квадрат,
то
останется
вновь
золотой
прямоугольник. Этот процесс
можно
продолжать
до
бесконечности. А если провести
диагональ первого и второго
прямоугольника, то точка их
пересечения будет принадлежать
всем
получаемым
золотым
прямоугольникам.
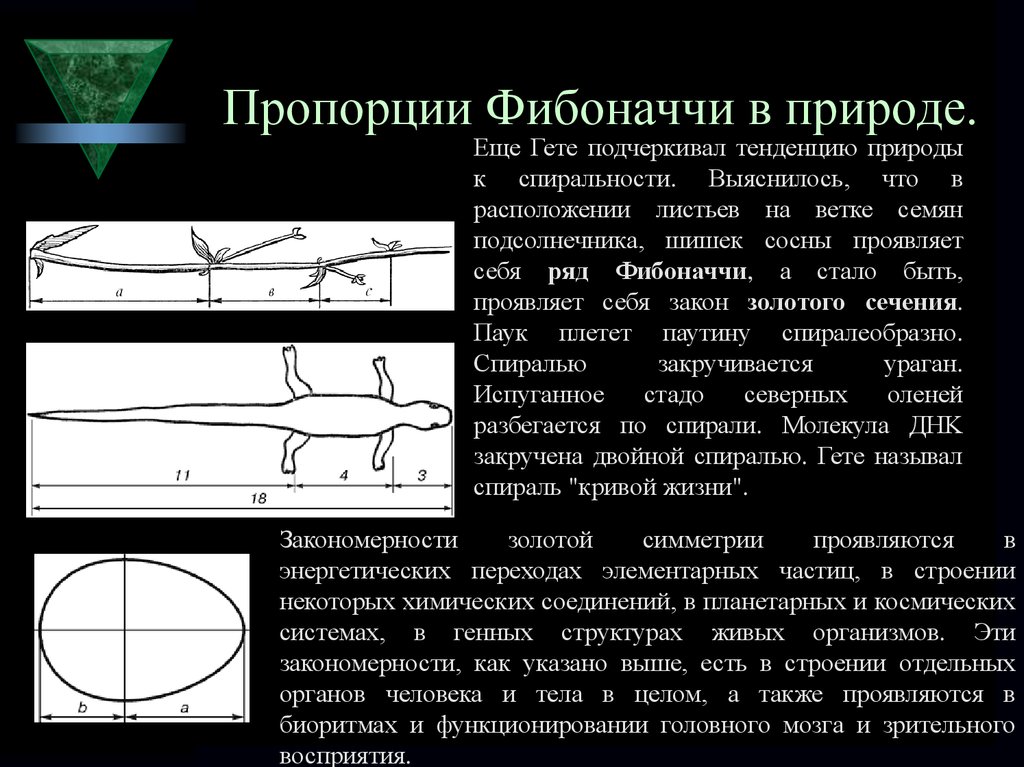
5. Пропорции Фибоначчи в природе.
Еще Гете подчеркивал тенденцию природык спиральности. Выяснилось, что в
расположении листьев на ветке семян
подсолнечника, шишек сосны проявляет
себя ряд Фибоначчи, а стало быть,
проявляет себя закон золотого сечения.
Паук плетет паутину спиралеобразно.
Спиралью
закручивается
ураган.
Испуганное
стадо
северных
оленей
разбегается по спирали. Молекула ДНK
закручена двойной спиралью. Гете называл
спираль "кривой жизни".
Закономерности
золотой
симметрии
проявляются
в
энергетических переходах элементарных частиц, в строении
некоторых химических соединений, в планетарных и космических
системах, в генных структурах живых организмов. Эти
закономерности, как указано выше, есть в строении отдельных
органов человека и тела в целом, а также проявляются в
биоритмах и функционировании головного мозга и зрительного
восприятия.
6. Пирамиды
Многиепытались разгадать
секреты пирамиды в Гизе. В
отличие от других египетских
пирамид это не гробница, а
скорее
неразрешимая
головоломка
из
числовых
комбинаций. Ключ к геометроматематическому
секрету
пирамиды в Гизе, так долго
бывшему
для
человечества
загадкой, в действительности
был
передан
Геродоту
храмовыми
жрецами,
сообщившими
ему,
что
пирамида построена так, чтобы
площадь каждой из ее граней
была равна квадрату ее высоты.
Площадь треугольника = 78.320
Площадь квадрата = 78.400
7.
Длина грани пирамиды в Гизеравна 783.3 фута (238.7 м),
высота пирамиды -484.4 фута
(147.6 м). Длина грани, деленная
на
высоту,
приводит
к
соотношению Ф=1.618. Высота
484.4 фута соответствует 5813
дюймам (5-8-13) - это числа из
последовательности Фибоначчи.
Эти
интересные наблюдения
подсказывают, что конструкция
пирамиды
основана
на
пропорции Ф=1,618.
Также
таким
пропорциям
подчиняются и
мексиканские
пирамиды. Только в поперечном
сечении пирамиды видна форма,
подобная лестнице. В первом
ярусе 16 ступеней, во втором 42
ступени и в третьем - 68
ступеней.






 Биографии
Биографии