Уравнения и неравенства с параметрами. Часть 1

1. Уравнения и неравенства с параметрами

Часть 1

2. План

1.
2.
3.
Что такое задача с параметром?
Аналитический метод решения
задач с параметрами.
Графический метод решения задач с
параметрами.

3. Что такое задача с параметром

F x, a 0
Задачи:
1. Решить уравнение (найти все пары
чисел (х, а), которые удовлетворяют
данному уравнению).
Например: решить уравнение в целых числах
ax 4 ax 2 1 0
2.
Для каждого значения а решить
уравнение относительно
переменной х.

4. Задача с параметром первого типа

Пример:
Решить уравнение относительно х:
b
2
b x 1 b
где b - параметр и может принимать
значения из множества M 0,1,3 .
Семейство уравнений: 0 x 1
0 x 0
6 x 2

5. Задача с параметром первого типа

Определение
Решить уравнение с переменной х и
параметром а – это значит на множестве R
решить семейство уравнений, получающихся
из данного уравнения при подстановке вместо
параметра любых значений из его области
изменения.
Замечание. Аналогично определяются понятия
неравенства, системы уравнений, системы неравенств
с параметром. Кроме того, часто встречаются задачи,
в условии которых содержится не один, а несколько
параметров.

6. Задача с параметром второго типа

Примеры
1. Для каких значений a и b уравнение
имеет только 2 различных корня?
x ax b x a 0
4
3
2
2
2. При каких значениях а минимум
функции больше 1?
f ( x) ax x 5 x 6
2

7. Методы решения задач с параметрами

Аналитические
Графические

8. Аналитические приемы

1. «В лоб»
Этапы:
- обнаружение критических значений
параметра и разбиение множества
параметров на подмножества
- решение задачи на каждом из выделенных
подмножеств
- запись ответа

9. Решение «в лоб»

Пример
2
a
1
x
2 2a 1 x 4a 3 0
Решить уравнение:
Решение:
1 этап.
1 вывод. Уравнение степени не выше 2
2 вывод. Рассмотреть значения параметра,
влияющие на степень уравнения.
1 промежуточный результат:
Первое «критическое» значение параметра а=1

10. Решение «в лоб»

Квадратное уравнение
D
2
2a 1 a 1 4a 3 5a 4
4
2 промежуточный результат:
4
Второе «критическое» значение параметра: a
5
Результат первого этапа: разбиение множества
параметров на 4 подмножества:
; 0,8 0,8 0,8;1 1;
1

11. Схема решения

2 этап:
1.
2.
3.
a ; 0,8 уравнение не имеет корней,
поскольку дискриминант квадратного уравнения
отрицательный.
а=-0,8 – дискриминант квадратного уравнения
1
обращается в ноль, и уравнение имеет корень х=
a 0,8;1 1; уравнение является квадратным с 3
положительным дискриминантом, и его корнями
являются два различных числа: 2a 1 5a 4
x
a 1
2 a 1 5a 4
x
a 1
4.
а=1 – уравнение имеет вид: 6х+7=0 и единственный
корень:
7
x
6

12. Схема решения

3 этап.
Ответ:
при a ; 0,8 корней нет;
1
при а=-0,8 х= ;
3
при a 0,8;1 1;
при а=1
7
x
6
2 a 1 5a 4
x
a 1
21 1 5a 4
x
a 1

13. Решение «в лоб»

Замечание.
При определении пограничных
значений параметра следует обращать
внимание на:
- обращение в 0 старшего коэффициента;
- обращение в 0 дискриминанта;
- границы области определения
параметра;
- ОДЗ уравнения (неравенства…) и др.

14. Аналитические приемы

2. Метод равносильных переходов
Используются теоремы о равносильных и
неравносильных преобразованиях
уравнений (неравенств, систем).
Пример: решить неравенство
x a x 1

15. 2. Метод равносильных переходов

Решение:
x 1 0
x a 0
x 1 0
x a x 2 2 x 1
x 1
( I )
x a
x 1
x a
x 1
x 2 x 1 a 0
x 1
( II ) 2
x x 1 a 0

16. Решение

x 1
( I )
x a
при
при
a 1 решений нет
a>1
x a; 1
-а
-1
х

17. Решение

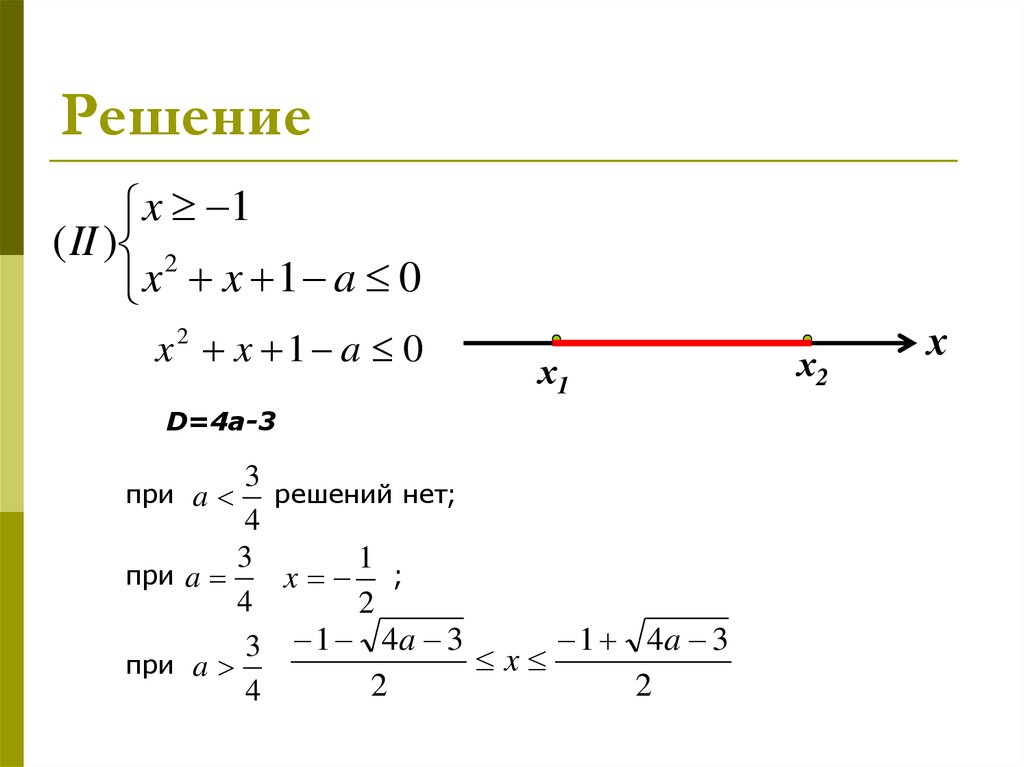
x 1
( II ) 2
x x 1 a 0
x2 x 1 a 0
х1
D=4a-3
3
решений нет;
4
3
1
при a
x ;
4
2
3 1 4a 3 x 1 4a 3
при a
2
2
4
при
a
х2
х

18. Решение

Ответ:
3
при a
решений нет;
4
при a
3
4
x
3
a 1
при
4
при a>1
1
2
1 4a 3
1 4a 3
x
2
2
1 4a 3
a x
2

19. Аналитические приемы

3. Замена переменной
1.
2.
исходя из свойств какой-то функции
упрощающая вычисления

20. 3. Замена переменной

Пример 1.
1 x a x
2
При каких значения параметра а неравенство
имеет решения
ОДЗ: 1 x 1
x=sin(t),
t ;
2 2
1 sin 2 t a sin t cos t a sin t cos t sin t a
2 sin t a
4
так как
2 2 sin t 2
4
, то a
2

21. 3. Замена переменной

Пример 2.
При каких значениях параметра с система имеет
3x
8 y 3 x 3
4 y 1
2
2
2
решение?
2
2
x
y
c
23 x 28 y 3 x 3 24 y 1 2 3 x 4 y 2 4 y 3 x 8 2
(1)
3 x 4 y
Пусть z 2
8
z 2 0 , z=4
z
2 3 x 4 y 2 2 3x 4 y 2
2 2
2
2
x y 2 c
3x
8 y 3 x 3
4 y 1
3x 4 y 2
x 2 y 2 c
2 4y
x
3
25 y 2 16 y 4 9c 0
2 4y
x
3
2 4 y 2 9 y 2 9c
36
c
225

22. Аналитические приемы

4. Использование свойств функций
1. монотонность
2. ограниченность
3. свойства линейной и квадратичной
функций

23. 4. Использование свойств функций

Пример 1. (ограниченность)
При каких целых значениях параметра k
система имеет решения? arctgx 2 (arccos y ) 2 2 k
0 arctgx
2
arctgx arccos y
2
2
0 arccos x 2
2
4
0 arctgx arccos x
2
2
5
4
2
2
5
0 2k
4
k 0
k 1

24. 4. Использование свойств функций

Пример 2. (монотонность)
При каких значениях параметра а уравнение имеет
ровно 3 корня?
(1)
| x a|
2
x 2 2 x
4
log
f t1 f t 2
2
2| x a|
2
3
x
2x 3 2
3
2 log 3 x 2 x 3 2
x 2 2 x 1
2
log 1 2 | x a | 2 0
x 2 2 x
log 2 | x a | 2
3
log 3 x 2 2 x 3 22| x a| log 3 2 | x a | 2
f (t ) 2t log 3 (t 2)
(1) x 1 2 x a
2

25. 4. Использование свойств функций

Пример 3.
Найдите все значения параметра а, при
которых корни уравнения лежат по разные
стороны от 1 a 2 1 x 2 2a 1 x 3 0
1 вывод: a 2 1 0 И 2a 1 2 12 a 2 1 0
2 вывод: a 2 1 a 2 1 2a 1 3 0
2
2
a
1
a
2a 3 0
2
16
a
4a 13 0

26. Аналитические приемы

5. Поиск необходимых условий
1. использование симметрии
аналитических выражений
2.
присутствует требование единственности
решения
есть аналитическое выражение,
обладающее симметрией относительно
одной из переменных
поиск «выгодной» точки

27. 5. Поиск необходимых условий

Пример 1.
При каких значениях параметра а
система имеет единственное решение?
4
a x 1 y 1 | x |
2
2
x
y
1
Необходимое условие: х=0.
y a 1
2
y 1
a 0
a 2

28. 5. Поиск необходимых условий

Пример 2.
При каких значениях параметра а уравнения
равносильны?
(1) sin( 2 x) a sin x 2a cos x
2
(2) 2 cos(2 x) a 5a cos x 2
sin x a
(1) (sin x a)( 2 cos x 1) 0
cos x 0,5
a 2 2,5a 1 0
a 2
a 0,5

29. 6. Рассмотрение параметра как равноправной переменной

Пример:
Найти все значения параметра, при которых
уравнения имеют общий действительный
корень.
2
x
(1) x 4a 0
2 2
(2) a x ax 4a 0
2 2
a x ax 4a 0
2
x x 4a 0

30. 7. Решение относительно параметра

Пример:
a a sin x sin x
При каких значениях параметра а уравнение
имеет решение?
0 t 1
2
a
t
t
a
t 2 a
2
2
4
a a 2t 1 t t 0
a a t t
sinx=t
a t t 1
2
a t2 t
0 t 1
2
a
t
t
t 2 a
0 t 1
2
a
t
t
f (t ) t 2 t
1
4 ;0
2
0;1

31. Задание

;
1.
2.
3.
Решите неравенство: 2a(a-2)x>a-2
Решите уравнение: a 2 x x 2 a 2 a x
Найдите те значения параметра а, при
которых разные корни уравнения
расположены по одну сторону от 2.
x 4ax 1 2a 4a 0
2
4.
2
При каких значениях параметра уравнения
имеют общие корни?
x
x a 0
2
2
4a x ax a 0
2
2

32. Задание

5. Решить уравнение: x(2 x 1) 1 x a
6. Решить систему (a 2 a) sin x 2 cos y a 5
2
уравнений:
2
3 sin x cos y 4
2
7. Найти все значения параметра, при
каждом из которых уравнение имеет три
корня: 9a log 2 (| x 2 4x 3 | 1) 33a |x 4 x 3| log 2 (1 3a 2a 2 )
8.При каких значениях а система имеет
единственное решение? (| x | 1)a y cos x
2
2
sin
x
y
1
2
2