Похожие презентации:
Способы решений уравнений и неравенств с параметром
1. СПОСОБЫ РЕШЕНИЙ УРАВНЕНИЙ И НЕРАВЕНСТВ С ПАРАМЕТРОМ.
2.
Способы решения
параметрических уравнений и
неравенств׃
алгебраический,
аналитический,
функционально – графический;
использование методов
математического анализа.
3. Алгебраический способ решения иррациональных уравнений с параметрами.
При каких х уравнение x 3 2 x аимеет единственное решение?
x 3 4x 4x à õ
2 õ à 0
2
2
49
6;
8
4.
2 способу
х
3
y 2x a
49
6;
8
5. . При каких значениях параметра уравнение имеет на промежутке не меньше 3 корней?
. При каких значениях параметра1
a
cos x a cos x 0
3
3
уравнение
2
имеет на промежутке
5
4 ; 3
3 корней?
1 a
t a t 0
3 3
2
2
1
D a 0
3
не меньше
6.
1t
[
1
;
]
1
2
t [ 1; 1 )
2
2
t ( 1; 1 ]
1
2
t ( 1 ; 2 ]
2 2 2
1 1 2
a 1; ;
3 3 2
7. При каких а неравенство верно для всех х?
При каких а неравенство2
2
2à 4 a 3 sin x cos 2 x 0
верно для всех х?
at 4a 1 t 6a 4 0
2
8. 2 способ
4 cos xa
3 sin x
2
2
2
2
f ( x)
4 cos x 3
2
2 3 sin x
2
2
11
3
a min f ( x)
11
3
a
11
9.
• При каких неравенство ax x 4 x 3 1• выполняется для всех x ?
2
y x 2 4 x 3
y 1 ax
1 a 4 2 2
10. 2 способ
x 2 4 x 3 1 axx 2 4 x 3 0
1 x 3
2
2
x 4 x 3 1 ax
x (a 4) x 4 0
1;4 2 2









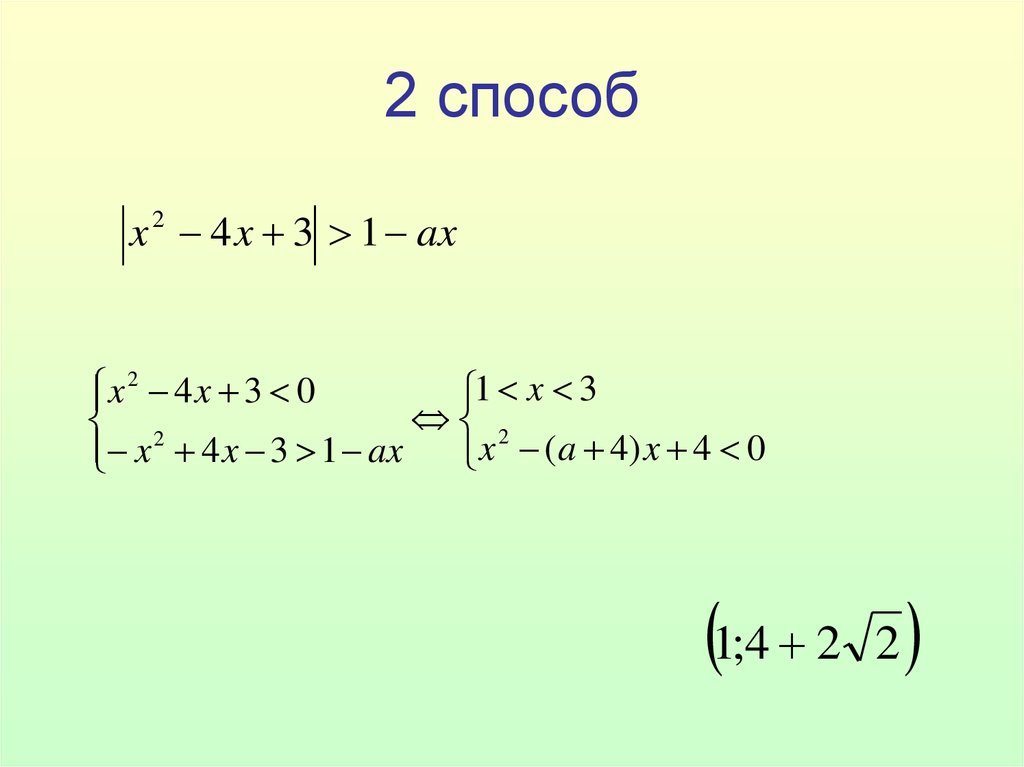
 Математика
Математика








