Теория и методы дискретных вычислений

1.

ТЕОРИЯ И МЕТОДЫ ДИСКРЕТНЫХ
ВЫЧИСЛЕНИЙ
Лектор –
доктор технических наук, профессор
Князьков Владимир Сергеевич
Кафедра ЭВМ
Вятский государственный университет
1

2. А. Основная литература

Волченская Т.В., Князьков В.С. Компьютерная математика: ч.2.
Теория графов: Учеб. пособие. - 2007. – 124 с.-//www.intuit.ru
Харари Ф. Теория графов: учебник для вузов / Ф. Харари. – М.:
УРСС, 2006.
Иванов Б.Н. Дискретная математика. Алгоритмы и программы.
Расширенный курс. – М: Известия, 2011. – 512 с.
http://www.intuit.ru/studies/courses/1033/241/info
1.
Электронные лекции
2.
Примеры
3.
Тесты – в итоге СЕРТИФИКАТ ИНТУИТ
2

3. Б. Дополнительная литература

1.
Белоусов А. И., Ткачев С. Б. Дискретная математика. – М.: Изд-во МГТУ
им Н.Э. Баумана, 2001. – 744 с.
2.
Оре О. Графы и их применение: Пер. с англ. - Изд.3-е стереотипное. –
М.: КомКнига, 2006.
3.
Харари Фрэнк Теория графов = Graph theory/Пер. с англ. и предисл. В.
П. Козырева. Под ред. Г.П.Гаврилова. Изд. 2-е. — М.: Едиториал УРСС,
2003. — 296 с.
4.
Асанов М. О., Баранский В. А., Расин В. В. Дискретная математика:
графы, матроиды, алгоритмы — НИЦ РХД, 2001. — 288 с.
5.
5. Кормен,Томас Х., Лейзерсон, и др. Алгоритмы: построение и анализ, 2е издание. Пер. с англ. — М.:Изд. дом "Вильямс", 2010. — 1296 с.:
6.
6. Дискретная математика, Асеев Г.Г.
7.
7. Комбинаторика и теория графов, Носов В.А.
8.
8. Дискретная математика, Асанов М.О., Графы, Матроиды, Алгоритмы
3

4. 1. Введение и области применения теории графов 2. Способы представления графов 3. Основные операции на графах

4

5. Введение

В последние годы особую важность приобрели те разделы
математики, которые имеют отношение к развитию
цифровых устройств, цифровой связи и цифровых
вычислительных машин. Базой для преподавания этих
дисциплин наряду с классическими методами анализа
непрерывных
физических
моделей
стали
алгебраические, логические и комбинаторные методы
исследования
различных
моделей
дискретной
математики.
Значительно возросла популярность теории графов - ветви
дискретной математики. Графы встречаются во многих
областях под разными названиями: “структуры” в
гражданском
строительстве,”сети”
в
электронике,
”социограммы”
в
социологии
и
экономике,
“молекулярные структуры” в химии,”дорожные карты”,
электрические или газовые распределительные сети и
т.д.
5

6.

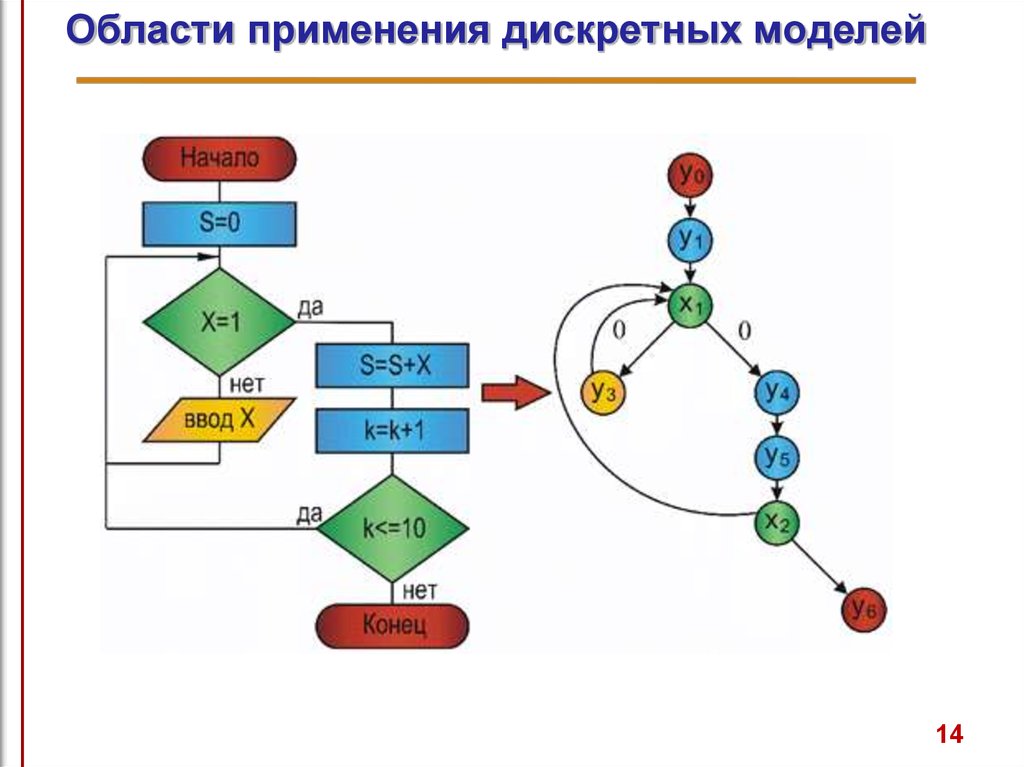
Области применения дискретных моделей
Комбинаторные вычисления находят широкое
применение в различных областях :
Производство РЭА и ВТ
• оптимальное размещение элементов
и трассировка;
разбиение схемы на подсхемы для
реализации блоками и т.д.
6

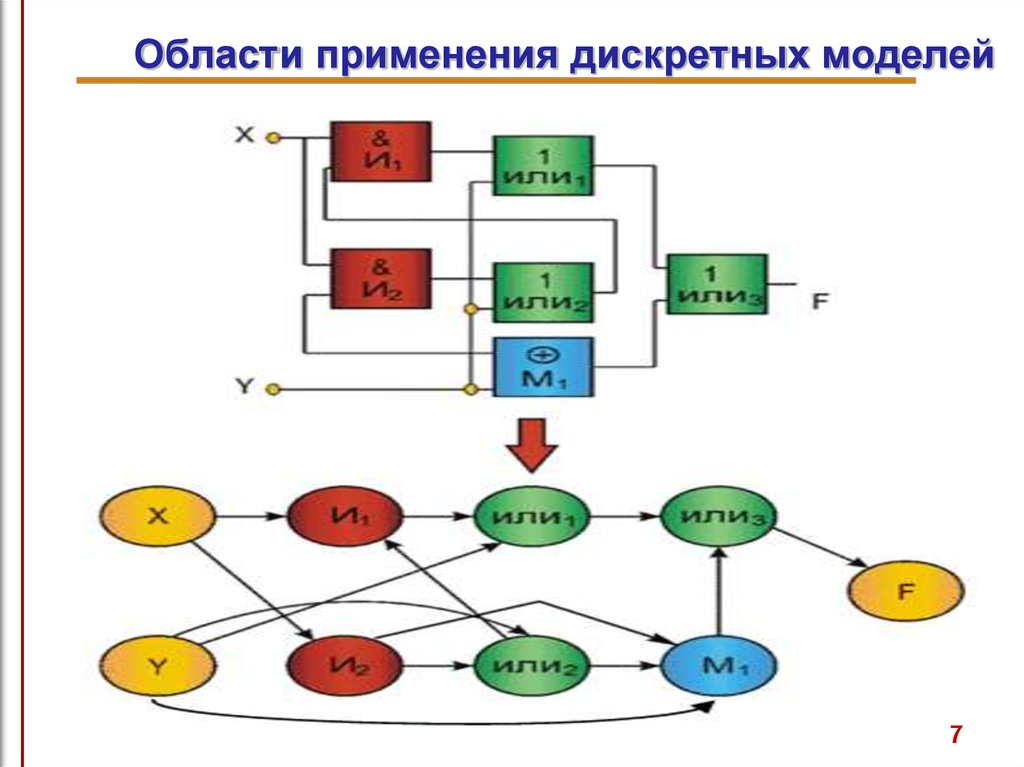
7. Области применения дискретных моделей

7

8.

Области применения дискретных моделей
2. Строительство
-Как построить транспортную сеть в регионе, чтобы
минимизировать затраты на строительство и оптимизировать
транспортные перевозки.
- Как соединить мостами острова в пойме большой реки,
минимизируя затраты и учитывая параметры сейсмостойкости и
прочности.
-Сколько вариантов прокладки трубопроводов между
заданными пунктами?
8

9.

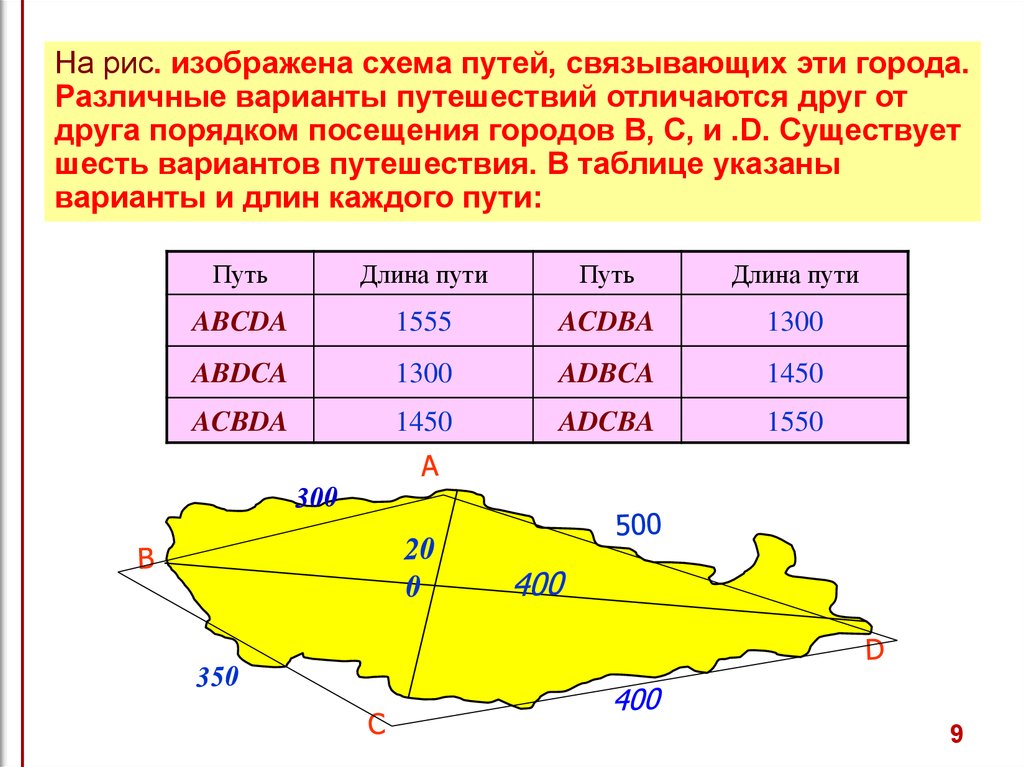
На рис. изображена схема путей, связывающих эти города.
Различные варианты путешествий отличаются друг от
друга порядком посещения городов В, С, и .D. Существует
шесть вариантов путешествия. В таблице указаны
варианты и длин каждого пути:
Путь
Длина пути
Путь
Длина пути
ABCDA
1555
ACDBA
1300
ABDCA
1300
ADBCA
1450
ACBDA
1450
ADCBA
1550
9

10.

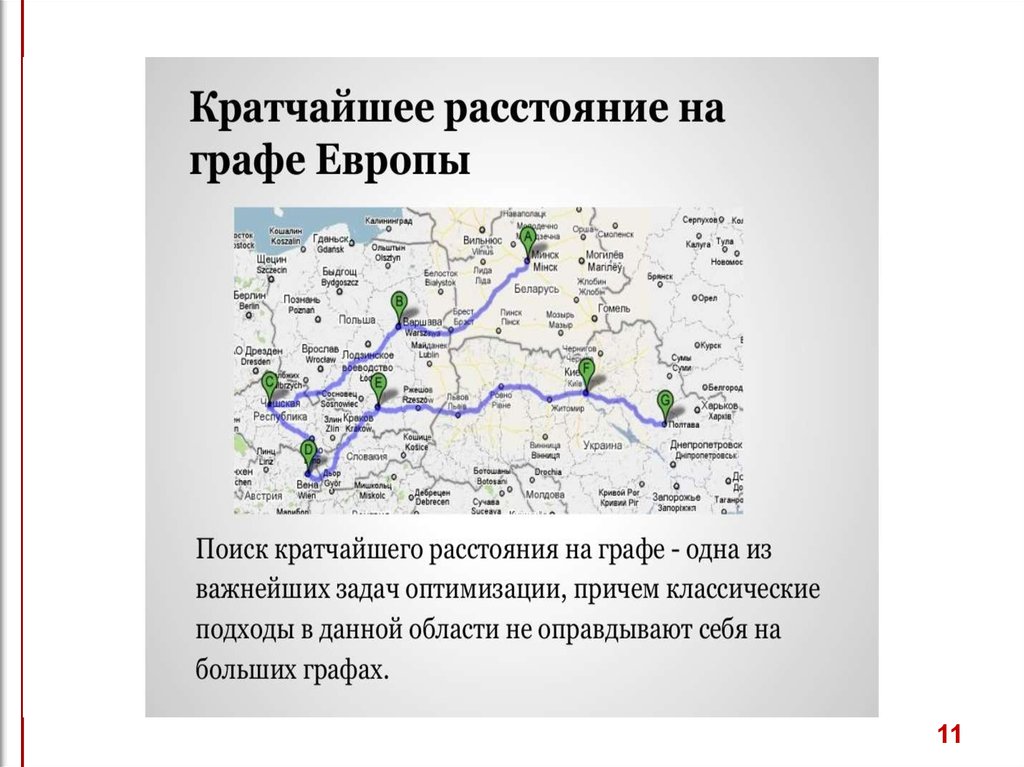
10

11.

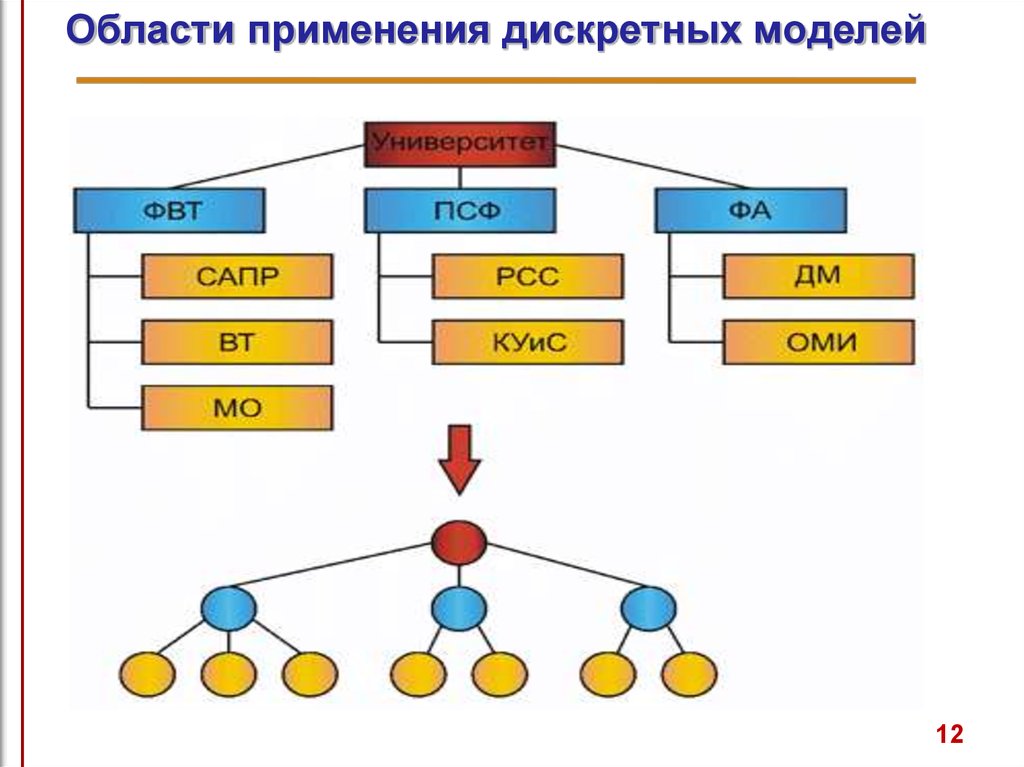
11

12. Области применения дискретных моделей

12

13. Области применения дискретных моделей

-при исследовании так называемой проблемы
оптимизации, возникающей при конструировании
больших систем как технических, так и программных,
например, таких как компиляторы;
-в области проектирования для построения
эффективных алгоритмов и анализа их сложности.;
-при разработке алгоритмов конструкторского
проектирования схем;
-В психологии при анализе совместимости;
-В системах управления…
13

14. Области применения дискретных моделей

14

15.

Графы
и способы их представления
15

16. Основные определения

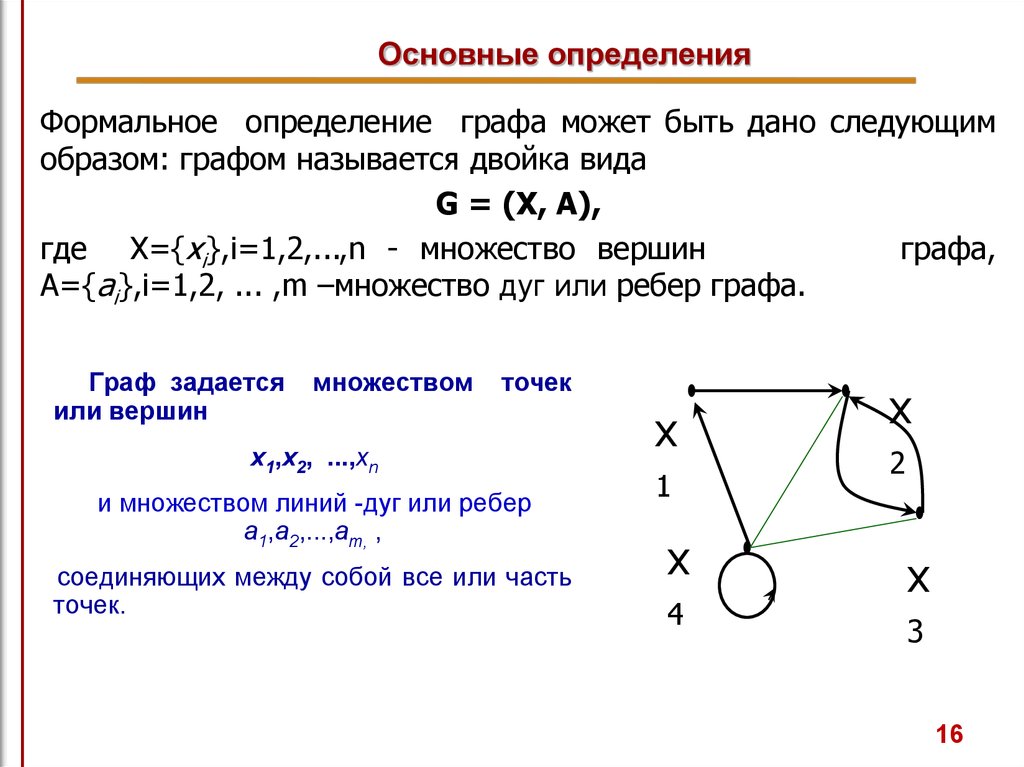
Формальное определение графа может быть дано следующим
образом: графом называется двойка вида
G = (X, A),
где X={xi},i=1,2,...,n - множество вершин
графа,
A={ai},i=1,2, ... ,m –множество дуг или ребер графа.
Граф задается
или вершин
множеством
точек
х1,х2, ...,хn
и множеством линий -дуг или ребер
a1,a2,...,am, ,
соединяющих между собой все или часть
точек.
x
1
x
4
x
2
x
3
16

17. Графы могут быть ориентированными, неориентированными и смешанными

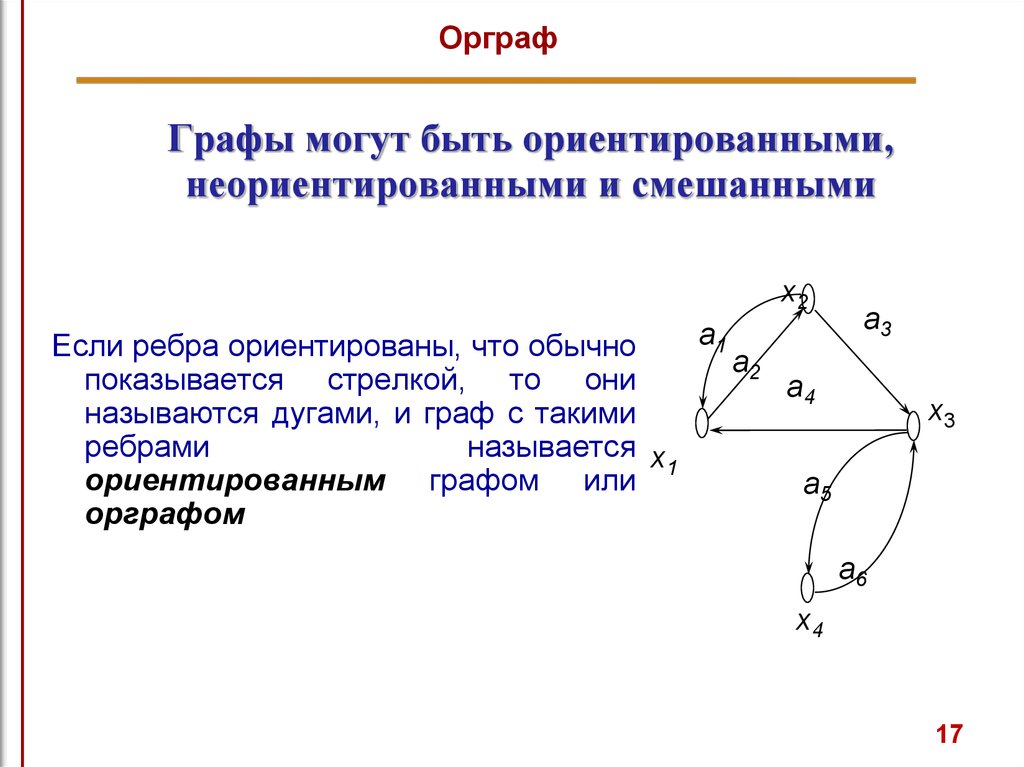
Орграф
Графы могут быть ориентированными,
неориентированными и смешанными
x2
Если ребра ориентированы, что обычно
показывается стрелкой, то они
называются дугами, и граф с такими
ребрами
называется x
ориентированным графом или 1
орграфом
a1
a2
a3
a4
x3
a5
a6
x4
17

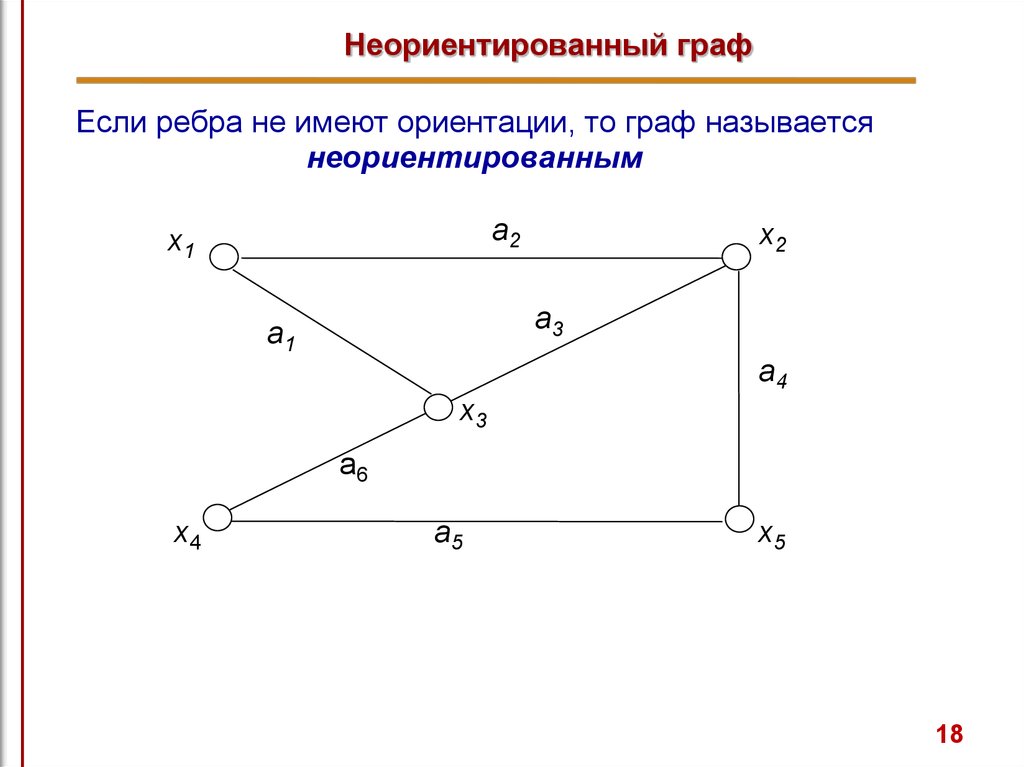
18. Неориентированный граф

Если ребра не имеют ориентации, то граф называется
неориентированным
a2
x1
x2
a3
a1
a4
x3
a6
x4
a5
x5
18

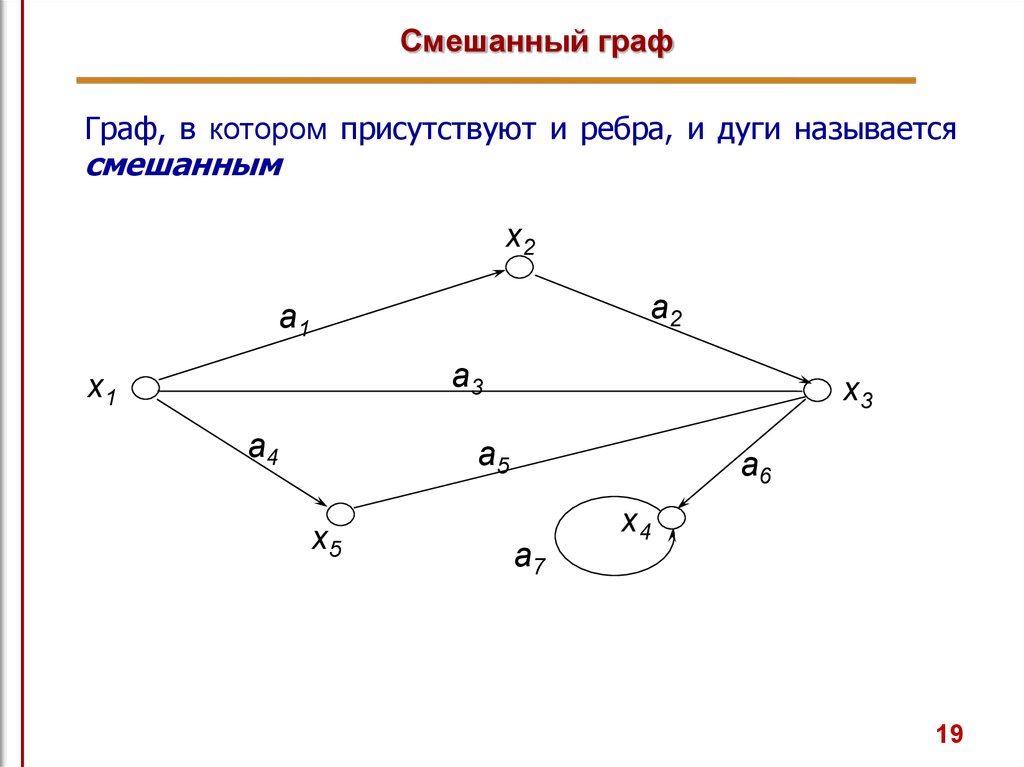
19. Смешанный граф

Граф, в котором присутствуют и ребра, и дуги называется
смешанным
x2
a2
a1
a3
x1
a4
x3
a5
x5
a6
a7
x4
19

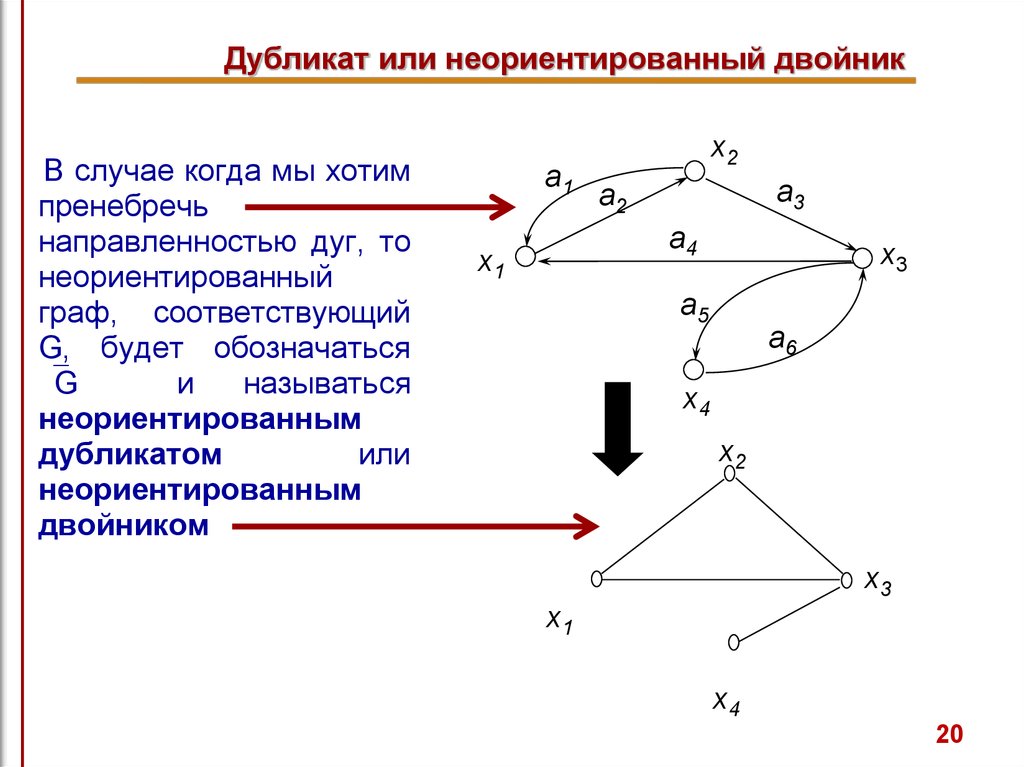
20. Дубликат или неориентированный двойник

В случае когда мы хотим
пренебречь
направленностью дуг, то
неориентированный
граф, соответствующий
G, будет обозначаться
G
и
называться
неориентированным
дубликатом
или
неориентированным
двойником
a1
x2
a3
a2
a4
x1
x3
a5
a6
x4
x2
x3
x1
x4
20

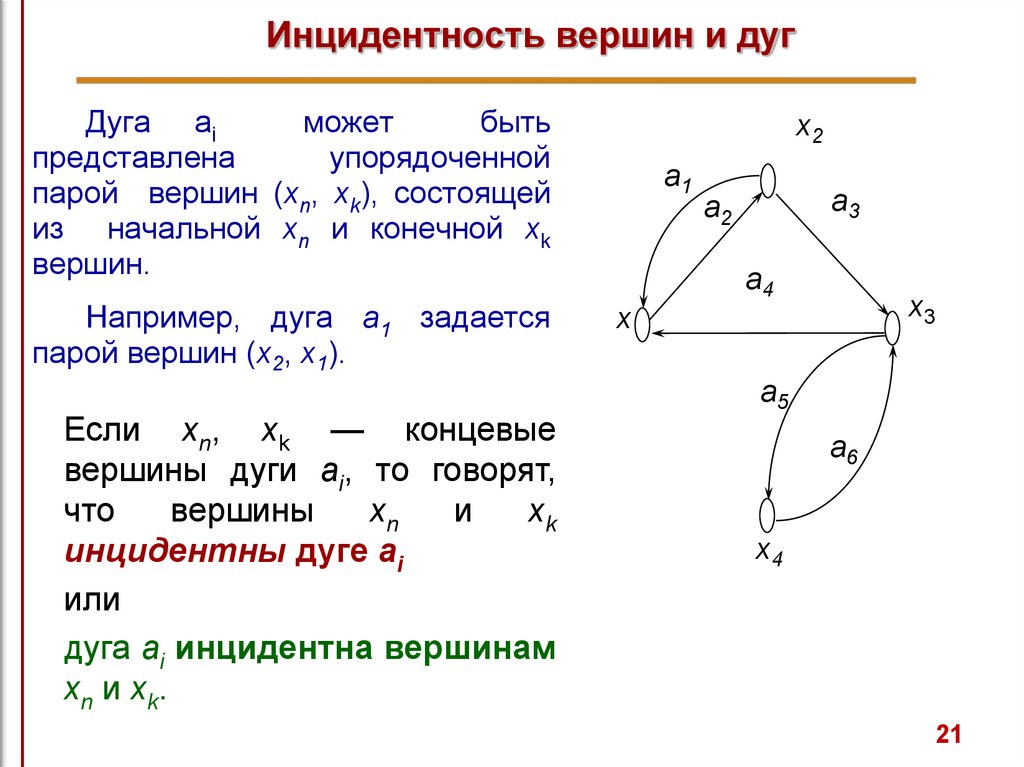
21. Инцидентность вершин и дуг

Дуга ai
может
быть
представлена
упорядоченной
парой вершин (xn, xk), состоящей
из начальной xn и конечной xk
вершин.
Например, дуга a1 задается
парой вершин (x2, x1).
Если xn, xk — концевые
вершины дуги ai, то говорят,
что
вершины
xn
и
xk
инцидентны дуге ai
или
дуга ai инцидентна вершинам
xn и xk.
x2
a1
a3
a2
a4
x3
x1
a5
a6
x4
21

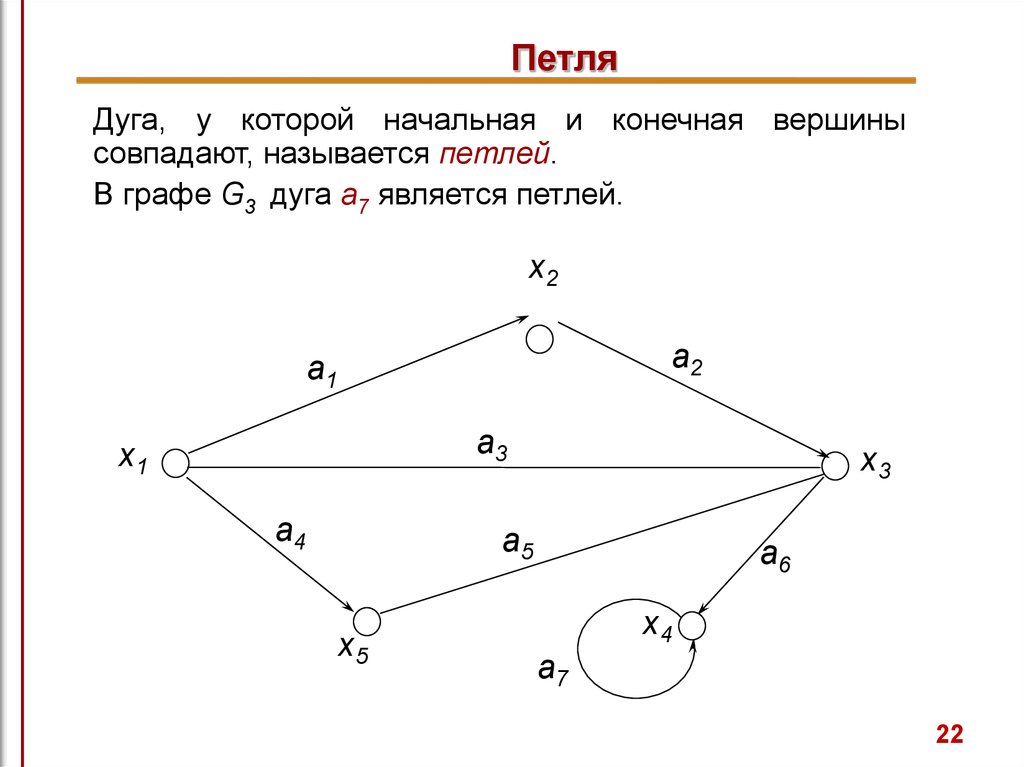
22. Петля

Дуга, у которой начальная и конечная вершины
совпадают, называется петлей.
В графе G3 дуга а7 является петлей.
x2
a2
a1
a3
x1
a4
x3
a5
x5
a6
x4
a7
22

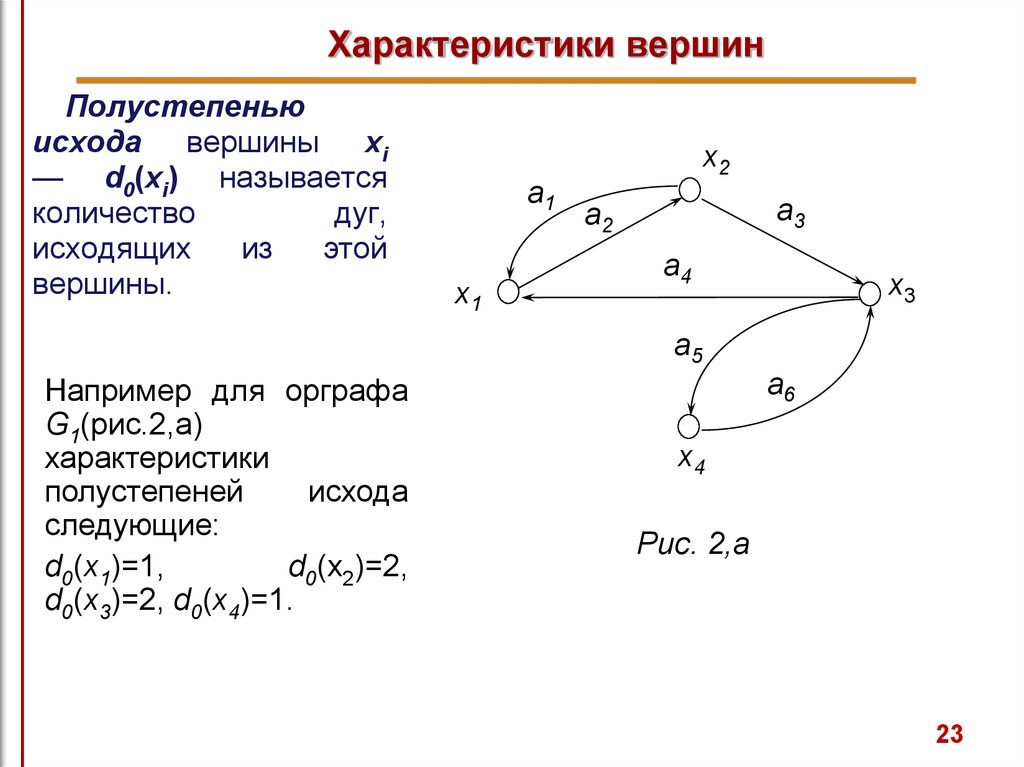
23. Характеристики вершин

Полустепенью
исхода вершины xi
— d0(xi) называется
количество
дуг,
исходящих
из
этой
вершины.
x2
a1
x1
a3
a2
a4
x3
a5
Например для орграфа
G1(рис.2,а)
характеристики
полустепеней
исхода
следующие:
d0(x1)=1,
d0(x2)=2,
d0(x3)=2, d0(x4)=1.
a6
x4
Рис. 2,а
23

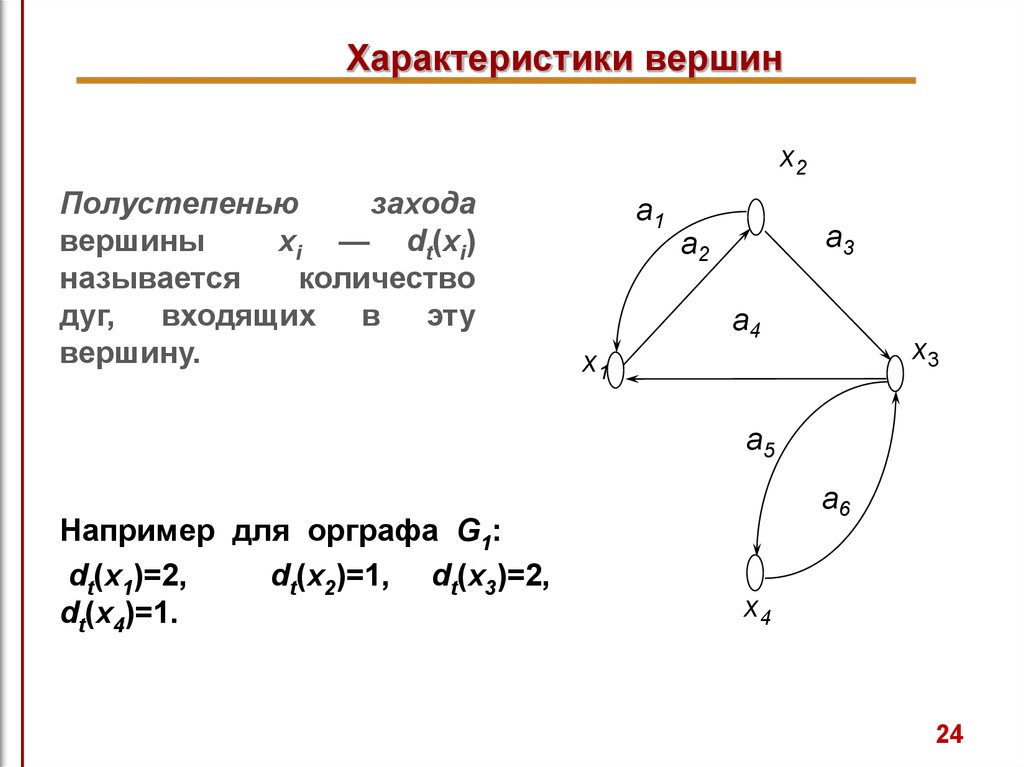
24. Характеристики вершин

x2
Полустепенью
захода
вершины
xi — dt(xi)
называется
количество
дуг, входящих в эту
вершину.
a1
a3
a2
a4
x3
x1
a5
Например для орграфа G1:
dt(x1)=2,
dt(x2)=1, dt(x3)=2,
dt(x4)=1.
a6
x4
24

25. Характеристики вершин

Очевидно, что сумма полустепеней исхода всех вершин
графа,
а также сумма полустепеней захода всех вершин графа
равна общему числу дуг графа, т.е.
d x d x
n
i 1
n
0
i
i 1
t
i
m
где n-число вершин графа, m-число дуг.
25

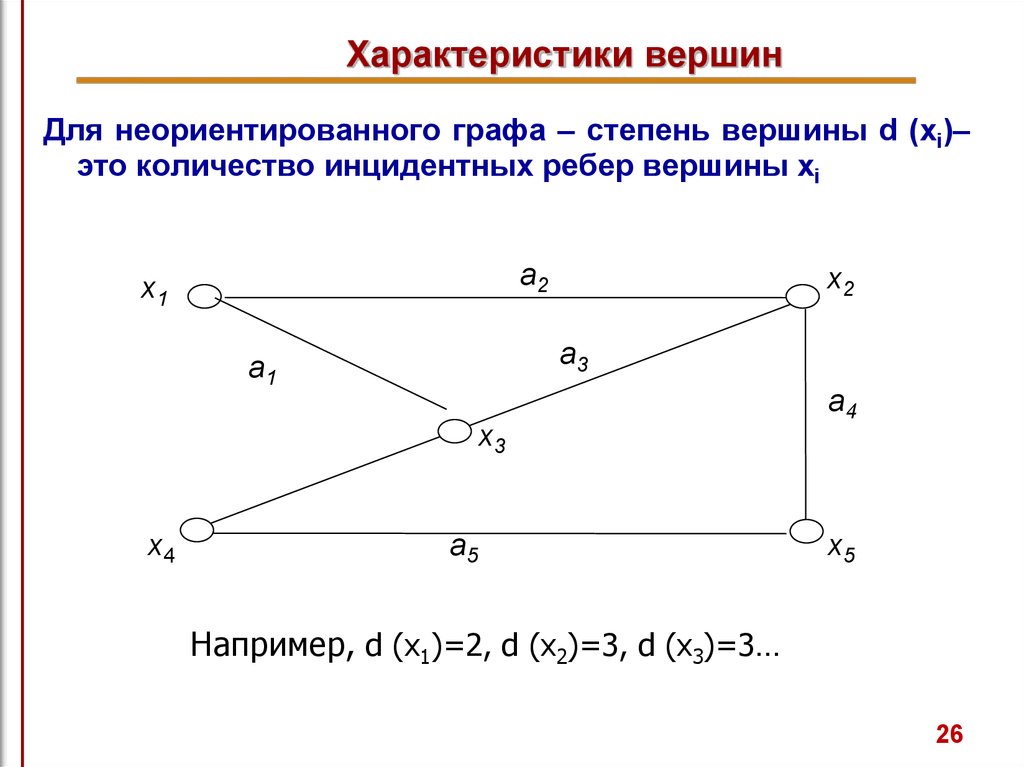
26. Характеристики вершин

Для неориентированного графа – степень вершины d (xi)–
это количество инцидентных ребер вершины xi
a2
x1
x2
a3
a1
a4
x3
x4
a5
x5
Например, d (x1)=2, d (x2)=3, d (x3)=3…
26

27. Способы описания графов

Теоретико-множественное описание
Описание отображениями
Графическое
Матричное
27

28. Теоретико-множественное представление графов

Граф описывается явным перечислением элементов множеств
вершин и дуг.
x2 рис.3 и рис. 4.
Примеры описания приведены для орграфов на
a4
a1
a2
x1
a3
x3
a5
a6
x4
Рис. 3
28

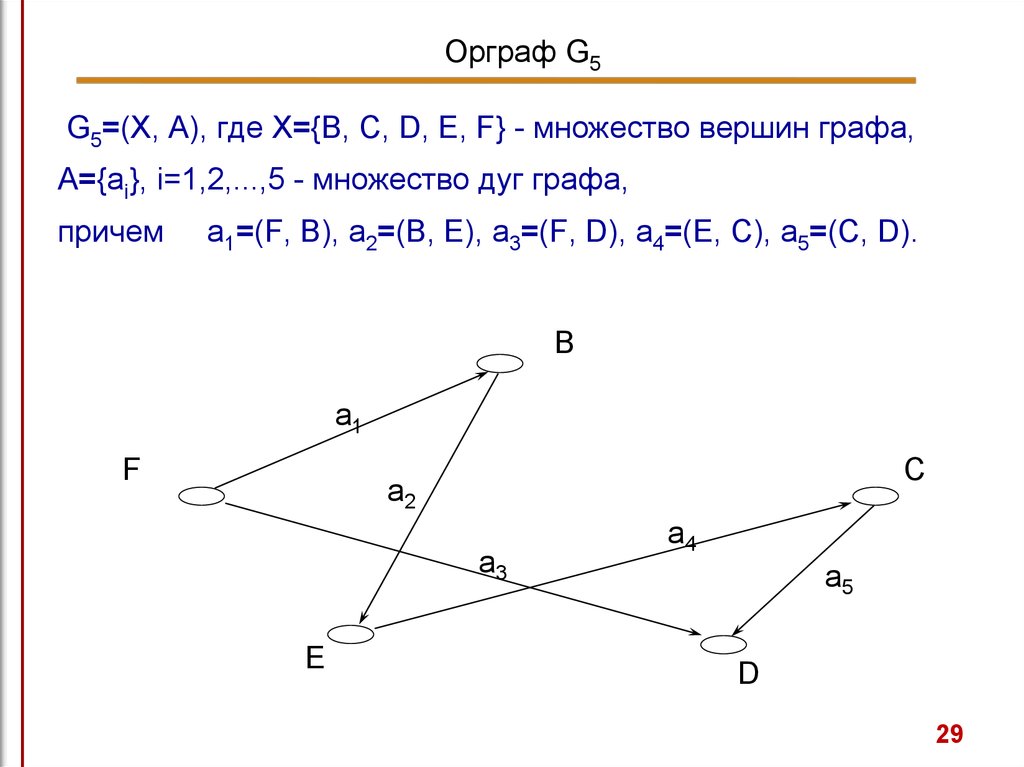
29.

Орграф G5
G5=(X, A), где X={B, C, D, E, F} - множество вершин графа,
A={ai}, i=1,2,...,5 - множество дуг графа,
причем
a1=(F, B), a2=(B, E), a3=(F, D), a4=(E, C), a5=(C, D).
B
a1
F
C
a2
a3
E
a4
a5
D
29

30.

Задание графов отображениями
Описание графов состоит в задании множества вершин Х и
соответствий Г или отображений для каждой вершины.
Соответствием Г называется отображение множества Х
в Х,
Отображением вершины xi — Г(xi) является множество
вершин, в которые существуют дуги из вершины xi, то есть
Г(xi)={ xj: дуга (xi,) xj A}
.
30

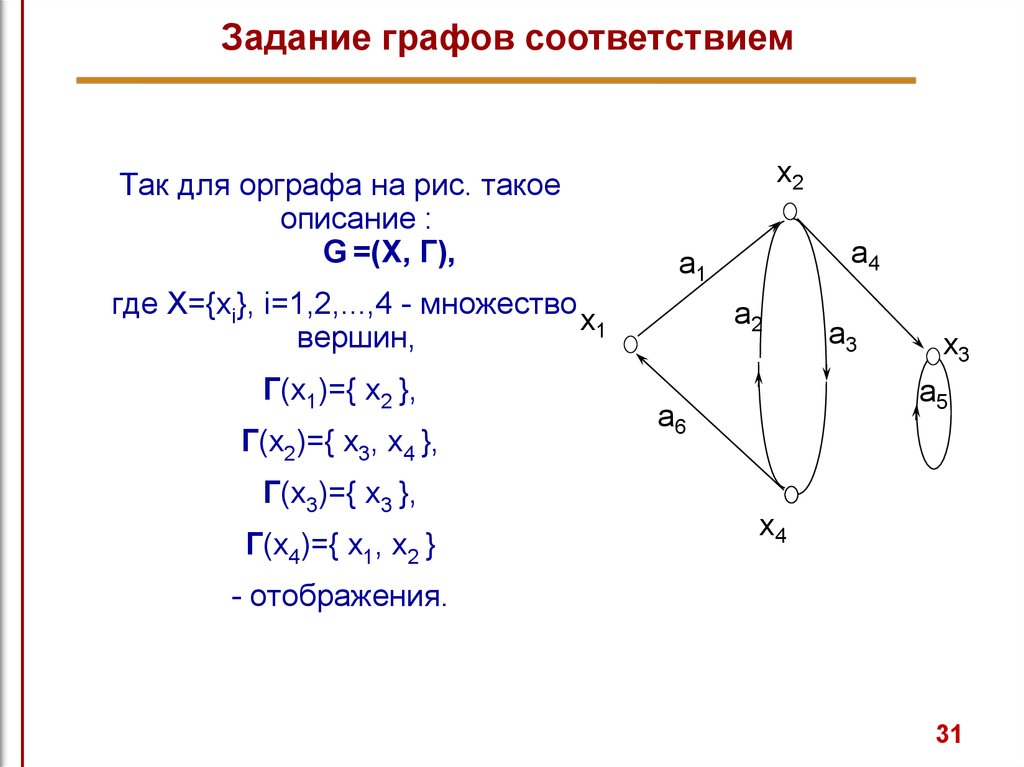
31.

Задание графов соответствием
Так для орграфа на рис. такое
описание :
G =(X, Г),
x2
где X={xi}, i=1,2,...,4 - множество
x1
вершин,
Г(х1)={ x2 },
Г(x2)={ x3, x4 },
Г(x3)={ x3 },
Г(x4)={ x1, x2 }
a4
a1
a2
a3
x3
a5
a6
x4
- отображения.
31

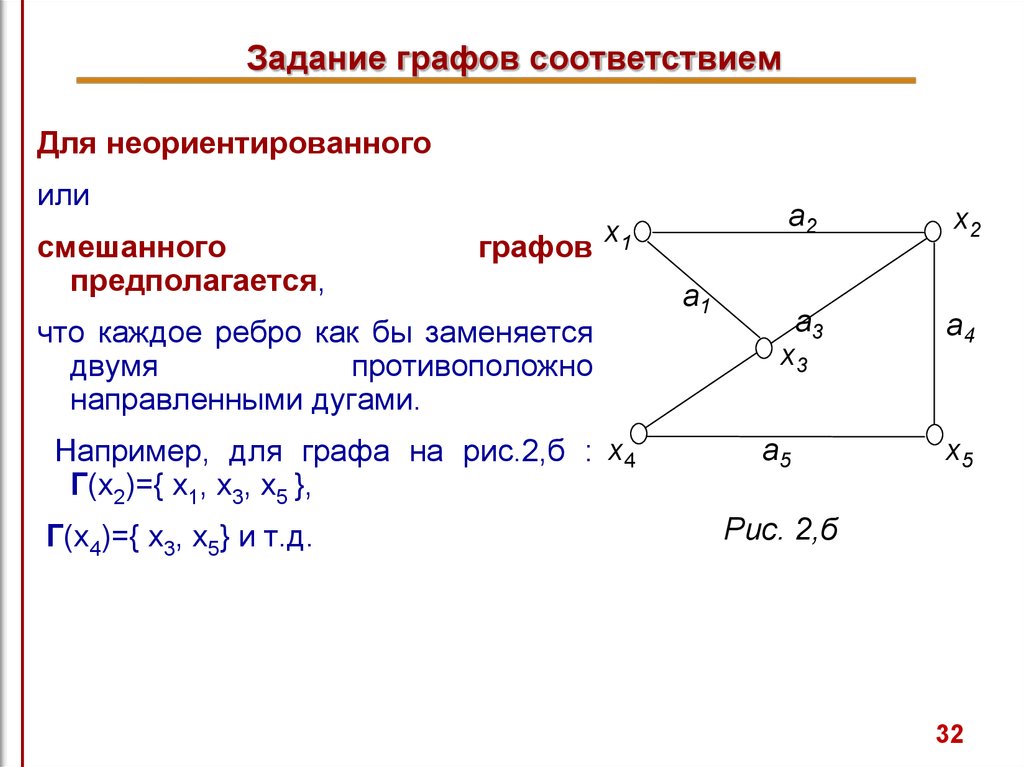
32. Задание графов соответствием

Для неориентированного
или
смешанного
предполагается,
графов x1
что каждое ребро как бы заменяется
двумя
противоположно
направленными дугами.
Например, для графа на рис.2,б : x4
Г(х2)={ x1, x3, x5 },
Г(x4)={ x3, x5} и т.д.
a1
a2
x2
a3
x3
a4
a5
x5
Рис. 2,б
32

33. Матричное представление графов

Для обработки на ЭВМ графы удобно представлять
в виде матриц смежности и инциденций.
Матрица смежности
размерностью n n,
-
это
квадратная
матрица
где n - число вершин графа, однозначно представляющая
его структуру.
A={aij}, i,j= 1,2,...,n, причем
aij=1, если дуга (xi, xj),
aij=0, если нет дуги (xi, xj).
33

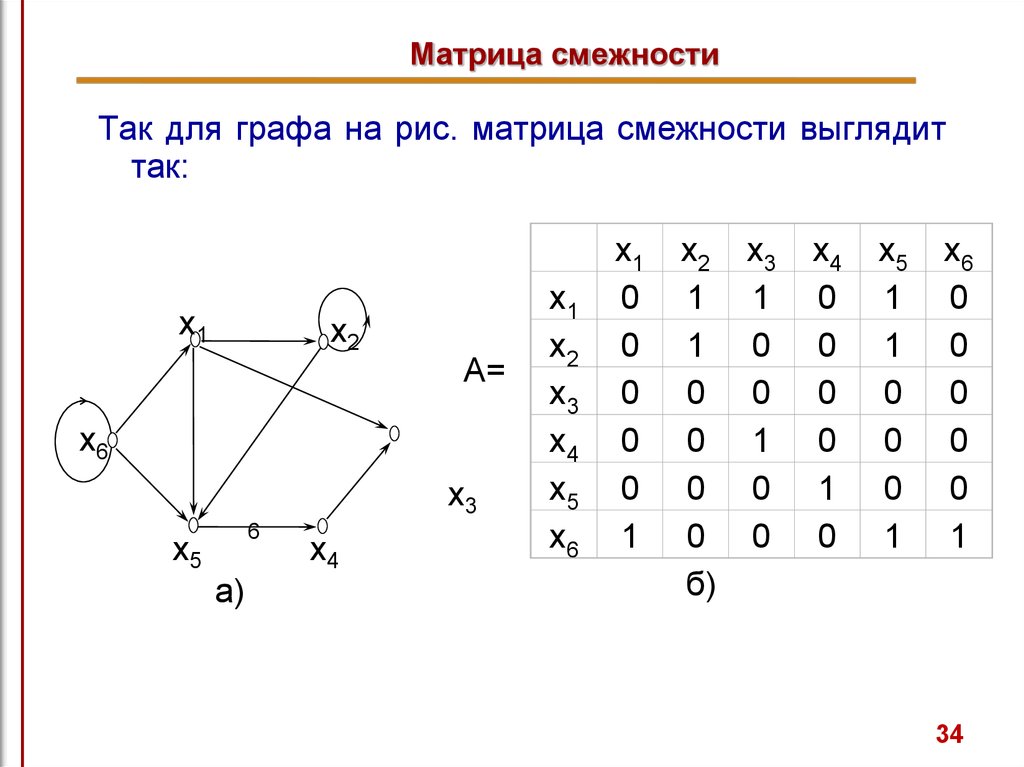
34. Матрица смежности

Так для графа на рис. матрица смежности выглядит
так:
x1
x2
А=
x6
x3
x5
6
а)
x4
x1
x2
x3
x4
x5
x6
x1
0
0
0
0
0
1
x2 x3
1 1
1 0
0 0
0 1
0 0
0 0
б)
x4
0
0
0
0
1
0
x5
1
1
0
0
0
1
x6
0
0
0
0
0
1
34

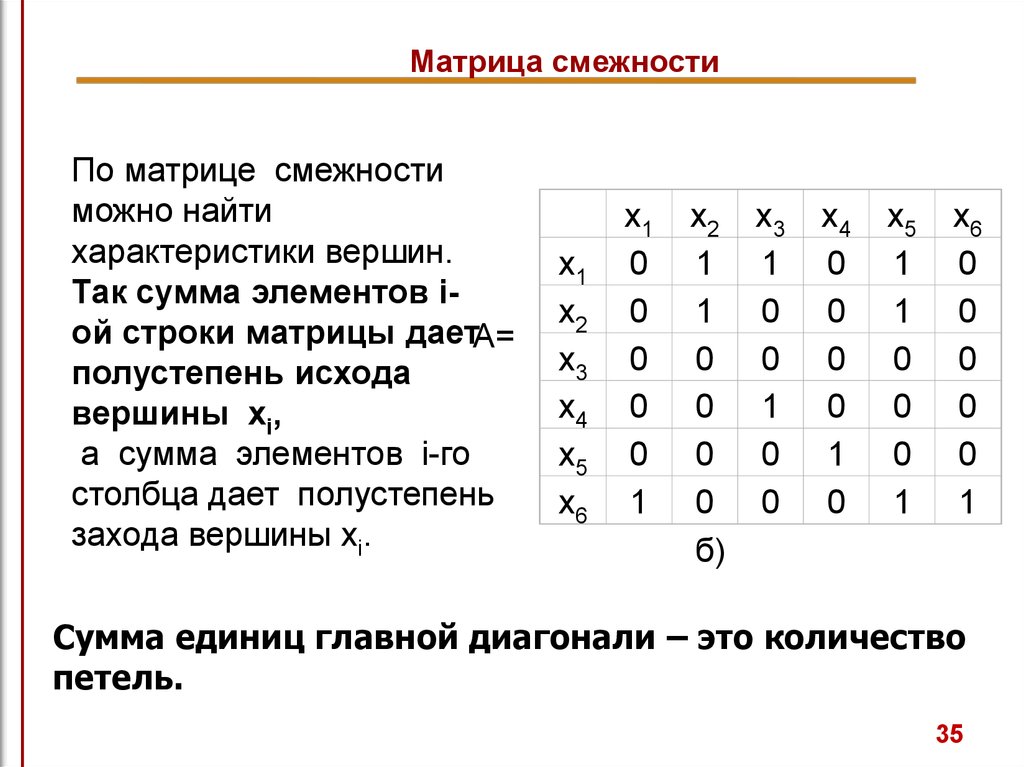
35.

Матрица смежности
По матрице смежности
можно найти
характеристики вершин.
Так сумма элементов iой строки матрицы даетА=
полустепень исхода
вершины xi,
а сумма элементов i-го
столбца дает полустепень
захода вершины xi.
x1
x2
x3
x4
x5
x6
x1
0
0
0
0
0
1
x2 x 3
1 1
1 0
0 0
0 1
0 0
0 0
б)
x4
0
0
0
0
1
0
x5
1
1
0
0
0
1
x6
0
0
0
0
0
1
Сумма единиц главной диагонали – это количество
петель.
35

36. Матрица смежности

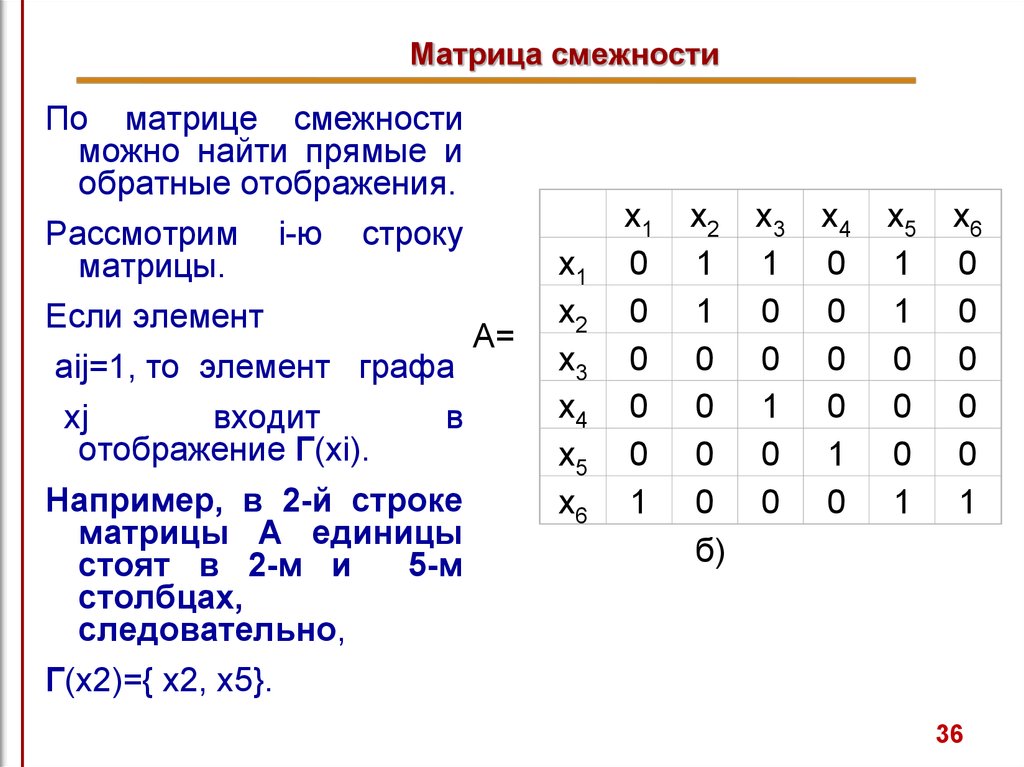
По матрице смежности
можно найти прямые и
обратные отображения.
Рассмотрим i-ю строку
матрицы.
Если элемент
А=
aij=1, то элемент графа
xj
входит
в
отображение Г(xi).
Например, в 2-й строке
матрицы А единицы
стоят в 2-м и
5-м
столбцах,
следовательно,
Г(х2)={ x2, x5}.
x1
x2
x3
x4
x5
x6
x1
0
0
0
0
0
1
x2 x 3
1 1
1 0
0 0
0 1
0 0
0 0
б)
x4
0
0
0
0
1
0
x5
1
1
0
0
0
1
x6
0
0
0
0
0
1
36

37.

Матрица инциденций
Матрица инциденций - это прямоугольная матрица размером
n m,
где n- количество вершин графа, а m - количество дуг графа.
Обозначается матрица инциденций
B={ bij },i=1,2,...,n, j=1,2,...,m.
Каждый элемент матрицы :
bij= 1, если xi является начальной вершиной дуги aj,
bij= -1, если xi является конечной вершиной дуги aj,
bij= 0, если xi не является концевой вершиной дуги aj или если
aj является петлей.
37

38.

Матрица инциденций
x 1 a1
a3
x2
a9
a8 a4
a10 x6
x3
a5
a7
x5
В=
a2
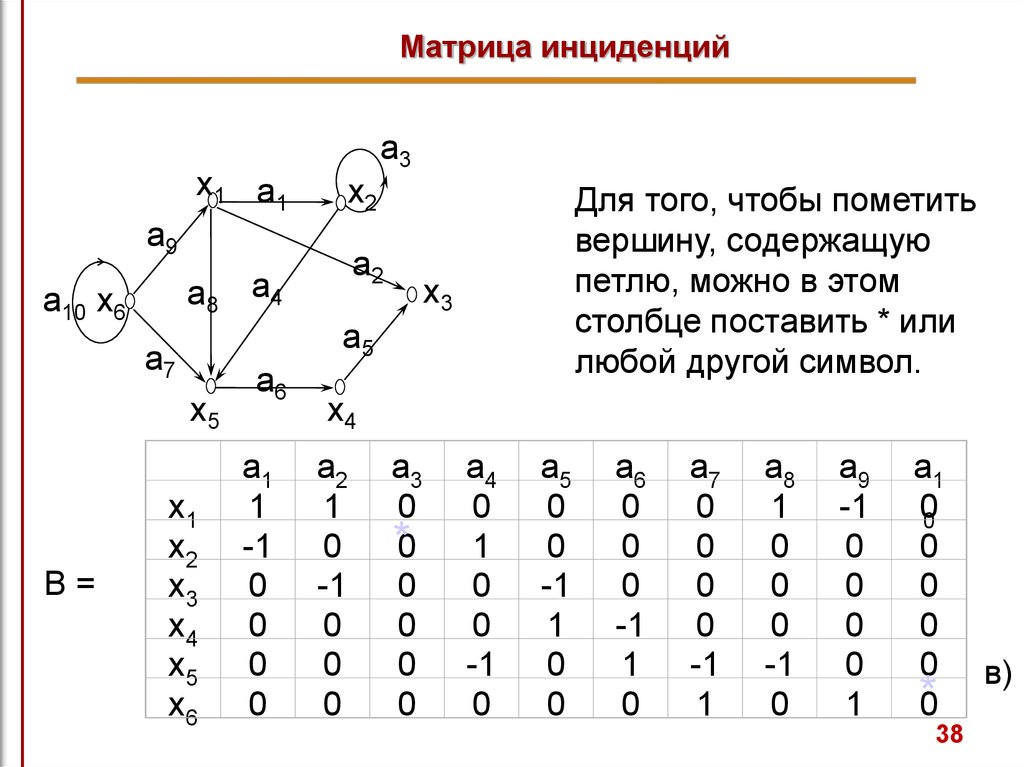
Для того, чтобы пометить
вершину, содержащую
петлю, можно в этом
столбце поставить * или
любой другой символ.
x1
x2
x3
x4
x5
x6
a6
a1
1
-1
0
0
0
0
x4
a2
1
0
-1
0
0
0
a3
0
*0
0
0
0
0
a4
0
1
0
0
-1
0
a5
0
0
-1
1
0
0
a6
0
0
0
-1
1
0
a7
0
0
0
0
-1
1
a8
1
0
0
0
-1
0
a9
-1
0
0
0
0
1
a1
00
0
0
0
0
*0
38
в)

39.

Матрица инциденций
По матрице инциденций можно найти характеристики графа:
Число 1 в i-ой строке– это d0(xi)
*
Число -1 в i-ой строке– это dt(xi)
*
Число нулевых столбцов – это число петель в графе.
В=
x1
x2
x3
x4
x5
x6
a1
1
-1
0
0
0
0
a2
1
0
-1
0
0
0
a3
0
0
*
0
0
0
0
a4
0
1
0
0
-1
0
a5
0
0
-1
1
0
0
a6
0
0
0
-1
1
0
a7
0
0
0
0
-1
1
a8
1
0
0
0
-1
0
a9
-1
0
0
0
0
1
a1
00
0
0
0
0
*0 39

40.

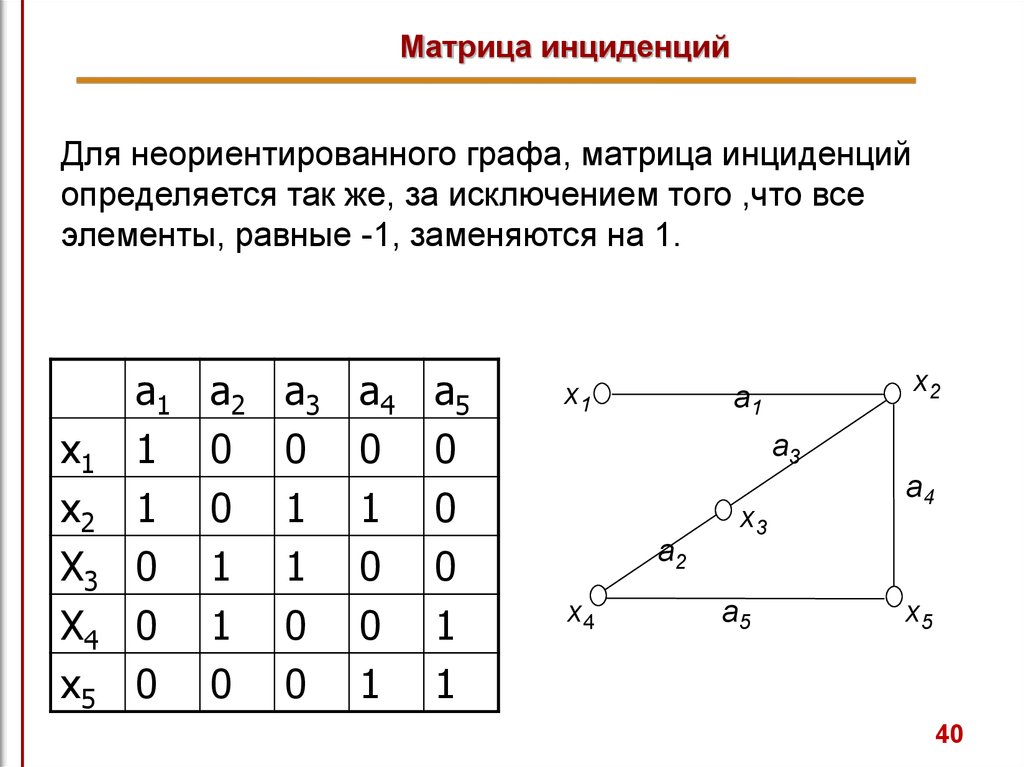
Матрица инциденций
Для неориентированного графа, матрица инциденций
определяется так же, за исключением того ,что все
элементы, равные -1, заменяются на 1.
x1
x2
X3
X4
x5
a1
1
1
0
0
0
a2
0
0
1
1
0
a3
0
1
1
0
0
a4
0
1
0
0
1
a5
0
0
0
1
1
x1
x2
a1
a3
a2
x4
x3
a5
a4
x5
40

41. Операции над графами

Рассмотрим семь операций над графами,
три из которых являются бинарными, включающими два графа,
а остальные четыре - унарные, то есть определены на одном
графе.
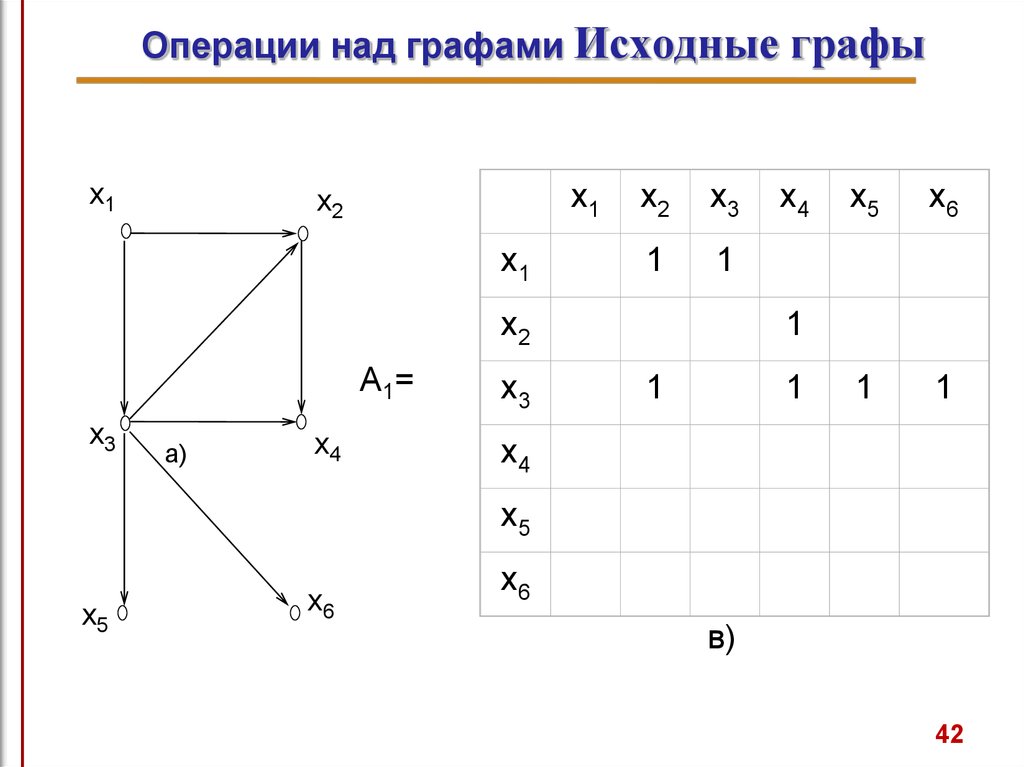
Исходные графы G1 и G2 показаны на рис. 6, а,б. G1=(X1, A1),
где X1={xi}, i=1,2,...,6, A={ ai }, i=1,2,...,7. и G2=(X2, A2), где X2={ xi },
i=1,2,...,6, A={a1, a3, a5, a6, a9, a10}.
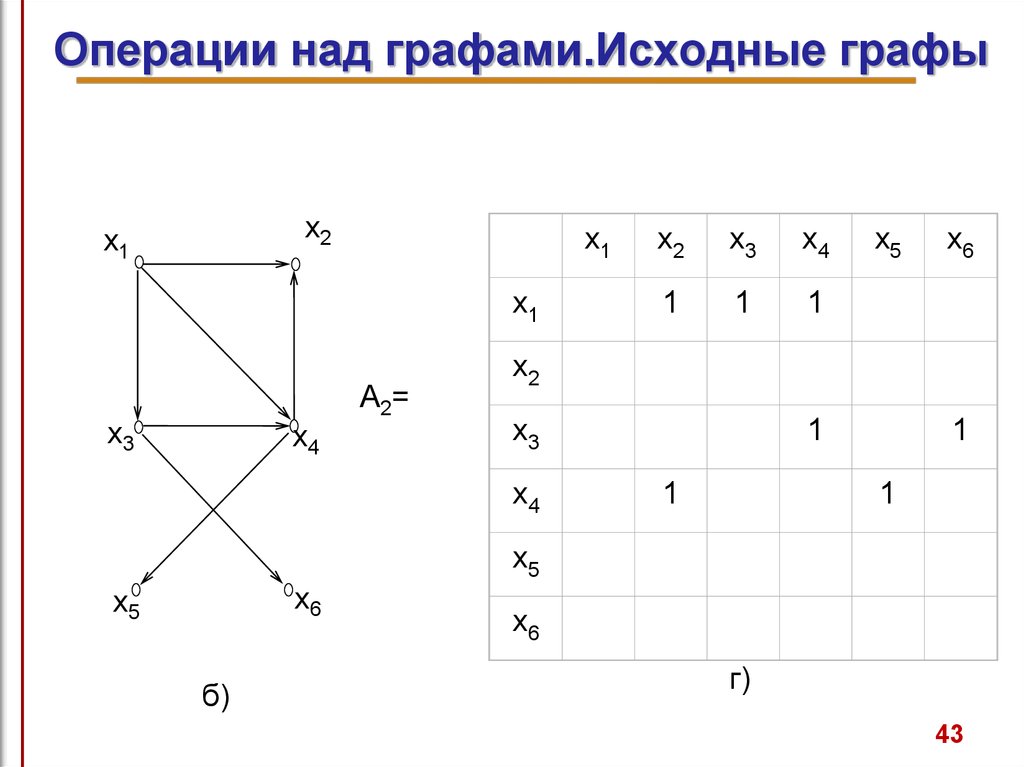
Матрицы смежности графов показаны на рис.6,в
и
6,г
соответственно. (Чтобы не загромождать рисунок , нули не
показаны).
41

42. Операции над графами Исходные графы

Операции над графами Исходные
x1
x1
x2
x1
x2
x3
1
1
x2
А1=
x3
а)
x4
x3
графы
x4
x5
x6
1
1
1
1
1
x4
x5
x5
x6
x6
в)
42

43. Операции над графами.Исходные графы

x2
x1
x1
x1
А2=
x3
x4
x2
x3
x4
1
1
1
x5
x6
x2
x3
x4
1
1
1
1
x5
x6
x5
б)
x6
г)
43

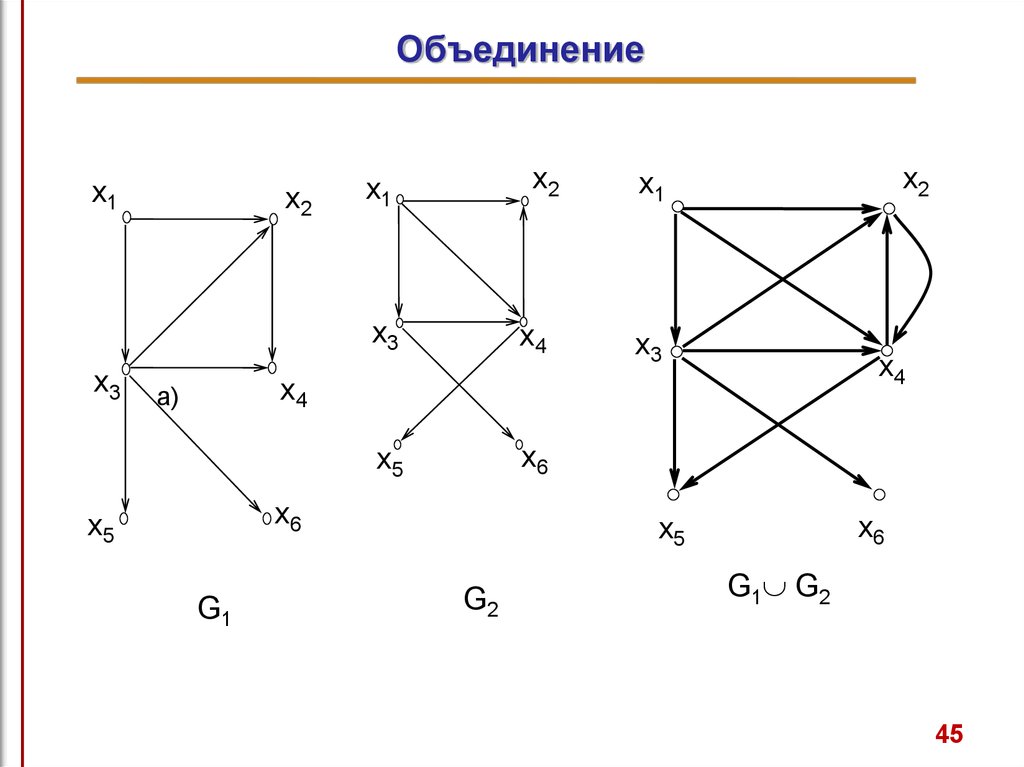
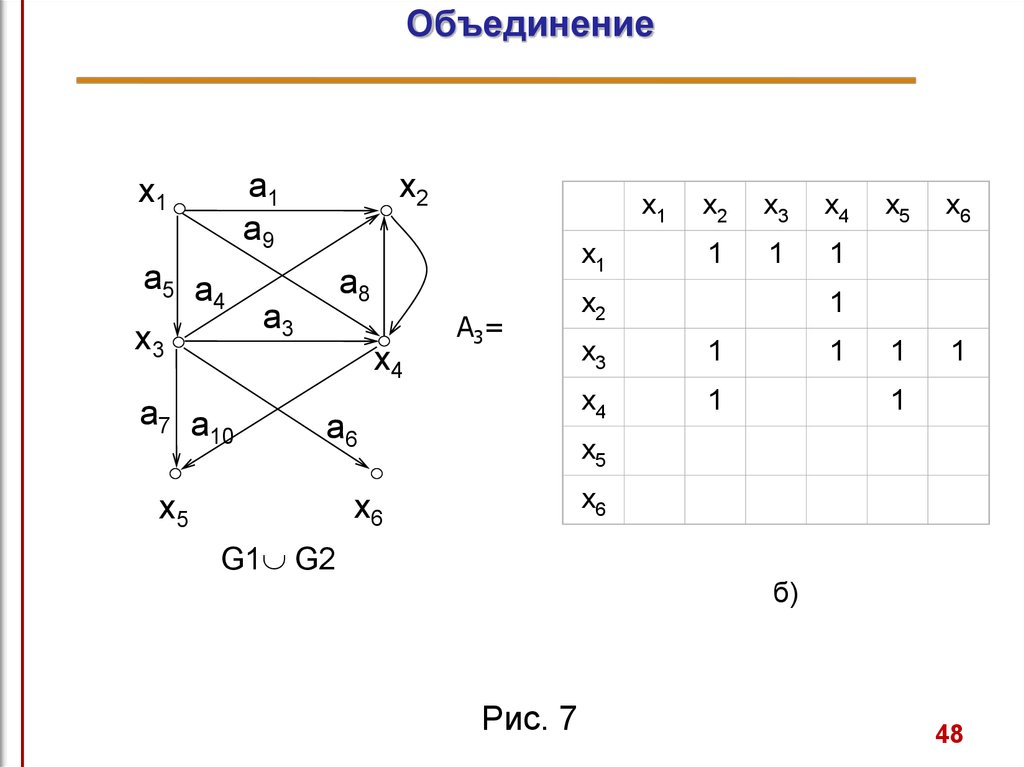
44. Операции над графами. Объединение

Объединение графов G1 и G2, обозначаемое как
G 1 G 2,
представляет такой граф
G3=(X1 X2, A1 A2),
что множество его вершин является объединением Х1 и Х2,
а множество ребер - объединением А1 и А2.
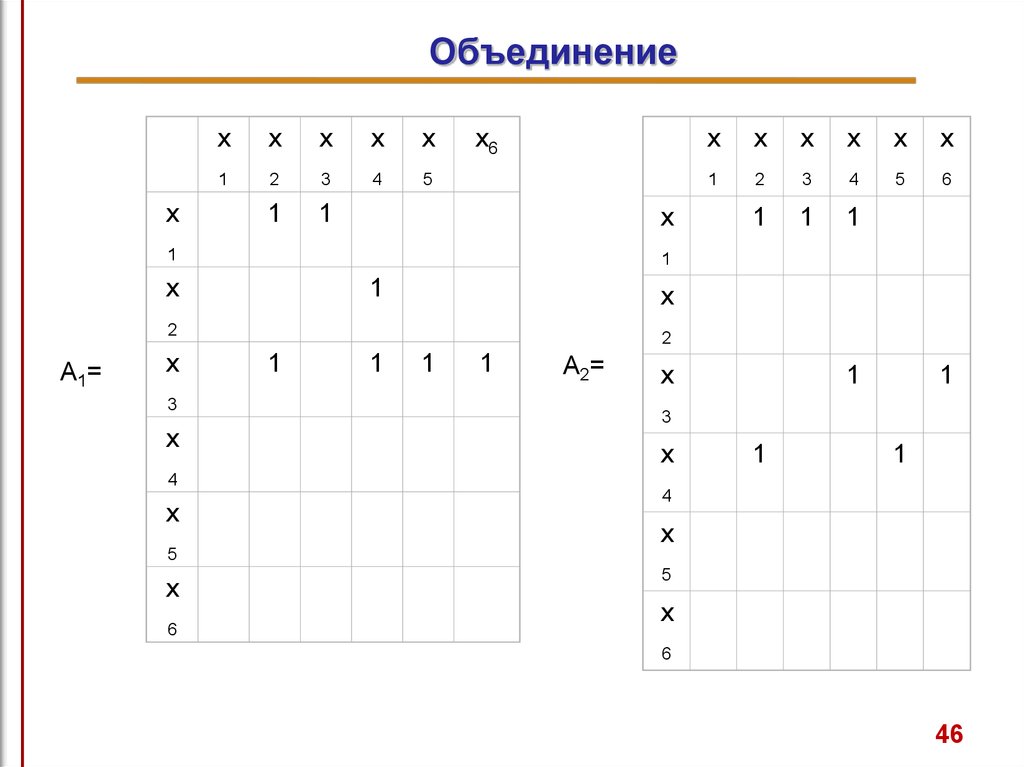
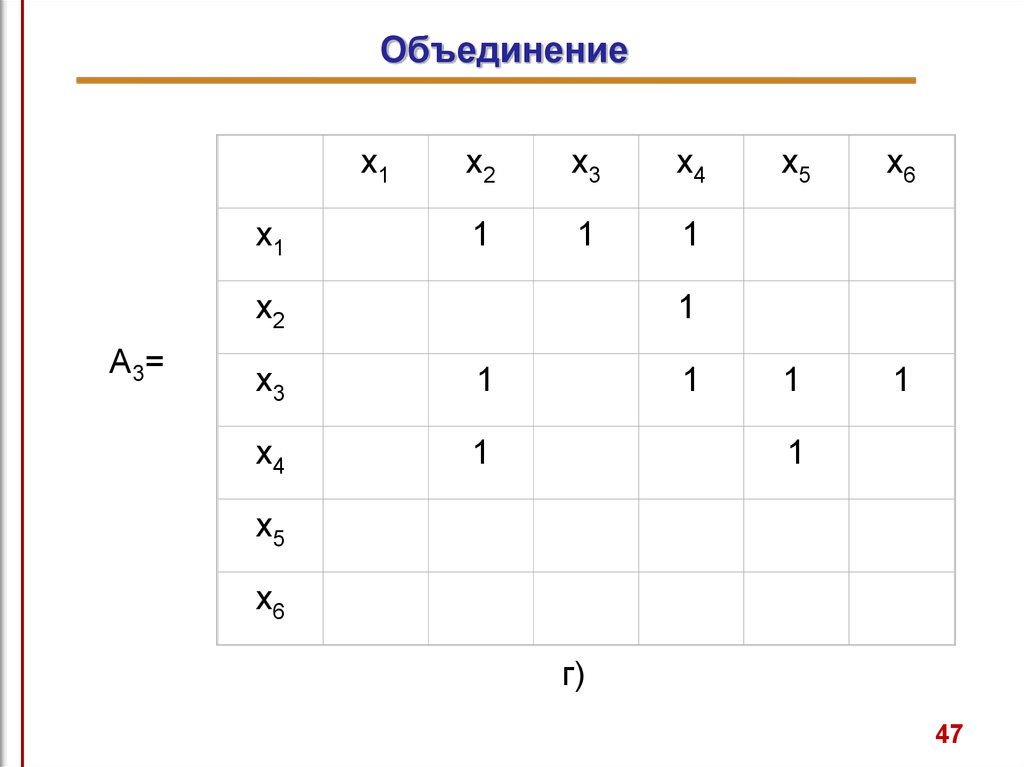
Граф G3, полученный операцией объединения графов G1 и
G2, показан на рис. 7а, а его матрица смежности - на рис. 7б.
44

45. Объединение

x1
x3
x2
x2
x1
x3
x4
x5
x6
x2
x1
x3
x4
x4
а)
x6
x5
G1
x6
x5
G2
G 1 G 2
45

46. Объединение

x
x
x
x
x
x
1
2
3
4
5
1
1
x6
x
1
1
3
x
x
x
x
x
1
2
3
4
5
6
1
1
1
x
2
x
x
1
x
А1=
x
2
1
1
1
1
А2=
x
1
1
3
x
1
1
4
x
4
x
5
x
6
5
x
6
46

47. Объединение

x1
x1
x2
x3
x4
1
1
1
x2
А3=
x5
x6
1
1
1
x3
1
x4
1
1
1
x5
x6
г)
47

48.

Объединение
a1
a9
x1
a5 a
4
x3
a7 a
10
x2
x1
x1
a8
a3
x4
А3=
a6
x3
x4
1
1
1
x5
x6
1
1
1
x2
x3
1
x4
1
1
1
x5
x6
x6
x5
x2
G1 G2
б)
Рис. 7
48

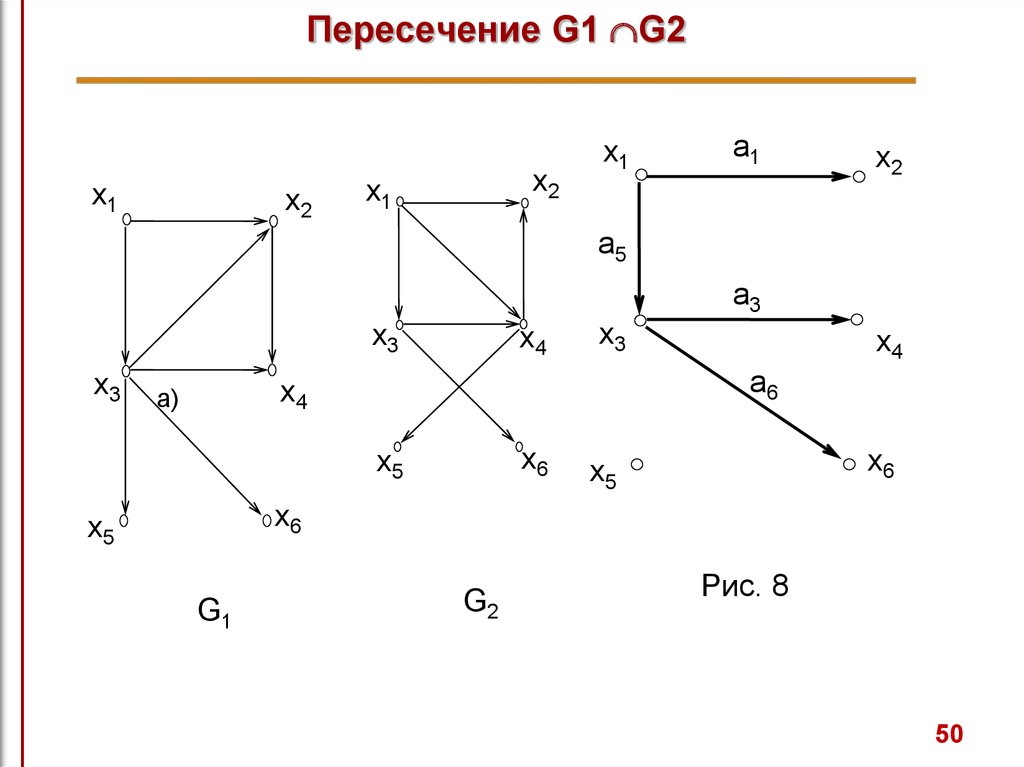
49.

Пересечение G1 G2
Пересечение графов G1 и G2, обозначаемое как
представляет собой граф
G1 G2,
G4=(X1 X2, A1 A2).
Таким образом, множество вершин графа G4 состоит из
вершин, присутствующих одновременно в G1 и G2.
Операция пересечения графов G1 G2 показана на рис. 8.
49

50. Пересечение G1 G2

Пересечение G1 G2
x1
x2
x2
x1
x1
a1
x2
a5
a3
x3
x3
x4
x3
a6
x4
а)
x4
x6
x5
x6
x5
x6
x5
G1
G2
Рис. 8
50

51. Пересечение G1 G2

Пересечение G1 G2
x
x
x
x
x
x
1
2
3
4
5
1
1
x6
x
1
1
3
x
1
3
6
2
4
5
1 1 1
x
2
x
x x x
1
x
А1=
x x
2
1
1
1
1
А2
=
x
1
1
3
x
x
4
4
x
x
5
5
x
x
6
6
1
1
51

52. Пересечение G1 G2

Пересечение G1 G2
x1
x1
А3=
x2
x3
1
1
x4
x5
x6
x2
x3
1
1
x4
x5
x6
г)
52

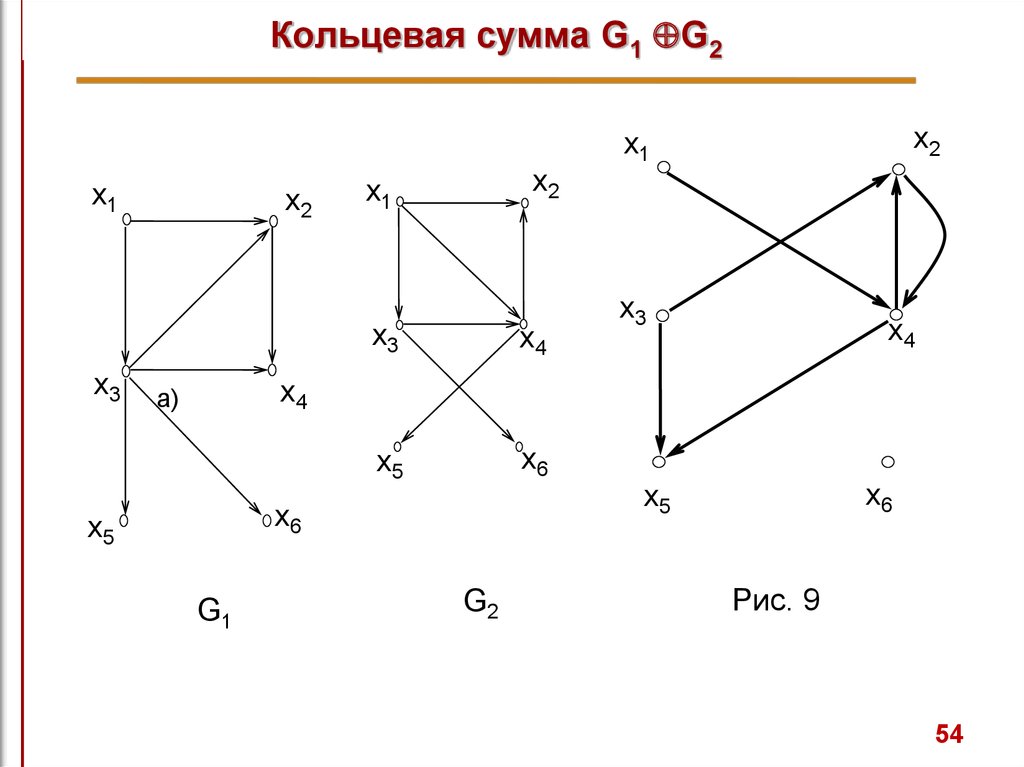
53.

Кольцевая сумма G1 G2
Кольцевая сумма двух графов G1 и G2, обозначаемая как
G1 G2,
представляет собой граф G5, порожденный на множестве
ребер
А1 А2.
Другими словами, граф G5 не имеет изолированных вершин
и состоит только из ребер, присутствующих либо в G1, либо в
G2, но не в обоих одновременно.
Кольцевая сумма графов G1 и G2 показана на рис. 9.
53

54. Кольцевая сумма G1 G2

Кольцевая сумма G1 G2
x2
x1
x1
x3
x2
x2
x1
x3
x4
x5
x6
x3
x4
x4
а)
x6
x5
G1
x6
x5
G2
Рис. 9
54

55.

Операции над графами
Три рассмотренные операции коммутативны т.е.
G1 G2 = G2 G1,
G1 G2 = G2 G1,
G1 G2 = G2 G1 ,
и многоместны ,
т.е. G1 G2 G3 G4 ... , G1 G2 G3 G4 ... и так
далее.
55

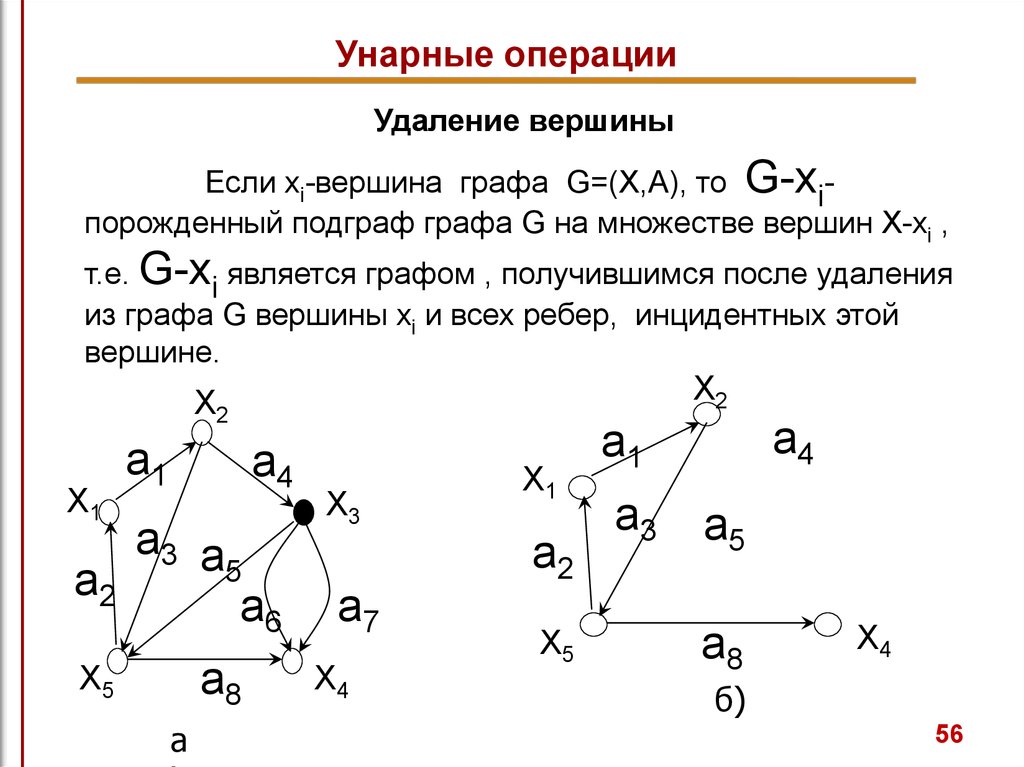
56.

Унарные операции
Удаление вершины
Если xi-вершина графа G=(X,A), то G-xiпорожденный подграф графа G на множестве вершин X-xi ,
т.е. G-xi является графом , получившимся после удаления
из графа G вершины xi и всех ребер, инцидентных этой
вершине.
X2
X2
X1
a1
a4
a3 a
5
a2
a6
a8
X5
а
X3
X1
a2
a7
X4
X5
a4
a1
a3
a5
a8
X4
б)
56

57.

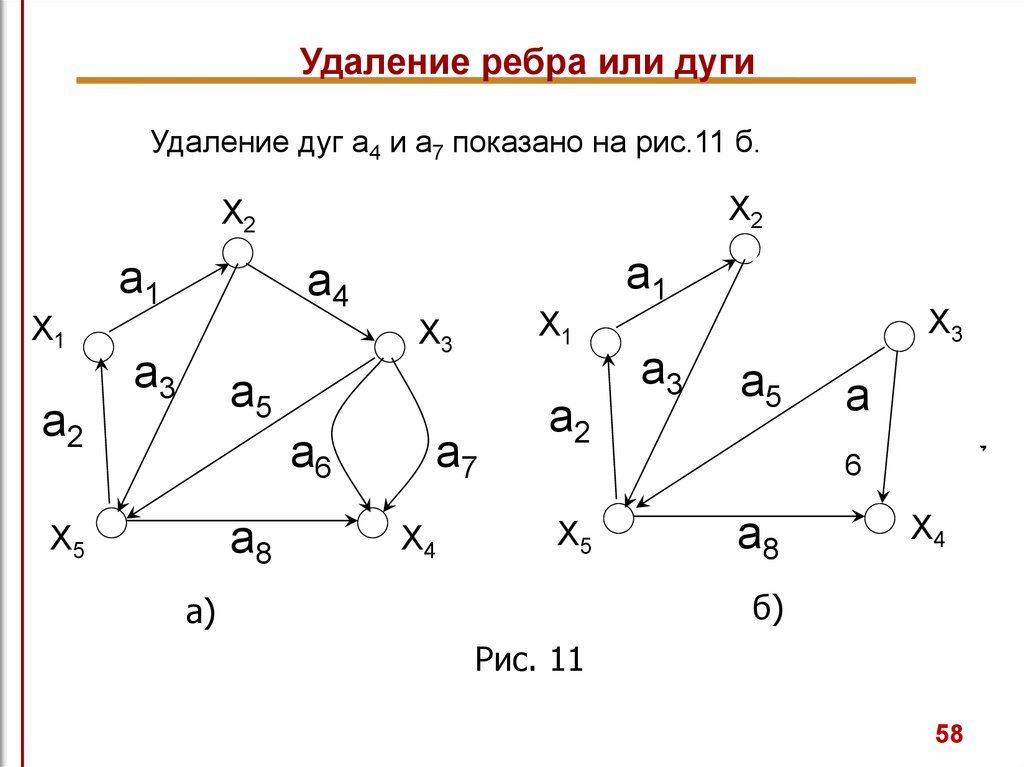
Удаление ребра или дуги
Если ai-дуга графа G=(X,A), то
G-ai
- подграф графа G, получающийся после удаления
из G дуги ai.
Заметим, что концевые вершины дуги ai не удаляются.
Удаление из графа множества вершин или дуг
определяются как
последовательное
удаление
определенных вершин или дуг.
57

58.

Удаление ребра или дуги
Удаление дуг a4 и a7 показано на рис.11 б.
X2
X2
a1
X1
a2
a5
a6
a8
X5
a7
X4
X3
X1
X3
a3
a4
a1
a4
a2
X5
a3
a5
а
a6 6
a8
a7
X4
б)
а)
Рис. 11
58

59.

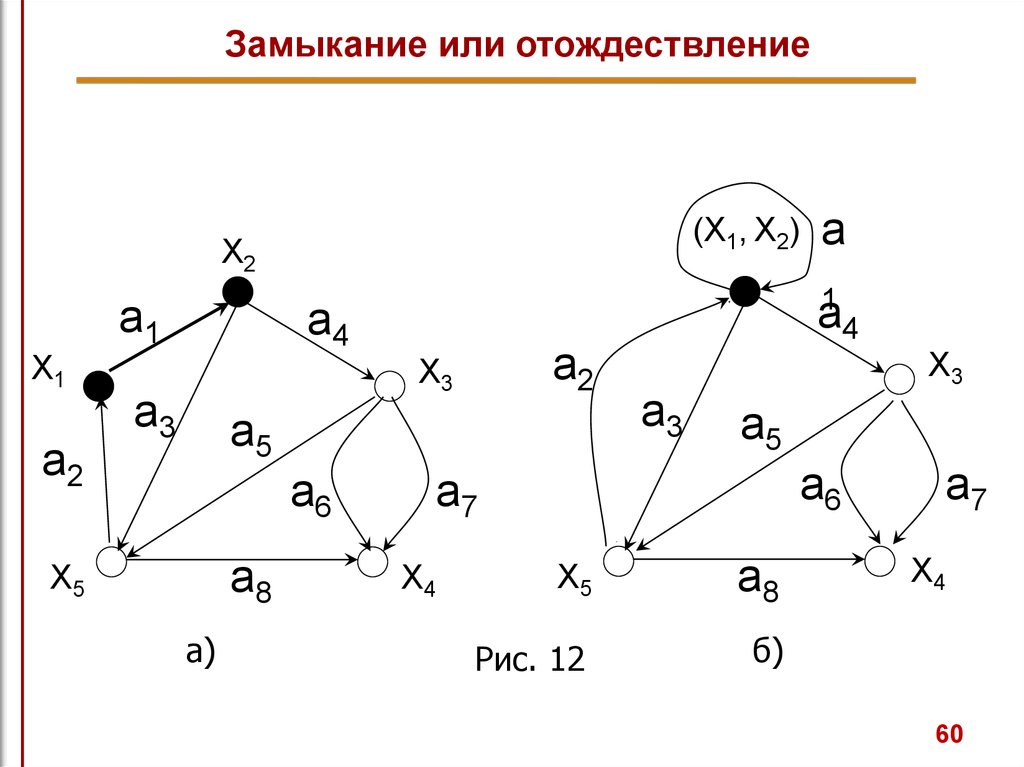
Замыкание или отождествление
Говорят, что пара вершин xi и xj в
графе G замыкается (или
отождествляется),
если они заменяются такой новой
вершиной, что все дуги в графе G,
инцидентные вершинам xi и xj ,
становятся инцидентными новой
вершине.
59

60.

Замыкание или отождествление
(X1, Х2)
X2
X2
a1
a4
X1
a2
Xa
12
X3
a3
a5
a6
a8
X5
а)
a7
X4
a2
a
a1 4
a1
X3
a3
a5
a6
X5
a8
Рис. 12
б)
a7
X4
60

61.

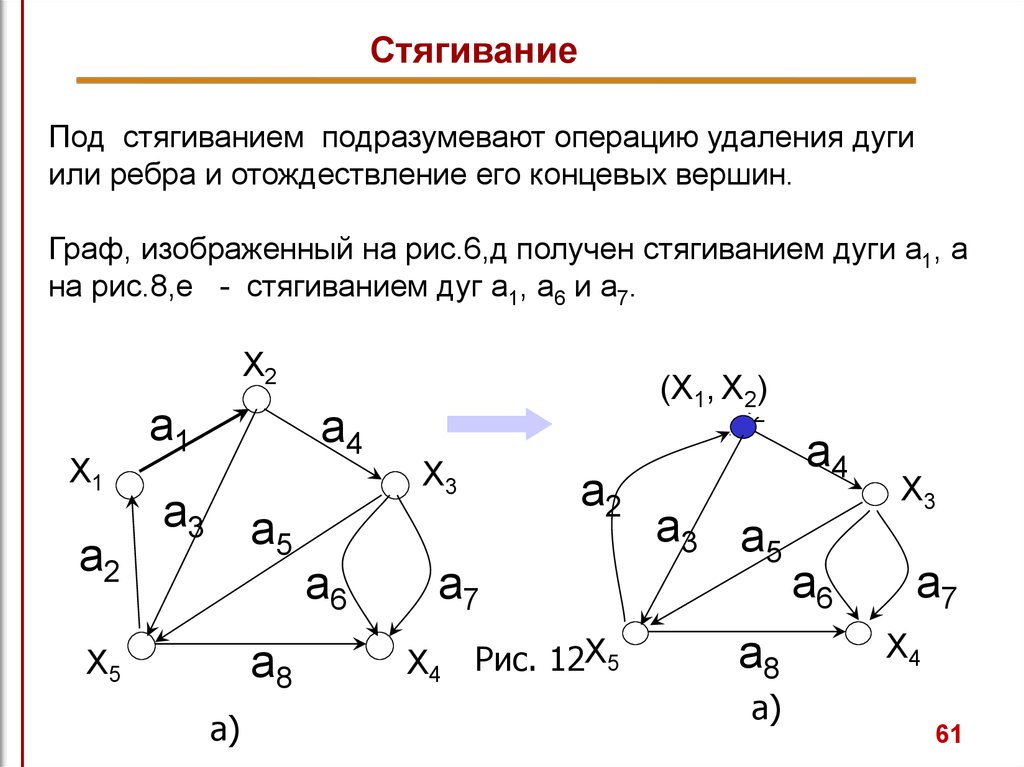
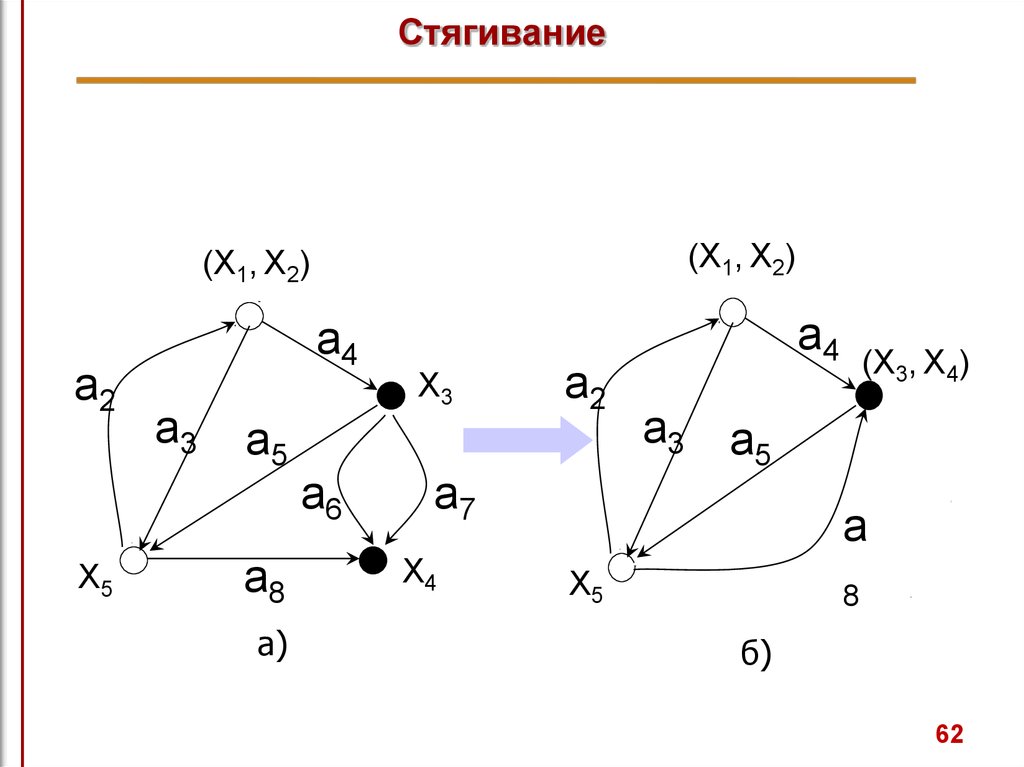
Стягивание
Под стягиванием подразумевают операцию удаления дуги
или ребра и отождествление его концевых вершин.
Граф, изображенный на рис.6,д получен стягиванием дуги а1, а
на рис.8,е - стягиванием дуг a1, a6 и a7.
X2
a1
X1
a2
(X1, ХX2)
2
a4
X3
a3
a5
a6
a8
X5
а)
a7
Xa1 2
a2
X4 Рис. 12X5
a4
a1
a3 a5
a8
а)
a6
X3
a7
X4
61

62. Стягивание

(X1, Х2)
X2
(X1, Х2)
X2
Xa1 2
a2
X5
a4
a1
a3
X3
a5
a6
a8
а)
a7
X4
Xa1 2
a2
X5
a4
a1
(X3, Х4)
X3
a3 a
5
a6
a8
а
8
a7
X4
б)
62