Похожие презентации:
Решение задач ЛП методом симплекс - таблиц
1. 5.5.4. Решение задач ЛП методом симплекс - таблиц
2.
Требуется найти максимальноезначение целевой функции
f ( x) c1 x1 c2 x2 cn xn
при ограничениях
a1,m 1 xm 1 a1n xn b1 ,
x1
x2 a2,m 1 xm 1 a2 n x n b2 ,
(5.14)
xm am,m 1 xm 1 amn xn bm ,
x 0, j 1,m.
j
3.
Предполагается, что bi 0, i 1, m .Запишем систему (5.14) в векторной
форме
A1 x1 A2 x2 Am xm Am 1 xm 1 An xn A0 , (5.15)
где
a1,m 1
a1n
b1
1
0
0
a
b
0
1
0
a2,m 1
A1 , A2 , , Am , Am 1
, , An 2 n , A0 2 .
a
0
0
1
b
a
m
mn
m,m 1
4.
Векторы A1 , A2 , , Am являютсялинейно независимыми единичными
векторами m - мерного пространства и
образуют базис этого пространства.
Соответствующие этим векторам
переменные x1 , x 2 , , x m принимаем за
базисные переменные. Остальные
переменные xm 1 , xm 2 , , xn считаются
свободными или небазисными.
5.
Базисные переменные входят в целевуюфункцию с нулевыми коэффициентами.
f ( x) c1 x1 c 2 x2 cm xm сm 1 xm 1 cm 2 xm 2 c n xn ,
c1 c2 cm 0.
Введем в рассмотрение вектор коэффициентов
целевой функции при базисных переменных
cB (cB1, cB2 , , cBm ) (c1, c2 , , cm ).
Для исследования плана на оптимальность
построим начальную симплекс-таблицу.
6.
7.
Заполнение таблицы. В первом столбцетаблицы записываются базисные переменные
xi (i 1, m) и перед ними коэффициенты c Bi
целевой функции при текущих базисных
переменных, записанных в том же порядке.
В верхней части таблицы располагаются
небазисные переменные x j ( j m 1, n) и
коэффициенты целевой функции c j , с
которыми эти переменные входят в целевую
функцию.
8.
В столбце x j ( j m 1, n) записываютсякоэффициенты разложения вектора А j
по базису (5.15).
Крайний справа столбец заполняется
элементами столбца А0 в разложении
(5.15), в нем же в результате вычислений
получаем оптимальный план.
9.
Заполнение f – строки. В f - строкезаписываются относительные оценки
j ( j m 1, n) , характеризующие прирост
целевой функции при включении в базис
небазисной переменной x j и Q значение целевой функции, для текущих
базисных переменных
j (CВ , Aj ) c j , j m 1, n , Q (CВ , A0 ) ,
здесь (C В , A j ) - скалярное произведение
соответствующих векторов.
10.
Для оптимальности опорного решения взадаче на максимум требуется
выполнение неотрицательности всех
относительных оценок j 0 . Если все
оценки положительны, то расчет закончен
и в последнем столбце таблицы А0
находятся оптимальные значения
базисных переменных. Если хотя бы одна
оценка отрицательна, то можно улучшить
полученное решение.
11.
Улучшение полученного решения.Улучшение достигается путем
составления новых таблиц с помощью
процедуры повторяющихся расчетов –
итераций до тех пор, пока не будет
получено оптимальное решение задачи,
либо сделан вывод о неразрешимости
поставленной задачи. Итерационный
процесс состоит из трех шагов.
12.
1. Найти переменную длявключения в базис.
Выберем наибольшую по модулю
отрицательную оценку s .
Соответствующая переменная x s
включается в базис. Все элементы над
выбранной оценкой образуют
разрешающий столбец.
13.
2. Найти переменную для исключенияиз базиса.
Для этого составим отношение
свободных членов к соответствующим
положительным элементам
разрешающего столбца. В той строке, где
достигается минимум, соответствующая
переменная xr исключается из базиса.
Эта строка называется разрешающей
строкой.
14.
Число a rs находящееся напересечении разрешающей строки и
разрешающего столбца называется
разрешающим элементом.
3. Построить новую симплекстаблицу.
Построение новой симплекс-таблицы
состоит из следующих шагов.
15.
• переменные xr и x s меняютсяместами;
• разрешающий элемент a rs
заменяется на обратный
1
'
ars
;
ars
• элементы разрешающей строки
делятся на разрешающий элемент;
• элементы разрешающего столбца
делятся на разрешающий элемент и
меняют знак;
16.
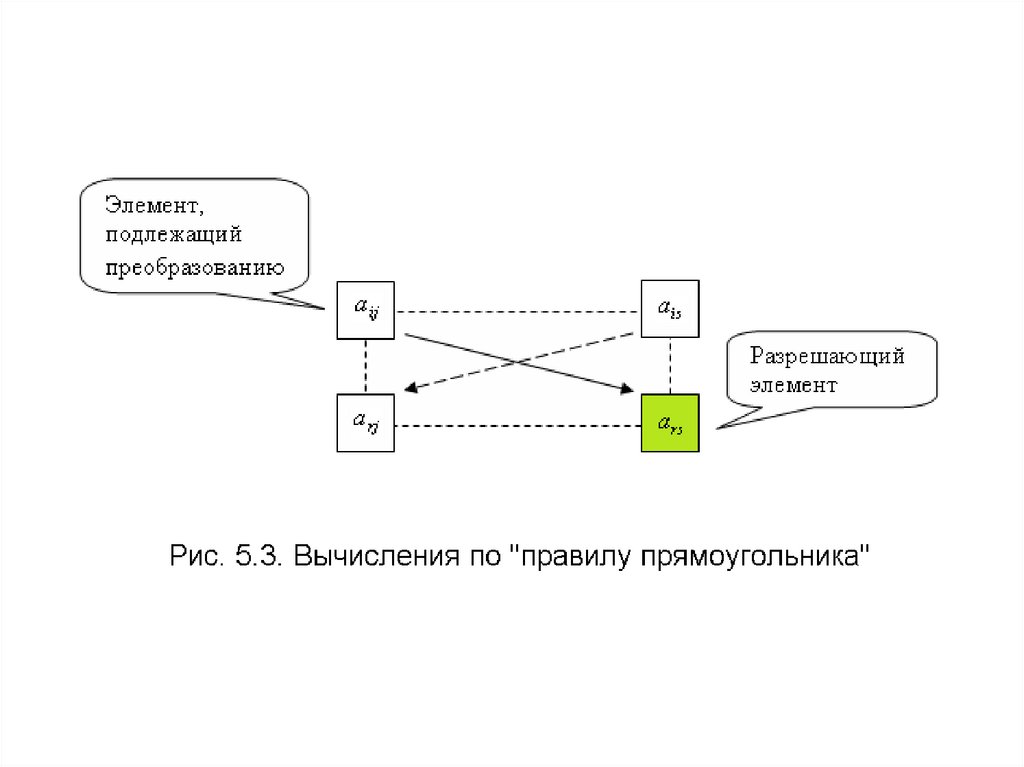
остальные элементы пересчитываютсяпо «правилу прямоугольника».
Находится разность произведений
элементов, стоящих в противоположных
вершинах прямоугольника (рис.5.3)
деленная на разрешающий элемент
aij
aij ars ais arj
ars
где aij - рассчитываемый элемент новой
симплекс-таблицы
17.
18.
Пример 5.4. Предприятие может работать подвум технологическим процессам, причем за
единицу времени по 1-й технологии выпускает 260
изделий, по 2-й – 300 изделий. В таблице
указаны затраты каждого ресурса в единицу
времени.
19.
Найти программу максимального выпускапродукции из имеющихся ресурсов.
Математическая модель
Обозначим через x1, x2 - количество единиц
времени необходимое для выпуска продукции
по первому и второму технологическому
процессу соответственно.
Тогда задача заключается в следующем:
максимизировать целевую функцию
f ( x) 260x1 300x2
20.
при ограничениях16 x1 12 x2 1200
0,2 x 0,4 x 30
1
2
6 x1 5 x2 600
3 x
4 x2 300
1
x1 , x2 0
Приведем задачу к канонической форме. Для
этого в левые части ограничений вводим
дополнительные переменные. Эти
переменные выбираются так, чтобы они
обращали неравенства в равенства.
x3 0, x4 0, x5 0, x6 0 .
21.
16 x1 12 x2 x31200
0,2 x 0,4 x x
30
1
2
4
6 x1 5 x2 x5 600
x6 300
3x1 4 x2
x j 0, j 1,6
(5.16)
f ( x) 260 x1 300 x2 0 x3 0 x4 0 x5 0 x6 (5.17)
22.
Физически xi , i 1,6означают
остатки ресурсов не использованные в
производстве.
а) построение начальной симплекстаблицы
Запишем систему (5.16) в векторной
форме:
23.
A1 x1 A2 x2 A3 x3 A4 x4 A5 x5 A6 x6 A0 , (5.18)16
12
1
0
0
0
1200
0,2
0,4
0
1
0
0
30
A1 , A2 , A3 , A4 , A5 , A6 , A0
.
6
5
0
0
1
0
600
3
4
0
0
0
1
300
24.
Векторы A3 , A4 , A5 , A6являются
линейно независимыми единичными
векторами 4-х мерного пространства и
образуют базис этого пространства.
Поэтому в разложении (5.18) за
базисные переменные выбираем
переменные x3 , x4 , x5 , x6 . Небазисными
переменными являются x1, x2 .
25.
Разложение (5.18) позволяет найтипервое базисное допустимое решение.
Для этого свободные переменные x1 , x2
приравниваем нулю. В результате
получим разложение
A3 x3 A4 x4 A5 x5 A6 x6 A0 ,
которому соответствует первоначальный
опорный план
x0 ( x1 , x2 , x3 , x4 , x 5 , x6 )
(0, 0, 1200, 30, 600, 300), f ( x0 ) 0.
26.
Для проверки плана x 0 наоптимальность построим первую
симплекс-таблицу.
Введем в рассмотрение вектор
коэффициентов целевой функции при
базисных переменных
CB (с3 , с4 , с5 , с6 ) (0, 0, 0, 0) .
Т
Т
27.
Заполнение таблицы.28.
Заполнение f – строки. Найдемотносительные оценки 1 , 2 и Q
значение целевой функции .
1 (CB A1 ) c1
0 16 0 0,2 0 6 0 3 260 260;
2 (CB A2 ) c2
0 12 0 0,4 0 5 0 4 300 300;
Q (C B A0 ) 0 1200 0 30 0 600 0 300 0.
29.
30.
Для оптимальности опорного решения взадаче на максимум требуется
выполнение неотрицательности всех
относительных оценок j 0 .
Так как оценки 1 260 и 2 300 в
f - строке отрицательны, то это
свидетельствуют о возможности
улучшения полученного решения.
31.
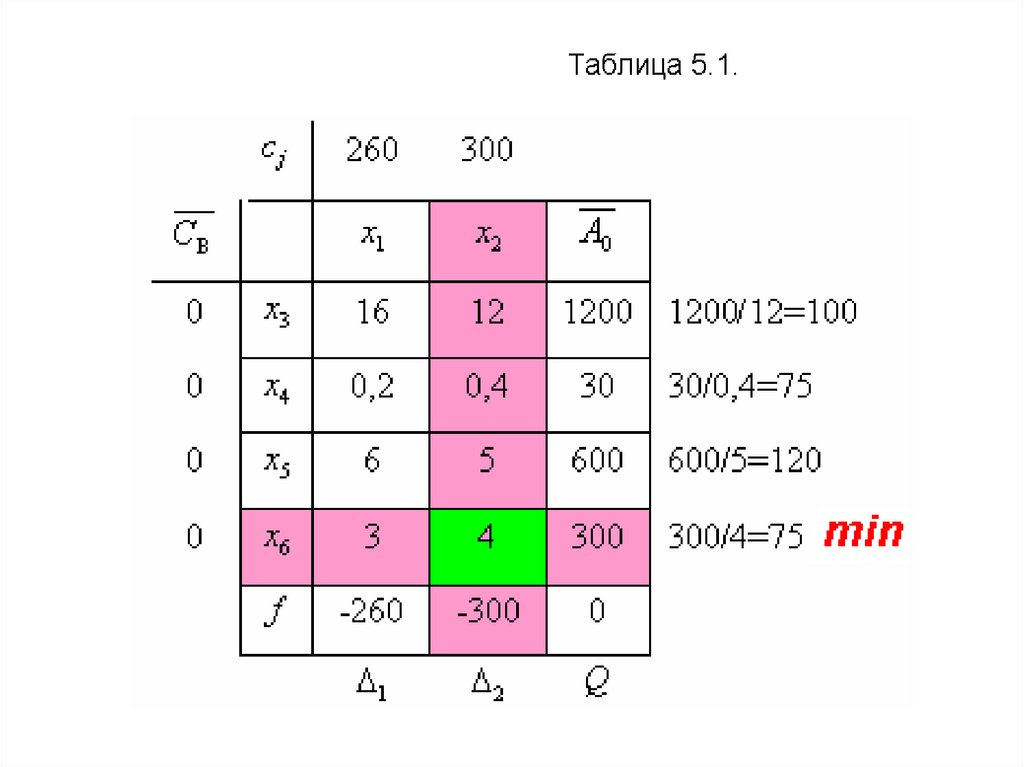
Улучшение полученного решения.Наибольшая по модулю отрицательная
оценка 2 300 . В базис будет включена
соответствующая ей небазисная
переменная x2 . Составим отношения
свободных членов к положительным
элементам разрешающего столбца.
Данные отношения приведены справа от
таблицы.
32.
Наименьшему частномуmin(100, 75, 120, 75)=75
соответствует строка с переменной x6 .
Эта переменная исключается из базиса.
В табл.5.1 разрешающий столбец и
разрешающая строка выделены другим
цветом. Разрешающим элементом является
число a42 4 .
Построим новую симплекс-таблицу.
Ниже поэтапно демонстрируется процесс
заполнения новой симплекс - таблицы.
33.
34.
В табл. 5.2 переменные x 2 и x 6меняются местами вместе с
коэффициентами c j . Здесь же
разрешающий элемент заменяется на
обратный.
В табл. 5.3 элементы разрешающей
строки делятся на разрешающий элемент.
Элементы разрешающего столбца
делятся на разрешающий элемент и
меняют знак.
35.
Остальные элементы (табл. 5.4)рассчитываются по «правилу
прямоугольника»
16 4 3 12
a
7;
4
0,2 4 3 0,4
a
0,1;
4
6 4 3 5
a
2,25;
4
1200 4 300 12
a
300;
4
30 4 300 0,4
a
0;
4
600 4 300 5
a
225;
4
'
11
'
31
'
23
'
21
'
13
'
24
260 4 ( 300) 3
1
35.
4
36.
37.
Базисное решение, которое даетпоследняя таблица
x1 ( x1 , x 2 , x3 , x 4 , x 5 , x6 ) (0, 75, 300, 0, 225, 0),
f ( x1 ) (C В A0 ) 0 300 0 0 225 300 75 22500.
Это решение не является оптимальным, так
как в f - строке имеется отрицательная
оценка 1 .
Принимая последнюю таблицу за исходную,
повторяем описанный выше процесс
и строим новую симплекс-таблицу (табл. 5.5).
38.
39.
В последней таблице f - строка несодержит отрицательных оценок, что
свидетельствует об оптимальности
полученного решения:
x2 ( x1 , x2 , x3 , x4 , x 5 , x6 )
(42,857; 42,857; 0 ; 4,286; 128,57; 0)
f max f ( x2 ) (CВ A0 )
260 42,857 0 4,286 0 128,57 300 42,857
24000.
40.
Вывод. Предприятие должно выпускать42,857 единиц времени продукцию по
первой технологии и 42,857 единиц
времени по второй. Максимальное
количество изделий при этом – 24000 штук.
Ресурсы сырье и заработная плата будут
использованы полностью. Ресурсы
электроэнергия и накладные расходы
остаются в количествах
x4 4,285; x5 128,57.
41.
Замечания.• Для того, чтобы решить симплексметодом задачу минимизации
необходимо изменить правило выбора
разрешающего столбца (выбирать
столбец
, для которого s 0 ).
Признаком оптимальности допустимого
решения являются условия
s
j 0, j 1, n .
42.
• Если для некоторой симплекс-таблицывсе элементы разрешающего столбца
отрицательны, то целевая функция
неограниченна сверху (при нахождении
максимума) или снизу (при нахождении
минимума) и поставленная задача
решения не имеет.





















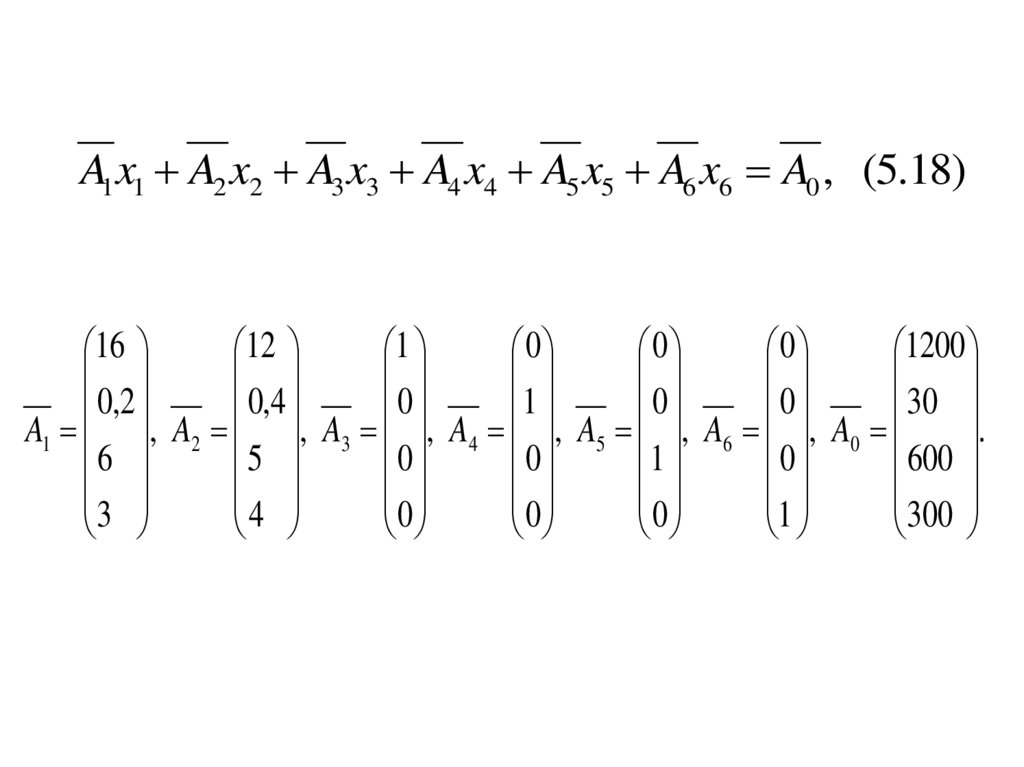


















 Математика
Математика








