Похожие презентации:
Выборочное наблюдение
1. Выборочное наблюдение
Наблюдение бывает:-Сплошное
-Выборочное
Совокупность, из которой производится отбор, называют
генеральной. Совокупность отобранных единиц –
выборочная.
Плюсы выборочного наблюдения:
- Экономия времени и труда.
- Возможность детального исследования каждой единицы
наблюдения при невозможности охвата всей совокупности.
- Большая точность результатов обследования в результате
сокращения ошибок регистрации
Принципы теории выборочного метода:
-Обеспечение случайности попадания единиц.
-Достаточное число единиц.
2.
Основная задача выборочного наблюдения состоит
в том, чтобы на основе характеристик выборочной совокупности
получить достоверные суждения о показателях средней и доли
генеральной совокупности
Классификация выборочного наблюдения:
1. По виду различают:
–
индивидуальный;
–
групповой;
–
комбинированный отбор.
При индивидуальном отборе отбирают отдельные единицы
совокупности.
При групповом отборе отбирают качественно однородные группы или
серии изучаемых единиц.
Комбинированный отбор предполагает сочетание первого и второго
видов.
2.
По методу отбора различают:
–
повторную выборку;
- бесповторную выборку
3.
При повторной выборке общая численность единиц
При бесповторной выборке единица совокупности,
3.
генеральной совокупности в процессе выборки остаётся
неизменной. Повторная выборка встречается редко.
попавшая в выборку, в генеральную совокупность на
возвращается, в дальнейшей выборке не участвует. При
бесповторной выборке генеральная совокупность
сокращается
По способу отбора. Различают:
–
большие выборки
–
малые выборки
Малые выборки обычно меньше 30 единиц. Наибольшее
распространение получили случайная, механическая,
типическая, серийная и комбинированная выборки.
4. Основные характеристики показателей совокупности
Основные характеристики показателей
совокупности
N – объём генеральной совокупности
n – объём выборки
x - генеральная средняя
- выборочная средняя
р – генеральная доля (это доля единиц, обладающих
данным значением признака в общем числе единиц
генеральной совокупности)
w – выборочная доля
2
G - генеральная дисперсия
~x
• S 2- выборочная дисперсия
• G – среднеквадратическое отклонение генеральной
совокупности
• S - среднеквадратическое отклонение выборки
5. Ошибки выборки
Доля выборки [1]n
kв
N
Применяя выборочный метод в статистике обычно
используют вида обобщающих показателей:
-Средняя величина количественного признака
-Относительная величин альтернативного признака
Выборочная доля [2], т. е. отношение числа единиц,
обладающих изучаемым признаком к общему числу единиц
выборочной совокупности.
m
w
n
6.
• Ошибка выборки – это разность соответствующихвыборочных и генеральных характеристик.
Для средне количественного признака [3].
~x ~x x
Для альтернативного признака [4].
w w p
• Ошибка выборки зависит:
От объёма выборки (чем больше численность, тем меньше
ошибка).
От степени варьирования признака. Степень варьирования
характеризуется дисперсией. (Чем меньше дисперсия, тем
меньше ошибка).
7. Нахождение реальной ошибки выборки
1 При случайном повторном отборе средние ошибкирассчитываются:
-Для средне количественного признака [5].
G2
x
n
- для альтернативного признака [6].
p(1 p)
p
n
Поскольку на практике дисперсия признака в генеральной
совокупности неизвестна, то используют выборочную
дисперсию.
x
S2
n
w(1 w)
p
n
Однако дисперсия выборочной совокупности не равна дисперсии
генеральной совокупности. Но в теории вероятности доказано, что
8.
Генеральная дисперсия выражается через выборочную:n
G S *
n 1
2
2
При малой выборке средняя ошибка равна
м .в .
2.
S2
n 1
При случайном бесповторном отборе средние ошибки
выборки имеют вид:
S2
n
~x
(1 )
n
N
-
Для альтернативного признака [12].
w(1 w)
n
w
(1 )
n
N
-
n
(1 )
Т. к. n<N, то
N <1 всегда. Поэтому средняя ошибка при
бесповторном отборе всегда будет меньше, чем при
повторном.
9.
• Механическая выборкаМеханическая выборка состоит в том, что отбор единиц в
выборочную совокупность из генеральной, разбитой по
нейтральному признаку на равные интервалы, производится
таким образом, что из каждой такой группы в выборку
отбирается лишь 1 единица.
• Типическая выборка
Применяется для отбора единиц из неоднородной
совокупности. Используется в тех случаях, когда все единицы
генеральной совокупности можно разбить на несколько
качественно однородных однотипных групп по признакам,
влияющим на изучаемый показатель.
Типическая выборка даёт более точные результаты по
сравнению с другими способами отбор единиц в выборочную
совокупность. При определении средней ошибки типической
выборки в качестве показателя вариации выступает средняя из
групповых дисперсий. Среднюю ошибку выборки находят по
формуле:
Для повторного отбора [15].
~x
Gx
r
2
10.
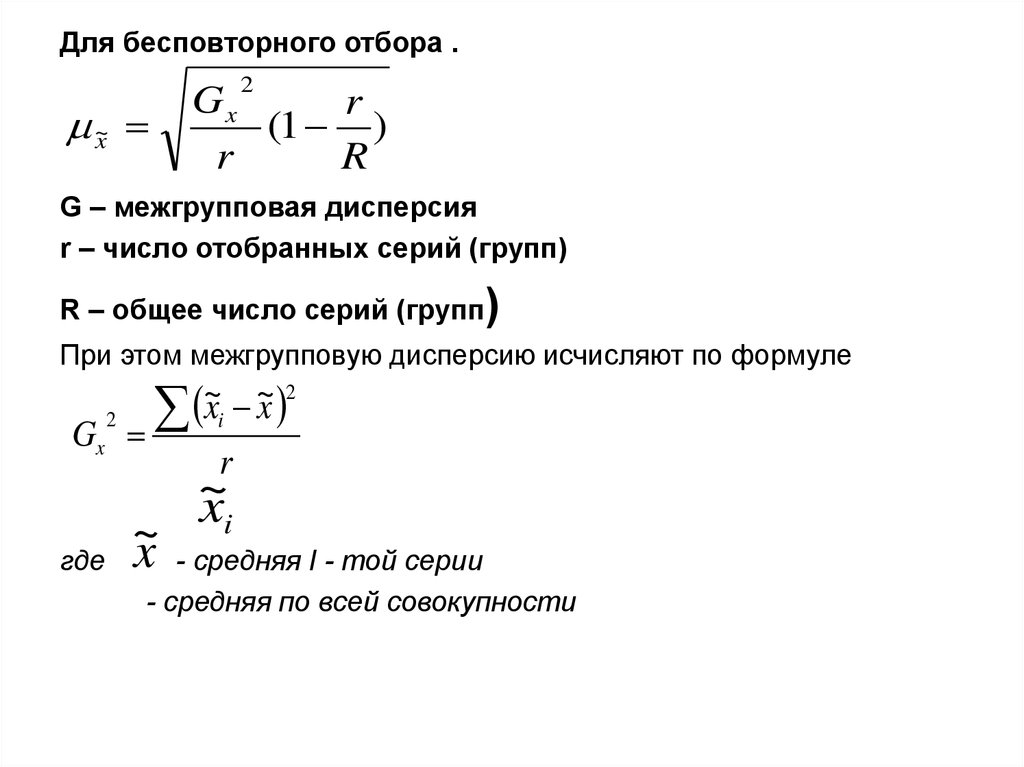
Для бесповторного отбора .2
Gx
r
(1 )
r
R
~x
G – межгрупповая дисперсия
r – число отобранных серий (групп)
R – общее число серий (групп)
При этом межгрупповую дисперсию исчисляют по формуле
Gx
2
где
~x ~x 2
i
r
~
x
~
xi
- средняя I - той серии
- средняя по всей совокупности
11. Распространение выборочных результатов на генеральную совокупность
• В каждой конкретной выборке расхождение между выборочнойсредней и ~
x x генеральной может быть меньше средней
ошибки выборки, больше или равным ей. Каждое из этих
~
расхождений имеет различную вероятность. Поэтому x x
можно рассматривать как предельную ошибку. Предельную
ошибку выборки при повторном отборе рассчитывают по
формуле
2
S
~x t * ~x t
n
t – нормативное отклонение (коэффициент доверия)
~x - средняя ошибка выборки
Предельная ошибка выборки для доли:
-при повторном отборе [19]
w(1 w)
w t *
n
12.
На основании теоремы Чебышева с уточнениями Ляпунова свероятностью сколь угодно близкой к единице можно
утверждать, что при достаточно большом объёме выборки и
ограниченной генеральной дисперсии выборочные
обобщающие показатели будут сколь угодно мало отличаться от
соответствующих генеральных показателей.
p ~
x x ~
x Ф(t )
где
1
Ф(t )
2
t
e
t
x2
2
dx
13.
Предельная ошибка выборки позволяет определитьпредельные значения характеристик генеральной
совокупности и их доверительные интервалы
• Для средней:
x ~
x ~
x
~
x ~
x x ~
x ~
x
• Для доли:
p w w
w w p w w
Это означает, что с заданной вероятностью можно
утверждать, что значение генеральной средней
следует ожидать в пределах от до .
14.
Примеры:1. Для определения скорости расчётов с кредиторами в
коммерческом банке была произведена выборка 100 платёжных
поручений, по которым средний срок перечислений оказался
равным 2 дням со стандартным отклонением 6 дней.
Необходимо с вероятностью 0,954 определить предельную
ошибку выборочной средней и доверительные пределы средней
продолжительности расчётов предприятий.
~x 22
S 6
p 0,954
S2
~
x t
n
Согласно теореме Чебышева t=2, тогда предельная ошибка
выборки равна
36
~
x 2
1,2
100
15.
Предельная относительная ошибка выборки:~
x
% ~ * 100 5,45
x
~
x ~
x x ~
x ~
x
22 1,2 x 22 1,2
20,8 x 23,2
Таким образом, с вероятностью 0,954 можно
утверждать, что средняя продолжительность
расчётов колеблется в пределах от 20,8 до 23,2 дня.
16.
Среди выборочно обследованных 1000 семей
малообеспеченными оказалось 300 семей. Выборка была
механическая 2%-ная. Требуется с вероятностью 0,997
определить долю малообеспеченных семей во всём регионе.
300
w
0,3
1000
n
0,02
N
t 3
Механическая выборка всегда бесповторная.
w t
w(1 w)
n
0,3 * 0,7
(1 ) 3
(1 0,02)
n
N
1000
Предельная ошибка выборки:
w
*100 4,7
w
0,3 0,014 p 0,3 0,014
0,286 w 0,314
%
С вероятностью 0,997 можно утверждать, что доля
малообеспеченных семей колеблется от 28,6% до 31,4%.
17. Определение необходимого объёма выборки
• Формулу для определения необходимой численности выборкиполучают из формул ошибки выборки.
n
n
n
n
t 2S 2
x
2
t 2 w(1 w)
w
2
- для повторного отбора
t 2S 2 N
x N t2N 2
2
t 2 w(1 w) N
w N t w(1 w)
2
2
n - для бесповторного отбора
18.
Пример:Для определения среднего возраста 1200 студентов проводят
выборочное обследование методом случайного бесповторного
отбора. Предварительно установлено, что
среднеквадратическое отклонение возраста студентов равно 10
годам. Сколько студентов нужно обследовать, чтобы с
вероятностью 0,954 средняя ошибка выборки не превышала 3-х
лет.
t 2
t 2S 2N
1200 * 2 2 * 10
n 2
2
43
2
2
2
2
3 * 10 2 * 10
x N t N
Таким образом, выборка численностью 43 человека обеспечивает
заданную точность при бесповторном отборе

















 Математика
Математика








