Выборочное наблюдение

1. Статистика

2. Тема: Выборочное наблюдение

1.
2.
3.
4.
5.
Выборка в системе методов несплошного
статистического наблюдения
Основные этапы выборочного наблюдения
Методы и способы, обеспечивающие
репрезентативность выборки
Основные виды статистических показателей
генеральной совокупности, оцениваемые по
данным выборочного наблюдения
Определение объема выборочной совокупности

3. 1. Выборка в системе методов несплошного статистического наблюдения

Статистическое наблюдение – это научно организованный
учет фактов о явлениях общественной жизни и сбор полученных на
основе такого учета массовых первичных данных. Является первым
этапом любого статистического исследования.
По степени охвата единиц совокупности различают следующие виды
статистических наблюдений:
сплошные - учёт всех единиц изучаемой совокупности
несплошные - учёт части единиц совокупности.

4.

Несплошное наблюдение может быть организовано как:
наблюдение основного массива
выборочное наблюдение
монографическое наблюдение.
Выбор вида и метода статистического наблюдения определяется:
• материальными и трудовыми ресурсами, имеющимися в наличии у
организаторов наблюдения;
• составом решаемых статистических задач;
• объемом статистической совокупности;
• необходимой точностью получаемых результатов.

5.

Из перечня несплошных наблюдений статистика отдает
предпочтение выборочным обследованиям, поскольку существует
теория, описывающая поведение выборок.
Ведущий принцип, лежащий в основе процедуры формирования
выборки, – это принцип случайности или рандомизации (от англ. random
– случайный).
«Выборочное исследование … обогащает рабочий инвентарь
статистика орудием, облегчающим работу в ходе наблюдения, не
поступаясь при этом научной объективностью результата».
«Теоретические основания выборочного метода» (1924)
БОУЛИ (BOWLEY) Артур
1869-1957
Англия

6.

В современной статистической практике при проведении
статистических наблюдений используют сочетание сплошного и
выборочного методов, получившее название комбинированного
метода статистического наблюдения. Он реализуется в двух формах:
чередование во времени (например: в один год – сплошное, в другой
выборочное)
одновременное использование (например: часть совокупности (или
ее свойств) наблюдается на сплошной основе, а другая часть – на
выборочной).

7. «О развитии малого и среднего предпринимательства в Российской Федерации» Федеральный Закон РФ от 24. 07.2007 № 209-ФЗ

1.
2.
3.
Статья 5. Федеральные статистические наблюдения
за деятельностью субъектов малого и среднего предпринимательства
Федеральные статистические наблюдения за деятельностью субъектов
малого предпринимательства в Российской Федерации осуществляются
путем
проведения
сплошных
статистических
наблюдений
за
деятельностью субъектов малого и среднего предпринимательства и
выборочных статистических наблюдений за деятельностью отдельных
субъектов малого и среднего предпринимательства на основе
представительной (репрезентативной) выборки.
Сплошные статистические наблюдения за деятельностью субъектов
малого и среднего предпринимательства проводятся один раз в пять лет.
Выборочные
статистические
наблюдения
проводятся
путем
ежемесячных и (или) ежеквартальных обследований деятельности
малых предприятий (за исключением микропредприятий) и средних
предприятий. Выборочные статистические наблюдения проводятся путем
ежегодных обследований деятельности микропредприятий. Порядок
проведения выборочных статистических наблюдений определяется
Правительством Российской Федерации.

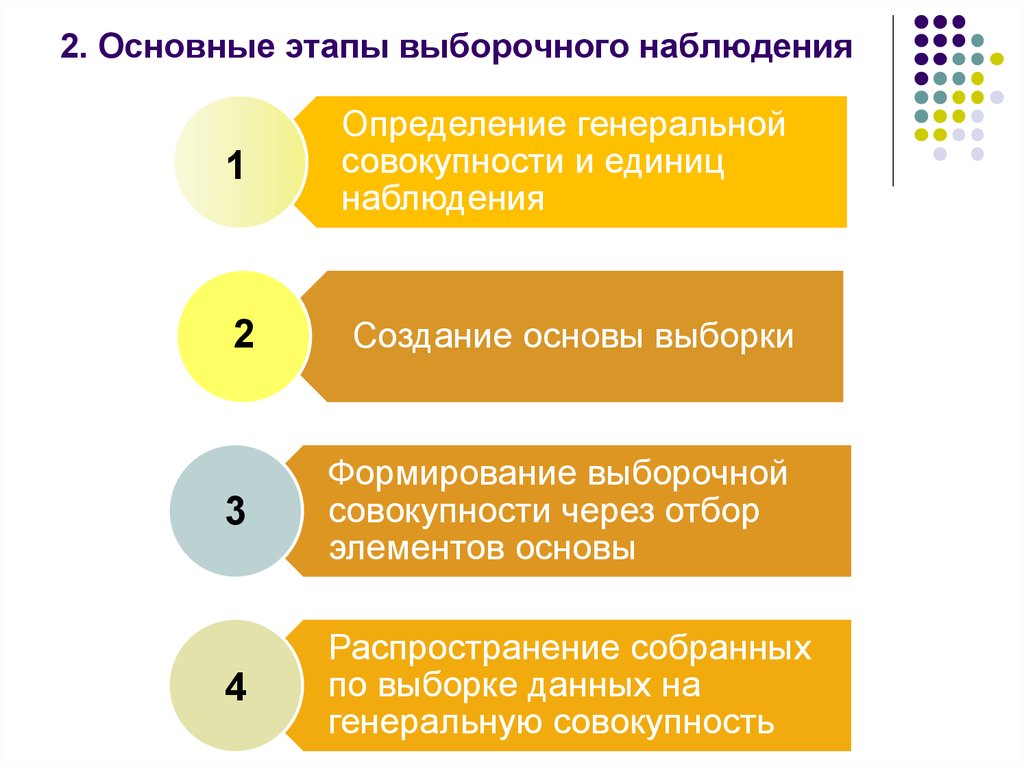
8. 2. Основные этапы выборочного наблюдения

1
Определение генеральной
совокупности и единиц
наблюдения
2
Создание основы выборки
3
Формирование выборочной
совокупности через отбор
элементов основы
4
Распространение собранных
по выборке данных на
генеральную совокупность

9.

Генеральная совокупность - множество реально или гипотетически
существующих объектов или явлений, из которых тем или иным
способом формируется совокупность выборочная (население страны,
домашние хозяйства региона, предприятия отрасли и т.п.).
Теоретически генеральная совокупность может быть как конечной,
так и бесконечной. Однако для органов государственной статистики
практический интерес представляет конечная генеральная
совокупность. Конечная совокупность имеет место, например, при
обследовании семейных бюджетов, когда выборка берется из
совокупности домохозяйств, фактически имеющихся в стране, а затем
осуществляются наблюдения за доходами и расходами в отобранных
домохозяйствах. Конечная совокупность также имеет место при
экономических обследованиях организаций - резидентов рынка страны.

10.

Государственное статистическое наблюдение базируется на
создании и поддержании в актуальном состоянии статистических
основ – перечней (списков) единиц реальных совокупностей с
набором признаков, соответствующих целям статистических
исследований.
Информационными источниками для основы выборки являются:
1. Статистический регистр Федеральной службы государственной
статистики (Статрегистр Росстата).
2. База данных государственной бухгалтерской отчетности организаций
(БД БОО).

11. Примеры

ПРИМЕРЫ

12. Основы выборки при проведении выборочных статистических наблюдений за сельскохозяйственным производством в крестьянских

(фермерских) хозяйствах
Основа выборки для получения информации по растениеводству:
Совокупность 1 – список крестьянских (фермерских) хозяйств региона,
имеющих посевы зерновых и зернобобовых культур, ранжированный по
возрастанию показателя «Посевная площадь зерновых и зернобобовых
культур».
Совокупность 2 – список крестьянских (фермерских) хозяйств региона,
имеющих посевы сахарной свеклы, ранжированный по возрастанию
показателя «Посевная площадь сахарной свеклы».
Основа выборки для получения информации по животноводству:
Совокупность 1 – список крестьянских (фермерских) хозяйств региона,
имеющих поголовье крупного рогатого скота, ранжированный по
возрастанию показателя «Численность крупного рогатого скота».
Совокупность 2 – список крестьянских (фермерских) хозяйств региона,
имеющих поголовье свиней, ранжированный по возрастанию показателя
«Численность свиней».

13. Основа выборки при проведении выборочного статистического наблюдения за перевозочной деятельностью предпринимателей (физических

лиц) – владельцев грузовых автомобилей
Цель – оценка сводных статистических показателей об объемах грузовых
перевозок, осуществляемых предпринимателями в регионе в течение
отчетного периода.
Объектом исследования является совокупность физических лиц владельцев грузовых автомобилей, имеющих лицензии на занятие
коммерческой перевозочной деятельностью по состоянию на 1 января
текущего года, а единицами наблюдения - конкретные предприниматели.
Основа выборки - пофамильный список предпринимателей в алфавитном
порядке. Каждому предпринимателю присваивается номер от 1 до N (N общее число предпринимателей в регионе).
Основа выборки формируется территориальными органами
государственной статистики на базе регистра лицензиатов, составляемого
территориальными отделениями Российской транспортной инспекции (РТИ).
Из регистра отбираются лицензиаты, являющиеся индивидуальными
предпринимателями (физическими лицами) и получившие лицензии на
право осуществления грузовых перевозок на коммерческой основе
независимо от вида сообщения.

14.

Федеральный Закон Российской Федерации от 20.08.2004 г. N 113-ФЗ
«О ПРИСЯЖНЫХ ЗАСЕДАТЕЛЯХ ФЕДЕРАЛЬНЫХ СУДОВ ОБЩЕЙ ЮРИСДИКЦИИ В
РОССИЙСКОЙ ФЕДЕРАЦИИ»
Статья 5. Порядок и сроки составления списков кандидатов в присяжные
заседатели
3. Списки кандидатов в присяжные заседатели составляются исполнительнораспорядительными органами муниципальных образований отдельно по каждому
муниципальному образованию субъекта Российской Федерации на основе
персональных данных об избирателях, входящих в информационные ресурсы
Государственной автоматизированной системы Российской Федерации "Выборы",
путем случайной выборки установленного числа граждан. При этом из числа
отобранных граждан исключаются лица, которые не могут быть присяжными
заседателями в соответствии с частью 2 статьи 3 настоящего Федерального закона
(признанные судом недееспособными или ограниченные судом в дееспособности).

15. 3. Методы и способы, обеспечивающие репрезентативность выборки

Формирование выборки осуществляется различными методами
и способами.
Различают два метода отбора:
повторный
бесповторный.
Используют следующие способы отбора:
• собственно-случайный (простая случайная выборка)
• механический (систематический)
• расслоенный (типический)
• серийный (гнездовой).

16. Собственно-случайный отбор

Собственно-случайным отбором называется способ, при котором извлечение
единиц из совокупности для обследования осуществляется методом
жеребьевки или с использованием таблиц или генератора случайных чисел без
деления этой совокупности на какие-либо классы или группы.
ПРИМЕР (условный): Сформируйте собственно-случайную бесповторную
выборку объемом 3 единицы из следующей совокупности образовательных
учреждений высшего профессионального образования города Новосибирска:
НГАЭиУ, НГТУ, НГУ, СГГА, СибГУТИ, НГАСУ, СГУПС. Используйте следующую
последовательность случайных цифр: 87097253671352349.
Шаг 1: (нумеруем единицы совокупности)
НГУЭиУ – 1; НГТУ – 2; НГУ – 3; СГГА – 4; СибГУТИ – 5; НГАСУ – 6; СГУПС – 7.
Шаг 2: (отбираем случайные цифры)
7; 2; 5.
Шаг 3 (формируем выборку)
СГУПС; НГТУ; СибГУТИ

17. Механический (систематический) отбор

Это способ отбора, при котором выборочная совокупность
формируется на основе отбора единиц через определенный интервал,
определяемый как N/n.
В теории статистики систематический отбор считается более
эффективным, чем простая случайная выборка. Также его легче
осуществлять при работе вручную. Однако это обстоятельство
потеряло свою актуальность в связи с широким распространением
персональных компьютеров.

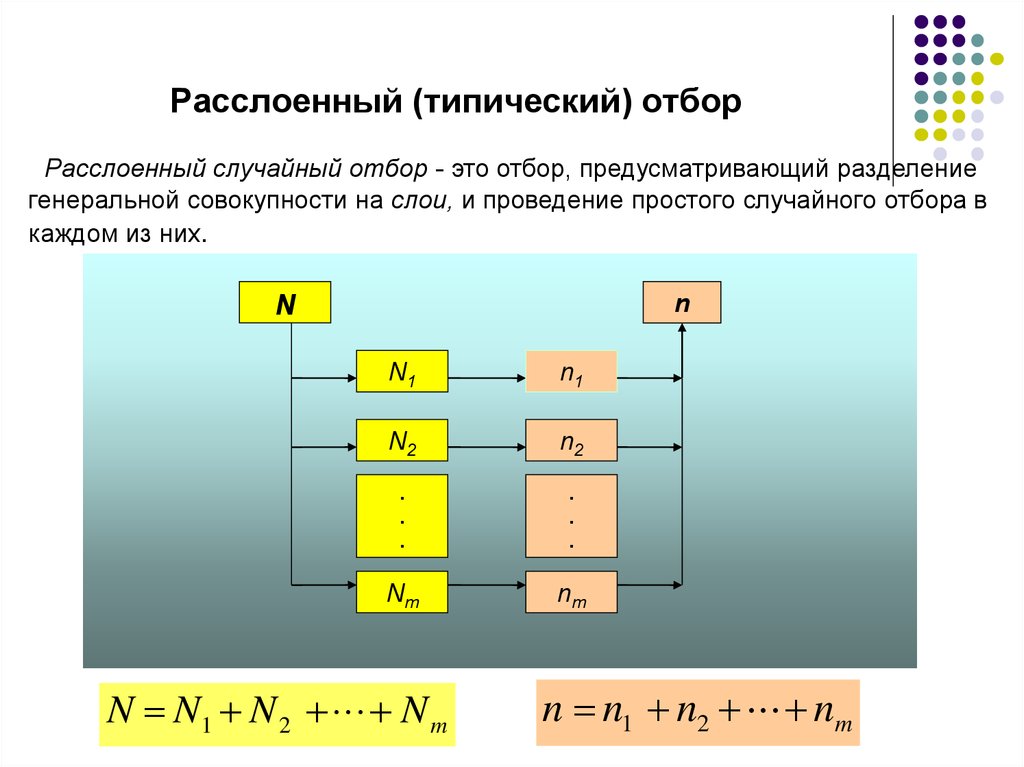
18. Расслоенный (типический) отбор

Расслоенный случайный отбор - это отбор, предусматривающий разделение
генеральной совокупности на слои, и проведение простого случайного отбора в
каждом из них.
n
N
N1
n1
N2
n2
.
.
.
.
.
.
Nm
nm
N N1 N 2 N m
n n1 n2 nm

19.

Число единиц, отбираемых из каждого слоя, определяется одним из
следующих методов:
непропорциональным
пропорциональным
оптимальным
n
ni
m
Ni
ni n
N
N i i
ni n
Ni i
ni n
N i Wi 1 Wi
N
i
Wi 1 Wi

20. Пример

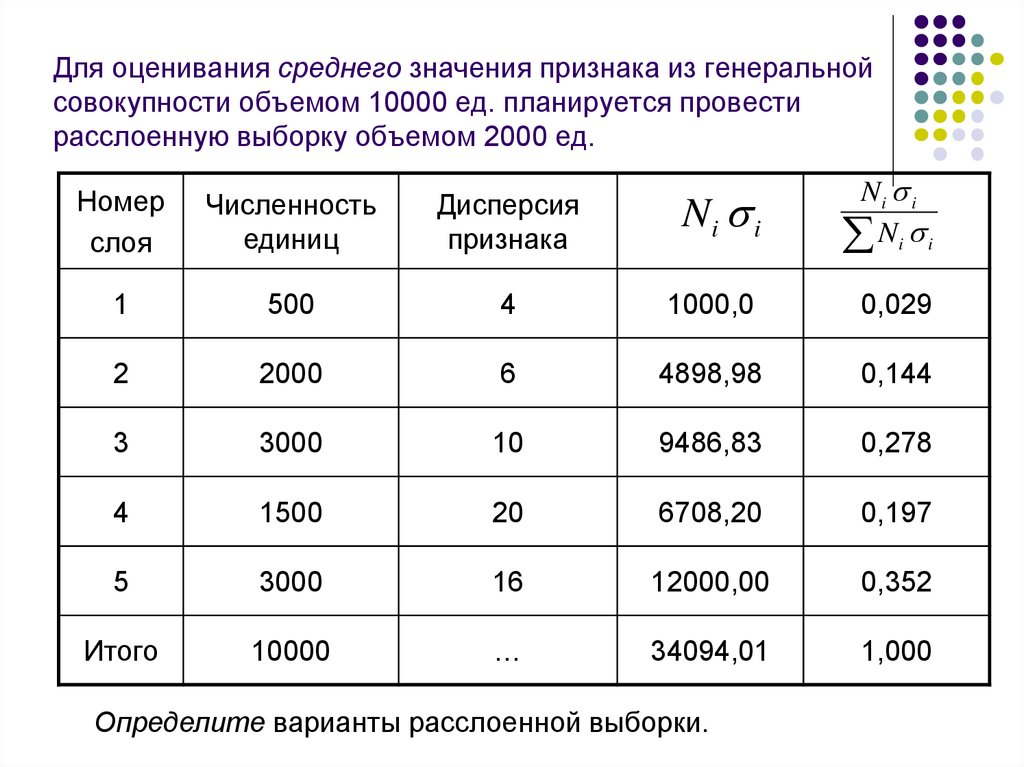
ПРИМЕР

21. Для оценивания среднего значения признака из генеральной совокупности объемом 10000 ед. планируется провести расслоенную

выборку объемом 2000 ед.
Ni i
Ni i
Ni i
4
1000,0
0,029
2000
6
4898,98
0,144
3
3000
10
9486,83
0,278
4
1500
20
6708,20
0,197
5
3000
16
12000,00
0,352
Итого
10000
…
34094,01
1,000
Номер
слоя
Численность
единиц
Дисперсия
признака
1
500
2
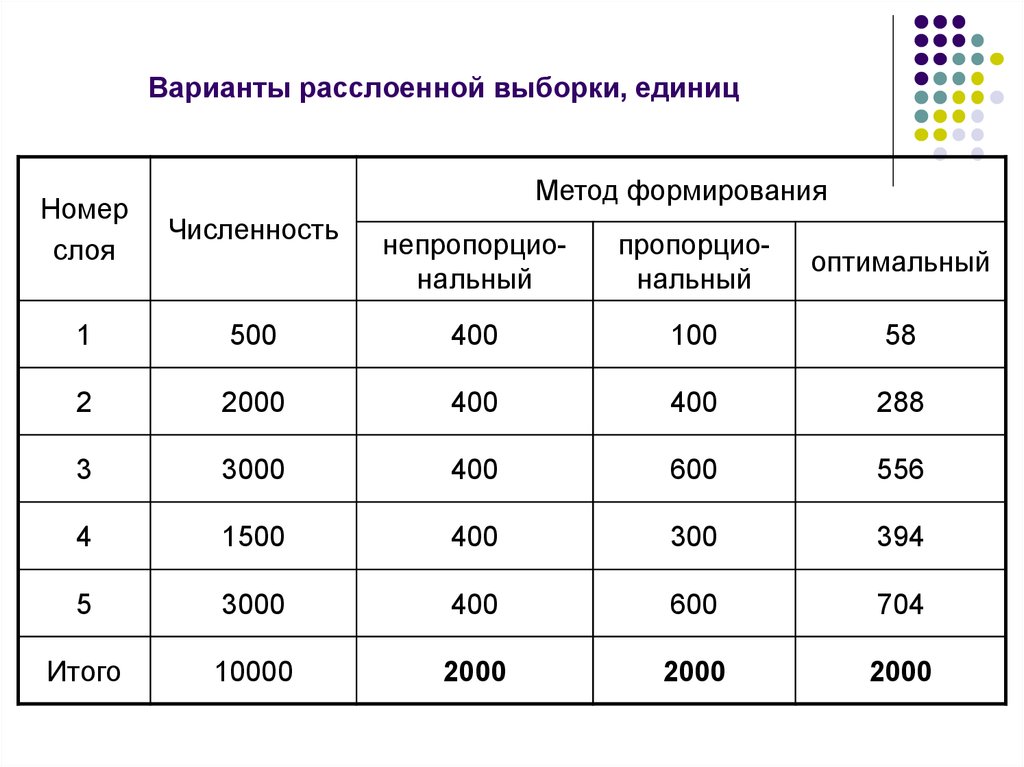
Определите варианты расслоенной выборки.

22. Варианты расслоенной выборки, единиц

Метод формирования
Номер
слоя
Численность
1
непропорциональный
пропорциональный
оптимальный
500
400
100
58
2
2000
400
400
288
3
3000
400
600
556
4
1500
400
300
394
5
3000
400
600
704
Итого
10000
2000
2000
2000

23. Серийный (гнездовой) отбор

Серийный (гнездовой) отбор – способ формирования выборки, при котором
единица отбора состоит из группы или гнезда более мелких единиц, называемых
элементами.
Гнездовая выборочная единица – группа элементов, которая в процессе
извлечения выборки рассматривается как одна единица.
Применение гнездового отбора в статистической практике обусловлено
двумя основными причинами:
1. Для обследования может не существовать основы выборки (списка
элементов совокупности), а ее составление или невозможно, или
обошлось бы дорого.
2. Экономические соображения могут диктовать выбор более крупных
единиц отбора.

24. 4. Основные виды статистических показателей генеральной совокупности, оцениваемые по данным выборочного наблюдения

В практике выборочного наблюдения статистический показатель
имеет более узкий смысл, чем в статистике вообще.
Как правило, определяют и оценивают четыре их вида:
суммарное значение признака в совокупности
среднее значение признака в совокупности
доля единиц наблюдения, обладающих изучаемым
значением признака
число единиц наблюдения, обладающих изучаемым
значением признака
Каждый из этих показателей может быть выражен алгебраически.

25. Основные виды статистических показателей генеральной совокупности и их оценка

Совокупность
Оцениваемый показатель
генеральная
выборочная
n
N
Суммарное значение признака
X x
i 1
Среднее значение признака
Доля единиц наблюдения,
обладающих изучаемым
значением признака
Число единиц наблюдения,
обладающих изучаемым
значением признака
1
X
N
x x
i
i 1
N
x
i 1
A
P
N
A N P
i
i
n
1
x~ xi
n i 1
a
W
n
a n W

26. Основные виды статистических показателей генеральной совокупности и их оценка

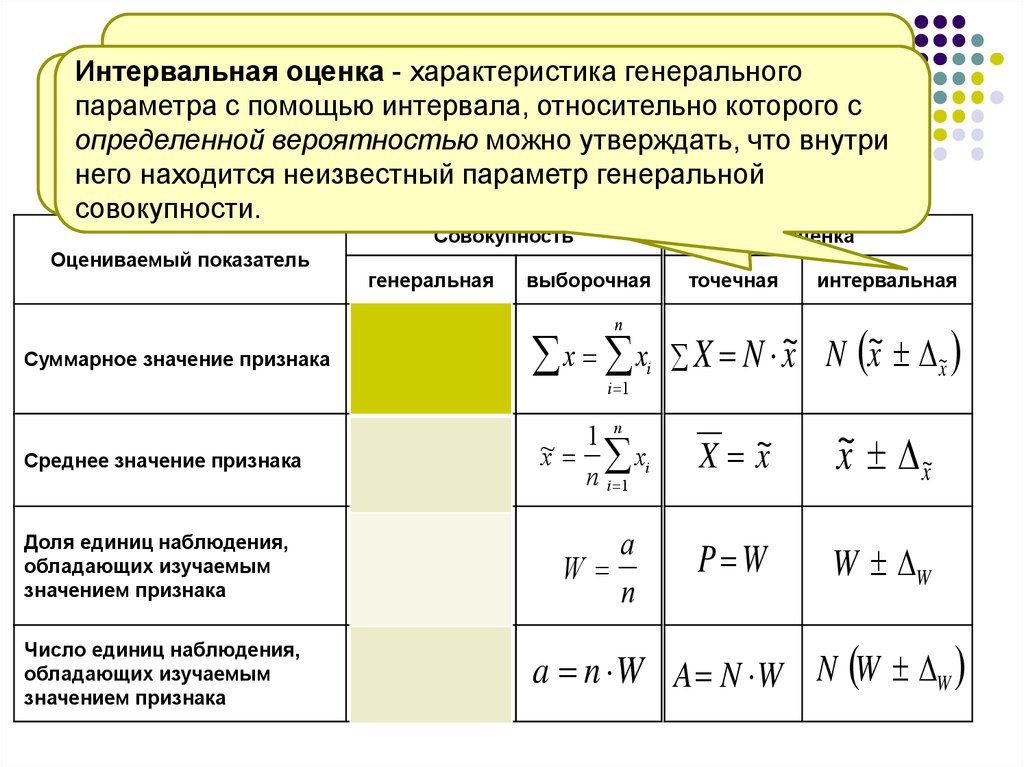
Оценкой называют
характеристику
Интервальная
оценка приближенную
- характеристика
генерального
неизвестного
генеральной
совокупности,
Основные
виды
статистических
показателей
Точечная
оценка
-параметра
приближенная
характеристика
параметра
с помощью
интервала,
относительно
которого с
полученную
по данным
выборочного
генеральной
совокупности
инаблюдения.
их оценка
неизвестного
параметра
генеральной
определенной
вероятностью
можносовокупности
утверждать,
что внутри
с него
помощью
одного
числа.
находится
неизвестный
параметр генеральной
совокупности.
Совокупность
Оцениваемый показатель
генеральная
выборочная
X x
i 1
Среднее значение признака
Доля единиц наблюдения,
обладающих изучаемым
значением признака
Число единиц наблюдения,
обладающих изучаемым
значением признака
1
X
N
~
x
x
X
N
x
i
i
i 1
N
x
i 1
A
P
N
A N P
точечная
n
N
Суммарное значение признака
Оценка
i
n
1
x~ xi
n i 1
a
W
n
интервальная
N ~x ~x
X ~x
~x ~
x
P W
W W
a n W A N W N W W

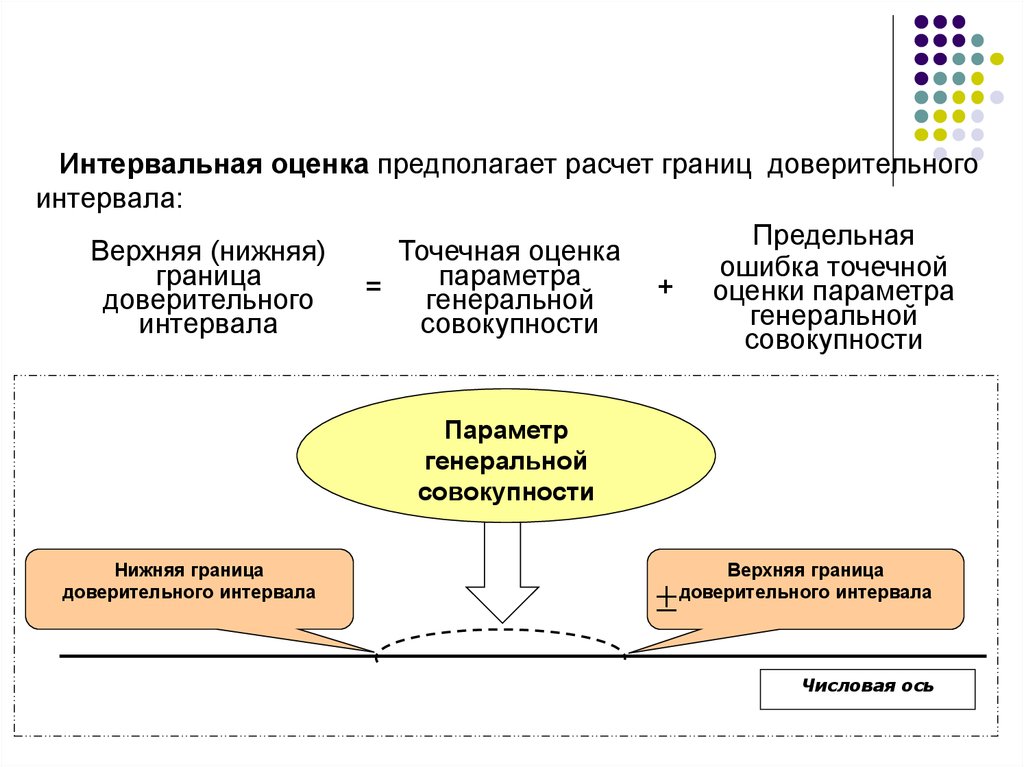
27.

Интервальная оценка предполагает расчет границ доверительного
интервала:
Предельная
Верхняя (нижняя)
Точечная оценка
ошибка точечной
граница
параметра
=
+ оценки параметра
доверительного
генеральной
генеральной
интервала
совокупности
совокупности
Параметр
генеральной
совокупности
Нижняя граница
доверительного интервала
Верхняя граница
доверительного интервала
Числовая ось

28.

Ошибка выборки – расхождение между значением характеристики,
полученной в ходе конкретного исхода выборочного наблюдения, и
параметром генеральной совокупности.
Различают ошибки:
среднюю;
предельную (максимальную).
∆
Величина предельной (максимальной) ошибки зависит от размера
средней ошибки.

29. Формулы расчета предельных ошибок выборки

Оцениваемый показатель
Суммарное значение признака
Среднее значение признака
Доля единиц наблюдения,
обладающих изучаемым
значением признака
Число единиц наблюдения,
обладающих изучаемым
значением признака
Размер предельной ошибки
абсолютный
относительный
N t ~x N ~x
N t ~x
~x
100
100
~
~
Nx
x
~x t ~x
~x
~x 100
W
100
W
W t W
N t W N W
N t W
100 W 100
NW
W

30. Формулы расчета средних ошибок выборки

Метод отбора
Способ
отбора
повторный
для
выборочной
средней
бесповторный
для
выборочной
доли
для
выборочной
средней
для
выборочной
доли
W (1 W )
n
2
n
(1 )
n
N
W (1 W )
n
(1 )
n
N
2
n
W (1 W )
n
2
n
(1 )
n
N
W (1 W )
n
(1 )
n
N
x2
r
r
Собственнослучайный
(механический)
Расслоенный
(пропорциональный)
Серийный
2
n
2
W
x2
r
(1 )
r
R
W2
r
(1 )
r
R

31.

Теоретической основой расчета предельной ошибки выборочной
средней является известная центральная предельная теорема, общие
достаточные условия которой были обоснованы П.Л.Чебышевым и
А.М. Ляпуновым:
P ~
x X t F(t)
F(t)
1
2
t
e
t2
2
dt
t
Значения этой функции при различных величинах t табулированы.
Наиболее часто используемые уровни вероятностей и соответствующие
им значения t:
t
P
Чебышев
Пафнутий Львович
(1821-1894)
1,00
0,683
1,96
0,950
2,00
0,954
3,00
0,997
Ляпунов
Александр Михайлович
(1857-1918)

32. Способ расчета границ и форма записи доверительного интервала (при оценивании генеральной средней)

~
X x ~x
~
x ~x X ~
x ~x
P~
x ~x X ~
x ~x
X ~
x ~ %
x
F(t)

33. Примеры

ПРИМЕРЫ

34.

ПОКАЗАТЕЛИ ТОЧНОСТИ СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ
стоимости основных продуктов питания, потребленных в домашних хозяйствах
России в 2008 году
Значение
показателя,
в среднем на
потребителя,
в месяц, руб.
Коэффициент
вариации
оценки, %
Стандартное
отклонение,
руб.
Интервальная
оценка (Р=0,95)
Хлеб и хлебные продукты
415,8
1,2
5,0
406,0 - 425,6
Картофель
87,7
2,0
1,8
84,2 - 91,2
Овощи и бахчевые
294,2
1,6
4,7
285,0 - 303,4
Фрукты и ягоды
259,2
2,1
5,4
248,6 - 269,8
Мясо и мясные продукты
816,9
2,3
18,8
780,1 - 853,7
Молоко и молочные продукты
396,7
1,8
7,1
382,8 - 410,6
Яйца
58,2
1,4
0,8
56,6 - 59,8
Рыба и рыбные продукты
167,9
2,3
3,9
160,3 - 175,5
158,6
1,7
2,7
153,3 - 163,9
59,2
1,3
0,8
57,6 - 60,8
Сахар и кондитерские
изделия
Масло растительное и другие
жиры
ИСТОЧНИК: Потребление продуктов питания в домашних хозяйствах в 2008 году (по итогам выборочного
обследования бюджетов домашних хозяйств):Стат. бюллетень / Росстат, 2009.

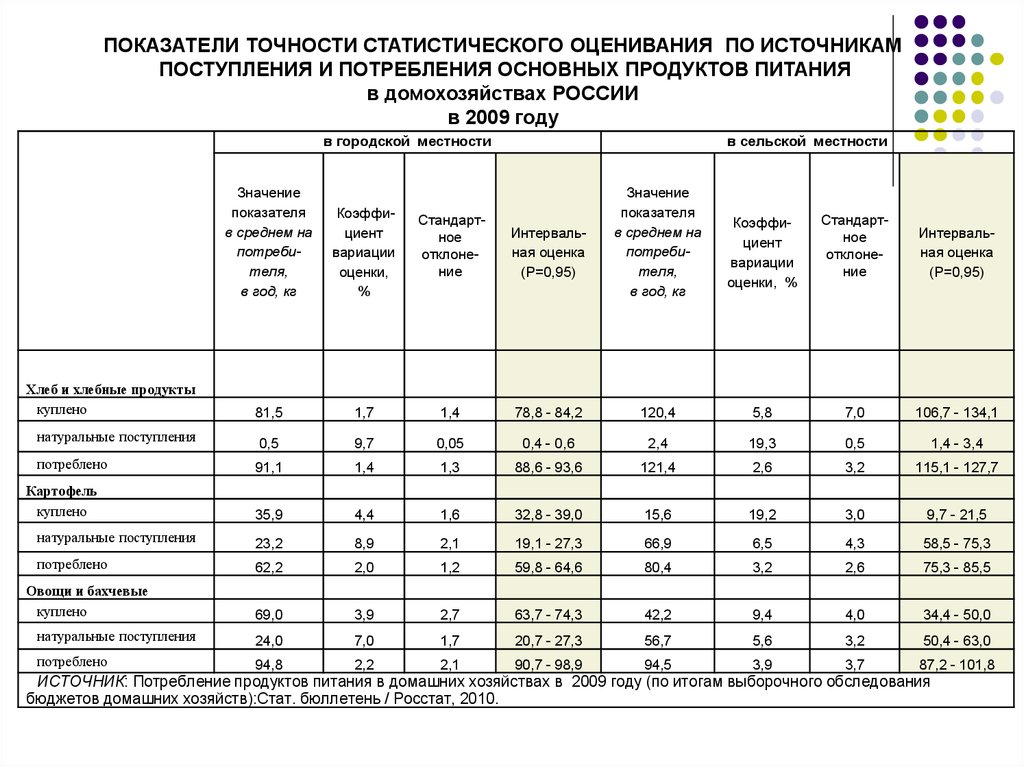
35.

ПОКАЗАТЕЛИ ТОЧНОСТИ СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ ПО ИСТОЧНИКАМ
ПОСТУПЛЕНИЯ И ПОТРЕБЛЕНИЯ ОСНОВНЫХ ПРОДУКТОВ ПИТАНИЯ
в домохозяйствах РОССИИ
в 2009 году
в городской местности
в сельской местности
Значение
показателя
в среднем на
потребителя,
в год, кг
Коэффициент
вариации
оценки,
%
Стандартное
отклонение
Интервальная оценка
(Р=0,95)
Хлеб и хлебные продукты
куплено
81,5
1,7
1,4
78,8 - 84,2
натуральные поступления
0,5
9,7
0,05
потреблено
91,1
1,4
35,9
натуральные поступления
потреблено
Значение
показателя
в среднем на
потребителя,
в год, кг
Коэффициент
вариации
оценки, %
Стандартное
отклонение
Интервальная оценка
(Р=0,95)
120,4
5,8
7,0
106,7 - 134,1
0,4 - 0,6
2,4
19,3
0,5
1,4 - 3,4
1,3
88,6 - 93,6
121,4
2,6
3,2
115,1 - 127,7
4,4
1,6
32,8 - 39,0
15,6
19,2
3,0
9,7 - 21,5
23,2
8,9
2,1
19,1 - 27,3
66,9
6,5
4,3
58,5 - 75,3
62,2
2,0
1,2
59,8 - 64,6
80,4
3,2
2,6
75,3 - 85,5
69,0
3,9
2,7
63,7 - 74,3
42,2
9,4
4,0
34,4 - 50,0
натуральные поступления
24,0
7,0
1,7
20,7 - 27,3
56,7
5,6
3,2
50,4 - 63,0
потреблено
94,8
2,2
2,1
90,7 - 98,9
94,5
3,9
3,7
87,2 - 101,8
Картофель
куплено
Овощи и бахчевые
куплено
ИСТОЧНИК: Потребление продуктов питания в домашних хозяйствах в 2009 году (по итогам выборочного обследования
бюджетов домашних хозяйств):Стат. бюллетень / Росстат, 2010.

36. Задача

Владелец автостоянки опасается обмана со стороны своих
служащих (охраны). В течение года (365 дней) им проведено 40
проверок. По данным проверок среднее число автомобилей,
оставляемых на ночь на охрану, составило 400 единиц, а среднее
квадратическое отклонение их числа – 10 автомобилей.
Считая отбор собственно-случайным, с вероятностью 0,954
определите границы доверительного интервала, в котором следовало
бы ожидать истинное среднее число автомобилей, оставляемых на
ночь на охрану.
Обоснованы ли опасения владельца автостоянки, если по
отчетности охранников за отчетный год среднее число автомобилей,
оставляемых на ночь на охрану, составило 390 автомобилей?

37.

~x t ~x 2
10
40
1
3 avto
365
40
Границы доверительного интервала для среднего значения:
P 397 X 403 0,954
P 400 3 X 400 3 0,954
Можно утверждать, что служащие автостоянки скрывали от учета
в течение года ежедневно не менее 7 автомобилей, оставляемых ее
клиентами на ночь на охрану.
Границы доверительного интервала для суммарного значения признака:
N t ~x 365 3 1095 avto
P 365 400 1095 X 365 400 1095 0,954
P 144905 X 147095 0,954
SU 365 390 144905 142350 144905 2555 avto

38. Задача

Для определения доли и числа домохозяйств, предоставляющих услуги по
временному проживанию лиц, прибывающих в курортную зону региона на
отдых и лечение, была проведена 1%-ная простая случайная выборка.
В результате обследования выявлено, что из 2700 домохозяйств региона,
попавших в выборку, 26,8 % из них являлись квартиросдатчиками.
С вероятностью 0,954 определите доверительные интервалы, в которых
можно ожидать долю и число домохозяйств, предоставляющих услуги по
временному размещению лиц, прибывающих в регион на отдых и лечение.
Оцените, какой удельный вес в общей численности домохозяйств
региона, сдающих жилье туристам и отдыхающим, составляют домохозяйства,
легально работающие в этом сегменте рынка, если известно, что число
официально зарегистрированных индивидуальных предпринимателей,
предоставляющих такие услуги, составляет 8500.

39.

Дано: n 2700
W 0,268
n
0,01
N
Aналоговые органы = 8500
0,268 (1 0,268) (1 0,01)
W t W 2
0,017
2700
P(0, 268 0,017 p 0, 268 0,017) 0,954
P(0, 251 p 0, 285) 0,954
P(0, 251 270000 A 0, 285 270000) 0,954
P(67700 A 73440) 0,954
Максимальная доля
индивидуальных
предпринимателей,
легально работающих
в этом сегменте рынка
8500
100 12,6%
67700

40. 5. Определение объема выборочной совокупности

Определение объема выборки является неотъемлемым этапом при
проектировании выборочного наблюдения.
Теоретическую возможность определения такого объема дает
формула предельной ошибки выборки, адаптированная к различным
методам и способам отбора, а также оцениваемым статистическим
показателям.
Простейшим примером вывода формулы расчета объема выборки
при простом случайном повторном отборе для оценивания среднего
значения выступает уравнение вида:
~x t
2
n
t2 2
n 2
~x

41. Формулы расчета объема выборочной совокупности при различных способах и видах отбора

Вид отбора
Способ
отбора
повторный
Для
выборочной
средней
Собственнослучайный
t
2x
Расслоенный
(пропорциональный)
t
2x
Серийный
2
2
2
2
t 2 ~x2
2~x
бесповторный
Для
выборочно
й доли
Для выборочной
средней
Для выборочной
доли
t 2 w(1 w)
2w
t 2 2 N
N 2x t 2 2
t 2 w(1 w) N
N 2w t 2 w(1 w)
t 2 w(1 w)
2w
t N
t 2 w2
2w
2
2
N t
2
x
2
2
t 2 x 2 R
R t
2
x
2
t 2 w(1 w)N
N 2w t 2 w(1 w)
t 2 w2 R
2
R t w
2
w
2
2

42.

Для определения объема выборки необходимо располагать
информацией двух видов:
требуемой точностью оценивания статистического показателя;
предварительными сведениями об исследуемой совокупности.
Представление о величине вариации признака получают:
• из проведенных ранее или пробных обследованиях;
• по правилу «трех сигм», в соответствии с которым R 6 * ,
R
откуда
;
6
• если известно, хотя бы приблизительно значение средней
величины признака , то V 0,33 0,33 X .
X
• при отсутствии приблизительных данных о величине дисперсии
альтернативного признака, исходя из его максимального значения,
равного 0,25.

43. Тесты для текущего контроля знаний

Отклонение выборочных характеристик от соответствующих
характеристик генеральной совокупности, возникающее вследствие
нарушения принципа случайности отбора, называется: а) случайной
ошибкой регистрации; б) систематической ошибкой репрезентативности;
в) ошибкой исчисления; г) случайной ошибкой репрезентативности.
При определении объема выборки организаторы наблюдения должны
располагать: а) информацией о составе персонала, привлекаемого к
проведению обследования; б) характеристиками требуемой точности
оценивания статистического показателя; в) информацией о сумме средств,
выделяемых на проведение обследования; г) предварительными сведениями
об исследуемой совокупности.
При прочих равных условиях минимальную ошибку обеспечивает
способ отбора: а) собственно-случайный; б) механический; в) расслоенный;
г) серийный.

44.

Как изменится средняя ошибка собственно-случайной повторной
выборки, если объем выборочной совокупности уменьшить в 2
раза: а) возрастет в 2 раза; б) уменьшится в 2 раза; в) возрастет в
1,41 раза; г) возрастет на 29,3%; д) предсказать нельзя.
По данным выборочного обследования 700 контейнеров из 10000,
хранящихся на складе, обнаружено, что 2,6% контейнеров не готовы к
отгрузке. Были бы Вы удивлены, узнав, что в действительности
3,0% из всех контейнеров, хранящихся на складе, не готовы к
отгрузке?
а) да; б) нет; в) предугадать нельзя.
Имеется выборка из 200 пенсионеров поселка. Среднее значение
возраста этой выборки пенсионеров составляет 68,8 лет, а
стандартное отклонение – 10,2 года. Ваш друг утверждает, что
выборочное среднее отличается от среднего возраста всех
пенсионеров поселка на 10,2 года. Прав ли он?
а) безусловно прав; б) абсолютно неправ; в) прав при выполнении
определенных условий надежности оценивания данного показателя;
г) предсказать нельзя.