Похожие презентации:
Компьютерное моделирование динамических процессов в гетерогенных сплошных средах
1. Компьютерное моделирование динамических процессов в гетерогенных сплошных средах.
Член-корреспондент РАНПетров И.Б.
2. Предметные области.
МедицинаСейсмология
Сейсмостойкость
Оборонные и Антитеррористические
задачи
3. Определяющая система уравнений
t v σт
t σ v I v v
т
плотность материала, v скорость, σ симметричный тензор
напряжений Коши, , параметры Ляме,
определяющие свойства упругого материала.
гиперболическая. Собственные значения:
2
2
ci
,
,
,
,
,
,0,0,0
u ( x , y , z , xx , yy , zz , xy , xz , yz )
Используемые реологии: линейно-упругая, вязкоупругая,
упругопластическая, вязко-упругопластическая, повреждаемая.
4. Определяющая система уравнений
) H 2 (σ11 - σ 33 ) σ12 2 H 1υ2
1 (σ - σ
1 H 3
f1 F1 11 22
ρ H 1H 2
x1
H 1H 3
H 2 H1 x2
H 3 x2 H 1H 2
u
u
u
A1
A2
f.
t
x1
x2
A1
1
H1
H
1 υ H 2
υ1
2 x
x
2
1
,
2 H
- σ 33 ) H 3 (σ
H 3
-σ ) σ
υ1
H 2
H1
1 (σ
2 1
f 2 F2 22
22 11 12
υ1
υ2
,
ρ H2 H3
x2
H 2 H1
H 1 H 2 x1
H 3 x1 H 2 H 1
x1
x2
qij11υ2 H
(q
qij21 ) H
2 ij12
1 υ H 2
υ1
2 x
x
H1H 2 x2
2H1H 2
2
1
υ H 3 υ H 3 δij γQ
2
,
1
H x
H 2 x2
ρc
1
1
H
σ
H 3
σ 22
υ2 H 3
1 σ11υ2 H1
1 υ H 2 σ 22υ1 H 2 33 υ1
,
fT
υ1
Q
2 x H H x
H x
ρc H 1H 2 x2
H 1H 2
x2
H
H
x
1
1 2
1
3 1
1
2
2
fij
q
qij22υ2 H
2 ij33
H H
H3
1 2 x1
υ1
0
1 / ρ
0
0
0
0
υ2
0
0
1 / ρ
0
0
0
0
q1111
υ1
(q1112 q1121 ) / 2
0
υ1
1 / ρ
0
0
0
0
0
0
0
0
(q1112 q1121 ) / 2
υ2
q1122
0
υ2
0
0
1 / ρ
0
0
0
0
0
q1211
q2211
q3311
(q1212 q1221 ) / 2
(q2211 q2221 ) / 2
(q3312 q3321 ) / 2
0
0
0
υ1
0
0
0
υ1
0
0
0
υ1
0
0
0
0
0
0
υ2
0
0
0
υ2
0
0
0
υ2
0
0
0
σ11/ ρc
σ11/ ρc
0
0
0
0
υ1
0
0
0
0
υv2
A2
1
(q1212 q1221 ) / 2
q1222
H2
(q2212 q2221 ) / 2
q2222
q3311
(q3312 q3321 ) / 2
qijkl λδij δkl μ(δik δ jl δ jk δil )
σ12 / ρc
IμSij Skl
k
2
σ 22 / ρc
,
5. Определяющая система уравнений
t t, x1 (t, η1 , η2 ) η1 c1 (t, η1 , η2 )dt0
t
x 2 (t, η1 , η2 ) η1 c1 (t, η1 , η2 )dt , x 3 3
1
B
(c1 x1 1 c1 x2 2 )
(c1 x2 1 c2 x1 1 )
tt
t x1
x1 2 1t
1x
2t
2 x
0
x2 2
0
x2 1
x 1
1
1 DetB -1 1x1 2x1 1x2 2x1 1 / ,
Ak ki E kx1 A1 kx2 A2 ,
ut A1u 1 A2u 2 f ,
a ij1 1~t
a ij2 1~t
1 x1 v 1
H1
2 x1 v 1
H1
a 1x1 a 1x2 a
1
ij
1
ij
2
ij
1 x2 v 2
H2
2 x2 v 2
H2
k 1,2,
v
v
1 c 1 x 2 1 2 c 2 x 1 2 1 v~1 ,
H 1
H2
v
v
2 c 2 x 1 1 1 c 1 x 2 1 1 v~2 ,
H 2
H1
x2 1 aij1 x1 1 aij2
a 2 x1 a 2 x2 a
2
ij
1
ij
2
ij
x1 1 aij2 x2 1 aij1
t x2
.
1
1x ,
1
2 x
2
6. Сеточно-характеристический метод
Расщепление по координатамШаг 1
Шаг 2
2D
Гиперболические уравнения ( t)
u n+1 = u n τ(A1 Δ1 + A2 Δ2 A3 Δ3 )u n
u n+1 = u n τ(A1 Δ1 + A2 Δ2 )u n
- трехмерный случай
7.
Граничные и контактные условияКонтактные границы
Внешняя граница
Внешняя сила
Tp f
Условие слипания
va vb V , a b
Скорость на поверхности Условие скольжения
v V
va p vb p, pa pb , a b 0
8. Расчетная сетка
Тетраэдральная сеткаСетки с меняющейся триангуляцией
9. Расчетная сетка
Тетраэдральная сетка10. Тестовые расчёты (одномерная задача)
11. Метод частиц: построение метода
Модель средыd
u
0
dt
x
du 1
0
dt x
de 1
dt
Идеология сглаженных частиц
a x a x x x dx
R
a x a x x x, h dx
R
dS
1
2 S R S R S S S
dt
3
n
K
P P ( ) 1
n 0
1 * 0
ij
2K 2
ij
S S
ij ij
2
S kl S kl
S S 2K
S
K 2
a x
i
a x
x
mi ai
i
xi x, h
mi ai xi x, h
i
x
i
11
12. Метод частиц: монотонизация
Оригинальный методМонотонный метод
d i
ik
mk uk ui
dt
xi
k
d i
ik
*
2 mk uik
ui
dt
xi
k
dui
mk i 2 k 2 ik
dt
k xi
k
i
i * ik
dui
mk
dt
k
i k xi
dei
mk ui uk i 2 k 2 ik
dt
k xi
k
i
*
dei
mk uik * uk ik ik
dt
k
i k xi
dSi
1
2 i i Si Ri Si Ri
dt
3
dSi
1
2 i i Si Ri Si Ri
dt
3
i
Ri
1 mk
ik
ik
u
u
u
u
k
i
k
i
2 k k
xi
xi
i
1 mk
ik
ik
u
u
u
u
k
i
k
i
2 k k
xi
xi
Ri
k
k
mk * ik
ik
uik * ui
uik ui
k
xi
xi
mk * ik
ik
uik * ui
uik ui
k
xi
xi
12
13.
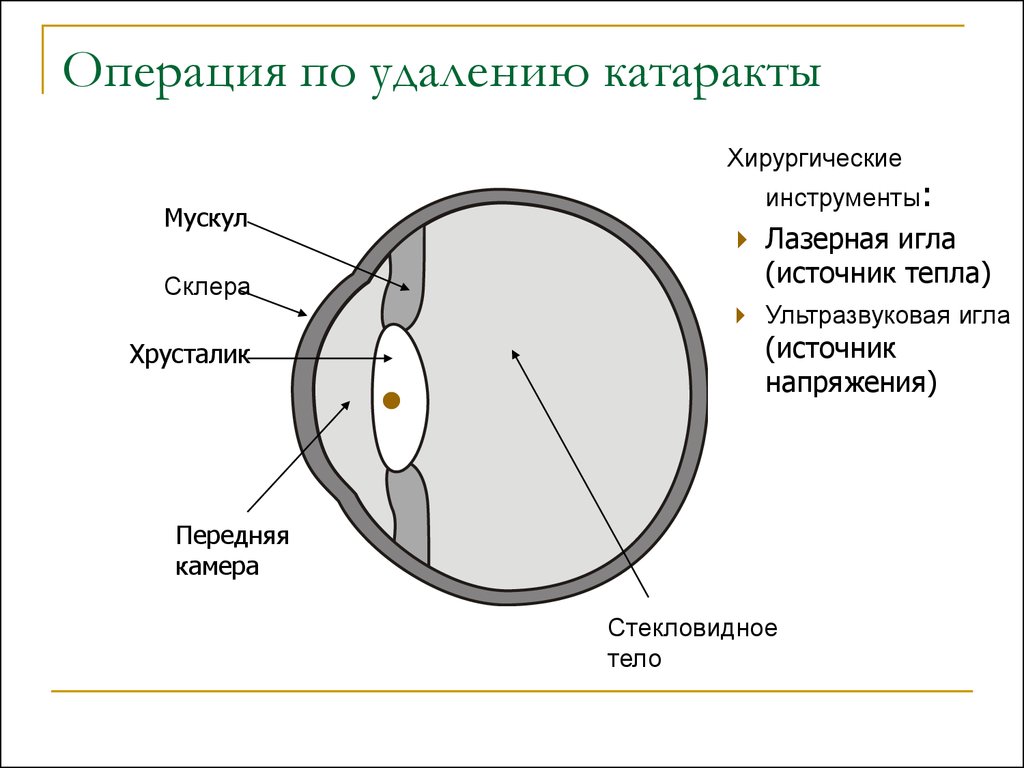
Численное моделирование в медицине.Удаление катаракты.
Модель поражения черепа.
14. Черепно-мозговая травма.
Саггитальное сечение10 м/с импульс
Череп (упругий)
Мозг (вязкоупругий)
10 м/с импульс
Поперечное сечение
15. Модель с мембраной
Свойства материалов:Кость и мембрана:
модуль Юнга E = 1.62·1010 Н/м2
коэффициент Пуассона n = 0.16
Мозг:
модуль Юнга E = 3.5·104 Н/м2
V0 = 1м/с
коэффициент Пуассона n = 0.45
Желудочки:
модуль Юнга E ~ 0
коэффициент Пуассона n ~ 0.5
Реология:
Однородный изотропный линейно-упругий
материал
Контактные условия на границе череп-мозг:
Свободное скольжение
16. Модель поражения черепа
+104 (Сжатие)0
-104 (Растяжение)
17. Сравнение с клиническими данными
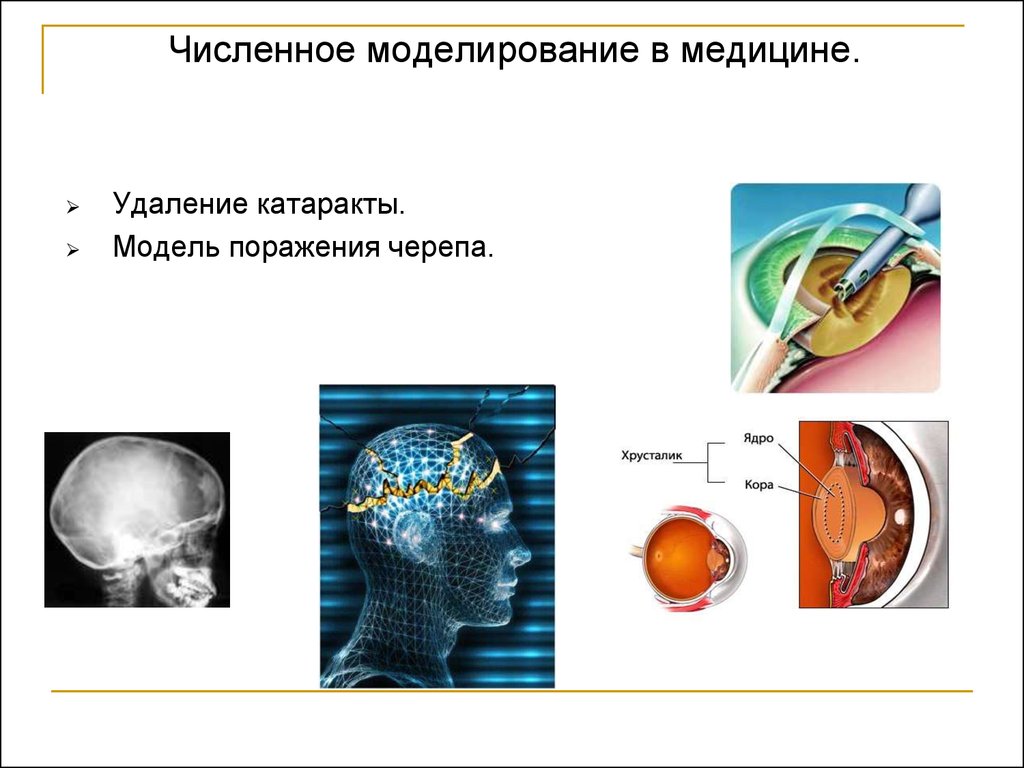
18. Операция по удалению катаракты
ХирургическиеМускул
Склера
инструменты:
Лазерная игла
(источник тепла)
Ультразвуковая игла
Хрусталик
(источник
напряжения)
Передняя
камера
Стекловидное
тело
19.
Лазерная и ультразвуковая операции20.
21.
22.
Задача литотрипсии23.
Моделирование работы сердечноймышцы.
Нормальная скорость,
как функция времени
Мускул
Кровь
24. Моделирование работы сердечной мышцы.
25.
Численное моделирование в геологии26. Численное моделирование в геологии
Трещины и пустоты.27. Трещины и пустоты.
Взрыв рядом с поверхностью.продольные волны
поперечные волны
Волна Релея
28. Взрыв рядом с поверхностью.
Флюидонасыщенная и газонасыщеннаятрещины
29. Флюидонасыщенная и газонасыщенная трещины
Коридор флюидонасыщенных вертикальных трещин30. Коридор флюидонасыщенных вертикальных трещин
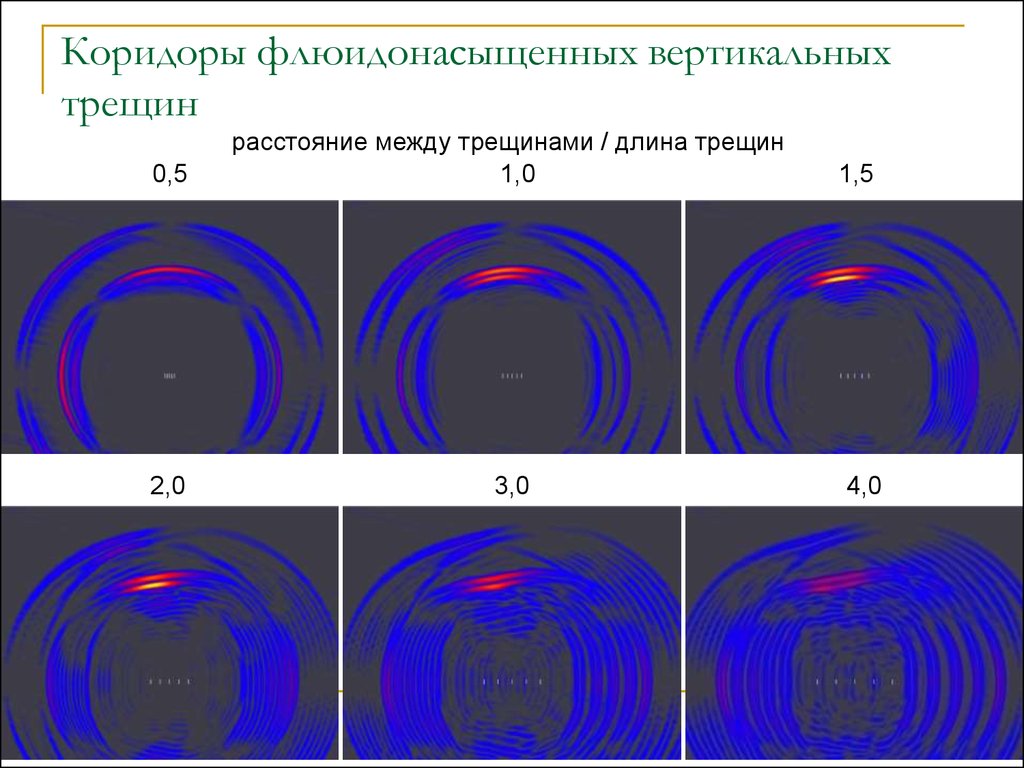
Коридоры флюидонасыщенных вертикальныхтрещин
0,5
расстояние между трещинами / длина трещин
1,0
2,0
3,0
1,5
4,0
31. Коридоры флюидонасыщенных вертикальных трещин
Двухслойная геологическая среда32. Двухслойная геологическая среда
Многослойная геологическая среда33. Многослойная геологическая среда
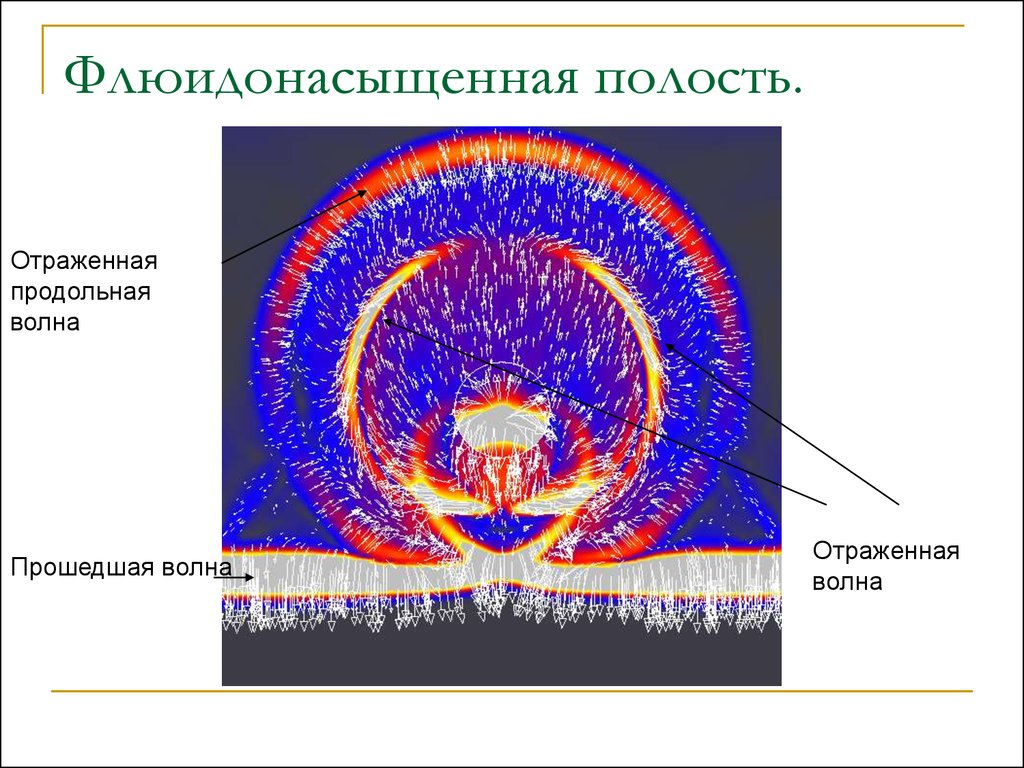
Флюидонасыщенная полость.Отраженная
продольная
волна
Прошедшая волна
Отраженная
волна
34. Флюидонасыщенная полость.
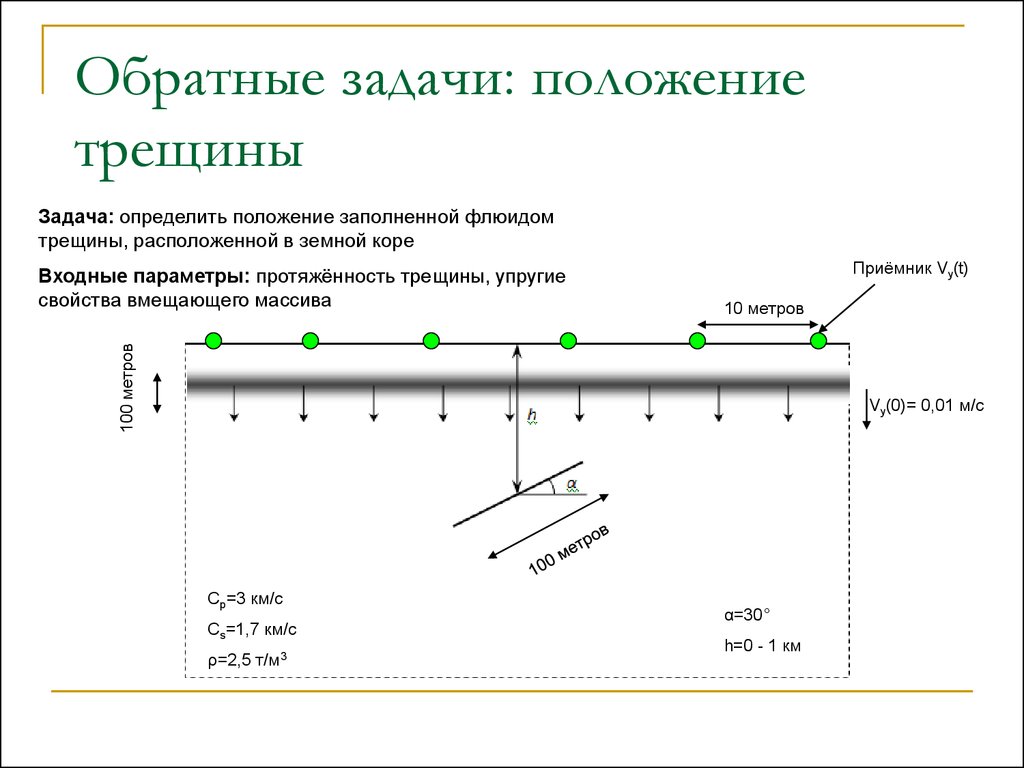
Обратные задачи: положениетрещины
Задача: определить положение заполненной флюидом
трещины, расположенной в земной коре
Приёмник Vy(t)
10 метров
100 метров
Входные параметры: протяжённость трещины, упругие
свойства вмещающего массива
Vy(0)= 0,01 м/с
Cp=3 км/с
Cs=1,7 км/c
ρ=2,5 т/м3
α=30°
h=0 - 1 км
35. Обратные задачи: положение трещины
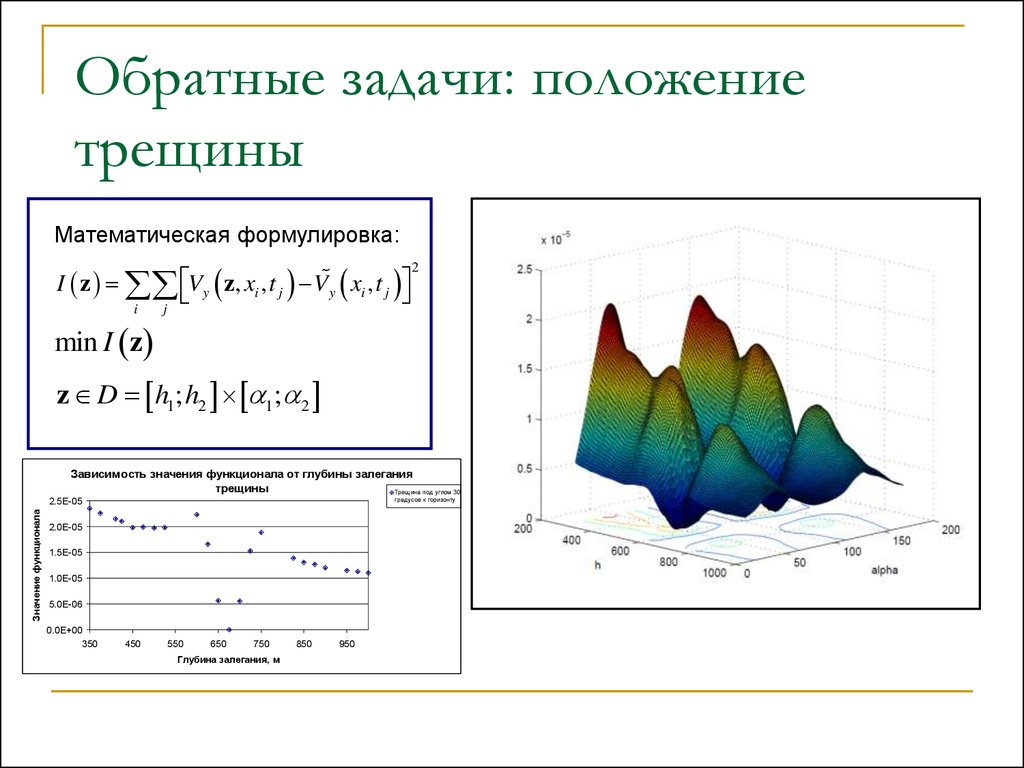
Математическая формулировка:I z Vy z, xi , t j Vy xi , t j
i
j
2
min I z
z D h1; h2 1; 2
Зависимость значения функционала от глубины залегания
трещины
Трещина под углом 30
Значение функционала
2.5E-05
градусов к горизонту
2.0E-05
1.5E-05
1.0E-05
5.0E-06
0.0E+00
350
450
550
650
750
Глубина залегания, м
850
950
36. Обратные задачи: положение трещины
Численное моделированиепоследствий природных и
техногенных катастроф.
37.
Возмущение из очага землетрясения: 3D38.
Волновые фронты вблизи дневной поверхности39.
Модель АЭС: двумерная постановкаМногокомпонентная
модель (Cp, Cs, ρ)
Возмущени
е:
P-wave
Рис. – Модуль скорости
40. Модель АЭС: двумерная постановка
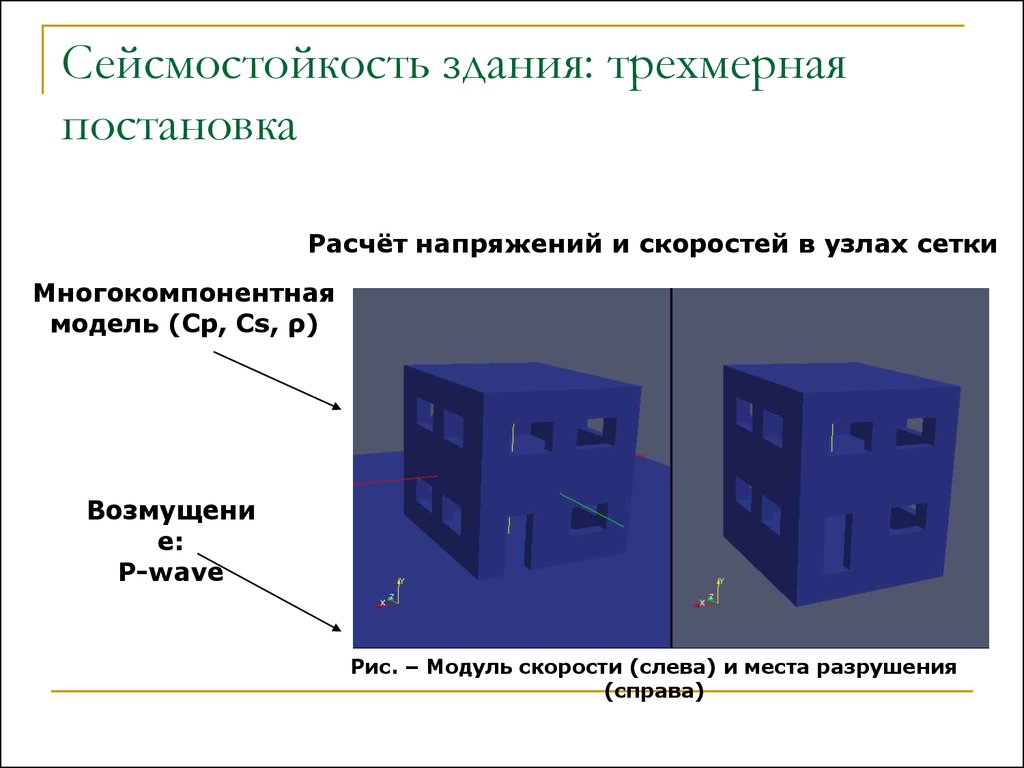
Сейсмостойкость здания: трехмернаяпостановка
Расчёт напряжений и скоростей в узлах сетки
Многокомпонентная
модель (Cp, Cs, ρ)
Возмущени
е:
P-wave
Рис. – Модуль скорости (слева) и места разрушения
(справа)
41. Сейсмостойкость здания: трехмерная постановка
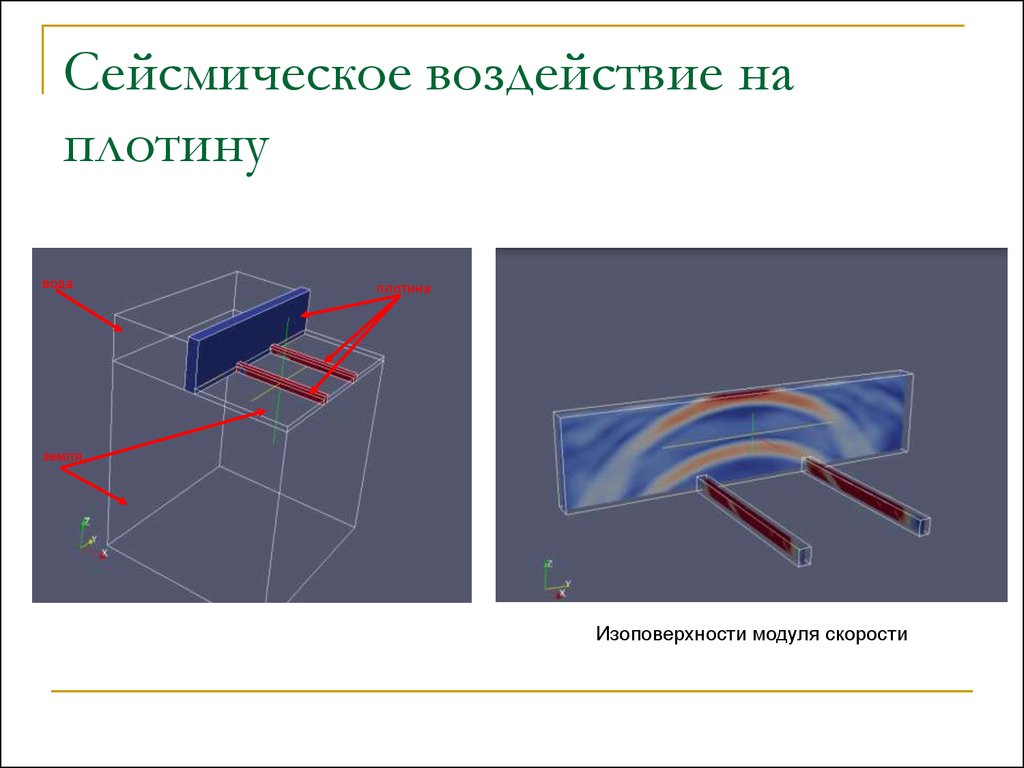
Сейсмическое воздействие наплотину
вода
плотина
земля
Изоповерхности модуля скорости
42. Сейсмическое воздействие на плотину
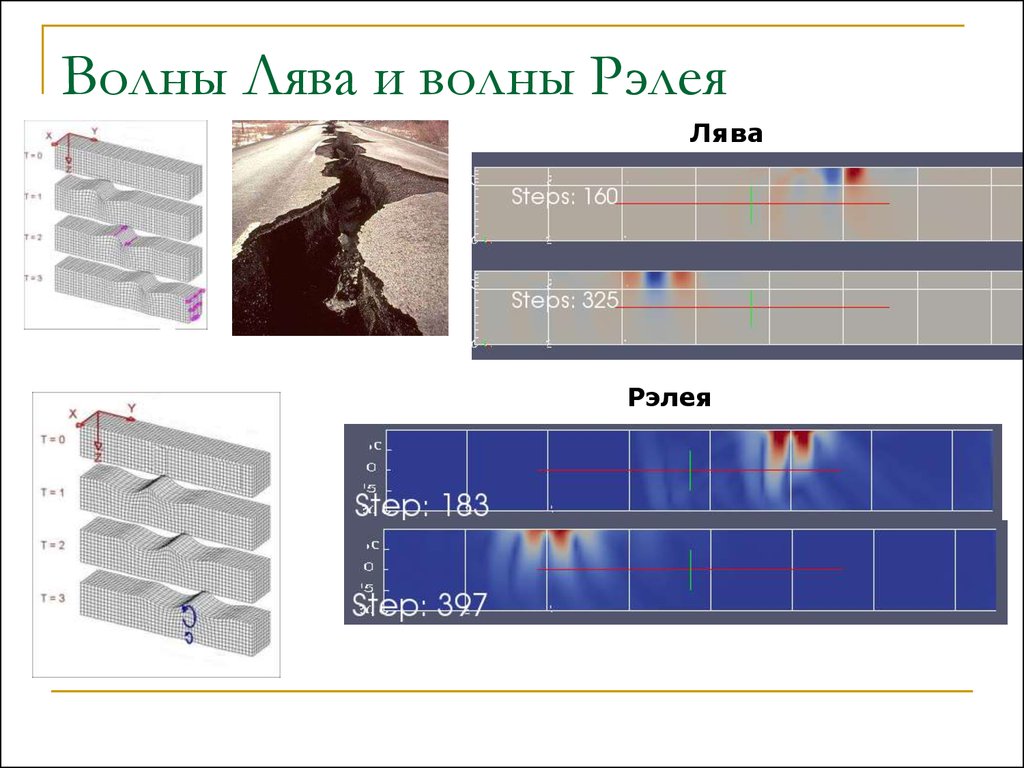
Волны Лява и волны РэлеяЛява
Рэлея
43. Волны Лява и волны Рэлея
Сравнение сейсмограмм землетрясения и взрыва44.
Задача о соударении с перфорированнойконструкцией
45. Задача о соударении с перфорированной конструкцией
46.
Задачи высокоскоростного соударения47. Задачи высокоскоростного соударения
48.
Задача о соударении с многослойной преградой49. Задача о соударении с многослойной преградой
50.
51.
52.
53.
54.
Численное моделированиесоударений сложных
конструкций.
55.
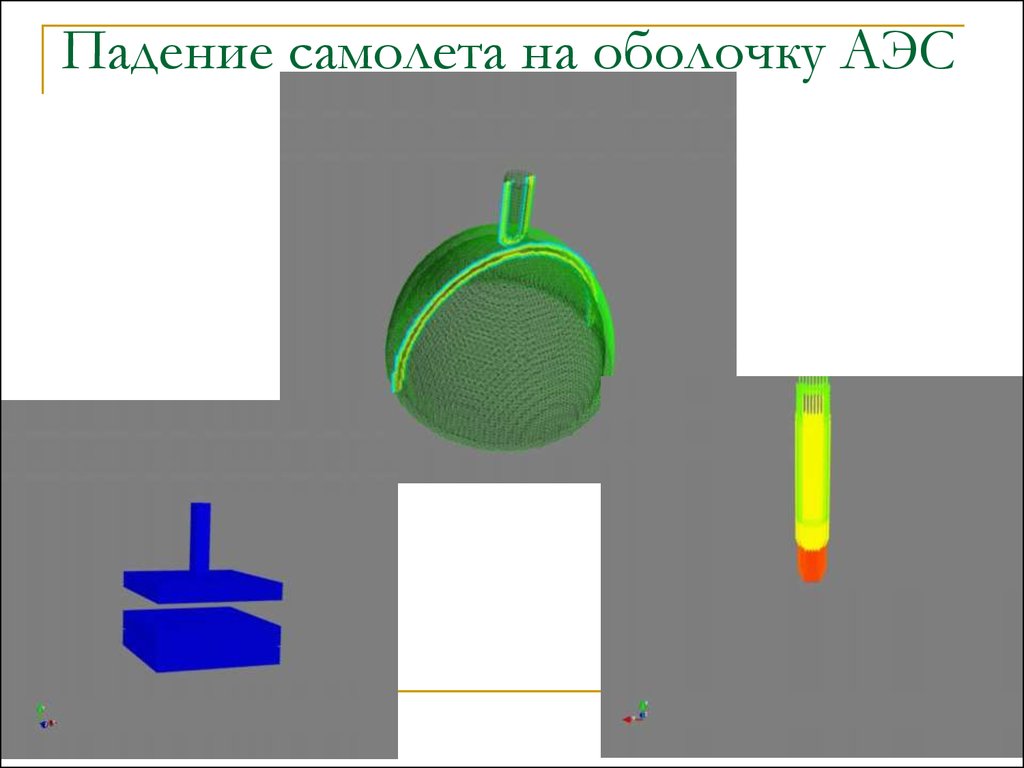
Падение самолета на оболочку АЭС56. Падение самолета на оболочку АЭС
Результаты численного эксперимента: соударение микрометеоритас двухслойной полусферической оболочкой и разнесенными
преградами
57.
Результаты численного эксперимента: соударение микрометеоритас 10 разнесенными преградами
58.
Постановка задачЗадача о наклонной посадке движущегося
подводного объекта на дно
Задача о соударении самолета с
деформируемой преградой и с движущимся
подводным объектом
Задача о соударении движущегося
подводного объекта с жесткой преградой
Задача о лобовом и перпендикулярном
столкновении движущихся подводных
объектов
Задача о соударении снаряда с
движущимся подводным объектом
Задача о соударении с
перфорированной конструкцией
59.
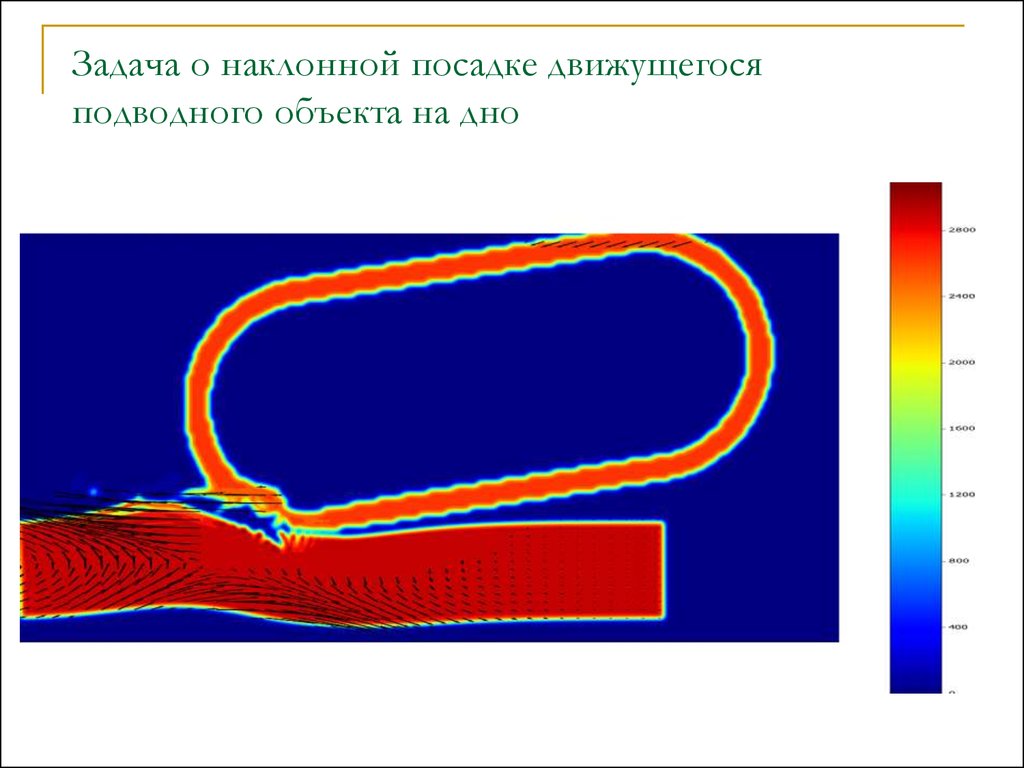
Задача о наклонной посадке движущегосяподводного объекта на дно
60. Задача о наклонной посадке движущегося подводного объекта на дно
Задача о соударении самолета с деформируемойпреградой.
Параметры фюзеляжа:
Длина: 15м
Внеш. радиус: 2м
Толщина стенок: 0.5м
λ = 80,3 ГПа
μ = 25,4 ГПа
ρ = 2740 кг/ м3
Е = 70 ГПа
Параметры преграды:
Толщина: 1м
Длина: 30м
λ = 80,3 ГПа
μ = 25,4 ГПа
ρ = 2740 кг/ м3
Е = 70 ГПа
Параметры двигателей:
Радиус: 2м
λ = 115,4 ГПа
μ = 77 ГПа
ρ = 7800 кг/ м3
Е = 200 ГПа
61. Задача о соударении самолета с деформируемой преградой.
Задача о соударении самолета с деформируемойпреградой
62. Задача о соударении самолета с деформируемой преградой
Численное решение задачдинамического контакта.
63.
Разбиение основной задачиПрогрев, воспламенение и горение пороха
Движение пороховых газов в
заснарядном объеме
Функционирование
дульных устройств
Движение снаряда по
каналу ствола
Гидрогазодинамика и
тепловое состояние
противооткатных устройств
Тепловое состояние ствола и
расчет устройств охлаждения
ствола
Задачи прочности и
динамики всех элементов
системы
64.
Расчётная сетка65. Расчётная сетка
66.
Цилиндр с хромированнойвнутренней поверхностью
Значения максимального главного напряжения. Изолинии демонстрируют
распространение волн вдоль поверхности цилиндра. Начало движения.
67. Цилиндр с хромированной внутренней поверхностью
Прочность трубопроводовДавление в трубе
вызывает деформации
и раскрытие трещины
Область коррозии трубы
























































 Программирование
Программирование Информатика
Информатика