Численные методы расчета переходных процессов (лекция № 20)

1. Лекция № 20

Лекционные презентации
«Численные методы
расчета переходных
процессов»
Лекция № 20
В лекции рассматривается методика
численного расчета переходных процессов
в линейных цепях, в том числе методом
дискретных схем замещения. Особое
внимание уделено понятиям «жестких» и
«дребезжащих» систем и особенностям их
анализа.
MП
каф. ТОЭ МЭИ 2016
1

2. Численные методы расчета переходных процессов

Лекция № 20
Численные методы расчета переходных
процессов
Состояние цепи после коммутации описывается линейной
системой дифференциальных уравнений:
x&= f (t , x) x(0)=x0
Аналитическое решение таких систем часто связано с
существенными трудностями.
Решение может быть найдено с использованием методов
численного интегрирования.
При использовании методов численного интегрирования
(метода Эйлера, трапеций и т.д.) дифференциальное уравнение
заменяется конечно-разностным уравнением:
dx xk - xk -1
»
, где h = dt – шаг интегрирования.
dt
h
MП
каф. ТОЭ МЭИ 2016
2

3. Численные методы расчета переходных процессов

Лекция № 20
Численные методы расчета переходных
процессов
Численное решение на интервале [ 0, t1 ] находят в виде таблицы
дискретных значений:
t
0
h
2h
…
x
x (0)
x ( h)
x (2h)
…
Nh = t1
x (t1 )
где h = dt – шаг интегрирования, tk = kh – дискретное время,
k = 0,1,K , N , N = t1 h – число шагов интегрирования;
x (tk ) » x(tk ) , x (0) = x(0)
MП
каф. ТОЭ МЭИ 2016
3

4. Методы численного интегрирования

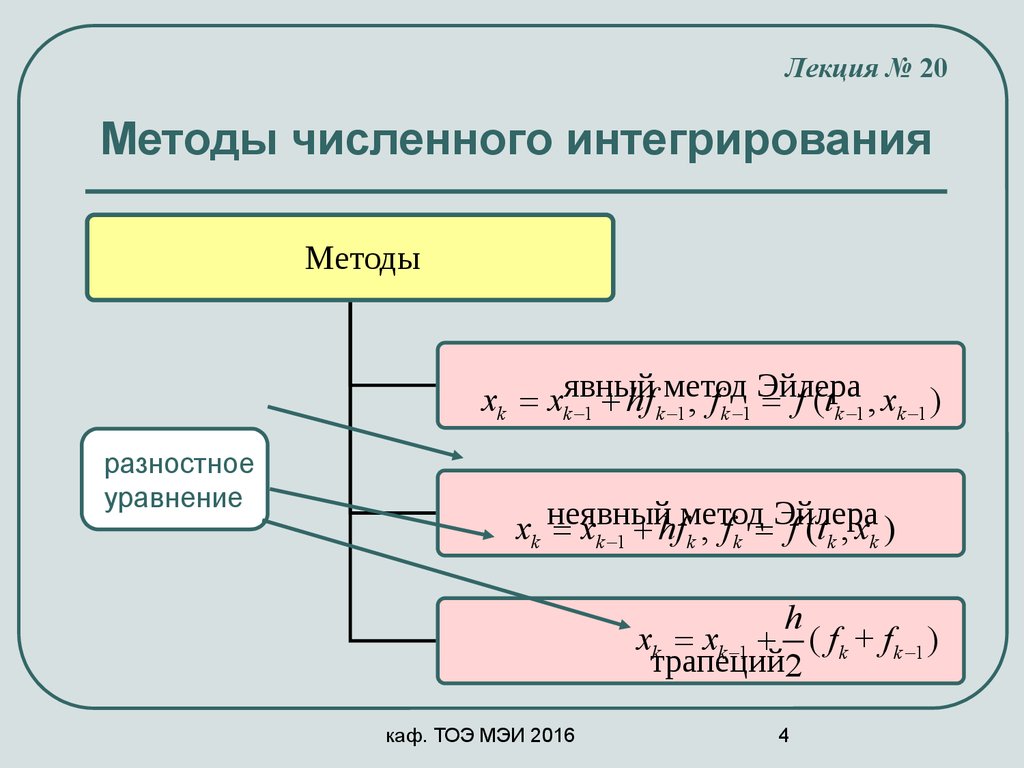
Лекция № 20
Методы численного интегрирования
Методы
метод
Эйлера
xk = xkявный
+
hf
,
f
-1
k -1
k -1 = f (t k -1 , xk -1 )
разностное
уравнение
Эйлера
xk неявный
= xk -1 + hfметод
,
f
=
f (tk , xk )
k
k
h
xk = xk -1 + ( f k + f k -1 )
трапеций2
каф. ТОЭ МЭИ 2016
4

5. Пример расчета переходного процесса численным методом

Лекция № 20
Пример расчета переходного процесса
численным методом
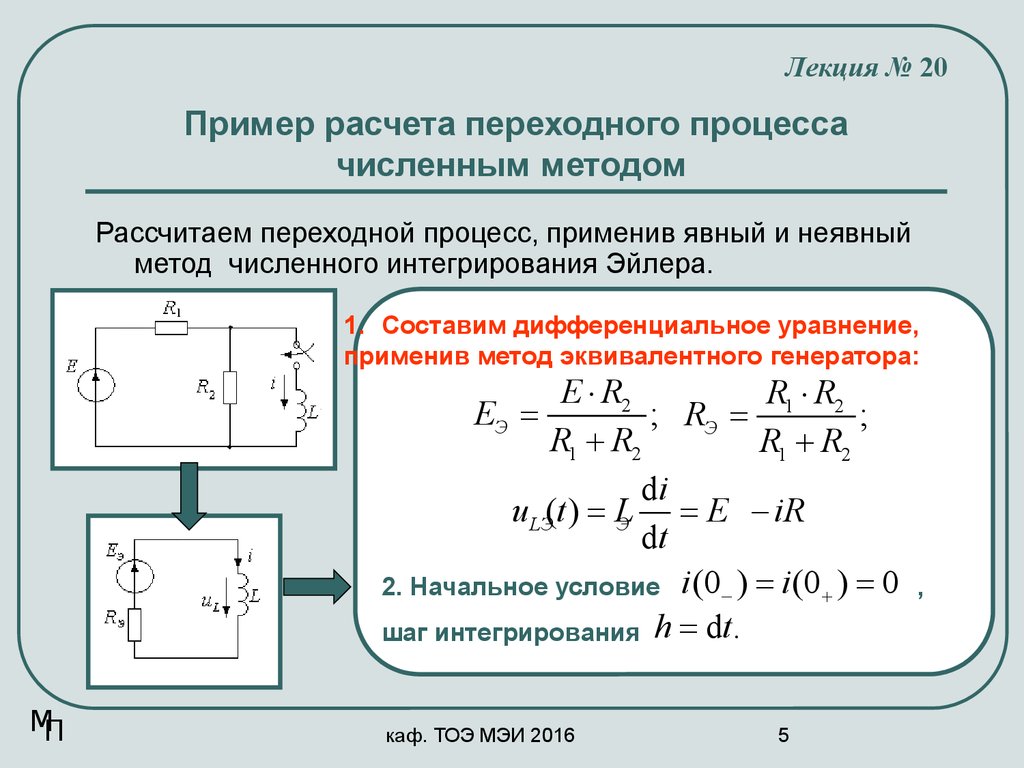
Рассчитаем переходной процесс, применив явный и неявный
метод численного интегрирования Эйлера.
1. Составим дифференциальное уравнение,
применив метод эквивалентного генератора:
E × R2
R1 × R2
EЭ =
; RЭ =
;
R1 + R2
R1 + R2
di
uLЭ(t ) = L
= E - iR
Э
dt
2. Начальное условие i (0 - ) = i (0 + ) = 0
шаг интегрирования h = dt .
MП
каф. ТОЭ МЭИ 2016
5
,

6. Пример расчета переходного процесса численным методом

Лекция № 20
Пример расчета переходного процесса
численным методом
Рассчитаем переходной процесс, применив явный и неявный
метод численного интегрирования Эйлера.
3. Составим разностное уравнение:
di ik - ik -1
=
dt
h
ik - ik -1 1
= ( EЭ - ik -1RЭ )
h
L
h
ikЭ= k ( E Э - i -k1 R ) + i -1 при k = 1 i0 = 0
L
ik - ik -1 1
= ( EЭ - ik RЭ )
Явный метод Эйлера:
h
L
hEЭ
hRЭ
ik = (
+ ik -1 ) (1 +
) при k = 1 i0 = 0
L
L
Неявный метод Эйлера:
MП
каф. ТОЭ МЭИ 2016
6

7. Пример расчета переходного процесса численным методом

Лекция № 20
Пример расчета переходного процесса
численным методом
Результаты численного интегрирования для h = 0,5t
параметры
элементов цепи:
E = 50 В
L = 0,02 Гн
R1 = 10 Ом
R2 = 40 Ом
MП
каф. ТОЭ МЭИ 2016
ik
tk = k × h
7
ik

8. Пример расчета переходного процесса численным методом

Лекция № 20
Пример расчета переходного процесса
численным методом
Результаты численного интегрирования для
параметры
элементов цепи:
E = 50 В
L = 0,02 Гн
R1 = 10 Ом
R2 = 40 Ом
MП
каф. ТОЭ МЭИ 2016
h = 0,1t
ik
tk = k × h
8
ik

9. Пример расчета переходного процесса численным методом

Лекция № 20
Пример расчета переходного процесса
численным методом
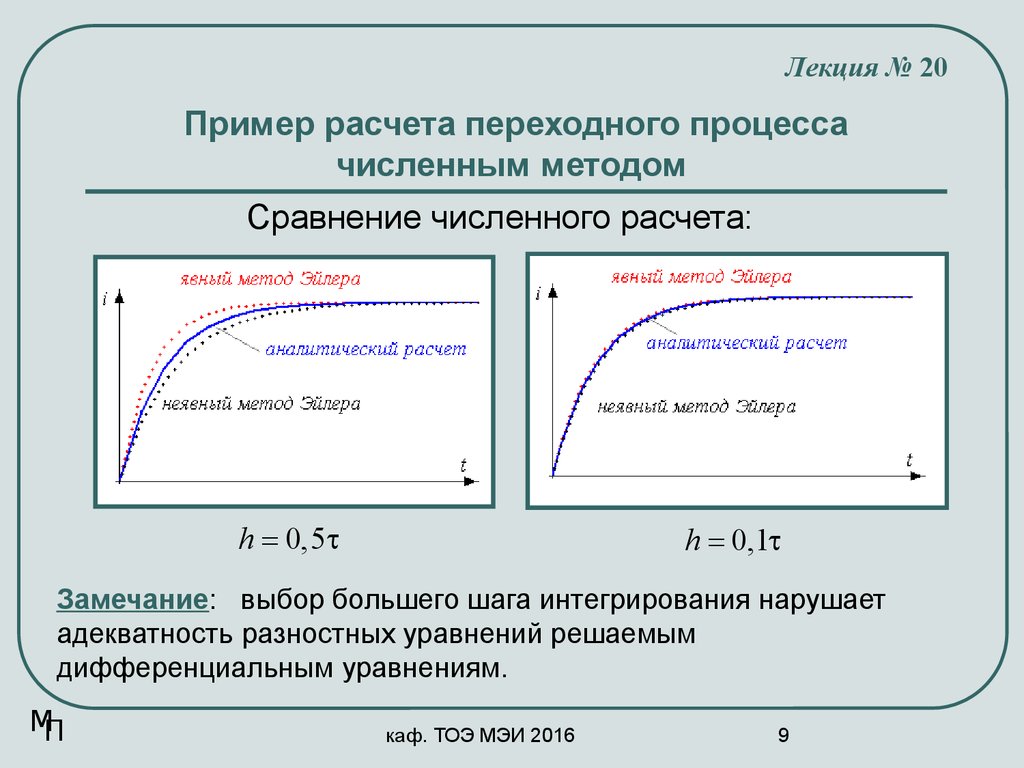
Сравнение численного расчета:
h = 0,5t
h = 0,1t
Замечание: выбор большего шага интегрирования нарушает
адекватность разностных уравнений решаемым
дифференциальным уравнениям.
MП
каф. ТОЭ МЭИ 2016
9

10. Метод дискретных схем замещения

Лекция № 20
Метод дискретных схем замещения
При замене дифференциальных уравнений конечно-разностными
уравнениями используют чисто резистивные схемы замещения.
Реактивные элементы заменяют дискретными моделями.
x&= f (t , x) x(0)=x0
dx xk - xk -1
x&=
»
dt
h
где h = dt - шаг интегрирования
Неявный метод Эйлера
xk = xk -1 + hf (tk , xk )
MП
каф. ТОЭ МЭИ 2016
10

11. Дискретная модель индуктивного элемента

Лекция № 20
Дискретная модель индуктивного
элемента
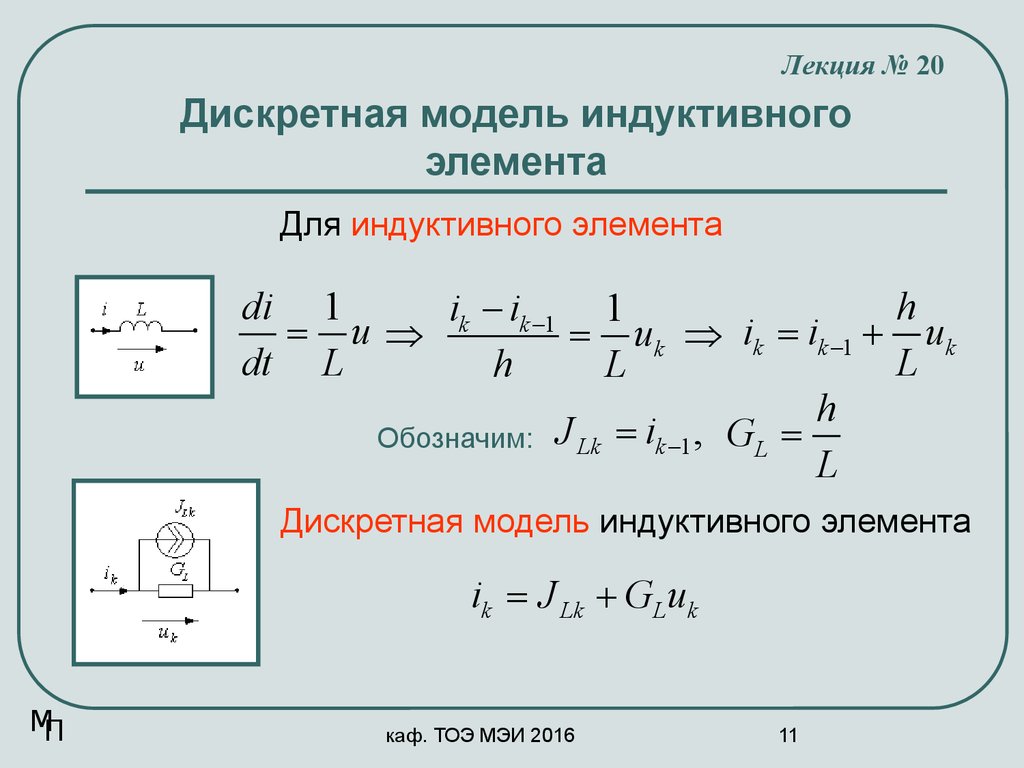
Для индуктивного элемента
di 1
h
ik - ik -1 1
= uÞ
= uk Þ ik = ik -1 + uk
dt L
L
h
L
h
Обозначим: J Lk = ik -1 , GL =
L
Дискретная модель индуктивного элемента
ik = J Lk + GLuk
MП
каф. ТОЭ МЭИ 2016
11

12. Дискретная модель емкостного элемента

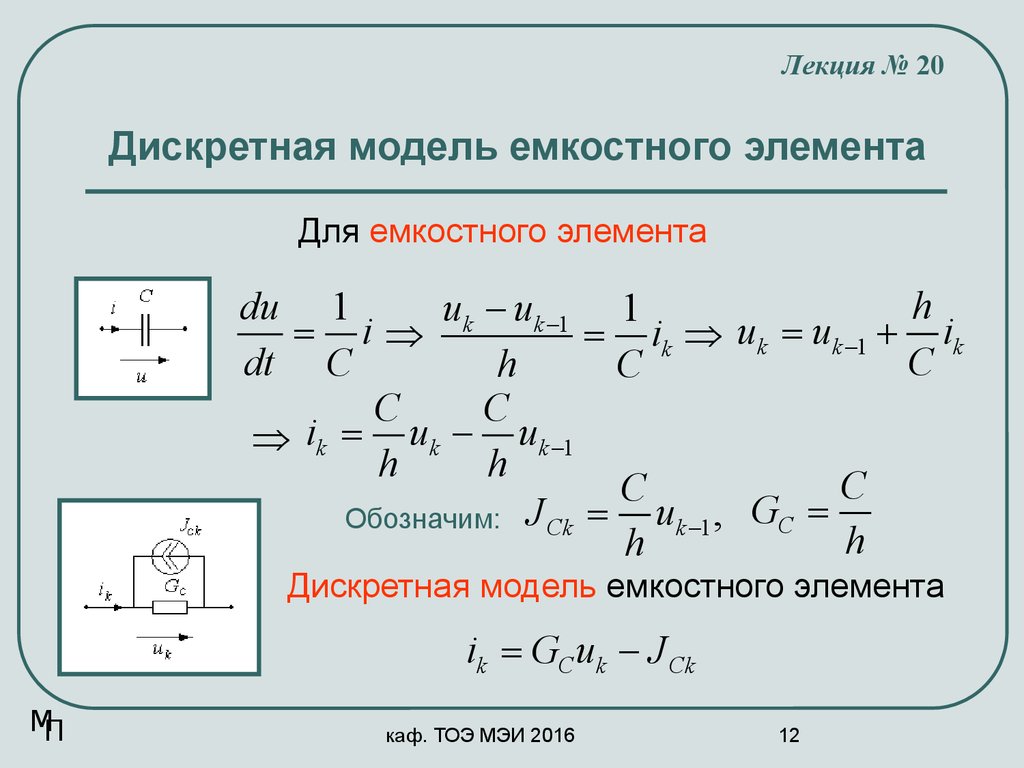
Лекция № 20
Дискретная модель емкостного элемента
Для емкостного элемента
h
du 1
uk - uk -1 1
= iÞ
= ik Þ uk = uk -1 + ik
C
dt C
h
C
C
C
Þ ik = uk - uk -1
h
h
C
C
uk -1 , GC =
Обозначим: J Ck =
h
h
Дискретная модель емкостного элемента
ik = GC uk - J Ck
MП
каф. ТОЭ МЭИ 2016
12

13. Пример расчета переходного процесса методом дискретных схем замещения

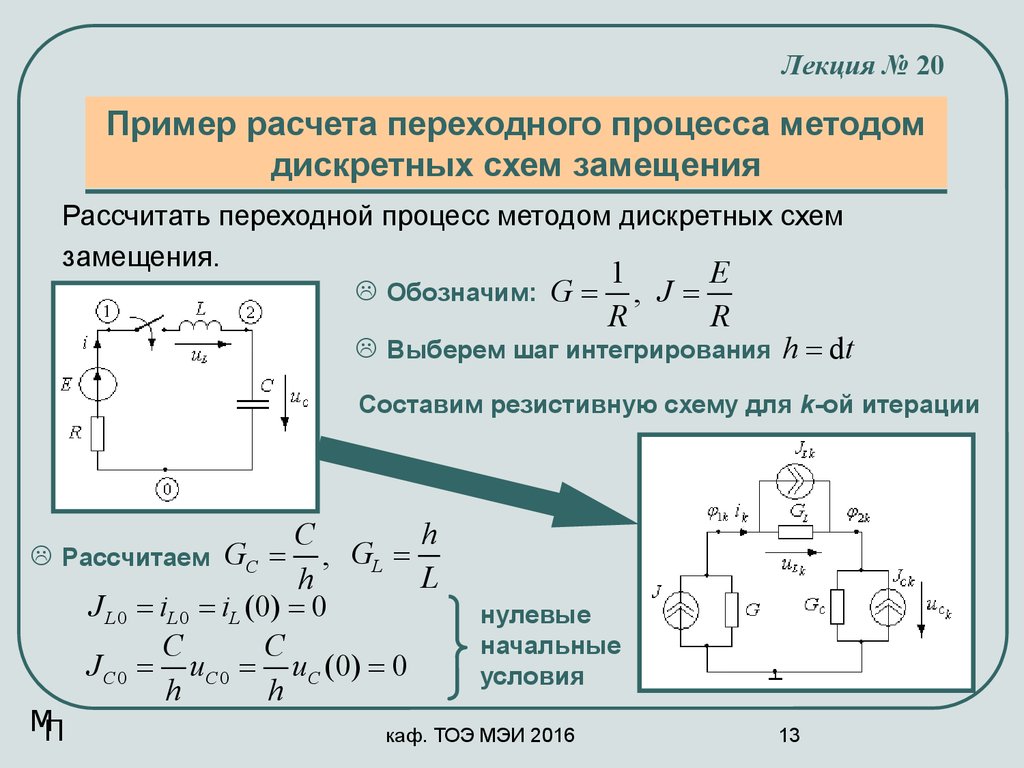
Лекция № 20
Пример расчета переходного процесса методом
дискретных схем замещения
Рассчитать переходной процесс методом дискретных схем
замещения.
Обозначим:
1
E
G= , J =
R
R
Выберем шаг интегрирования
h = dt
Составим резистивную схему для k-ой итерации
h
C
Рассчитаем GC = , GL =
L
h
J L 0 = iL 0 = iL (0) = 0
C
C
J C 0 = uC 0 = uC (0) = 0
h
h
MП
нулевые
начальные
условия
каф. ТОЭ МЭИ 2016
13

14. Пример расчета переходного процесса методом дискретных схем замещения

Лекция № 20
Пример расчета переходного процесса методом
дискретных схем замещения
Методом узловых потенциалов (напряжений) рассчитаем на k-ой
итерации потенциалыj1k
jи2k
éG + GL
ê -G
L
ë
:
-GL ù é j1k ù é J - J Lk ù
=ê
ú
ê
ú
GL + GC û ëj2 k û ë J Lk + J Ck úû
Для тока и напряжений на реактивных
элементах на k-ой итерации:
ik = J Lk + GL (j1k - j2 k )
uCk = j2 k
uLk = j1k - j2 k
MП
каф. ТОЭ МЭИ 2016
14

15. Замечания

Лекция № 20
Замечания
• Подобные резистивные схемы синтезируют топологические
особенности электрических цепей с численными методами
интегрирования, их называют синтетические. Синтетические
схемы используют также для расчета переходных процессов в
нелинейных цепях, позволяя выбрать переменные,
обеспечивающие однозначное решение.
• При использовании численных методов возникает вопрос
адекватности получаемого численного решения истинному
решению уравнений, сходимости и устойчивости.
MП
каф. ТОЭ МЭИ 2016
15

16. «Жёсткие» и «дребезжащие» модели электрических цепей

Лекция № 20
«Жёсткие» и «дребезжащие» модели
электрических цепей
• При составлении математических моделей
электродинамических систем и электрических цепей необходимо
в первую очередь учитывать факторы, играющие
первостепенную роль в моделируемом процессе.
• Без учета особенностей численная обработка (например, выбор
шага интегрирования) становится весьма сложной. В этом
отношении два типа моделей – «жесткие» и «дребезжащие»
модели типичны для задач теории электрических цепей.
• Такие модели цепей весьма часто встречаются на практике,
методы физического и математического их исследования весьма
актуальны для современного инженера.
MП
каф. ТОЭ МЭИ 2016
16

17. Пример, иллюстрирующий явление «жесткости»

Лекция № 20
Пример, иллюстрирующий явление «жесткости»
При моделировании процесса разрядки конденсатора на RL-цепь
была составлена схема и уравнение , описывающее состояние
цепи после коммутации.
d 2i
di 1
L 2 +R + i=0
dt
dt C
Характеристическое уравнение:
p 2 + 2 ×1010 p + 2 ×1011 = 0
R
p1 » -2 ×10 = L
1
p2 » -10 = RC
10
Корни уравнения:
MП
каф. ТОЭ МЭИ 2016
Отношение модулей корней
p1
: 1010
p2
17

18. «Жёсткие» системы, уравнения и модели электрических цепей

Лекция № 20
«Жёсткие» системы, уравнения и модели
электрических цепей
Жесткими называют системы (математические модели, уравнения
цепей), траектории процессов которых имеют два выраженных
участка:
• участок пограничного слоя t Î [ 0, tпс ] с большой скоростью
процессов (большими по модулю значениями производных
переходных токов, напряжений и т.д.);
• участок t Î [ tпс , t1 ] , tпс = t1.
Здесь tпс - длительность пограничного слоя, t1 - заданное время
исследования.
Длительность пограничного слоя можно определить как ( 3 ¸ 5 ) tmin
гдеtmin - минимальная постоянная времени цепи.
MП
каф. ТОЭ МЭИ 2016
18

19. Пример, иллюстрирующий явление «жесткости»

Лекция № 20
Пример, иллюстрирующий явление «жесткости»
В решении переходного процесса два вида функций:
быстроубывающая с большой производной и функция с малой
производной.
Длительность пограничного слоя
( 3 ¸ 5) tmin = ( 3 ¸ 5)
tпс
1
L
= ( 3 ¸ 5)
p1
R
Участок пограничного слоя характеризуется быстрым изменением тока при
практически неизменном напряжении
на конденсаторе
После прохождения пограничного слоя ток плавно спадает до нуля
практически за время t1 = ( 3 ¸ 5 ) t max = ( 3 ¸ 5 )
1
= ( 3 ¸ 5 ) RC
p2
Индуктивность катушки не оказывает влияния на характер процесса
MП
каф. ТОЭ МЭИ 2016
19

20. Разделение процессов с существенно разными скоростями

Лекция № 20
Разделение процессов с существенно разными
скоростями
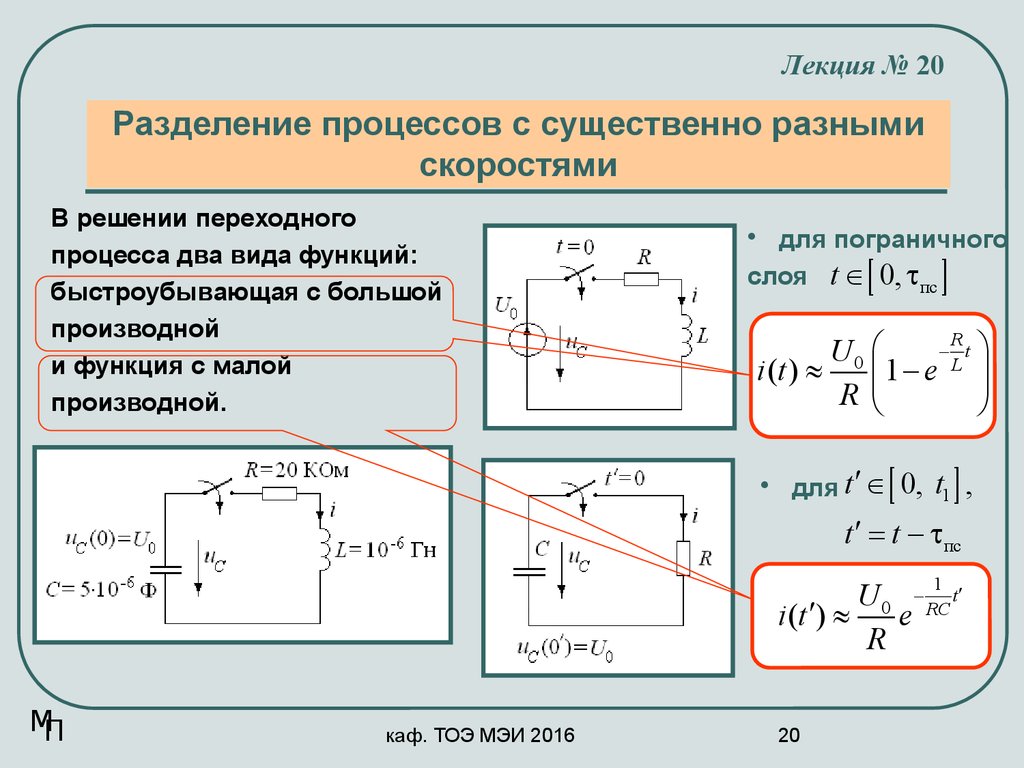
В решении переходного
процесса два вида функций:
быстроубывающая с большой
производной
и функция с малой
производной.
• для пограничного
слоя t Î 0, tпс
[
]
R
- t ö
U0 æ
L
i (t ) »
ç1 - e ÷
Rè
ø
• для t ¢ Î
[ 0, t1 ] ,
t ¢ = t - tпс
1
t¢
U 0 - RC
i (t ¢) »
e
R
MП
каф. ТОЭ МЭИ 2016
20

21. Замечания

Лекция № 20
Замечания
Если проблема жесткости аналитически решается разделением
процессов с существенно разными скоростями, то численное
решение жесткого уравнения сталкивается со значительными
трудностями. Прежде всего, в выборе шага интегрирования,
который должен обеспечивать и точность решения и устойчивость.
Использование шага h1 = 0,5tmin = 0, 25 ×10-10сек,
обеспечивающего локальную точность, потребовало бы более
5 млрд. шагов и соответственно огромных затрат машинного
времени.
1
Использование шага h2 = 0,5tmax = 0,5 ×10 -сек
не обеспечило
бы локальной точности расчета (например, максимального
значения переходного тока).
MП
каф. ТОЭ МЭИ 2016
21

22. «Дребезжащие» системы, уравнения и модели электрических цепей

Лекция № 20
«Дребезжащие» системы, уравнения и модели
электрических цепей
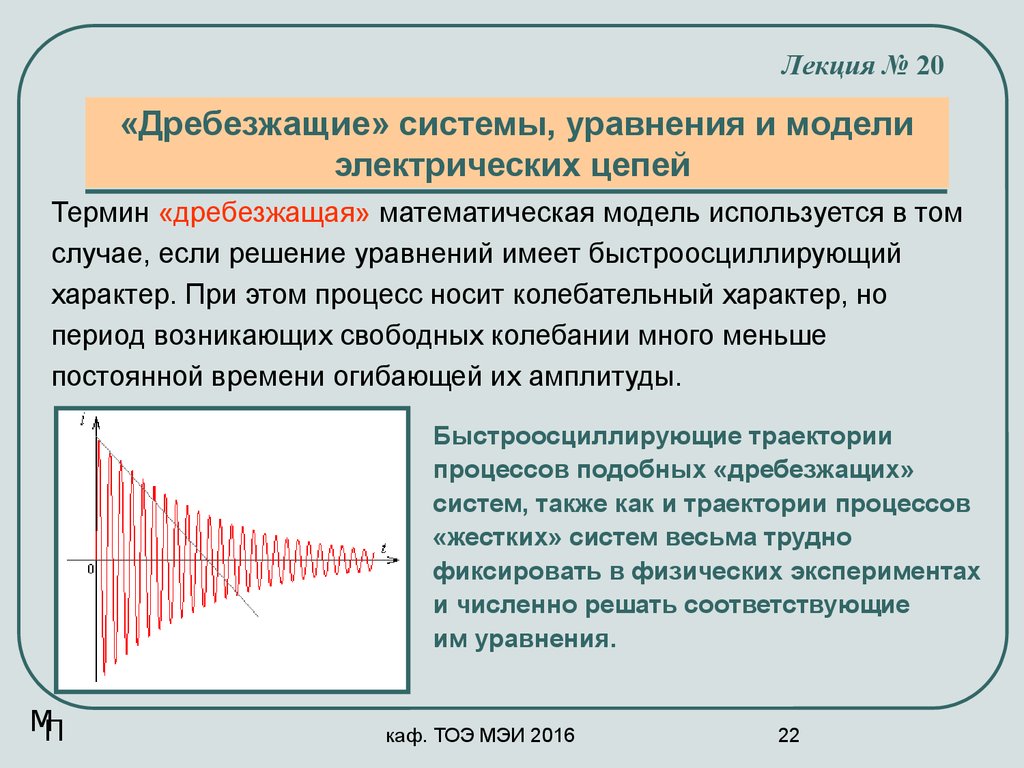
Термин «дребезжащая» математическая модель используется в том
случае, если решение уравнений имеет быстроосциллирующий
характер. При этом процесс носит колебательный характер, но
период возникающих свободных колебании много меньше
постоянной времени огибающей их амплитуды.
Быстроосциллирующие траектории
процессов подобных «дребезжащих»
систем, также как и траектории процессов
«жестких» систем весьма трудно
фиксировать в физических экспериментах
и численно решать соответствующие
им уравнения.
MП
каф. ТОЭ МЭИ 2016
22