Похожие презентации:
Кристаллография. История развития
1.
Лекция № 3.Кристаллография
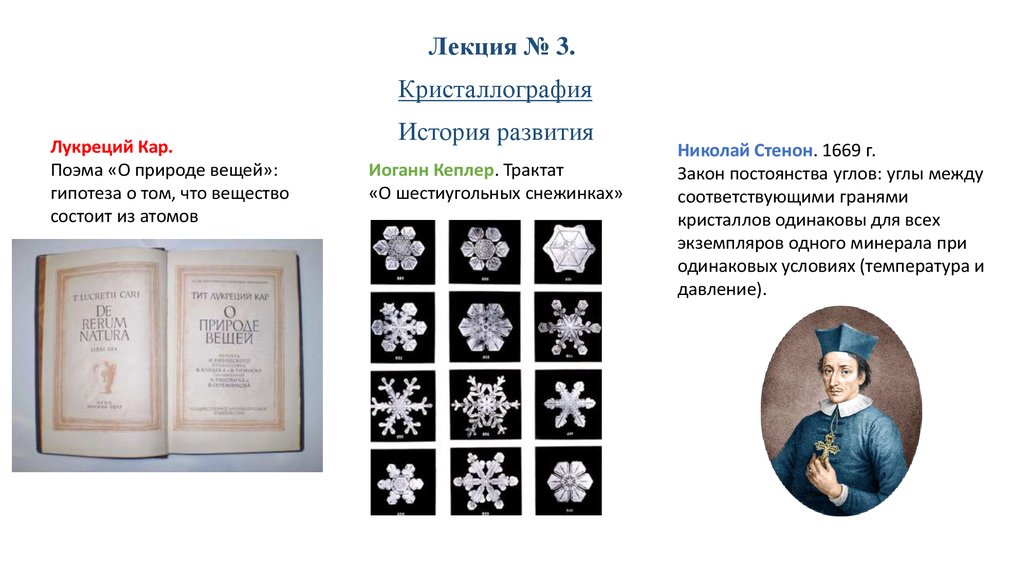
Лукреций Кар.
Поэма «О природе вещей»:
гипотеза о том, что вещество
состоит из атомов
История развития
Иоганн Кеплер. Трактат
«О шестиугольных снежинках»
Николай Стенон. 1669 г.
Закон постоянства углов: углы между
соответствующими гранями
кристаллов одинаковы для всех
экземпляров одного минерала при
одинаковых условиях (температура и
давление).
2.
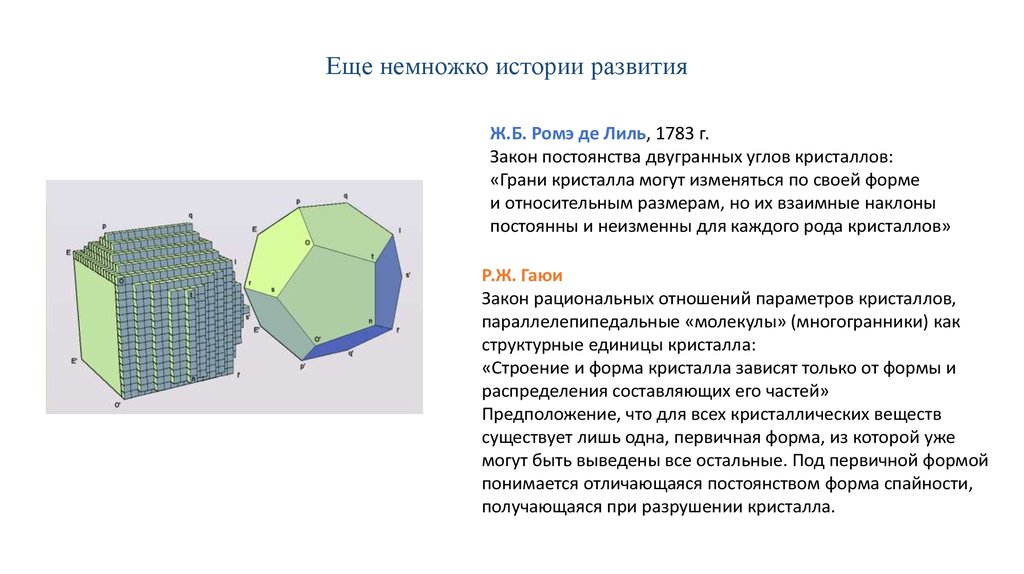
Еще немножко истории развитияЖ.Б. Ромэ де Лиль, 1783 г.
Закон постоянства двугранных углов кристаллов:
«Грани кристалла могут изменяться по своей форме
и относительным размерам, но их взаимные наклоны
постоянны и неизменны для каждого рода кристаллов»
Р.Ж. Гаюи
Закон рациональных отношений параметров кристаллов,
параллелепипедальные «молекулы» (многогранники) как
структурные единицы кристалла:
«Строение и форма кристалла зависят только от формы и
распределения составляющих его частей»
Предположение, что для всех кристаллических веществ
существует лишь одна, первичная форма, из которой уже
могут быть выведены все остальные. Под первичной формой
понимается отличающаяся постоянством форма спайности,
получающаяся при разрушении кристалла.
3.
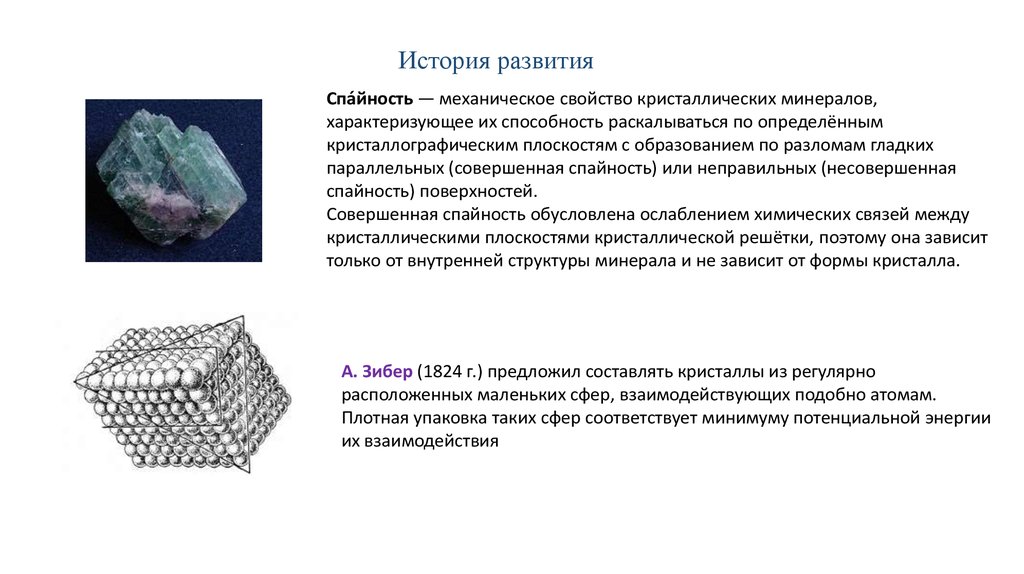
История развитияСпа́йность — механическое свойство кристаллических минералов,
характеризующее их способность раскалываться по определённым
кристаллографическим плоскостям с образованием по разломам гладких
параллельных (совершенная спайность) или неправильных (несовершенная
спайность) поверхностей.
Совершенная спайность обусловлена ослаблением химических связей между
кристаллическими плоскостями кристаллической решётки, поэтому она зависит
только от внутренней структуры минерала и не зависит от формы кристалла.
А. Зибер (1824 г.) предложил составлять кристаллы из регулярно
расположенных маленьких сфер, взаимодействующих подобно атомам.
Плотная упаковка таких сфер соответствует минимуму потенциальной энергии
их взаимодействия
4.
История развитияОгюст Браве. 1855 г.
Вывод 14 типов
пространственных решеток
Евграф Степанович Федоров
Артур Шенфлис
Вывод 230 пространственных групп симметрии
кристаллов
5.
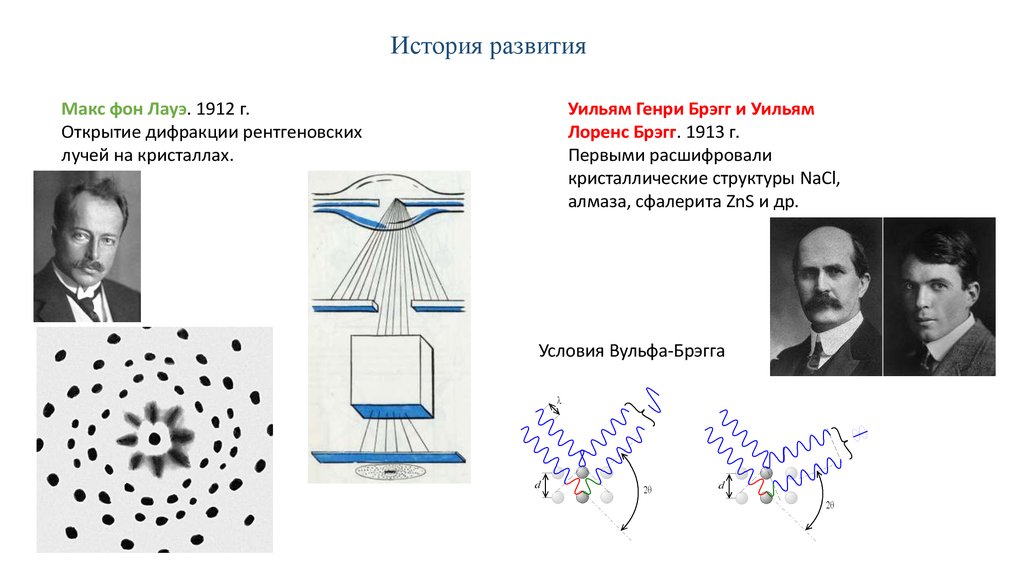
История развитияМакс фон Лауэ. 1912 г.
Открытие дифракции рентгеновских
лучей на кристаллах.
Уильям Генри Брэгг и Уильям
Лоренс Брэгг. 1913 г.
Первыми расшифровали
кристаллические структуры NaCl,
алмаза, сфалерита ZnS и др.
Условия Вульфа-Брэгга
6.
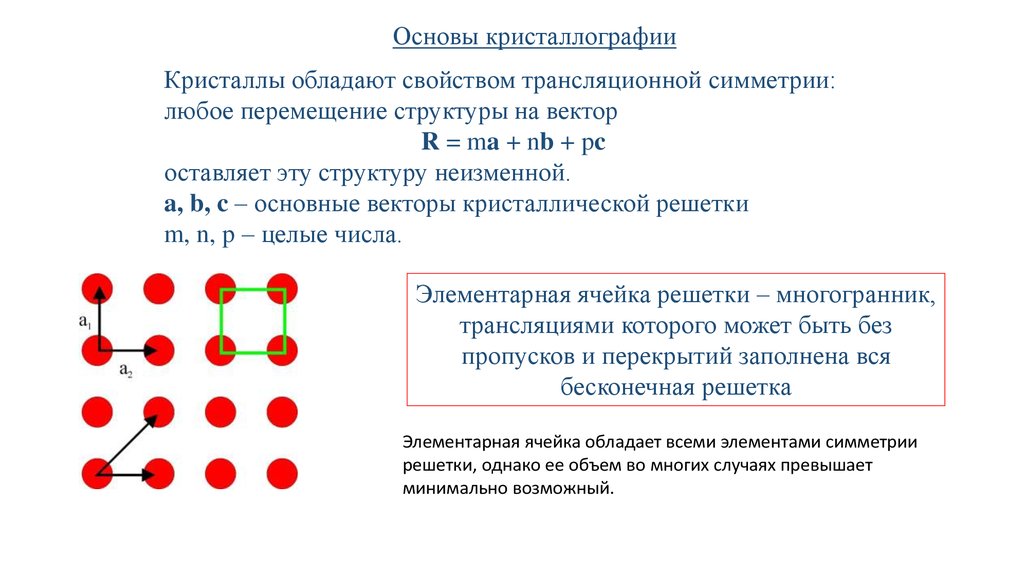
Основы кристаллографииКристаллы обладают свойством трансляционной симметрии:
любое перемещение структуры на вектор
R = ma + nb + pc
оставляет эту структуру неизменной.
a, b, c – основные векторы кристаллической решетки
m, n, p – целые числа.
Элементарная ячейка решетки – многогранник,
трансляциями которого может быть без
пропусков и перекрытий заполнена вся
бесконечная решетка
Элементарная ячейка обладает всеми элементами симметрии
решетки, однако ее объем во многих случаях превышает
минимально возможный.
7.
Базис решеткиСовокупность атомов одного элемента
элементарной ячейки – базис решетки
Пространственная решетка
С каждой точкой решетки мы связываем
группу атомов– базис решетки, причем
все группы идентичны по составу,
расположению и ориентации
Базис, содержащий
два различных иона
Кристаллическая структура
8.
Решетка БравэЕсли в кристалле имеются атомы лишь одного типа, то они находятся в узлах решетки. Такая
решетка называется решеткой Бравэ. Если имеется несколько типов атомов, то каждому
узлу соответствует группа из нескольких атомов. Они образуют базис решетки. В таком случае
говорят о решетке
с базисом.
Вершины параллелепипедов,
образующих элементарную ячейку - узлы Браве.
Точки решетки Бравэ, лежащие ближе всего к данной точке,
называются ее ближайшими соседями.
Координационное число – число ближайших соседей.
9.
Условнаяэлементарная
ячейка
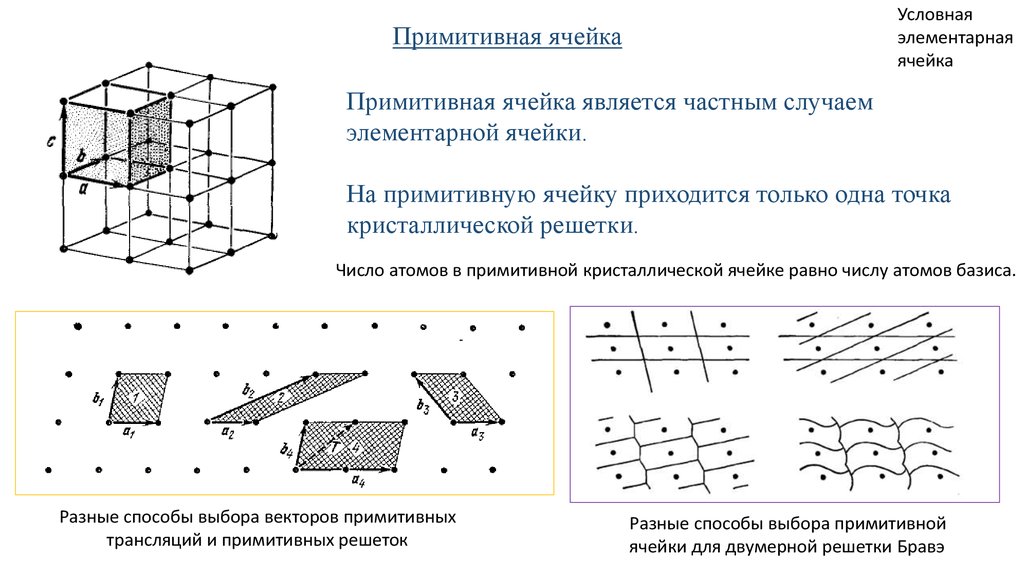
Примитивная ячейка
Примитивная ячейка является частным случаем
элементарной ячейки.
На примитивную ячейку приходится только одна точка
кристаллической решетки.
Число атомов в примитивной кристаллической ячейке равно числу атомов базиса.
Разные способы выбора векторов примитивных
трансляций и примитивных решеток
Разные способы выбора примитивной
ячейки для двумерной решетки Бравэ
10.
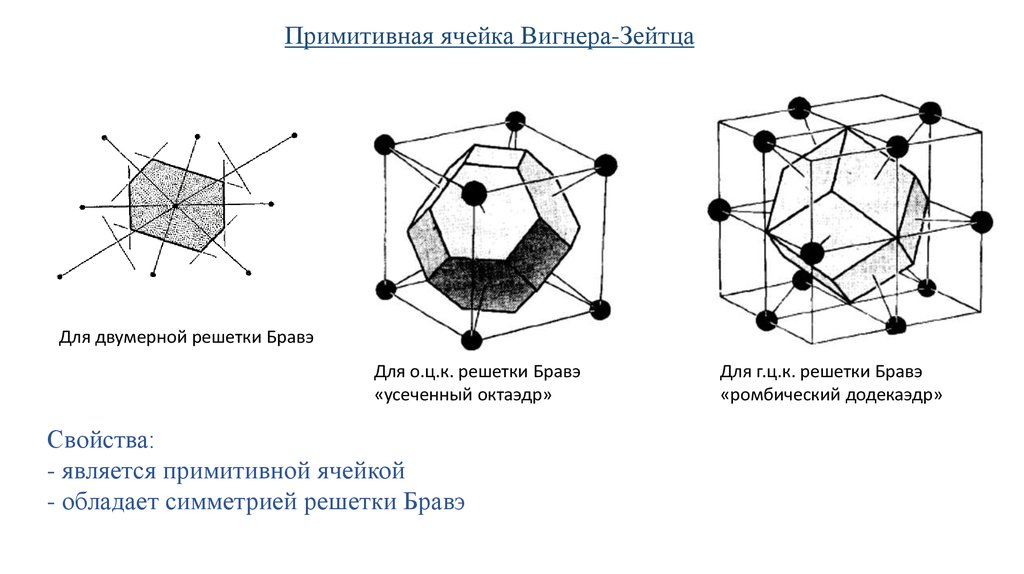
Примитивная ячейка Вигнера-ЗейтцаДля двумерной решетки Бравэ
Для о.ц.к. решетки Бравэ
«усеченный октаэдр»
Свойства:
- является примитивной ячейкой
- обладает симметрией решетки Бравэ
Для г.ц.к. решетки Бравэ
«ромбический додекаэдр»
11.
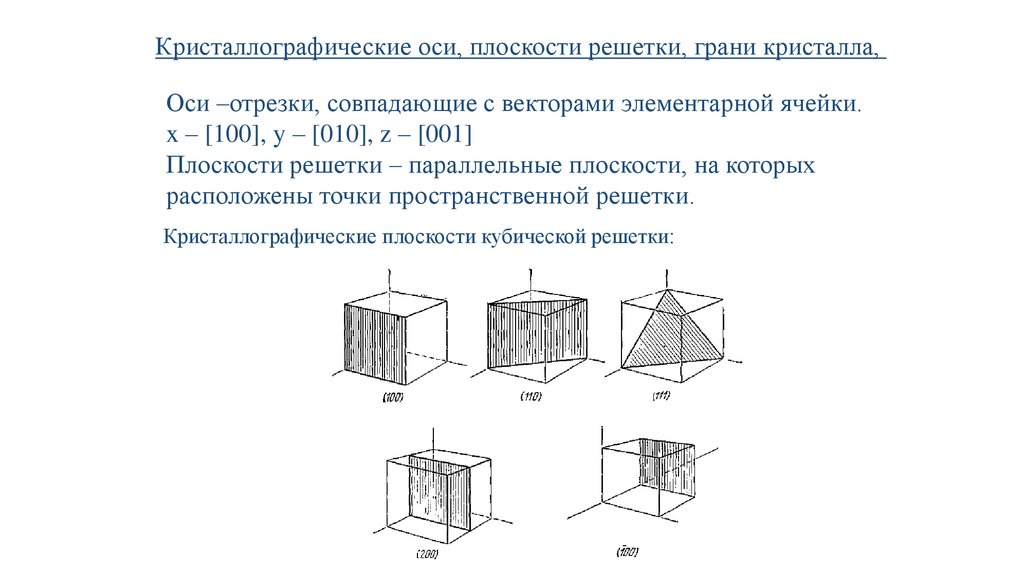
Кристаллографические оси, плоскости решетки, грани кристалла,Оси –отрезки, совпадающие с векторами элементарной ячейки.
x – [100], y – [010], z – [001]
Плоскости решетки – параллельные плоскости, на которых
расположены точки пространственной решетки.
Кристаллографические плоскости кубической решетки:
12.
Грани кристалла параллельны плоскостям,отсекающим на трех осях отрезки a/p, b/q, c/r
(p, q, r – целые числа)
Индексы, определяющие грань кристалла – индексы Миллера
(p q r) и (
) - две параллельные грани на противоположных
сторонах кристалла
Грань, параллельная оси, имеет индекс 0.





 Химия
Химия








