Свойства медиан и биссектрисы треугольника

1.

ТЕОРЕМА О МЕДИАНЕ.
ТЕОРЕМА О БИССЕКТРИСЕ

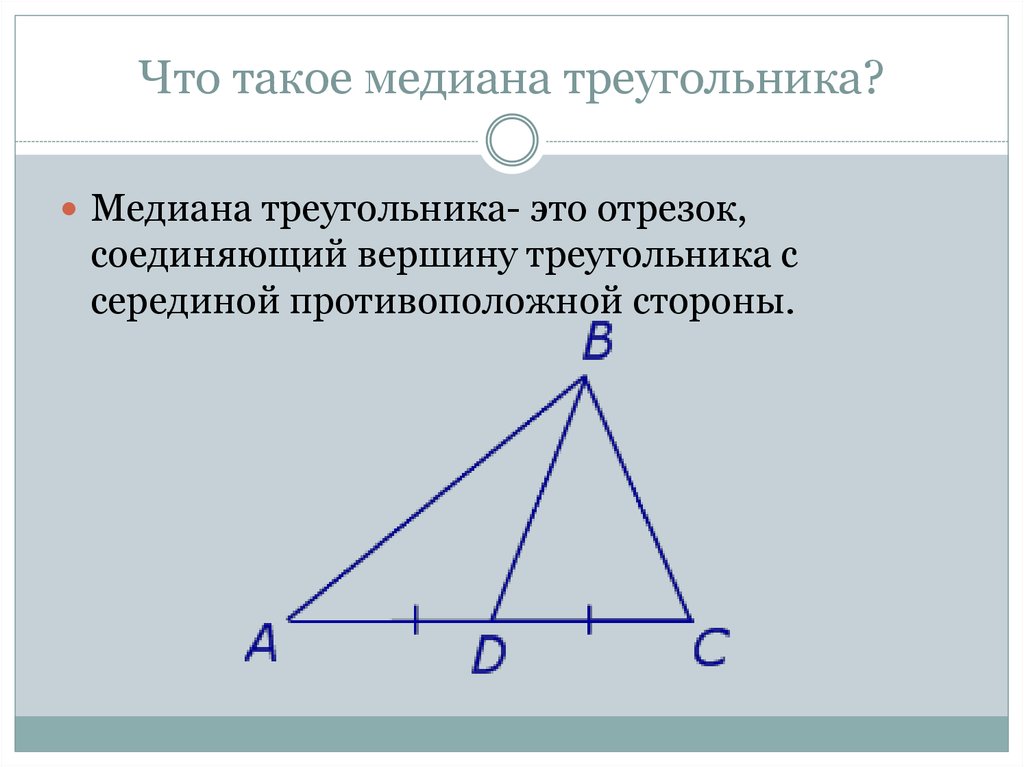
2. Что такое медиана треугольника?

Медиана треугольника- это отрезок,
соединяющий вершину треугольника с
серединой противоположной стороны.

3.

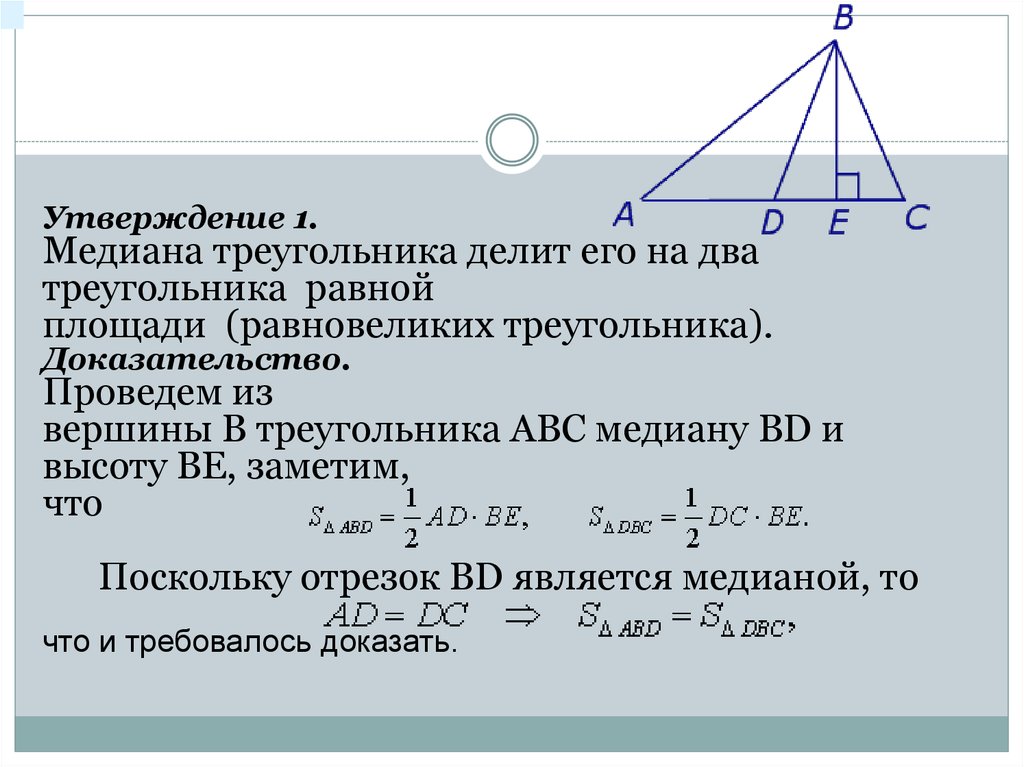
Утверждение 1.
Медиана треугольника делит его на два
треугольника равной
площади (равновеликих треугольника).
Доказательство.
Проведем из
вершины B треугольника ABC медиану BD и
высоту BE, заметим,
что
Поскольку отрезок BD является медианой, то
что и требовалось доказать.

4.

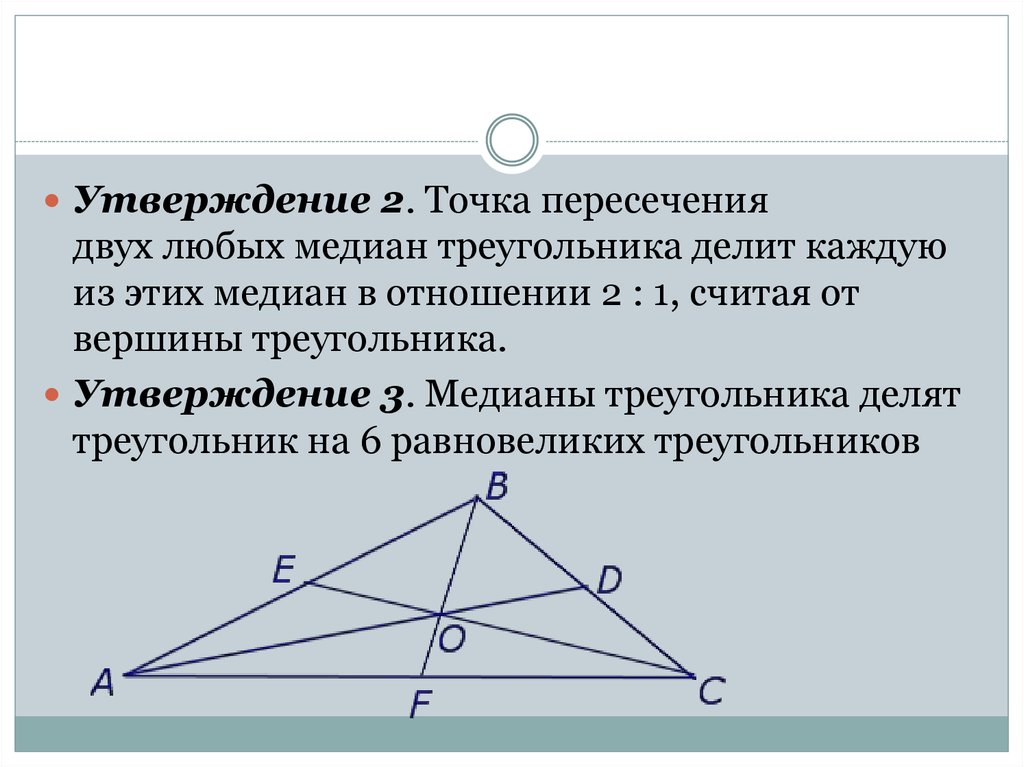
Утверждение 2. Точка пересечения
двух любых медиан треугольника делит каждую
из этих медиан в отношении 2 : 1, считая от
вершины треугольника.
Утверждение 3. Медианы треугольника делят
треугольник на 6 равновеликих треугольников

5.

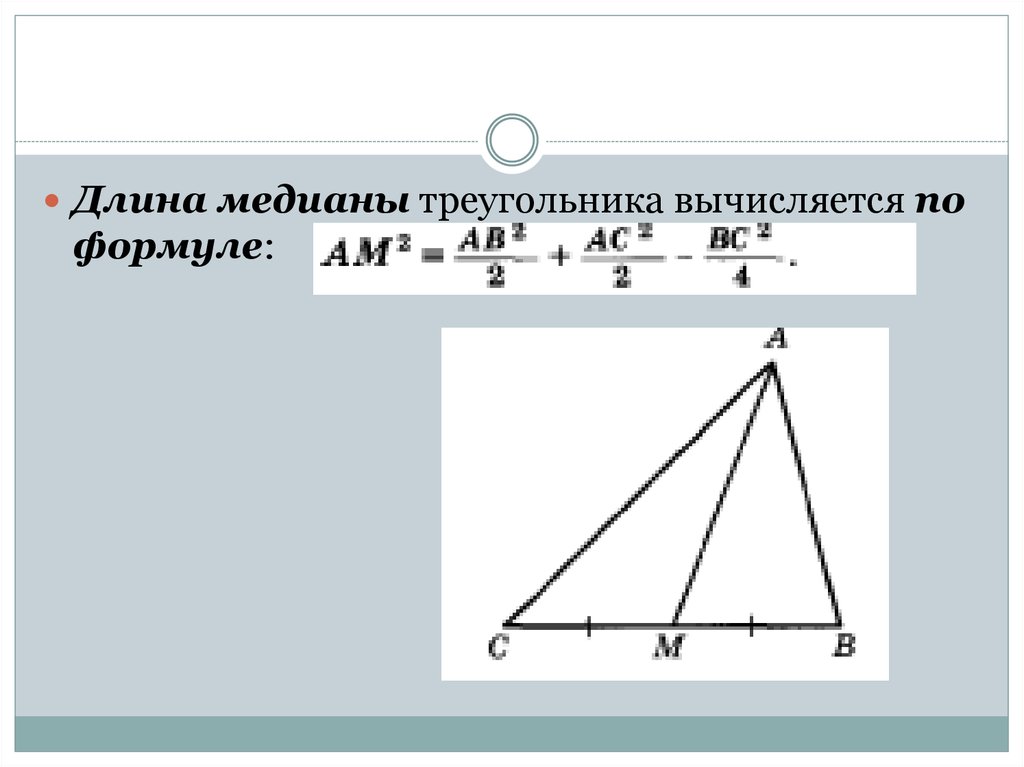
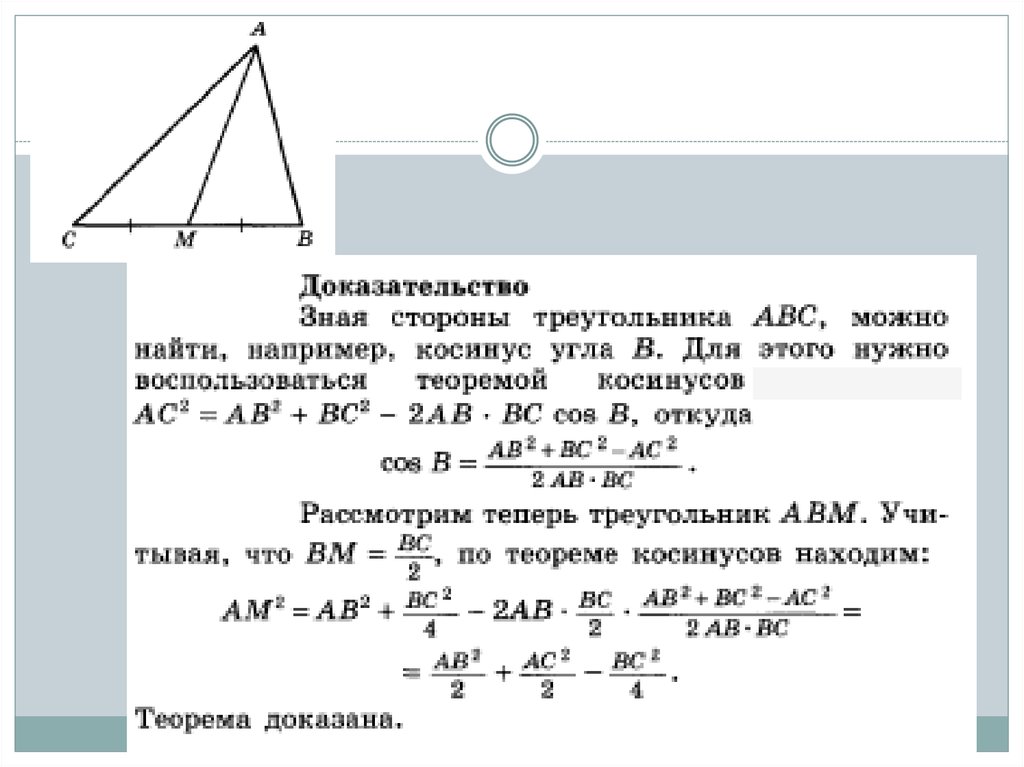
Длина медианы треугольника вычисляется по
формуле:

6.

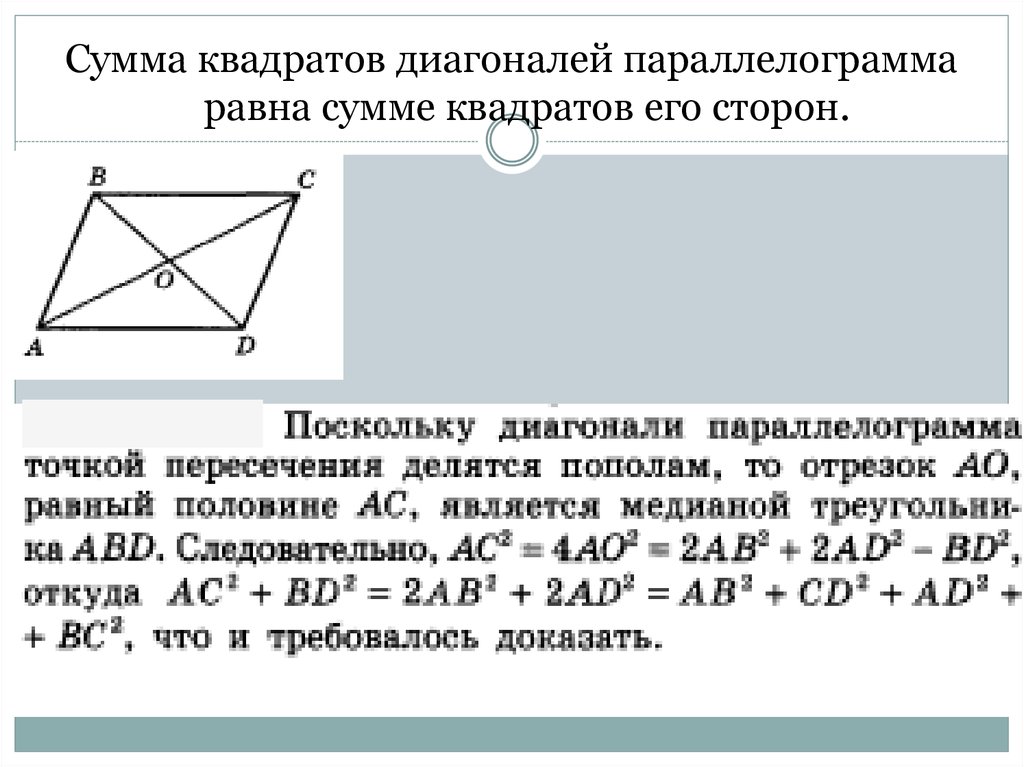
7. Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.

8.

Следствие. Длины медиан и длины сторон
треугольника связаны формулой

9.

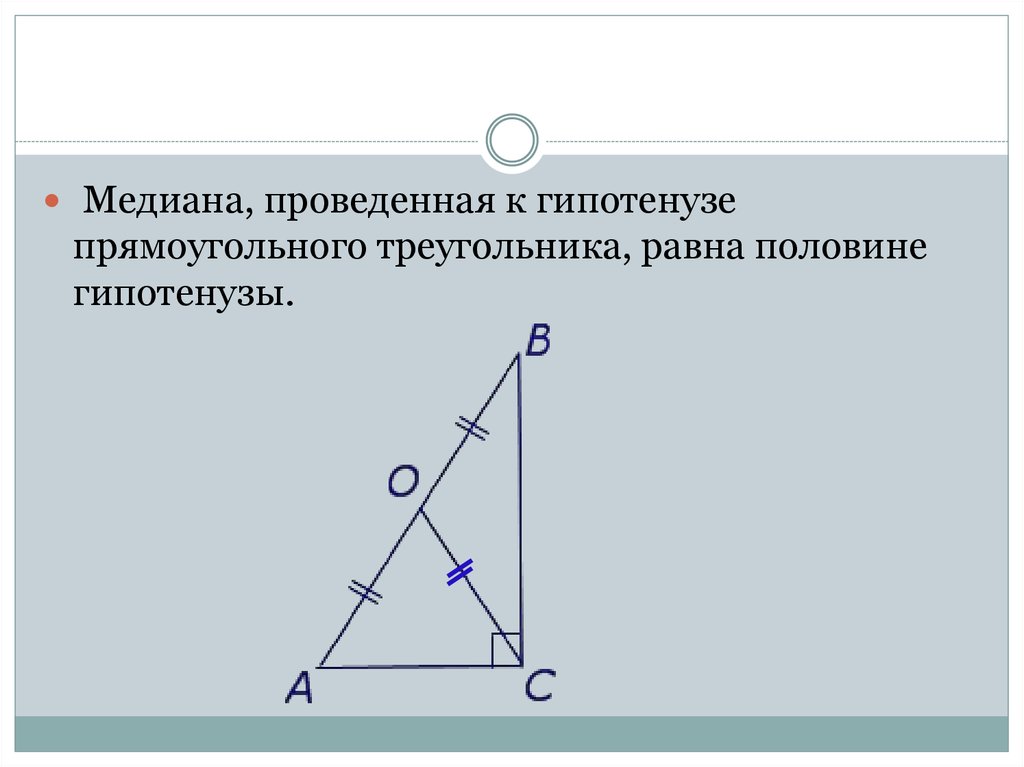
Медиана, проведенная к гипотенузе
прямоугольного треугольника, равна половине
гипотенузы.

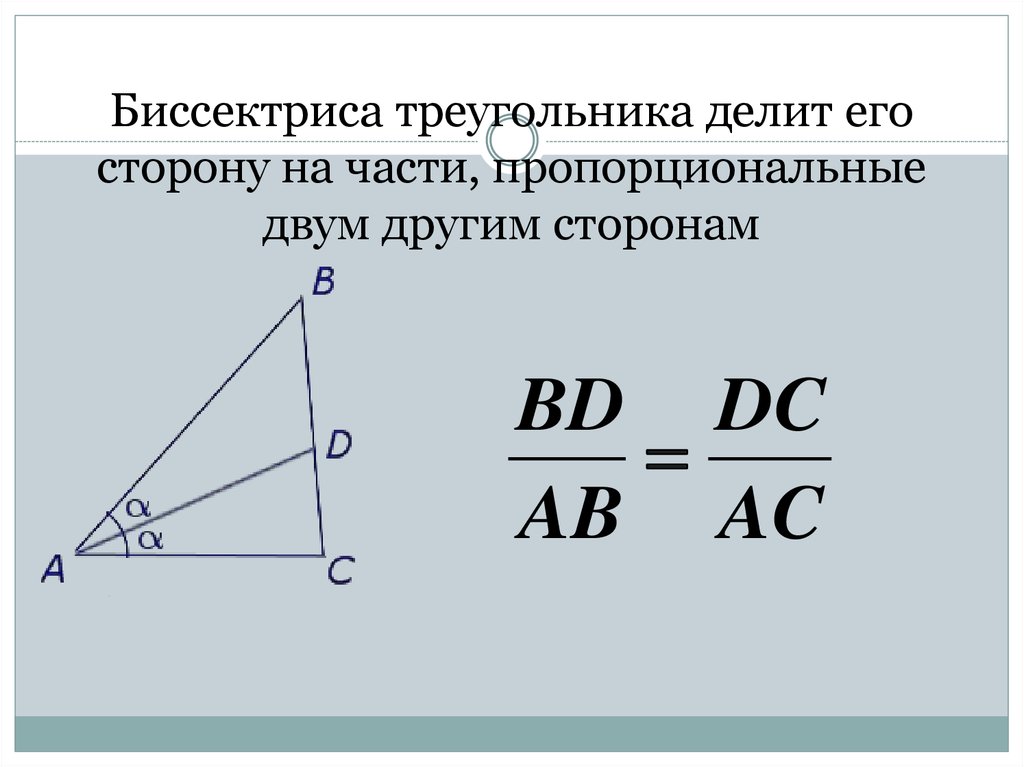
10. Биссектриса треугольника делит его сторону на части, пропорциональные двум другим сторонам

BD DC
AB AC

11.

Для длины
биссектрисы справедлива формула:
2bc
A
АD
cos
b c
2
AD bc a1a2

12.

Точка пересечения биссектрис О делит
биссектрису СD
СО a b
DO
c
(теорема Ван-Обеля)