Вычисление биссектрис и медиан треугольника

1.

09.02.2017

2.

Теорема о биссектрисе треугольника:
Биссектриса треугольника делит его сторону на
части, пропорциональные двум другим сторонам
А
1
В
ДС
ВД
=
АС
АВ
2
D
С
)

3.

Следствие:
В ΔАВС со сторонами АВ , ВС, АС и
биссектрисой AD справедливы равенства
А
1
В
BC AB
1) DB
,
AC AB
2
ВС AС
2) DС
,
AC AB
D
С

4.

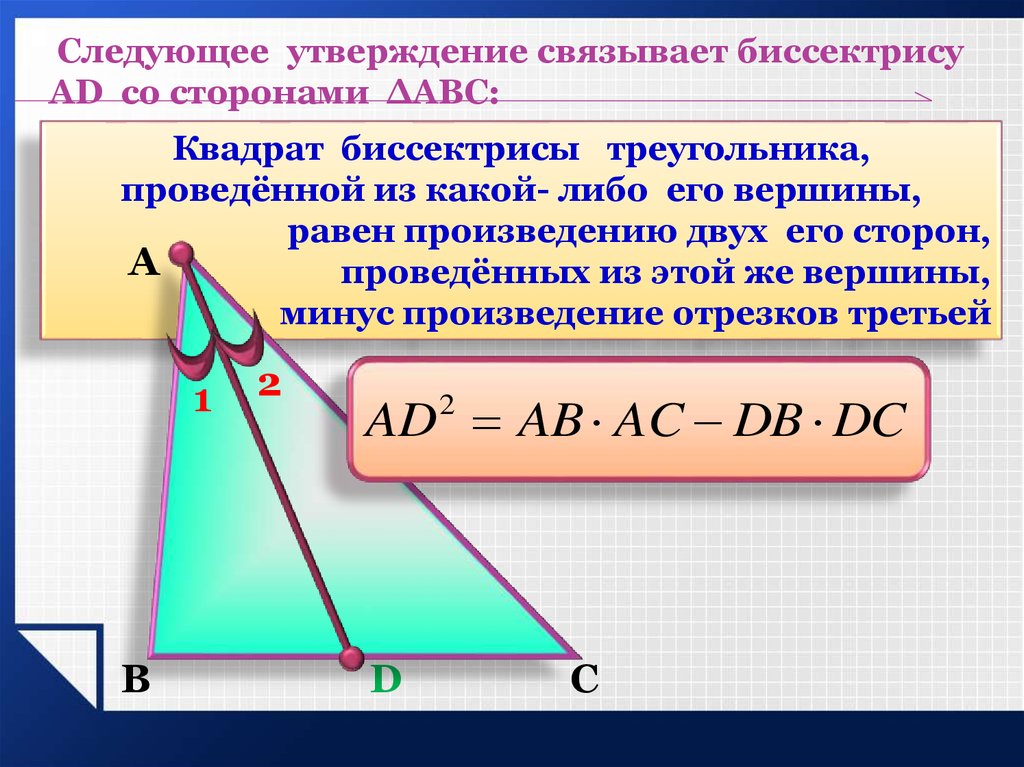
Следующее утверждение связывает биссектрису
AD со сторонами ΔАВС:
Квадрат биссектрисы треугольника,
проведённой из какой- либо его вершины,
равен произведению двух его сторон,
А
проведённых из этой же вершины,
минус произведение отрезков третьей
1
В
2
AD AB AC DB DC
2
D
С

5.

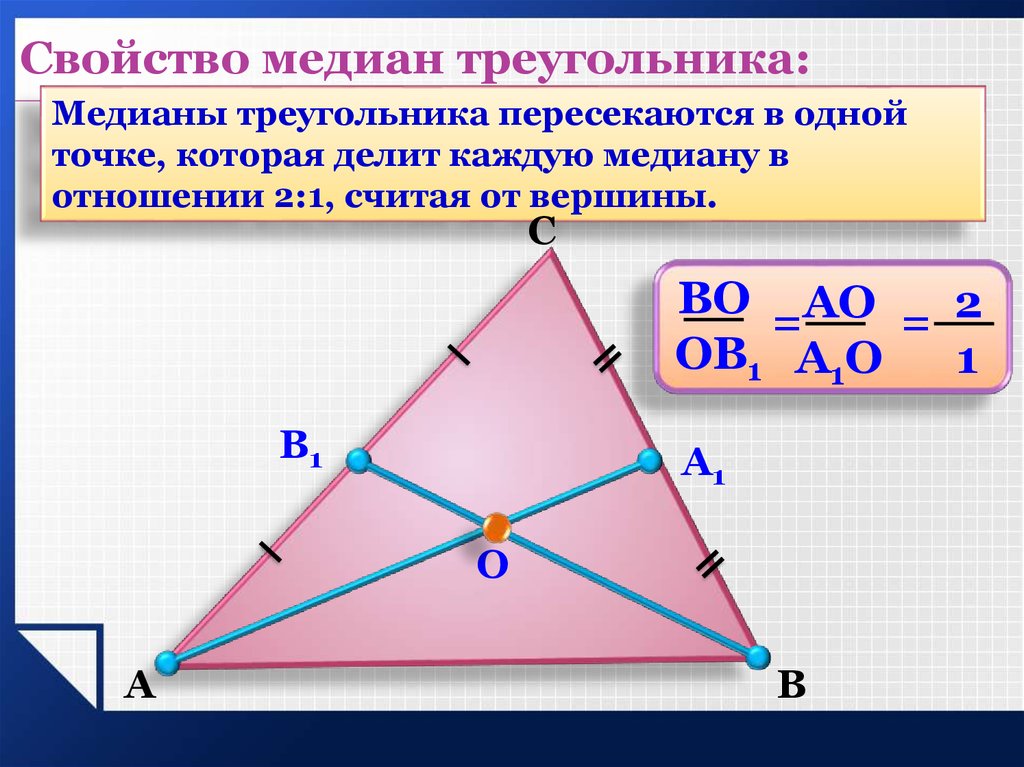
Свойство медиан треугольника:
Медианы треугольника пересекаются в одной
точке, которая делит каждую медиану в
отношении 2:1, считая от вершины.
С
ВО АО
2
=
=
ОВ1 А1О
1
В1
А1
О
А
В

6.

Дано: АВС, ВВ1 = 15 см
Найти: ВО, ОВ1
В1
Задача 1
С
5
А1
О
10
А
С1
В

7.

Дано: АВС, ОВ1 = 4 см
Найти: ВО, ВВ1
В1
Задача 2
С
4
А1
О
8
А
С1
В

8.

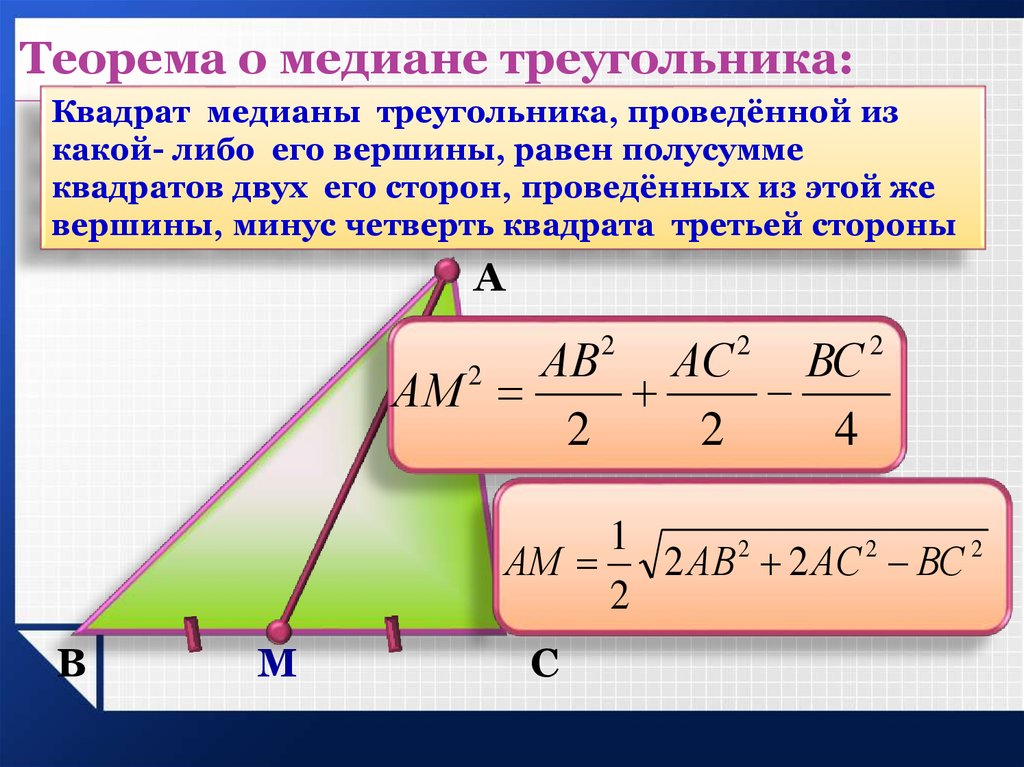
Теорема о медиане треугольника:
Квадрат медианы треугольника, проведённой из
какой- либо его вершины, равен полусумме
квадратов двух его сторон, проведённых из этой же
вершины, минус четверть квадрата третьей стороны
А
АВ АС ВС
АМ
2
2
4
2
2
2
2
1
2
2
2
АМ
2 АВ 2 АС ВС
2
В
М
С

9.

Следствие:
Сумма квадратов диагоналей параллелограмма
равна сумме квадратов его сторон.
D
С
АС2+ВД2=АВ2+ВС2+СД2+АД2
АС2+ВД2=2АВ2+2ВС2
А
В

10.

Задача 3
Основание треугольника равно 22 дм,
а боковые стороны 13 дм и 19 дм.
Определить медиану основания.
А
Ответ: 12 дм
В
М
С

11.

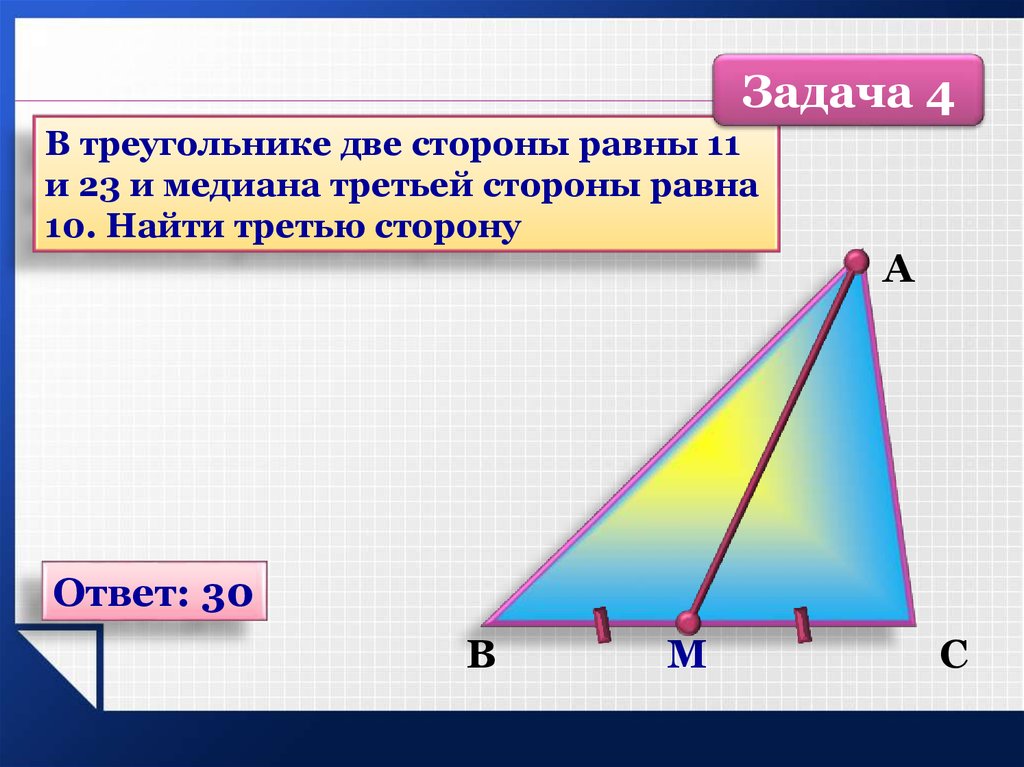
Задача 4
В треугольнике две стороны равны 11
и 23 и медиана третьей стороны равна
10. Найти третью сторону
А
Ответ: 30
В
М
С

12.

Задача 5
В треугольнике ABC определить
биссектрису А при следующей длине
сторон: 1) а = 7, b = 6, с = 8;
А
2) а = 18, b =15, с = 12;
1
2
Ответ: 1) 6
Ответ: 2) 10
В
D
С

13.

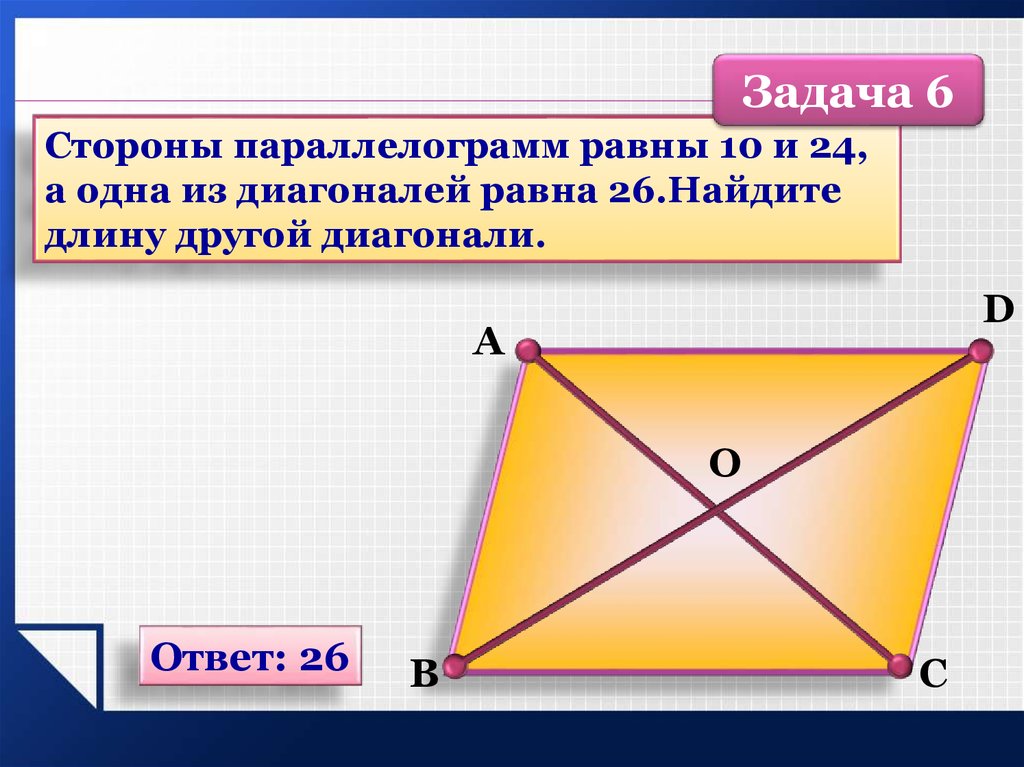
Задача 6
Стороны параллелограмм равны 10 и 24,
а одна из диагоналей равна 26.Найдите
длину другой диагонали.
D
А
О
Ответ: 26
В
С

14.

конспект
В треугольнике ABC определить биссектрису угла А
при следующей длине сторон: а = 39, b = 20, с = 45.
вопросы 17 – 22 (стр. 157)
Стороны треугольника равны 11, 13 и 12. Найдите
медиану, проведённую к большей стороне.
№32, №
3311(стр.
158)
Стороны параллелограмма
равны
и 23,
а диагонали
относятся как 2:3. Найти длины диагоналей
Повторить: формулы площадей