Метод излучательности (Radiosity)

1. Метод излучательности (Radiosity)

Будак Владимир Павлович,
НИУ «МЭИ»
кафедра светотехники
: +7 (495) 763-5239
[email protected]

2. Уравнение излучательности

(r)
2
M (r) M 0 (r)
M
(
r
)
F
(
r
,
r
)
(
r
,
r
)
d
r
ˆ
N
r
ˆ (r ),(r r ) N
ˆ (r ),(r r )
N
cos cos
F (r, r )
r r
k (r , r )
r 2
4
ˆl (r r )
r r
( r )
F (r , r ) (r , r )
M (r ) M 0 (r ) M (r )k (r , r )d r
2
ˆ
N
r
(r,r )=0
(r,r )=1
Уравнение излучательности является уравнением Фредгольма II рода.
Численный метод его решения основан на замене интеграла суммой.

3. Метод конечных элементов

Борис Григорьевич Галёркин (20.02.1871, Полоцк – 12.06.1945, Ленинград) –
советский механик и математик, академик АН СССР (1935; член-корр. 1928),
инженер-генерал-лейтенант
Иван Григорьевич Бубнов (6.01.1872, Нижний Новгород – 13.03.1919,
Петроград) — российский корабельный инженер, математик и механик
Вальтер Ритц (Walter Ritz, 22.02.1878, Сьон (Зиттен) – 7.06.1909, Гёттинген) –
швейцарский физик-теоретик и математик. Окончил Цюрихский университет (1900).
N
R (r ) M (r ) M 0 (r ) M (r )k (r , r )d 2 r 0
M (r ) M (r ) M j j (r )
j 1
i 1, N : ( R, i ) R(r ) i (r )d 2r 0
i ( M 0 , i ), ij ( i , j ),
N
M
j 1
N
j
( j , i ) ( M 0 , i ) M j ( k (r, r ) j (r )d 2 r , i ) 0
j 1
Aij ij i (r ) k (r, r ) j (r )d 2 r d 2 r :
AM
МКЭ (FEM) – дискретизация уравнения разложением по системе
базисных функций и сведения его к решению СЛАУ

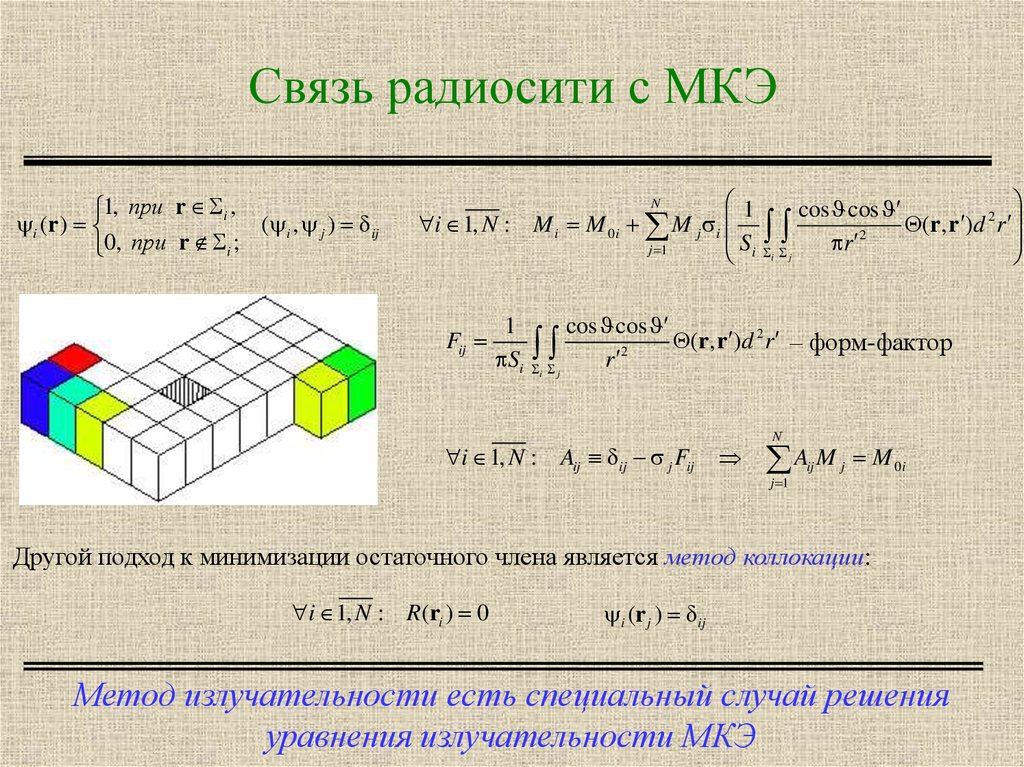
4. Связь радиосити с МКЭ

1, при r i ,
i (r )
( i , j ) ij
0, при r i ;
1
i 1, N : M i M 0i M j i
Si
j 1
N
Fij
1
S i
i j
i 1, N :
cos cos
2
r 2 (r, r )d r
i
j
cos cos
(r, r )d 2 r – форм-фактор
2
r
Aij ij j Fij
N
A M
j 1
ij
j
M 0i
Другой подход к минимизации остаточного члена является метод коллокации:
i 1, N : R (ri ) 0
i (r j ) ij
Метод излучательности есть специальный случай решения
уравнения излучательности МКЭ

5. Итерационные методы решения задачи излучательности

В задачах визуализации 3М сцен количество граней превышает десятки тысяч, что делает
обращение матрицы при решении СЛАУ математически некорректной задачей
N
N
N
N
j 1
j 1
j 1
j i
j 1
j i
Aii Fij i Fii j Fij i Fii j Fij Aij
N
Aij
j 1
j i
Aii
M i
Mj
M 0i
Aii
Находить решение простейшим методом итераций Якоби
(Jacobi) – соответствует кратностям переотражений:
M
i 1
Метод итераций Гаусса-Зейделя (Gauss-Seidel): M
(m)
i
j 1
Aij
Aii
(m)
i
M
N
Aij
j 1
j i
Aii
(m)
j
N
M (j m 1)
Aij
A
j i 1
ii
M 0i
Aii
M (j m 1)
M 0i
Aii
Сходимость метода можно ускорить, если выбирать последовательность
элементов очередного шага итерации не произвольно, а тех, вычисления
которых, в наибольшей степени уточняет решение.

6. Итерация Саусвелла (Southwell)

i=SiMi – полный поток лучистой энергии, уходящий с площадки i
i=SiM0i – поток лучистой энергии, излученный с площадки i
S
Kij i Aij ij i F ji : K
Sj
r
(k )
ε Kμ , ri
(k )
( k 1)
i
N
1
(k )
i Kij i
Kii
j i
N
(k )
i Kij (jk )
j 1
r ( k 1) ε Kμ ( k 1) r ( k ) Kμ ( k ) Kμ ( k 1) r ( k ) K μ ( k 1) μ ( k )
( k 1)
i
N
N
1
1
ri( k )
(k )
(k )
(k )
i( k )
i Kij i
i Kij i Kii i
Kii
j i
j 1
Kii
K ii
Поскольку на каждом шаге итераций изменяется только одно значение вектора (k), то
только один элемент вектора ( (k+1) (k)) отличен от нуля (допустим i):
rj( k 1) rj( k ) K ji ( i( k 1) i( k ) ) rj( k )
K ji
K ij
ri( k )
С физической точки зрения вектор ошибок представляет собой
неизлученную часть света с каждой грани

7. Общая схема метода излучательности

1.
2.
3.
4.
Представление сцены в виде сетки граней с заданными фотометрическими
характеристиками
Вычисление форм-факторов между всеми гранями сцены
Решение уравнения излучательности итерационным методом
Проецирование результатов на картинную плоскость с использованием
алгоритмов закрашивания
Решение после остановки на произвольном шаге итерации можно улучшить, если
распределить оставшуюся нераспределенной световую энергию, используя
представление о помещении как о фотометрическом шаре
N
E
M0
, ave
1 ave
A
i 1
N
i
i
A
i 1
i
N
H
r
i 1
(k )
i
N
1 ave Ai
i 1
Позволяет улучшить результат на каждом шаге итераций,
определяя всенаправленный (ambient) источник излучения

8. Адаптивные сети

Проблема визуализации методом излучательности – выбор размеров сетки
Время и точность решения накладывают противоречивые требования
Для равномерно освещенных поверхностей мелкая сетка не добавит точности
Сильно неравномерно освещенные грани (тень) нуждаются в мелком разбиении
Идеальным является крупное разбиение равномерно освещенных граней и мелкое в
местах сильной неравномерности
• Порочный круг: для хорошего решения задачи визуализации необходимо знать искомое
распределение освещенности по сцене
• Адаптивное разбиение - переразбиение поверхностей объекта при значительном
градиенте облученности вершин грани
A
K
E A EB
Eсреднее
C
Kпорог
D
B
Иной путь – решение в несколько проходов
оптимально в 3 прохода: грубый расчет, уточнение сетки, точно