Похожие презентации:
Первообразная и интеграл
1. Первообразная и интеграл
2.
Определение производной функции?Производной функции в данной точке называется
предел отношения приращения функции в этой точке к
приращению аргумента, когда приращение аргумента ,
стремиться к нулю.
3.
Устная работа1
сosх
sinх+12
4.
Устная работа-
5.
Используя определение производной функции,решают ряд задач в алгебре, физике, химии.
Рассмотрим физический смысл производной.
материальная
точка
s(t) закон
движения
6.
Задача:Точка движется прямолинейно по закону
s(t) = t3+ 2t ( где s(t) – измеряется в м).
Найдите скорость точки в момент времени t=2с.
Решение:
v(t) = 3t2 + 2
v(2) =
Ответ: 14 м/с.
7.
Задача: По прямой движется материальная точка,скорость которой в момент времени t задается
формулой v(t) = 3t2. Найдите закон движения.
Решение: Пусть s(t) – закон движения
надо найти функцию,
производная которой
равна 3t2 .
Эта задача решена верно, но не полно.
Эта задача имеет бесконечное множество решений.
3t2
3t2
3t2
3t2
можно сделать вывод, что
любая функция вида
s(t)=t3+C является
решением данной задачи,
где C любое число.
8.
При решении задачи, мы, зная производнуюфункции, восстановили ее первичный образ.
Эта операция восстановления - операция
интегрирования.
Востановленная функция – первообразная
( первичный образ функции)
Операция
дифференцирования
функция y = F(х)
(первообразная)
y = f(х)
производная
Операция
интегрирования
9. Первообразная
• Функция F(x) называется первообразнойдля функции f(x) на данном промежутке,
если для любого x из этого промежутка
F’(x) = f(x).
Пример:
Первообразной для функции f(x)=x на всей
числовой оси является F(x)=x2/2, поскольку
(x2/2)’=x.
10.
Операциядифференцирования
функция y = F(х)
(первообразная)
y = f(х)
производная
Операция
интегрирования
В математике много операций которые
являются обратными
32 = 9
?
?
Сегодня мы познакомились с новой операцией
интегрирование
? дифференцирование
11.
Запомните: Первообразная – это родительпроизводной:
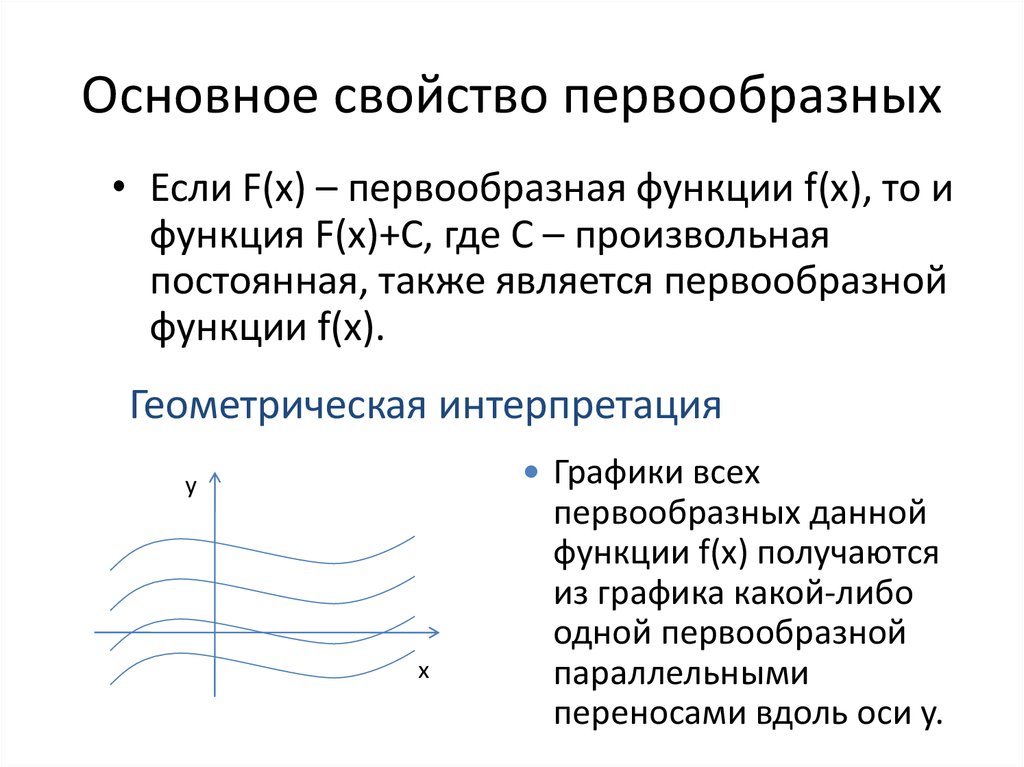
12. Основное свойство первообразных
• Если F(x) – первообразная функции f(x), то ифункция F(x)+C, где C – произвольная
постоянная, также является первообразной
функции f(x).
Геометрическая интерпретация
Графики всех
y
x
первообразных данной
функции f(x) получаются
из графика какой-либо
одной первообразной
параллельными
переносами вдоль оси y.
13.
f(x)1
F(x)
Задача:
Найдите все первообразные
для функций:
f(х)=3
f(х)= х2
f(х)=cosx
f(х)=12
f(х)=х5
14.
Три правила нахождения первообразныхЕсли функции у=f(x) и у=g(x) имеют на
промежутке
первообразные соответственно у=F(x) и у=G(x), то
Функция
Первообразная
у = f(x) + g(x)
у = F(x) + G(x)
у =k f(x)
у =k F(x)
15.
16.
СамостоятельноДля функции y=f(x) найдите хотя бы одну первообразную:
17. Неопределенный интеграл
• Совокупность всех первообразных даннойфункции f(x) называется ее неопределенным
интегралом и обозначается f ( x)dx :
f ( x)dx F ( x) C
,
где C – произвольная постоянная.
18. Правила интегрирования
cf ( x)dx c f ( x)dx, c const( f ( x) g ( x))dx f ( x)dx g ( x)dx
1
f (ax b)dx F (ax b) C , a 0
a
19. Определенный интеграл
• В декартовой прямоугольнойсистеме координат XOY фигура,
ограниченная осью OX, прямыми
x=a, x=b (a<b) и графиком
непрерывной неотрицательной
на отрезке [a;b] функции y=f(x),
называется криволинейной
трапецией
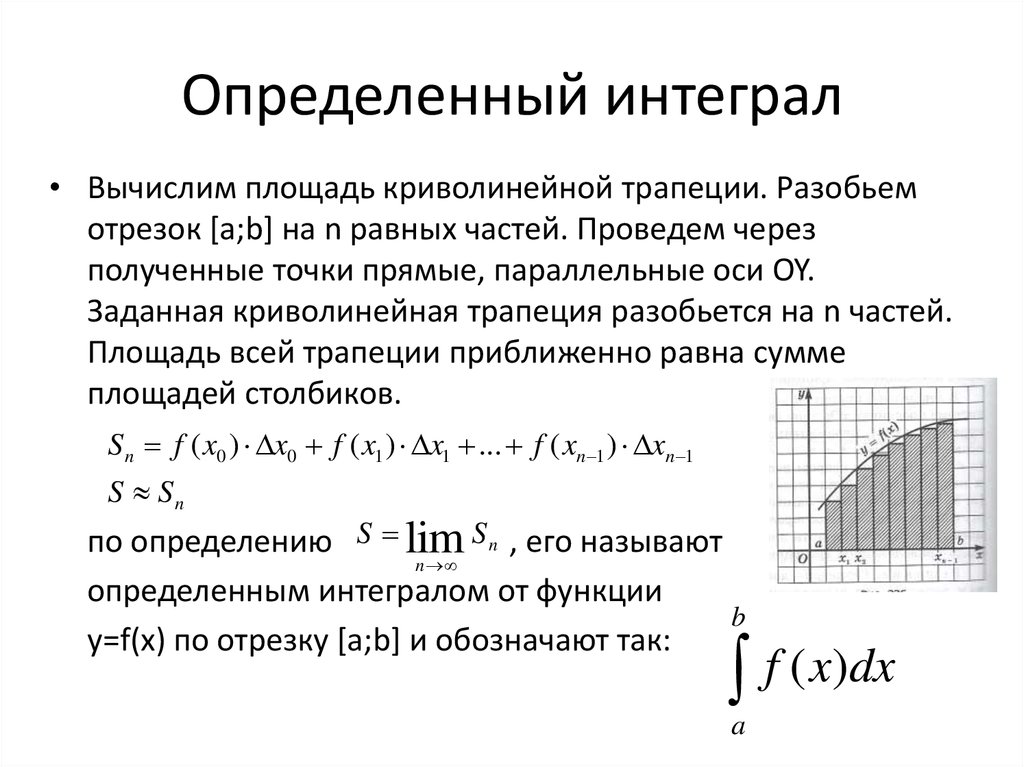
20. Определенный интеграл
• Вычислим площадь криволинейной трапеции. Разобьемотрезок [a;b] на n равных частей. Проведем через
полученные точки прямые, параллельные оси OY.
Заданная криволинейная трапеция разобьется на n частей.
Площадь всей трапеции приближенно равна сумме
площадей столбиков.
S n f ( x0 ) x0 f ( x1 ) x1 ... f ( xn 1 ) xn 1
S Sn
по определению S lim S n , его называют
n
определенным интегралом от функции
b
y=f(x) по отрезку [a;b] и обозначают так:
f ( x)dx
a
21. Связь между определенным интегралом и первообразной (Формула Ньютона - Лейбница)
• Для непрерывной функцииb
f ( x)dx F ( x) | F (b) F (a)
b
a
a
где F(x) – первообразная функции f(x).
22. Основные свойства определенного интеграла
af ( x)dx 0
a
b
dx b a
a
b
a
a
f ( x)dx f ( x)dx
b
23. Основные свойства определенного интеграла
ba
c
b
a
c
f ( x)dx f ( x)dx f ( x)dx
b
b
a
a
cf ( x)dx c f ( x)dx, c const
b
b
b
a
a
a
(
f
(
x
)
g
(
x
))
dx
f
(
x
)
dx
g
(
x
)
dx
24. Геометрический смысл определенного интеграла
• Площадь криволинейной трапеции,ограниченной графиком непрерывной
положительной на промежутке [a;b]
функции f(x), осью x и прямыми x=a и x=b:
b
S f ( x)dx
a
25. Геометрический смысл определенного интеграла
• Площадь криволинейной трапеции,ограниченной графиком непрерывной
отрицательной на промежутке [a;b]
функции f(x), осью x и прямыми x=a и x=b:
b
S f ( x)dx
a
26. Геометрический смысл определенного интеграла
• Замечание: Если функция изменяет знак напромежутке [a;b]
,
то
b
S1 S 2 f ( x)dx
a
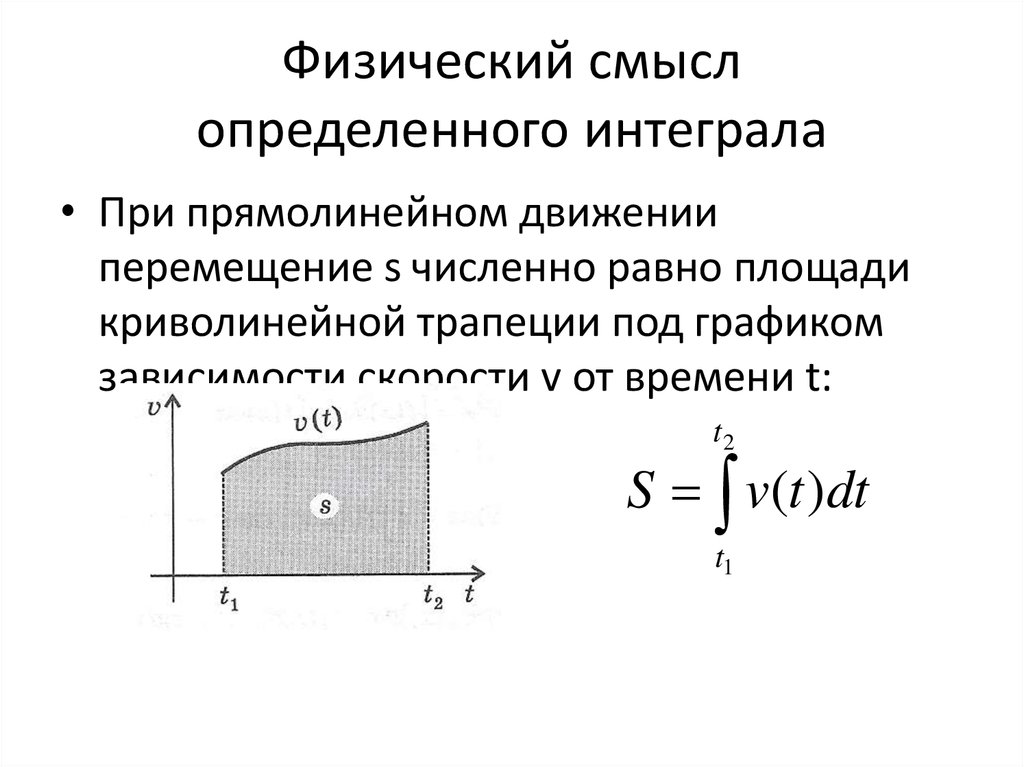
27. Физический смысл определенного интеграла
• При прямолинейном движенииперемещение s численно равно площади
криволинейной трапеции под графиком
зависимости скорости v от времени t:
t2
S v(t )dt
t1
28. Вычисление площадей и объемов
с помощью определенногоинтеграла
29. Площадь фигуры,
• Ограниченной графиками непрерывныхf ( x) g ( x)
функций y=f(x) и y=g(x) таких, что
для любого x из [a;b], где a и b – абсциссы
точек пересечения графиков функций:
b
S ( f ( x) g ( x)) dx
a
30. Объем тела,
• полученного в результате вращения вокругоси x криволинейной трапеции,
ограниченной графиком непрерывной и
неотрицательной функции y=f(x) на отрезке
[a;b]:
b
V f ( x)dx
2
a



























 Математика
Математика








