Теорема Муавра-Лапласа

1. ТЕОРЕМА МУАВРА-ЛАПЛАСА

ТЕОРЕМА МУАВРАЛАПЛАСА
Локальная и интегральная

2.

Пьер-Симо́н Лаплас (1749- 1827) - выдающийся
французский математик, физик и астроном; один
из создателей теории вероятностей. Был членом
Французского Географического общества.
Абрахам де Муавр (1667- 1754) — английский
математик французского происхождения. Член
Лондонского королевского общества (1697),
Парижской (1754) и Берлинской (1735) академий
наук.

3.

Теорема Муавра - Лапласа - простейшая из
предельных теорем теории вероятностей.
В общем виде теорема доказана Лапласом в книге
«Аналитическая теория вероятностей» (1812).
Один частный случай теоремы был известен
Муавру (1730), в связи с чем она и называется
теоремой Муавра-Лапласа.
Утверждает, что число успехов при многократном
повторении одного и того же случайного
эксперимента с двумя возможными исходами
приблизительно имеет нормальное распределение.

4.

Рассмотрим последовательность из n независимых
опытов, в каждом из которых событие A может
произойти с вероятностью p, либо не произойти с вероятностью q = 1 − p. Обозначим через Pn(m)
вероятность того, что событие A произойдет ровно
m раз из n возможных. Если n будет достаточно
большим, то найти значение Pn(m) по теореме
Бернулли становится нереально из-за огромного
объема вычислений. Локальная теорема Муавра Лапласа позволяет найти приближенное значение
вероятности.

5.

Локальная теорема Муавра - Лапласа. Если
в схеме Бернулли число n велико, а число p
отлично от 0 и 1, тогда:
Pn ( m)
m np
1
, где ( x)
npq
npq
1
e
2
x2
2
Функция φ(x) называется функцией Гаусса.
Теорема Муавра-Лапласа утверждает, что
асимптотическим выражением для биномиального
распределения является нормальная функция.

6.

Для расчетов составлена таблица значений функции φ
(x), необходимо учитывать свойства:
1. φ(−x) = φ(x) - четная, в таблице приведены значения
функции лишь для положительных аргументов;
2. Функция φ(x) - монотонно убывающая. Предел φ(x)
при x→∞ равен нулю.
3. Если х > 5, то можно считать, что φ(х) ≈ 0. Функция
φ(х) уже при х = 5 очень мала: φ(5)=0,0000015.
Поэтому таблица значений не продолжена для х > 5.

7.

Пример. Вероятность покупки при посещении
клиентом магазина составляет р = 0,75. Найти
вероятность, что при 100 посещениях клиент
совершит покупку ровно 80 раз.
Решение. n = 100, m = 80, p = 0,75, q = 0,25.
80 100 0, 75
x
1,16
Находим
,
100 0, 75 0, 25
определяем (1,16) = 0,2036, тогда:
Р100(80) =
0, 2036
0, 047
100 0, 75 0, 25

8.

Задание. Вероятность выпуска бракованного
изделия равна 0,02. Какова вероятность того, что
среди 2500 выпущенных изделий окажется 50
бракованных
Варианты ответов:
1) 0,1045;
2) 0,86; 3) 0,0570;
4) 0,0172;
5) 0,3989.
Ответ: пункт 5

9.

Фрагмент таблицы функции (x)
x
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
0
0,242
2179
1942
1714
1497
1295
1109
0940
0790
0656
1
2396
2155
1919
1691
1476
1276
1092
0925
0775
0644
2
2371
2131
1895
1669
1456
1257
1074
0909
0761
0632
3
2347
2107
1872
1647
1435
1238
1057
0893
0748
0620
4
2323
2083
1849
1626
1415
1219
1040
0878
0734
0608
5
2299
2059
1826
1604
1394
1200
1023
0863
0721
0596
6
2275
2036
1804
1582
1374
1182
1006
0848
0707
0584
1
2
7
2251
2012
1781
1561
1354
1163
0989
0833
0694
0573
2
x
e 2
8
2227
1989
1758
1539
1334
1145
0973
0818
0681
0562
9
2203
1965
1736
1518
1315
1127
0957
0804
0669
0551

10.

Интегральная теорема Муавра – Лапласа. Если
вероятность р наступления события А в каждом
испытании постоянна и отлична от 0 и 1, то
вероятность, что в n независимых испытаниях
(n>>1) событие А состоится число раз,
заключенное в границах от а до b включительно:
Pn (a m b) Ф( x2 ) Ф( x1 )
a np
b np
x1
, x2
.
npq
npq

11.

где функция Ф (х) определяется равенством
Ф( x)
1
2
x
e
t2
2
dt
0
Формула называется интегральной формулой
Муавра— Лапласа.
Получаемые по интегральной и локальной
формулам Муавра — Лапласа вероятности
достаточно точны, если произведение nр
составляет несколько сотен!!!

12.

Свойства функции Ф(х)
Функция Ф(х) нечетная, Ф (- х) = - Ф(х).
Функция Ф(х) монотонно возрастающая.
Предел функции Ф(х) при x→∞ равен 0,5.
Для всех значений х > 5 считают, что Ф (х) ≈ 0,5.
Уже Ф (5) = 0,4999992, при увеличении х
функция Ф (х) возрастает, но не может превосходить 0,5. Поэтому в таблицах функция дана
для значений х < 5.

13.

Оценка отклонения относительной частоты от
постоянной вероятности
Вероятность, что в n независимых испытаниях, в
каждом из которых вероятность появления
события А постоянна и равна р, абсолютная
величина отклонения относительной частоты
появления события А от его постоянной
вероятности не превысит положительного числа ,
приближенно равна:
m
P
p 2Ф
n
n
pq
.

14.

Пример. Вероятность появления события в
каждом из 625 независимых испытаний равна 0,8.
Найти вероятность, что относительная частота
появления события отклонится от его вероятности
по абсолютной величине не более, чем на 0,04.
Решение. По условию задачи: n = 625; p = 0,8;
=0,04. Отсюда q =1– p = 0,2. Требуется найти
вероятность:
m
Р
- 0,8 0, 04 = ?
625

15.

Для решения задачи воспользуемся формулой,
определяющей оценку отклонения относительной
частоты от постоянной вероятности:
m
P
p 2Ф
n
n
pq
.
Ф(х) – интегральная функция Лапласа. Найдем
аргумент функции Лапласа:
n
625
x
0, 04
2,5
pq
0,8 0,2
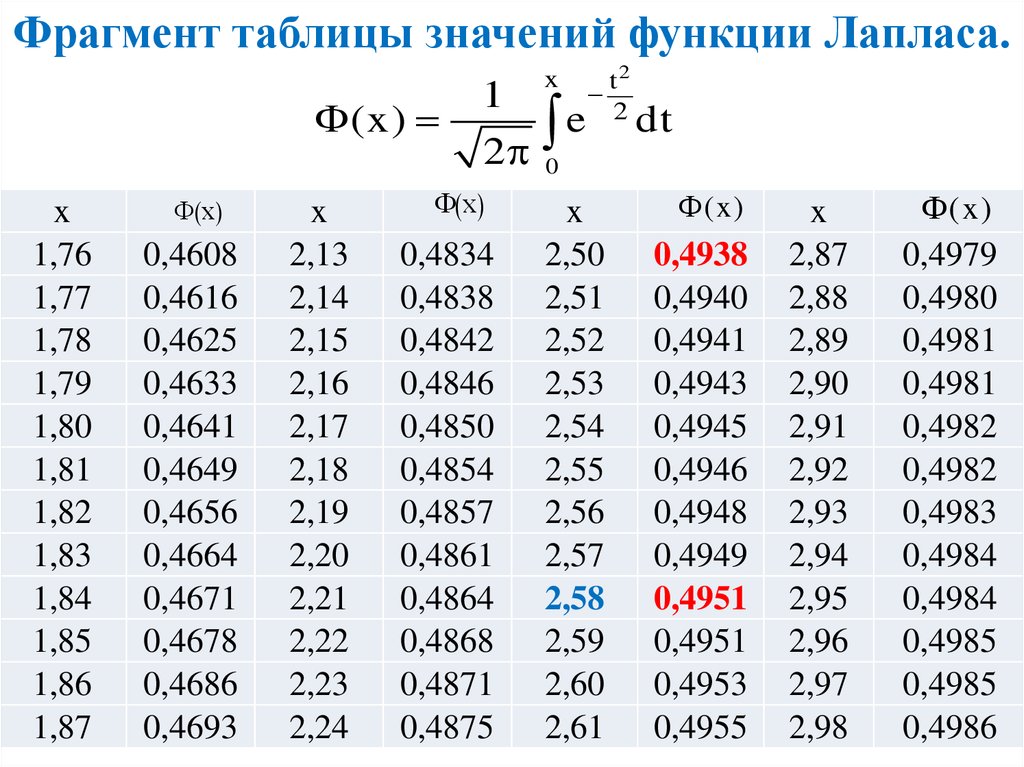
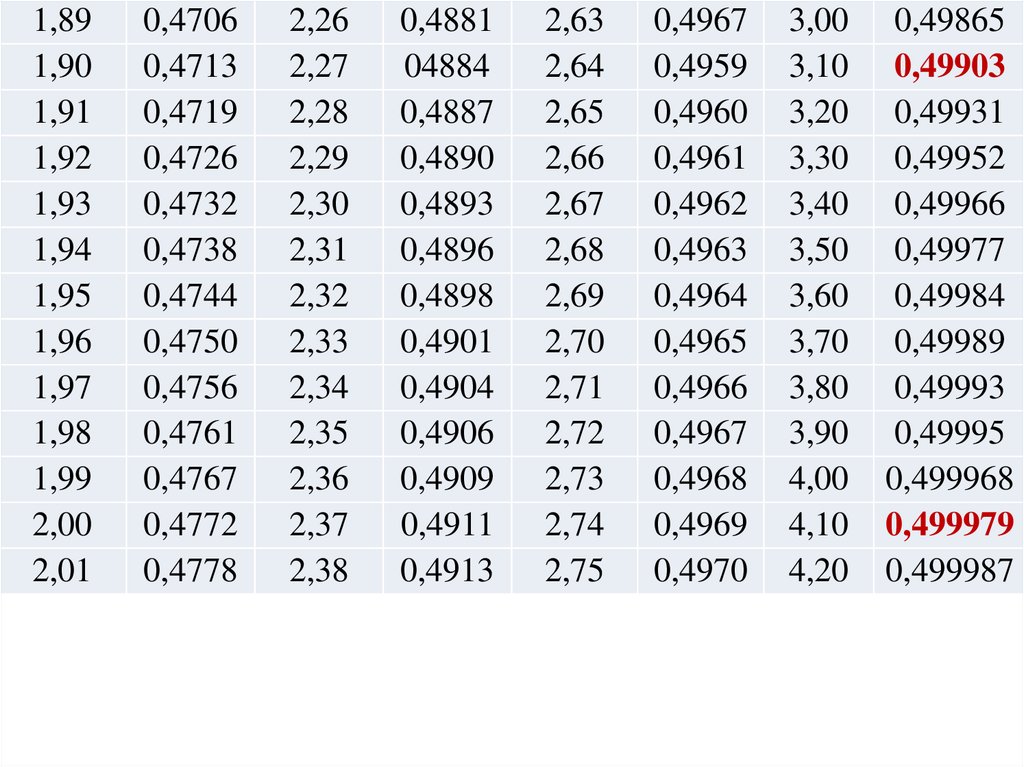
По табл. функции Лапласа: Ф(2,5) = 0,4938, т.е.
2Ф(х) = 0,9876.

16.

Итак, искомая вероятность:
m
Р
- 0,8 0,04 0,9876.
625

17.

Пример. При установившемся технологическом
режиме завод выпускает в среднем 70% продукции
1-го сорта. Определить вероятность, что из 1000
изделий число первосортных заключено между 652
и 760.
Решение. p = 0,7; q = 1 – p = 0,3; n = 1000;
np = 0,7 × 1000 = 700; npq = 700 × 0,3 = 210