Кривые второго порядка. Лекция №5

1. Лекция 5 Кривые второго порядка

2.

Общее уравнение кривой второго порядка
Окружность
Эллипс
Гипербола
Парабола

3. Общее уравнение кривой второго порядка

К кривым второго порядка относятся: эллипс, частным случаем
которого является окружность, гипербола и парабола.
Они задаются уравнением второй степени относительно x и y:
Ax 2 2Bxy Cy 2 2Dx 2Ey F 0
Общее уравнение кривой
второго порядка
В некоторых частных случаях это уравнение может определять
также две прямые, точку или мнимое геометрическое место.

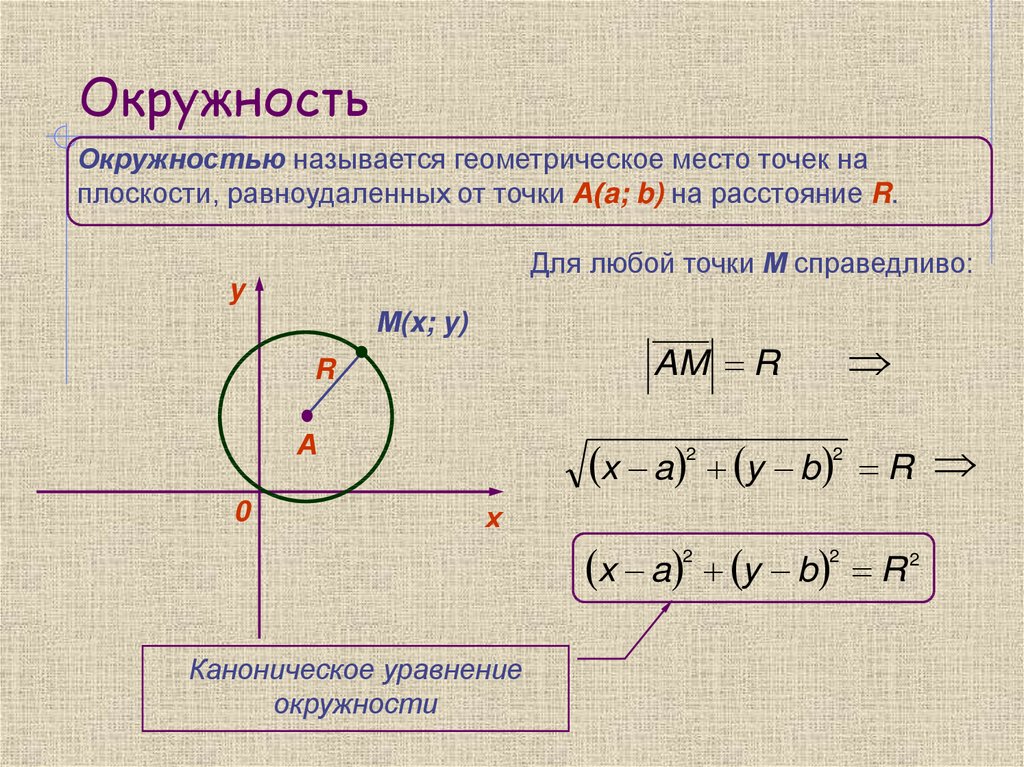
4. Окружность

Окружностью называется геометрическое место точек на
плоскости, равноудаленных от точки А(a; b) на расстояние R.
Для любой точки М справедливо:
y
М(x; y)
А
0
AM R
R
2
x a y b
R
2
x a y b
R2
2
х
2
Каноническое уравнение
окружности

5. Эллипс

Эллипсом называется геометрическое место точек, сумма
расстояний от каждой из которых до двух точек той же плоскости
F1 и F2, называемых фокусами, есть величина постоянная,
равная 2а.
Зададим систему координат и начало координат выберем в
середине отрезка [F1 F2]
r1 r2 2a
y
F1( c; 0);
M(x; y)
r2
r1
r1 F1M
x c
r2 F2M
x c
2
y2
F
F1
-c
F2 (c; 0)
0
c2
х
2
y2

6. Эллипс

x c
2
x c
y2
y 2 2a
2
x c y 2a 2 a x xc c y y
2
2
x c
2
4a
y 4a 4a
2
x c
2
2
x c
2
2
2
y
2
x c
2
22
2
:4
a cb x a y a (ba : (ca22)b2 )
22
2
2
2
x2 y 2
2 1
2
a
b
2
22
a 2 x 2 2a 2 xc a 2c 2 a 2 y 2 a 4 2a 2 xc x 2c 2
2
y2
y 2 4a 2 x 2 2 xc c 2 x 2 2 xc c 2
4a
a xx
cc
yy 4 aa22 4xc
xc 2
22
2
2
2
2
b2
Каноническое уравнение
эллипса

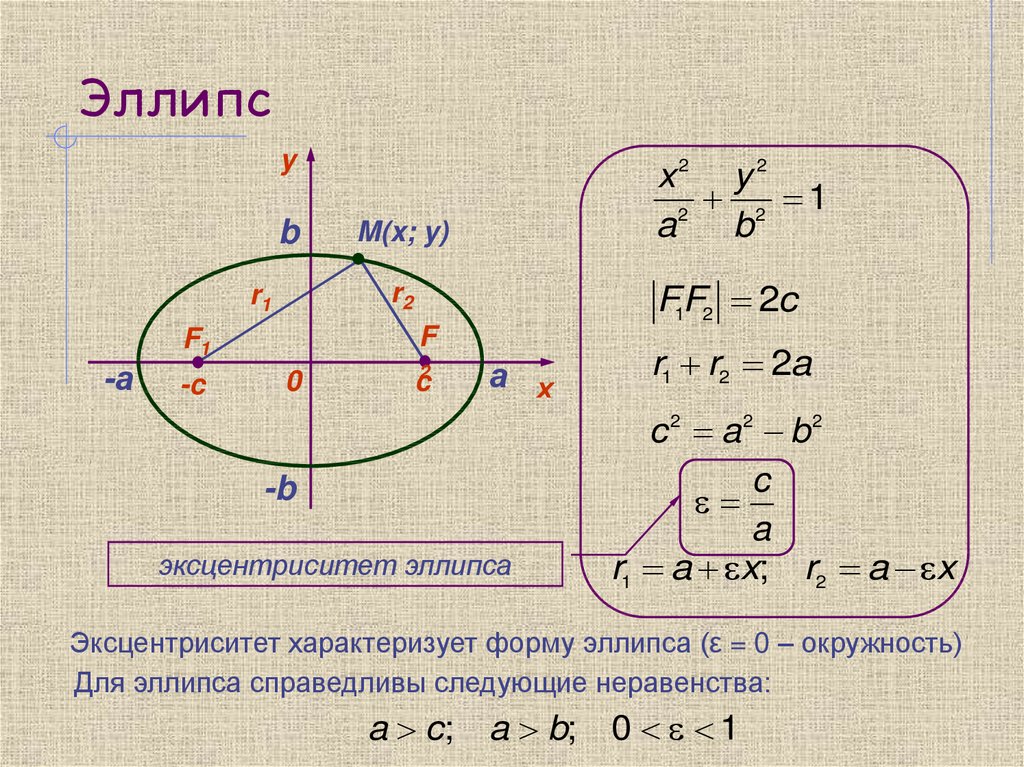
7. Эллипс

y
b
F1F2 2c
F
F1
-c
M(x; y)
r2
r1
-а
x2 y 2
2 1
2
a
b
0
c2
а х
-b
эксцентриситет эллипса
r1 r2 2a
c 2 a2 b2
c
a
r1 a x; r2 a x
Эксцентриситет характеризует форму эллипса (ε = 0 – окружность)
Для эллипса справедливы следующие неравенства:
a c;
a b;
0 1

8. Разновидности эллипса

Уравнение эллипса со смещенным центром
Y
( x x0 ) 2 ( y y0 ) 2
1
2
2
a
b
O ' ( x0 ; y 0 ) - центр эллипса
b
a
x0
X
y0
a
O'
b
Если в уравнении эллипса b a , то большой осью будет ось
B1 B2 2b , фокусы эллипса будут
B1 b
.
лежать на этой оси и связь
между параметрами эллипса
будет такой:
b2 a 2 c2
F1 c
a
O
.
F2 c
B2 b
a

9. Пример

Составить уравнение эллипса, фокусы которого лежат в
точках F1(-4; 0) F2(4; 0), а эксцентриситет равен 0,8.
c 4
c
0 .8
a
c 2 a2 b2
b 2 a 2 c 2 25 16 9
Каноническое уравнение эллипса:
y
3
-5
0
-3
c
4
a
5
0 .8
5 х
x2 y 2
1
25 9
b 3

10. Гипербола

Гиперболой называется геометрическое место точек, разность
расстояний от каждой из которых до двух точек той же плоскости
F1 и F2, называемых фокусами, есть величина постоянная,
равная 2а.
y
r1 r2 2a
M(x; y)
F1( c; 0);
r1
F
F1
-c
0
2
c
r2
х
F2 (c; 0)
r1 F1M
x c
r2 F2M
x c
2
2
y2
y2

11. Гипербола

x c
2
y2
x c
2
y 2 2a
x c
2
y2
x c
2
y 2 2a
После тождественных преобразований уравнение примет вид:
c ab2 2 x 2 a2 y 2 a2 (bc22 : (aa22)b2 )
2
x2 y 2
2 1
2
a
b
b2
Каноническое уравнение
гиперболы

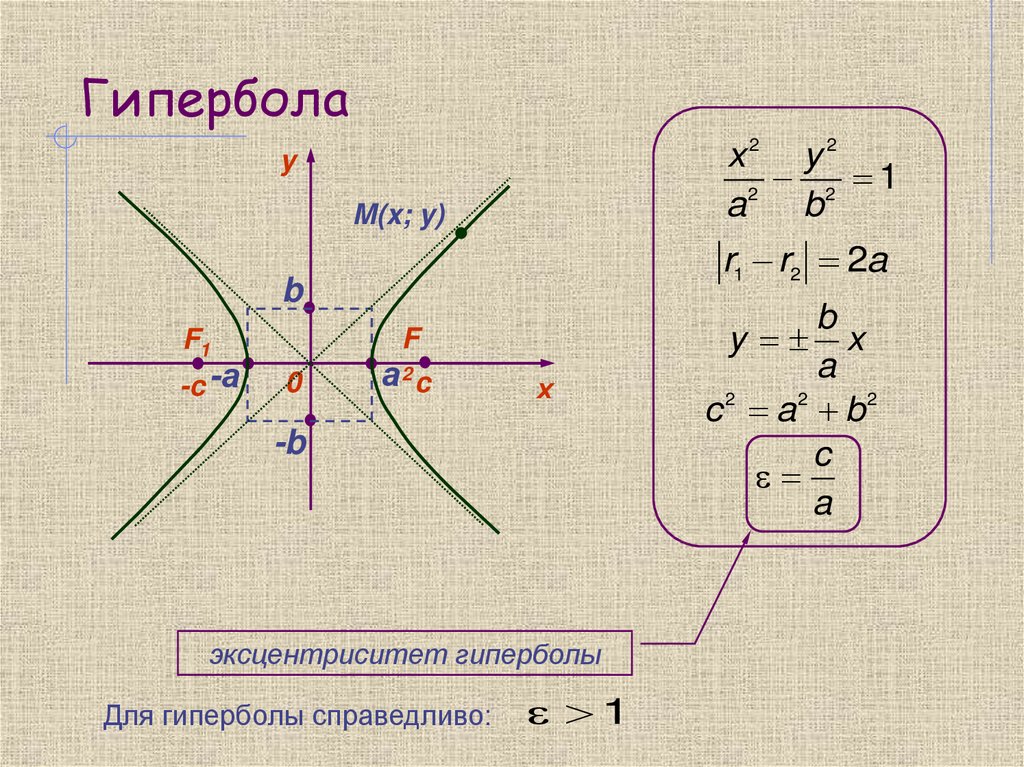
12. Гипербола

x2 y 2
2 1
2
a
b
y
M(x; y)
r1 r2 2a
b
F
F1
-c -а
0
а2 c
х
-b
эксцентриситет гиперболы
Для гиперболы справедливо:
1
b
y x
a
c 2 a2 b2
c
a

13. Построение гиперболы

x2 y2
2 1
2
a b
Построение гиперболы
Для построения гиперболы удобно пользоваться
вспомогательными построениями.
1. В системе координат строим прямоугольник с размерами 2a 2b
на осях OX и OY соответственно.
2. Проводим диагонали этого прямоугольника.
Уравнения диагоналей – это уравнения асимптот гиперболы
b
y x
a
3. На действительной оси отмечаем вершины гиперболы и от них
ведем ветви гиперболы к асимптотам.
Y
Y
Y
b
a
a
b
b
b
X
a
a
b
X
c a
a c
b
X

14. Пример

Составить уравнение гиперболы, проходящей через точку
А(6; -4), если ее асимптоты заданы уравнениями:
6
y
x
3
b
6
a
3
3b 6a
x2 y 2
62 ( 4)2
2 1 2 2 1
Точка А лежит на гиперболе
2
a
b
a
b
36b 2 16a 2 a 2b 2
2
3b 6a
b2 a2
Решим систему:
3
2
2
2 2
2
2
2 2
36b 16a a b
36
b
16
a
a
b
2 2
2
2
b
a
a 2 3
a
12
3
2
2
b 8
b 2 2
24a 2 16a 2 a 4
3

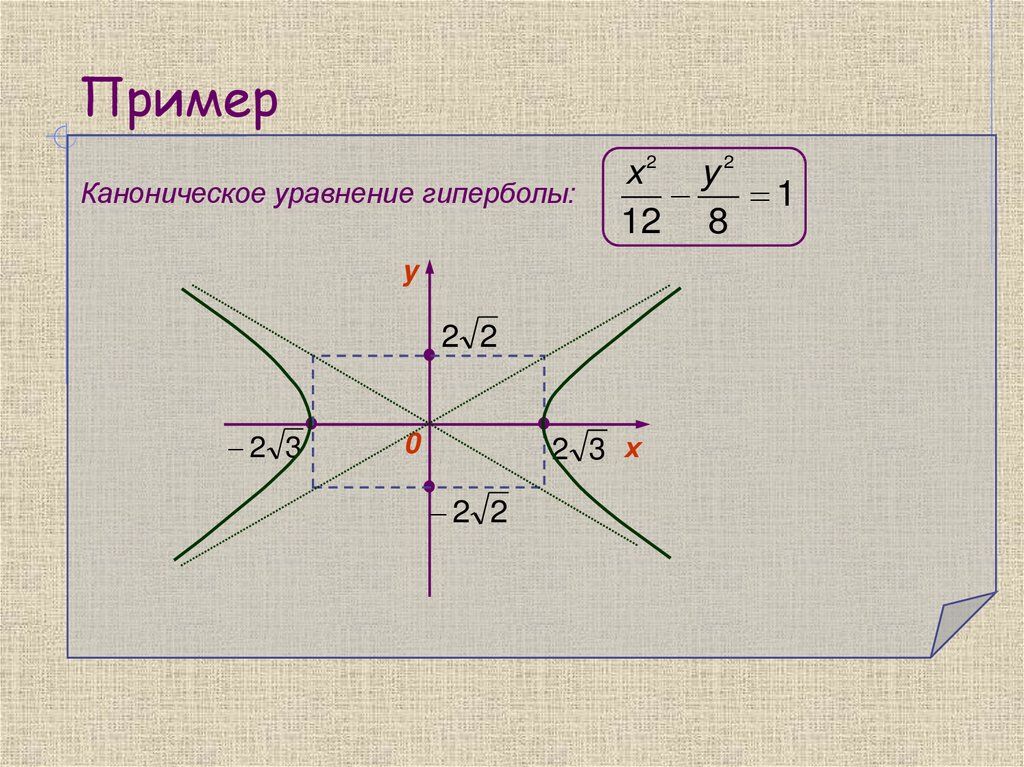
15. Пример

Каноническое уравнение гиперболы:
x2 y 2
1
12 8
y
2 2
2 3
2 3 х
0
2 2

16. Виды гипербол

Рассмотрим другие виды гипербол
Сопряженная гипербола
2
Y
c
2
x
y
1
2
2
a b
b
a X
b действительная полуось
a мнимая полуось
c
Равнобочная гипербола
x y a
2
2
2
2
x
y
или
2 1
2
a
a
2
Y
b
Гипербола со смещенным центром O ( x0 ; y0 )
'
( x x0 ) ( y y0 )
1
2
2
a
b
2
2
Гипербола, приведенная к своим асимптотам
xy a
или
a
y
x
X
a
O'
Y
X

17. Парабола

Параболой называется геометрическое место точек на
плоскости, для каждой из которых расстояние до некоторой
фиксированной точки той же плоскости
p
p
x
,
называемой
фокусом,
равно
расстоянию
до
прямой:
F ( ;0)
2
2
y
r d
d
M(x; y)
r
p
2
0
p
2
p 0
2
F
p
F ( ; 0)
2
х
p
r FM x y 2
2
d x
p
2

18. Парабола

каноническое
уравнение параболы
2
p
p
2
x
y
x
2
2
2
2
p
p
x 2 px
y 2 x 2 px
4
4
y
d
y 2 2px
директриса параболы
p
r x
2
M(x; y)
r
F
p
2
0
p
2
х
фокус параболы
Эксцентриситет параболы:
1

19.

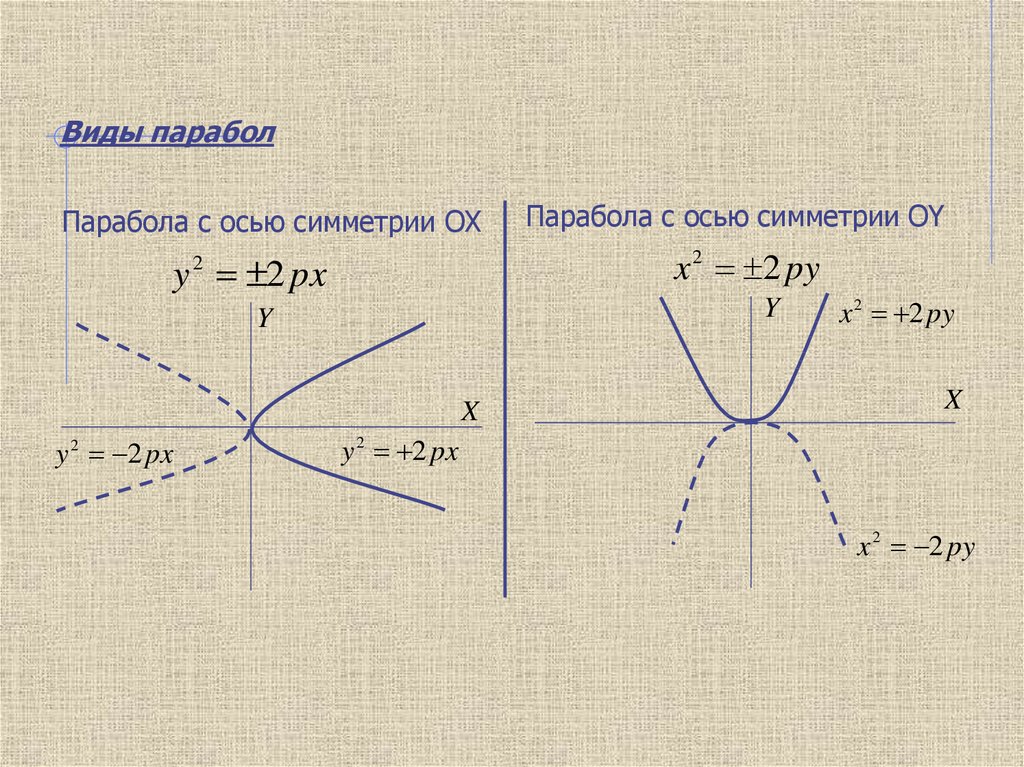
Виды парабол
Парабола с осью симметрии OX
x 2 2 py
y 2 px
2
Y
Y
X
y 2 2 px
Парабола c осью симметрии OY
x 2 2 py
X
y 2 2 px
x 2 2 py

20.

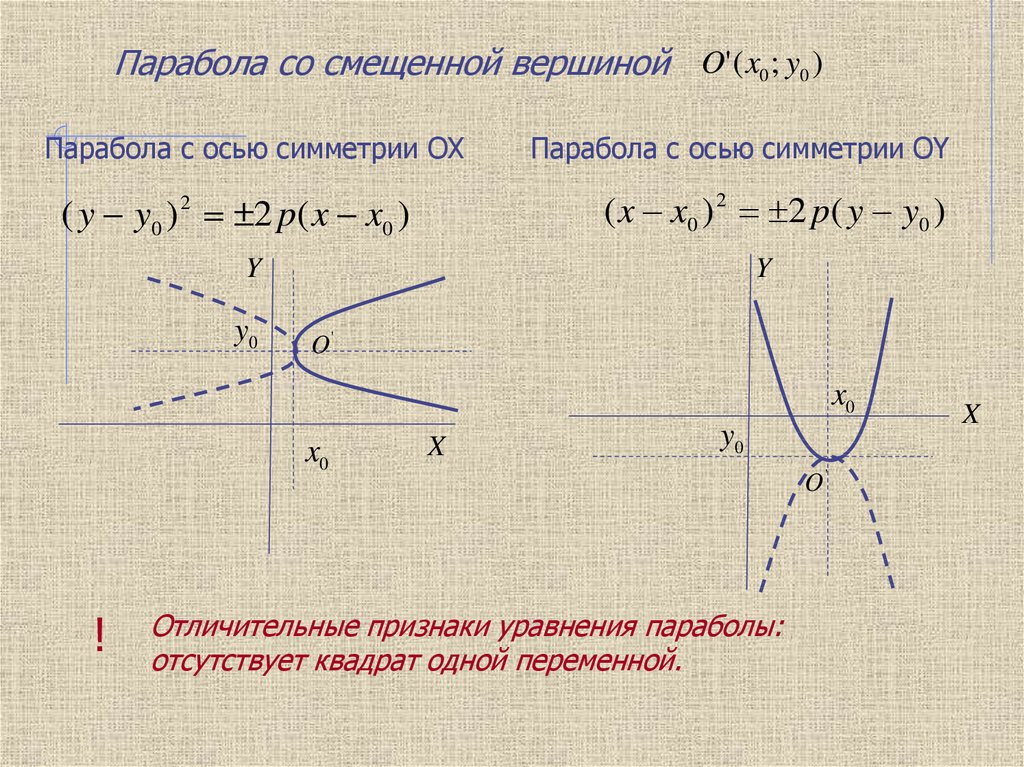
Парабола со смещенной вершиной O' ( x0 ; y0 )
Парабола с осью симметрии OX
Парабола c осью симметрии OY
( x x0 ) 2 2 p( y y0 )
( y y0 ) 2 2 p( x x0 )
Y
y0
Y
O'
x0
x0
!
X
y0
Отличительные признаки уравнения параболы:
отсутствует квадрат одной переменной.
O'
X

21. Построение парабол

Для построения параболы нужно знать:
Координаты вершины O' ( x0 ; y0 ) .
Ось симметрии параболы (определяется по той переменно,
квадрат которой отсутствует в уравнении)
Направление ветвей (определяется по знаку : если в правой
части канонического уравнения знак плюс, то ветви параболы
идут в положительном направлении оси симметрии, если знак
минус, то в отрицательном )
Параметр параболы p определяется по коэффициенту при
переменной, стоящей в каноническом уравнении в первой
степени, и определяет «ширину» параболы. Знание параметра
помогает более качественно получить начальный участок
параболы.

22.

2
(
y
2
)
4( x 1)
1. Построить параболу
Данное уравнение является каноническим уравнением параболы,
так как отсутствует квадрат переменной x . Поэтому осью
симметрии параболы будет ось OX.
Вершина параболы в точке O' (1;2)
Ветви параболы направлены в положительном направлении оси OX,
так как в правой части уравнения знак “плюс”.
2 p 4 ширина параболы
p 2 параметр параболы
p
1
2
Y
p
2
O' p p
2
1
X

23.

3. Построить кривую
y 2 x2
Преобразуем уравнение
x2 2 y
x 2 ( y 2)
Уравнение определяет параболу. Сравнивая с уравнением
( x x0 ) 2 2 p( y y0 ) , определяем координаты вершины
O' (0;2) . Ось симметрии OY. Ветви направлены вниз.
1 параметр параболы
p
2
Y
O' 2
p
1
2
1 1
O
X

24.

4. Построить параболу
4x2 6x 3y 2 0
В уравнении отсутствует квадрат переменной y, поэтому оно
определяет параболу с осью симметрии OY.
Проведем преобразования уравнения, чтобы привести его к
каноническому виду ( x x0 ) 2 2 p ( y y0 )
6
4 x 2 x 3 y 2 0
4
3
2
4 x 2 x (3 / 4) 2 (3 / 4) 2 3 y 2 0
4
2
3 9
3
9
4 x 3 y 2 0
4 x 3 y 2 0
4 4
4 16
Y
2
3
O ' y0
1
4 x 3 y
4
4
X
x0 O
2
3
1
4 x 3 y или
4
12
2
3
3
1
x y
4
4
12
3
3 1
O ' ; вершина параболы p параметр параболы
8
4 12
Ветви параболы направлены вниз
2