Похожие презентации:
Законы алгебры логики. Равносильные преобразования
1.
2. Равносильные преобразования
• Равносильные преобразования логическихформул имеют то же назначение, что и
преобразования формул в обычной алгебре.
• Они служат для упрощения формул или
приведения их к определённому виду путем
использования основных законов алгебры
логики.
3.
Под упрощением формулы, понимаютравносильное преобразование,
приводящее к формуле, которая
• либо содержит по сравнению с исходной
меньшее число операций конъюнкции и
дизъюнкции и инверсий
• не содержит отрицаний неэлементарных
формул, либо содержит их меньшее число
4. Равносильность формул
• Две формулы F и G называютсяравносильными, если на любом наборе
пропозиционных переменных λ(F) =
λ(G).
• Обозначения: F ≡ G.
5. 1. Закон двойного отрицания
Двойное отрицание исключаетотрицание.
A A
6. 2. Переместительный (коммутативный) закон
— для логического сложения:A B B A
— для логического умножения:
A& B B & A
7. 3. Сочетательный (ассоциативный) закон
— для логического сложения:( A B) C A ( B C )
— для логического умножения:
( A & B) & C A & ( B & C )
8. 4. Распределительный (дистрибутивный) закон
— для логического сложения:( A B) & ( A C ) A ( B & C )
— для логического умножения:
( A & B) ( A & C ) A & ( B C )
9. 5. Закон общей инверсии (законы де Моргана)
— для логического сложенияА В A & B
— для логического умножения:
А& В A B
10. 6. Закон идемпотентности
— для логического сложения:A A A
— для логического умножения:
A& A A
Закон означает отсутствие показателей степени.
11. 7. Законы исключения констант
— для логического сложения:А 0 A
А 1 1
— для логического умножения:
А &1 A
А&0 0
12. 8. Закон противоречия
Невозможно, чтобы противоречащиевысказывания были одновременно
истинными.
A&A 0
13. 9. Закон исключения третьего
Из двух противоречащих высказываний ободном и том же предмете одно всегда
истинно, а второе — ложно, третьего не дано.
A A 1
14. 10. Закон поглощения
— для логического сложения:— для логического умножения:
A & ( A B) A
15. 11. Закон исключения (склеивания)
— для логического сложения:( A B) * ( A B) B
— для логического умножения:
A* B A* B B















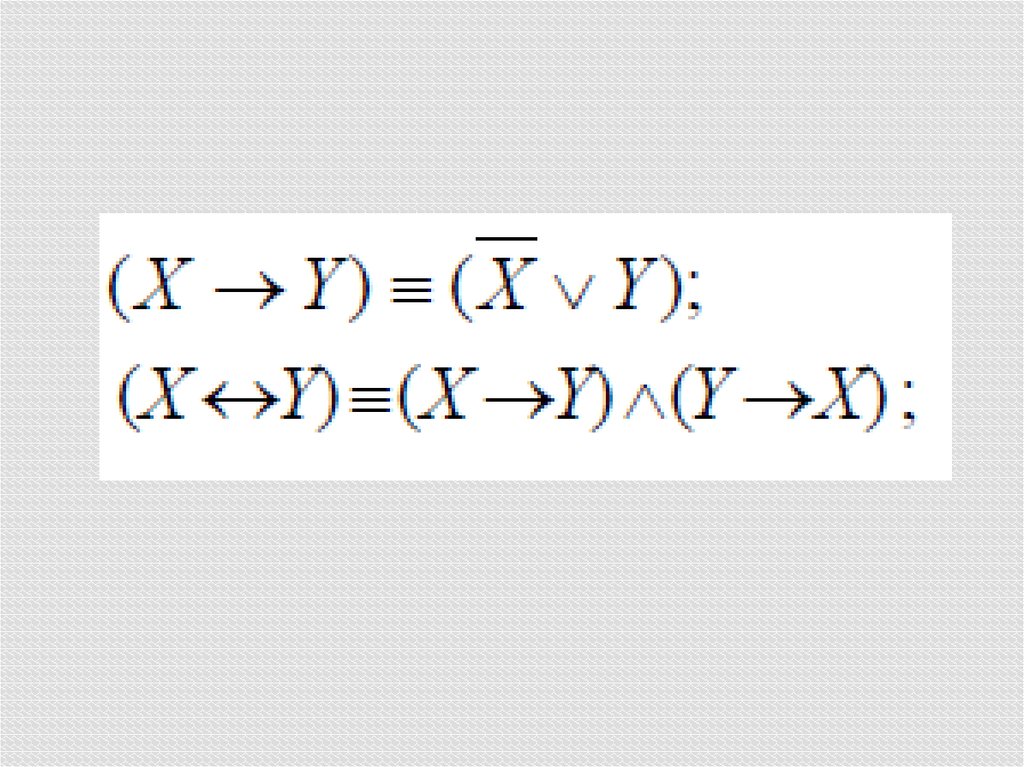
 Информатика
Информатика








