Кривые линии. Образование и задание поверхностей. (Лекция 3)

1. ЛЕКЦИЯ 3 Кривые линии. Образование и задание поверхностей.

Начертательная геометрия
1 семестр
для студентов ф-та ИУ
ЛЕКЦИЯ 3
Кривые линии.
Образование и задание поверхностей.
Подготовили:
доценты кафедры РК-1 Сенченкова Л.С., Палий Н.В.

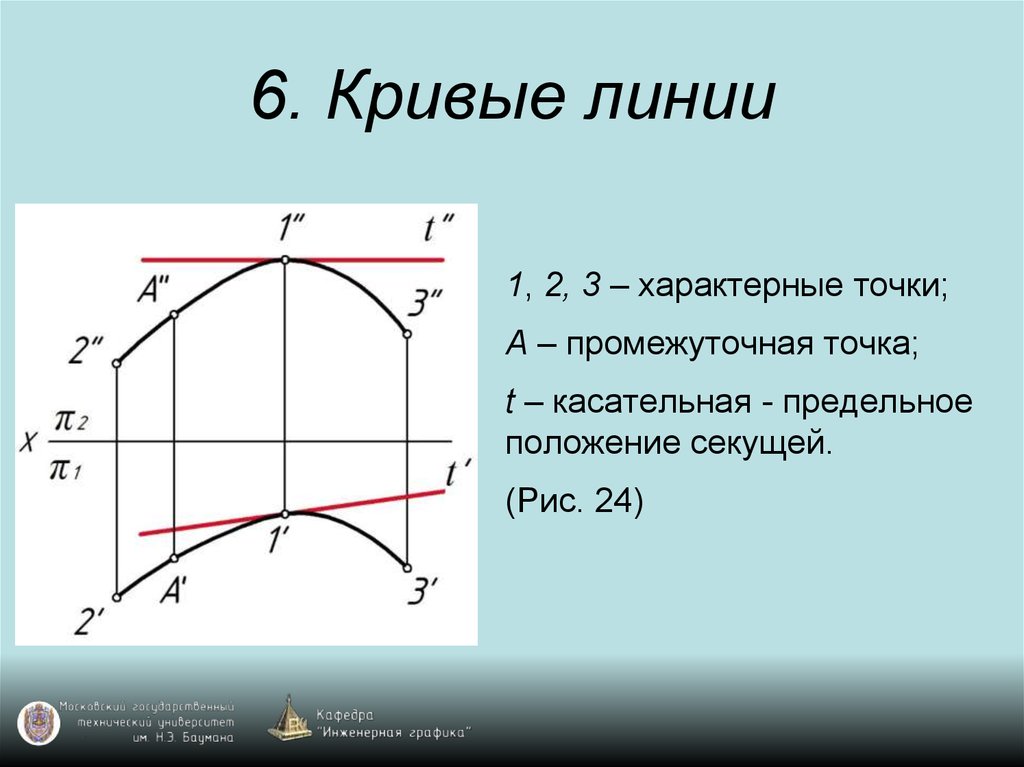
2. 6. Кривые линии

1, 2, 3 – характерные точки;
А – промежуточная точка;
t – касательная - предельное
положение секущей.
(Рис. 24)

3. Плоские кривые Проекции окружности (рис. 25)

4. Плоские кривые Проекции окружности (рис. 25)

5. Плоские кривые Проекции окружности (рис. 25)

6. Плоские кривые Проекции окружности (рис. 25)

7. Плоские кривые Проекции окружности (рис. 25)

8. Плоские кривые Проекции окружности (рис. 25)

9. Плоские кривые Проекции окружности (рис. 25)

10. Плоские кривые Проекции окружности (рис. 25)

11. Плоские кривые Проекции окружности (рис. 25)

12. Плоские кривые Проекции окружности (рис. 25)

13. Плоские кривые Проекции окружности (рис. 25)

14. Плоские кривые Проекции окружности (рис. 25)

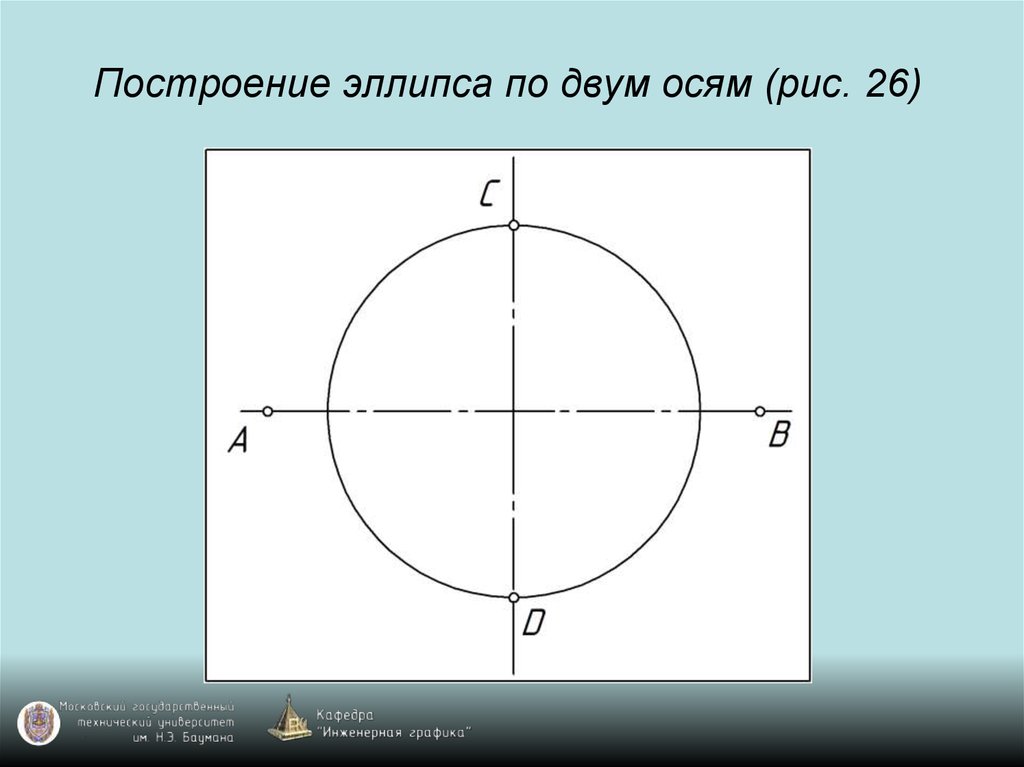
15. Построение эллипса по двум осям (рис. 26)

16. Построение эллипса по двум осям (рис. 26)

17. Построение эллипса по двум осям (рис. 26)

18. Построение эллипса по двум осям (рис. 26)

19. Построение эллипса по двум осям (рис. 26)

20. Построение эллипса по двум осям (рис. 26)

21. Построение эллипса по двум осям (рис. 26)

22. Построение эллипса по двум осям (рис. 26)

23. Построение эллипса по двум осям (рис. 26)

24. Построение эллипса по двум осям (рис. 26)

25. Построение эллипса по двум осям (рис. 26)

26. Построение эллипса по двум осям (рис. 26)

27. Построение эллипса по двум осям (рис. 26)

28. Построение эллипса по двум осям (рис. 26)

29. Пространственные кривые Винтовая линия

Винтовая линия образуется при винтовом движении точки, т.е. при повороте
точки вокруг неподвижной оси и одновременном перемещении точки вдоль оси.

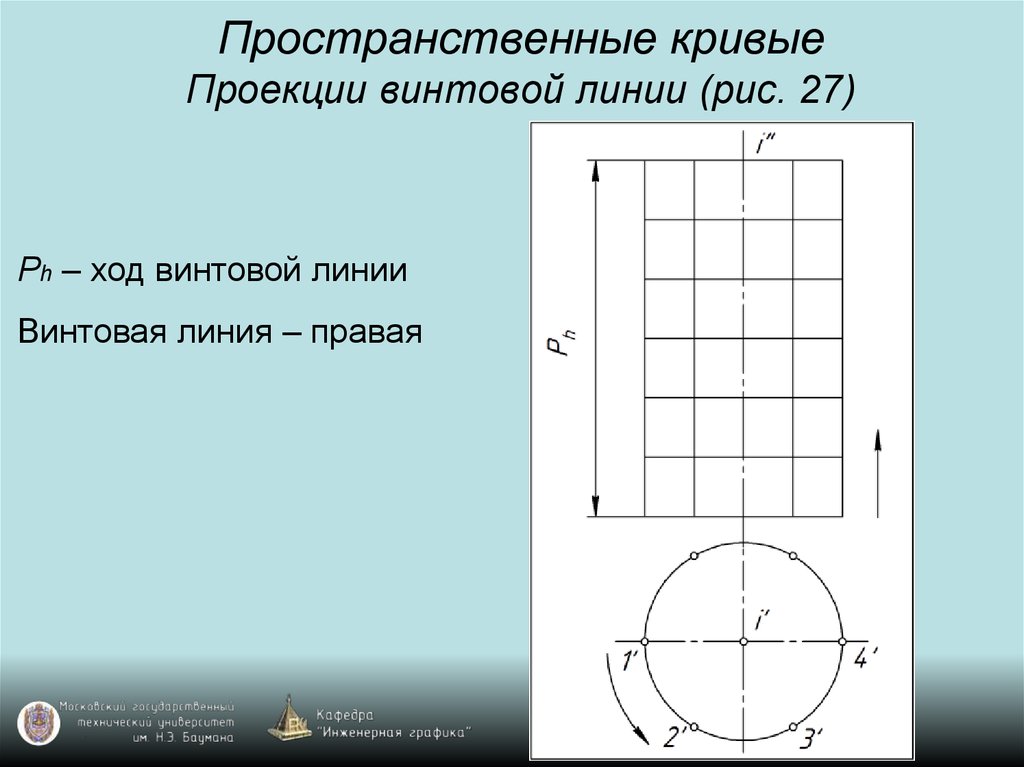
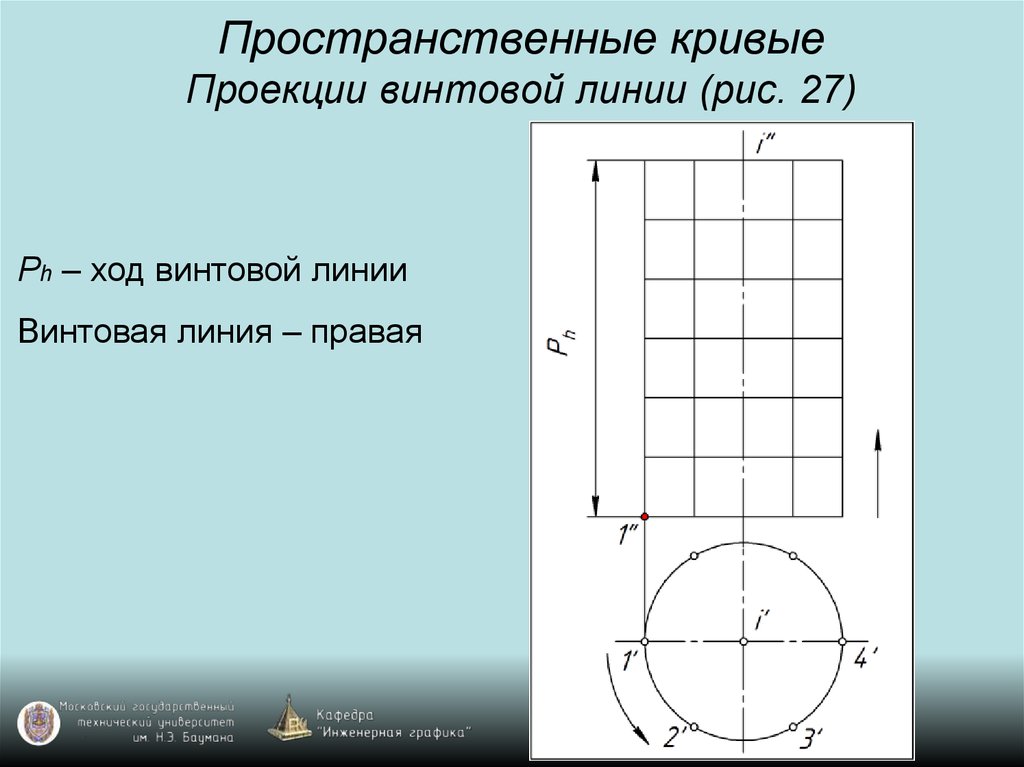
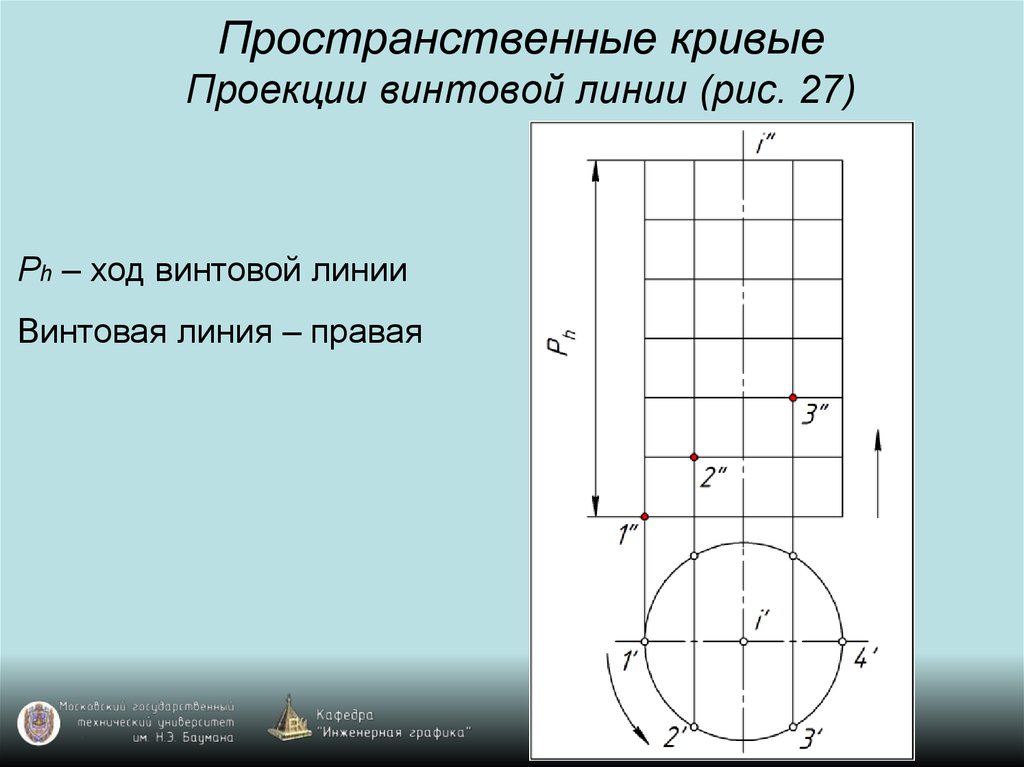
30. Пространственные кривые Проекции винтовой линии (рис. 27)

Ph – ход винтовой линии
Винтовая линия – правая

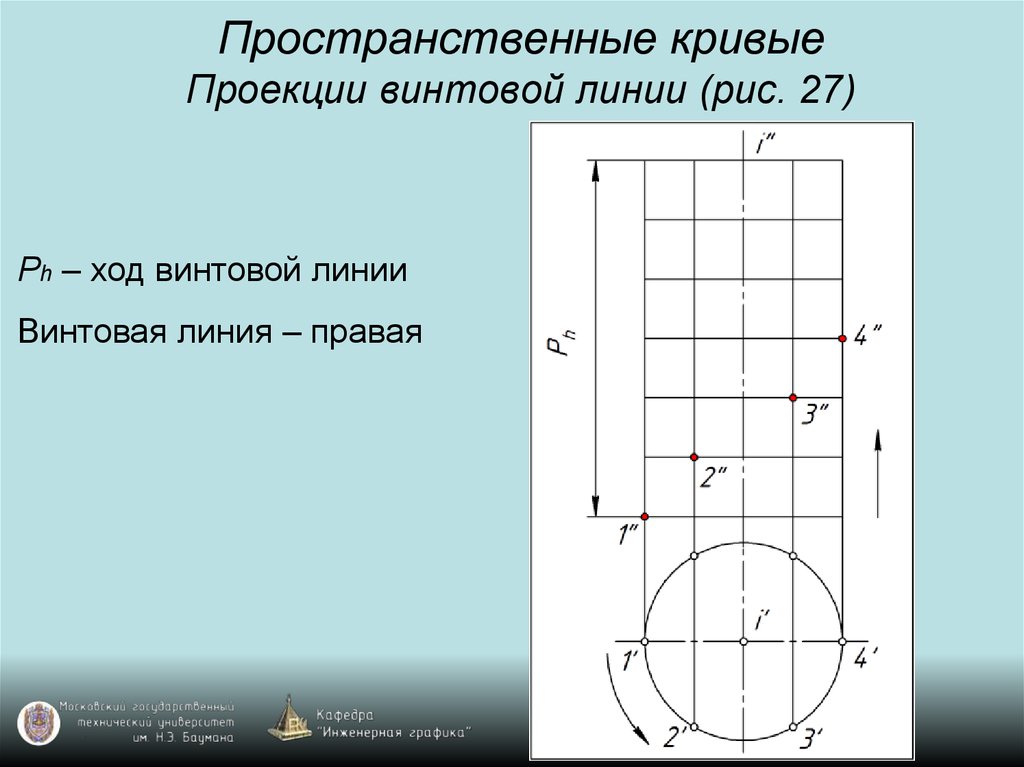
31. Пространственные кривые Проекции винтовой линии (рис. 27)

Ph – ход винтовой линии
Винтовая линия – правая

32. Пространственные кривые Проекции винтовой линии (рис. 27)

Ph – ход винтовой линии
Винтовая линия – правая

33. Пространственные кривые Проекции винтовой линии (рис. 27)

Ph – ход винтовой линии
Винтовая линия – правая

34. Пространственные кривые Проекции винтовой линии (рис. 27)

Ph – ход винтовой линии
Винтовая линия – правая

35. Пространственные кривые Проекции винтовой линии (рис. 27)

Ph – ход винтовой линии
Винтовая линия – правая

36. Пространственные кривые Проекции винтовой линии (рис. 27)

Ph – ход винтовой линии
Винтовая линия – правая

37. Пространственные кривые Проекции винтовой линии (рис. 27)

Ph – ход винтовой линии
Винтовая линия – правая

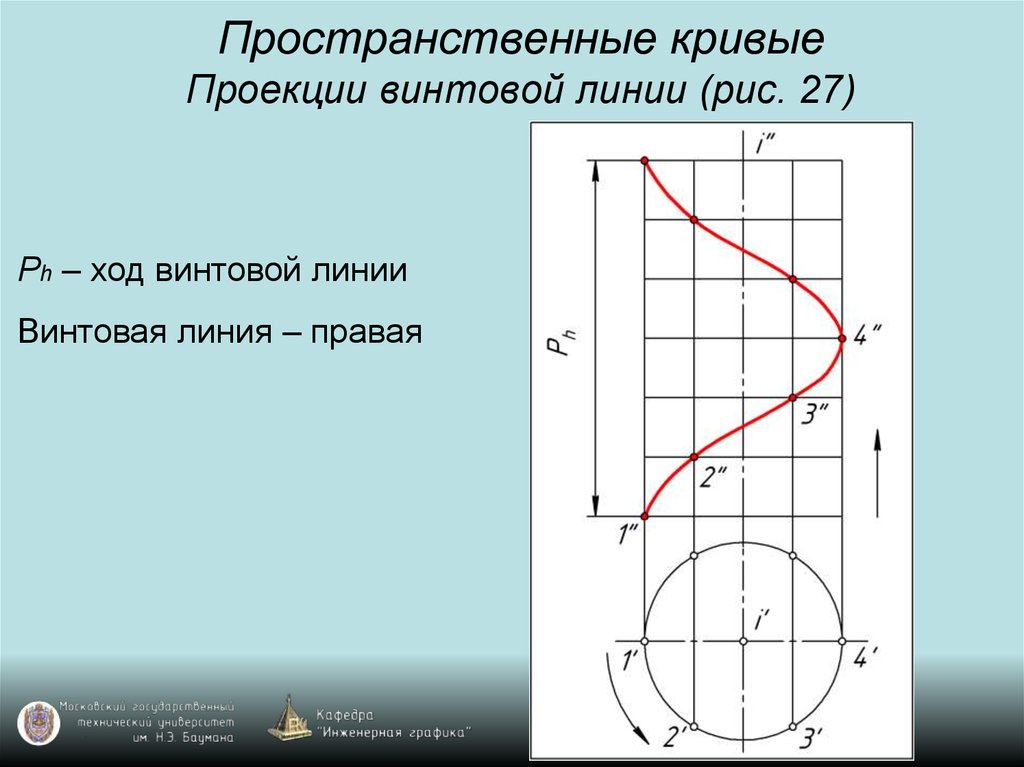
38. Пространственные кривые Проекции винтовой линии (рис. 27)

Ph – ход винтовой линии
Винтовая линия – правая

39. 7. Образование и задание поверхностей

Задание поверхности с
помощью направляющих d
и образующих g (рис. 28)
Задание поверхности с
помощью каркаса (рис. 29)

40. Очерк поверхности

Для большей наглядности в ряде случаев используют очерк
поверхности (рис. 30).

41. Общее правило построения проекции точки, принадлежащей поверхности:

Для построения проекции точки, принадлежащей
поверхности, надо воспользоваться проекциями
линии, принадлежащей поверхности и
проходящей через заданную точку.

42. Обзор поверхностей

Можно группировать поверхности:
- по форме образующей: линейчатые,
нелинейчатые;
- по движению образующей: параллельный
перенос, вращение, винтовое;
- по возможности развернуть на плоскость:
развертываемые, неразвертываемые.

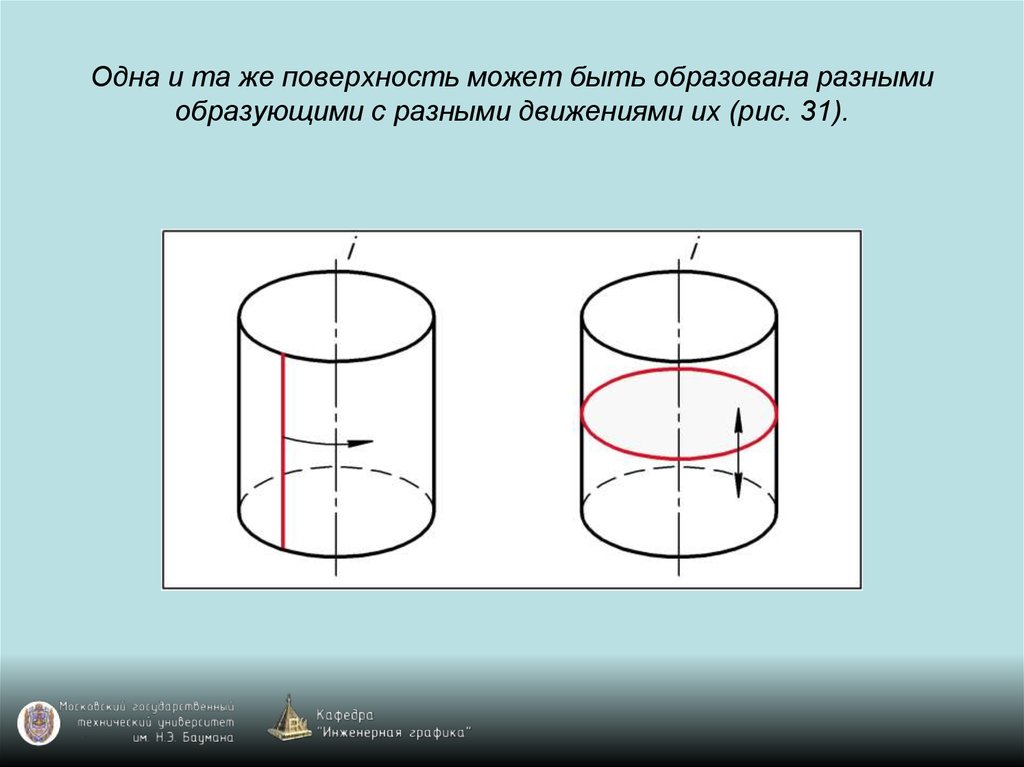
43. Одна и та же поверхность может быть образована разными образующими с разными движениями их (рис. 31).

44. Одна и та же поверхность может быть образована разными образующими с разными движениями их (рис. 31).

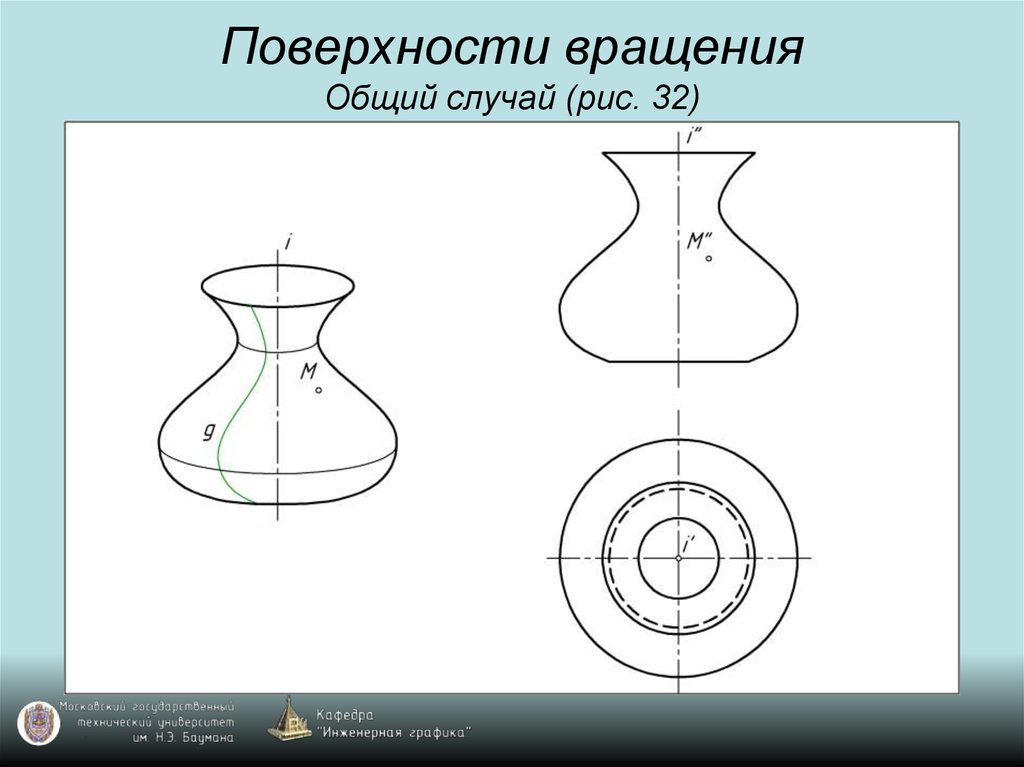
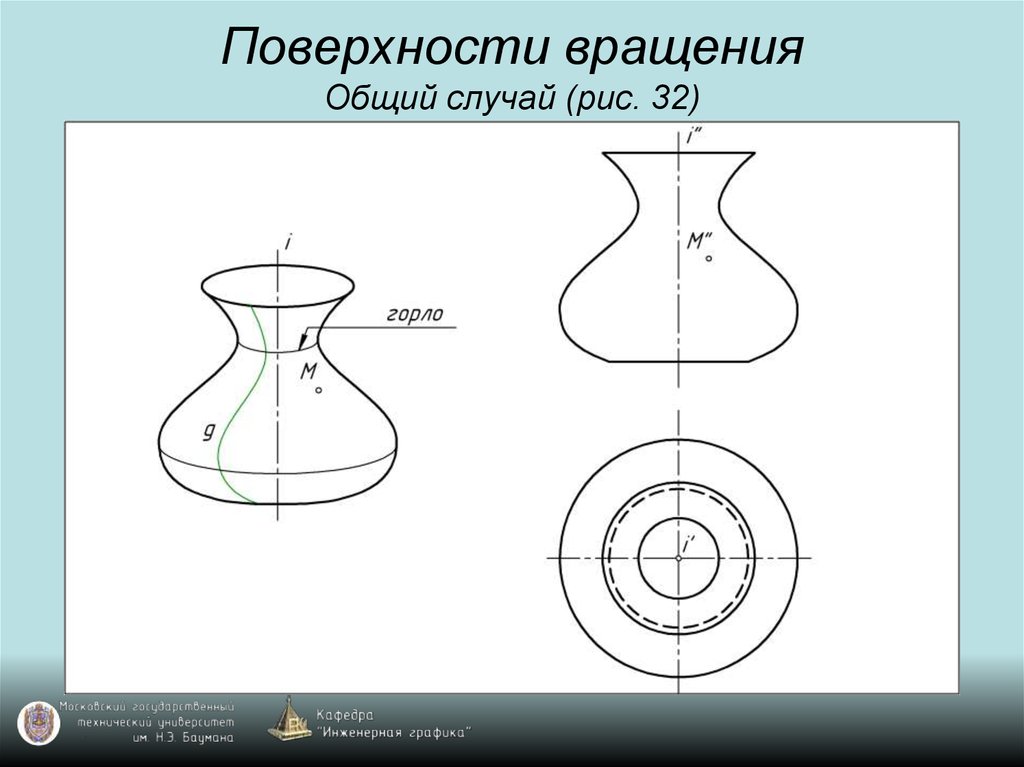
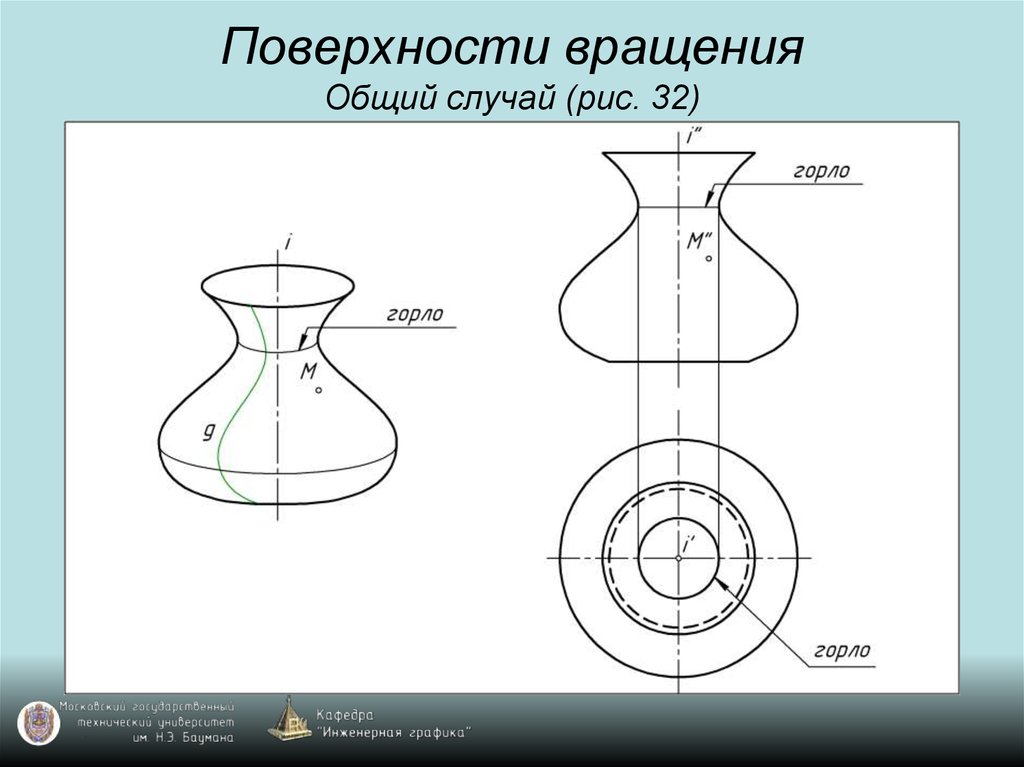
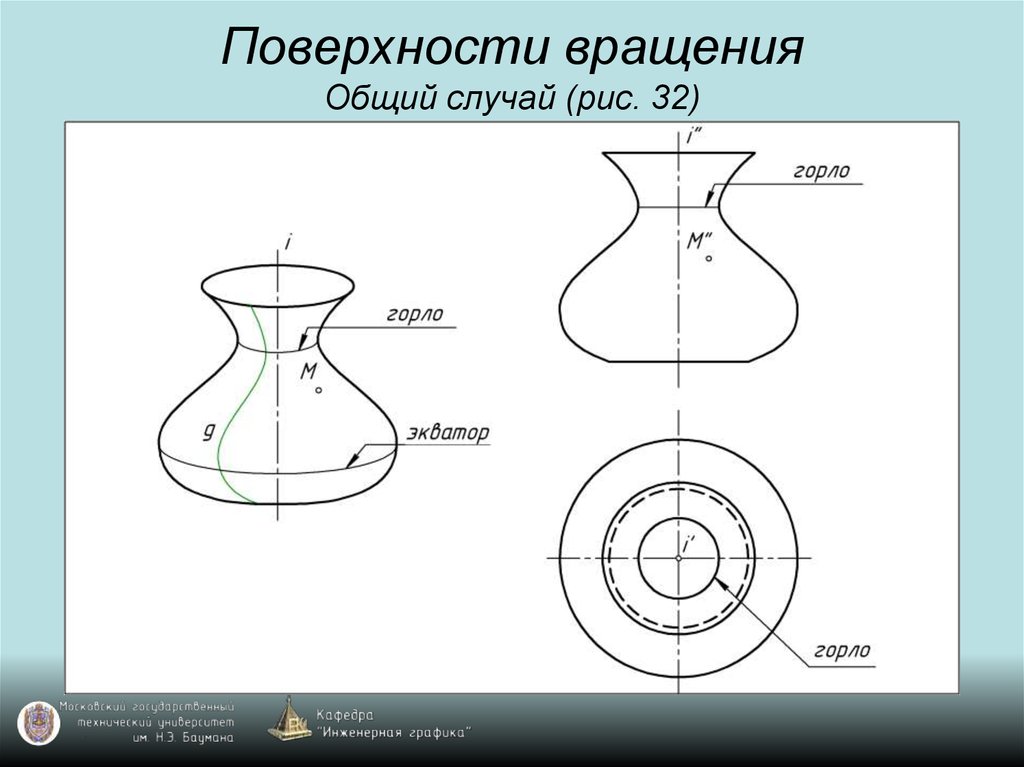
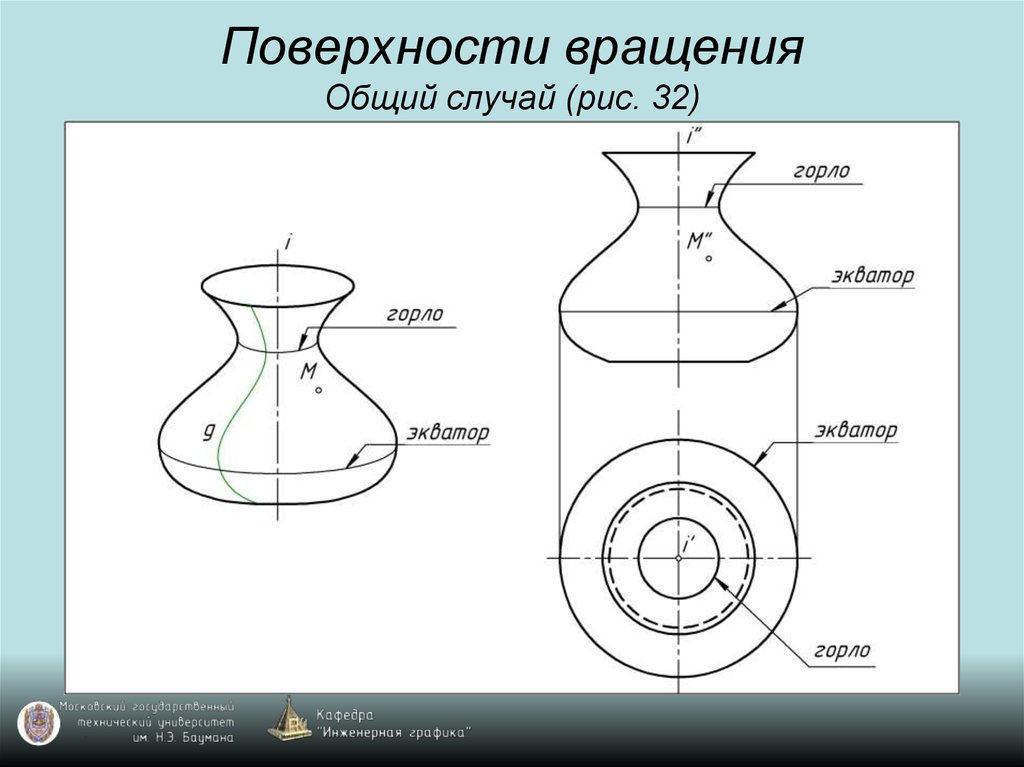
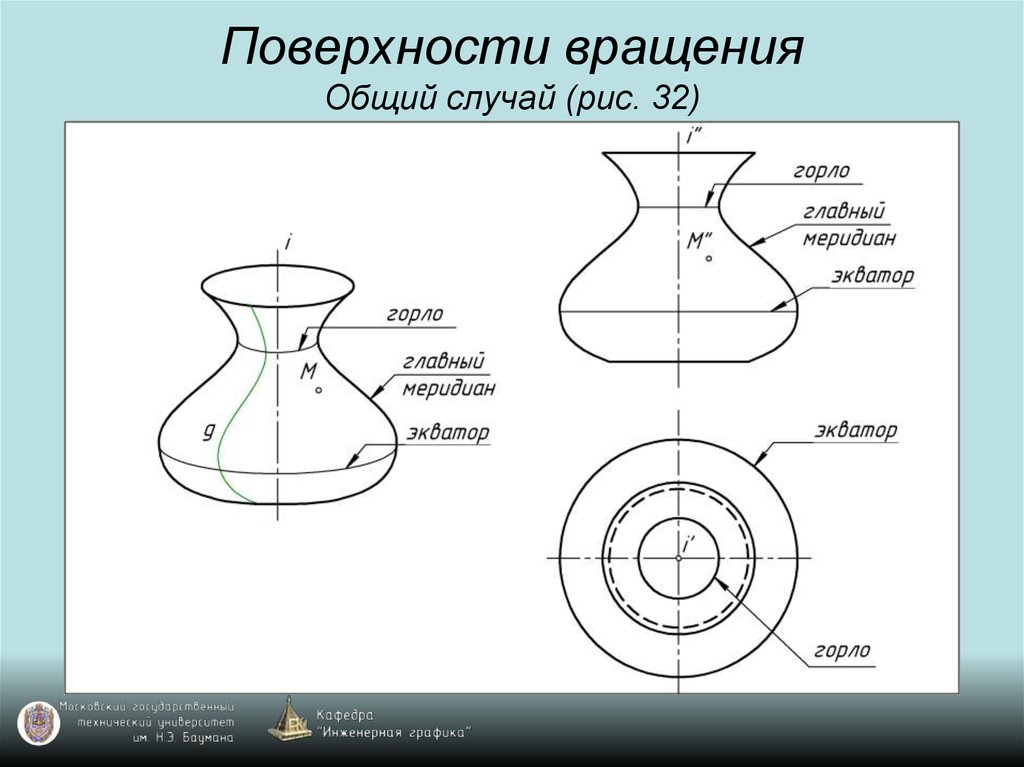
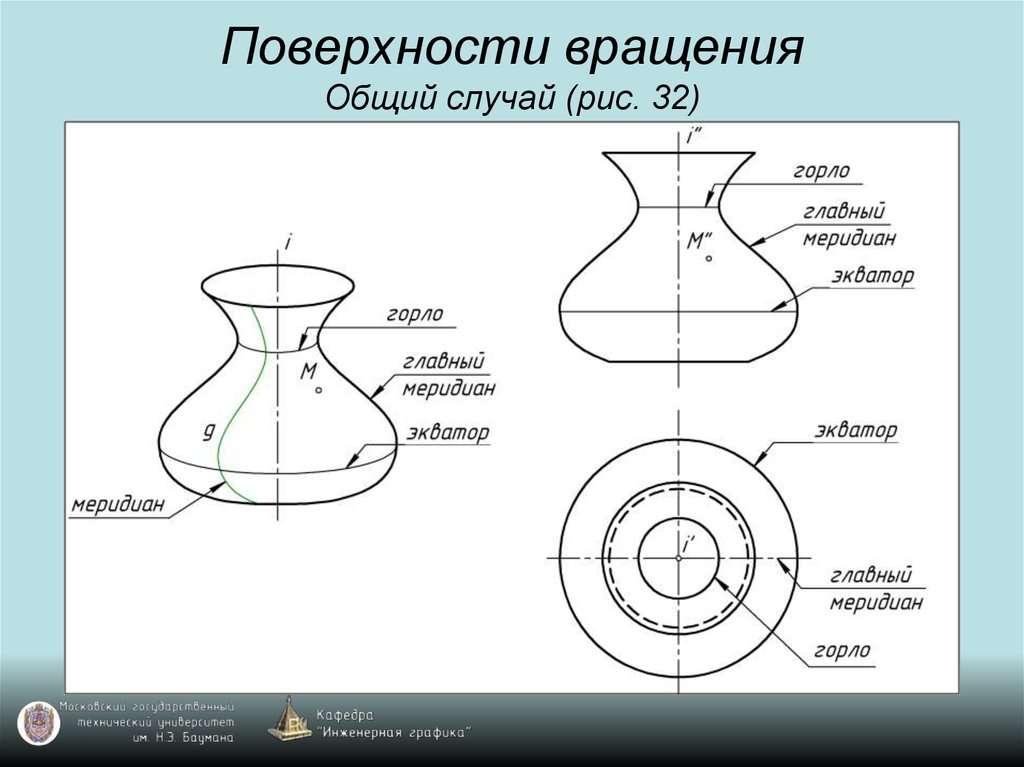
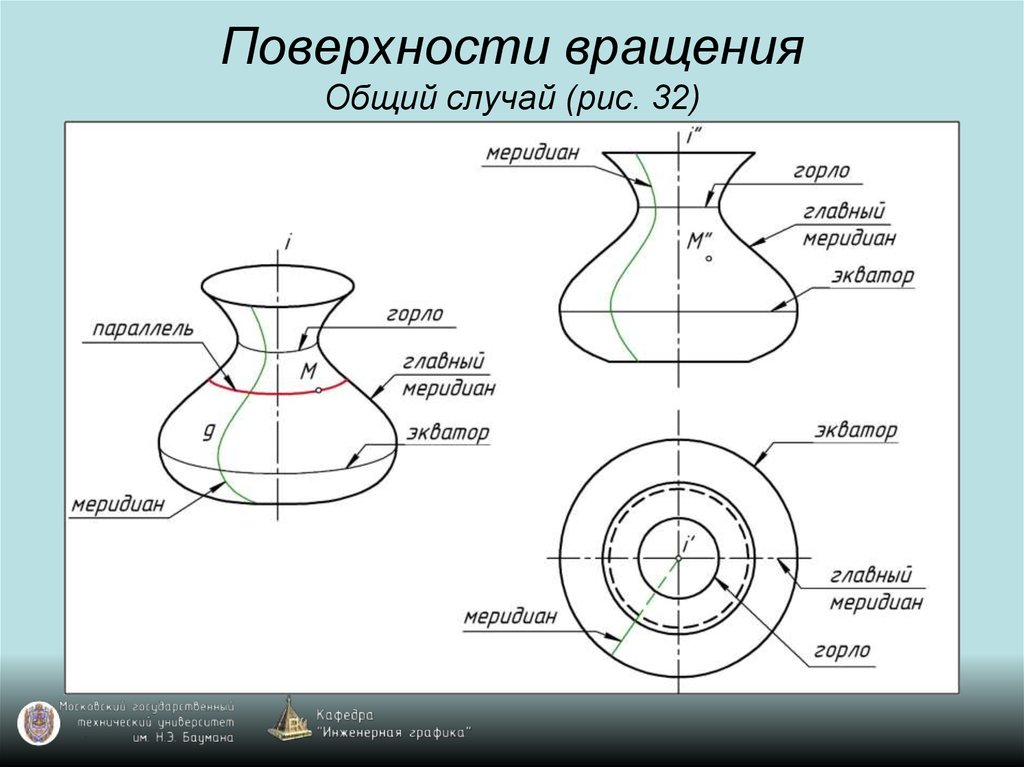
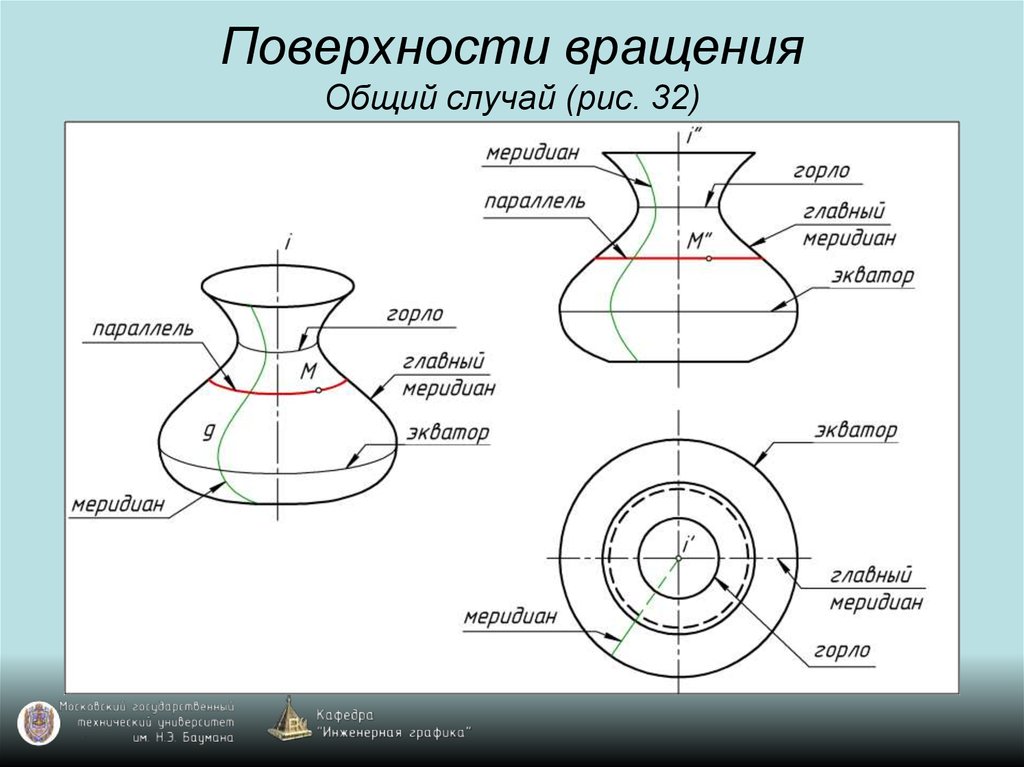
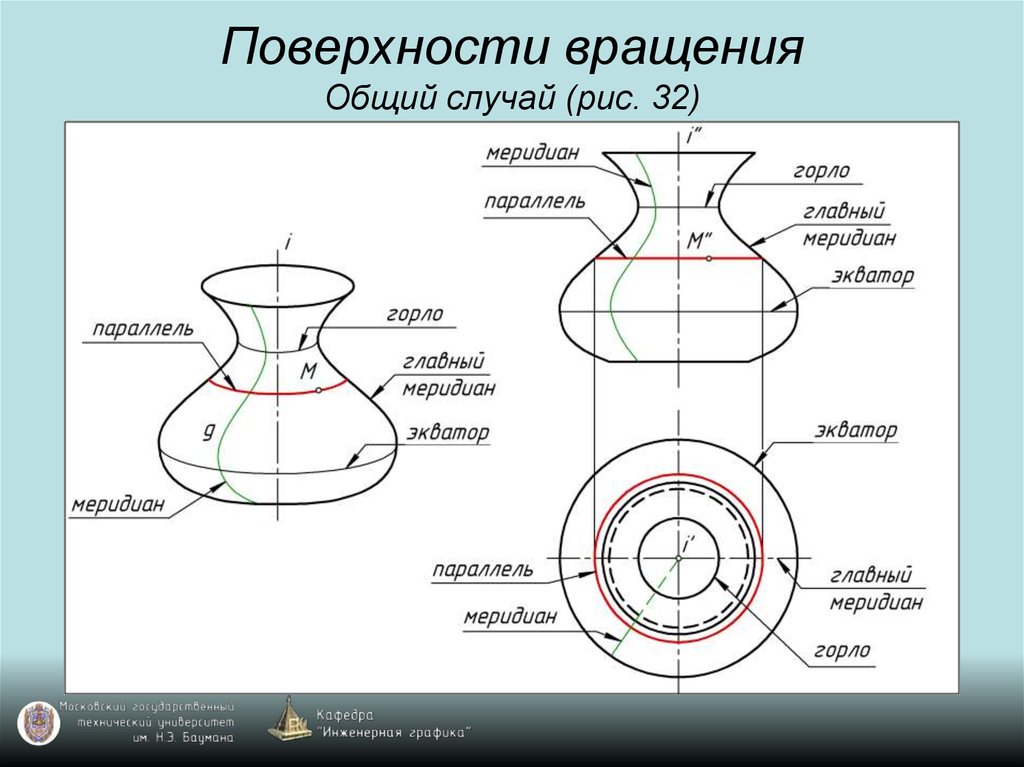
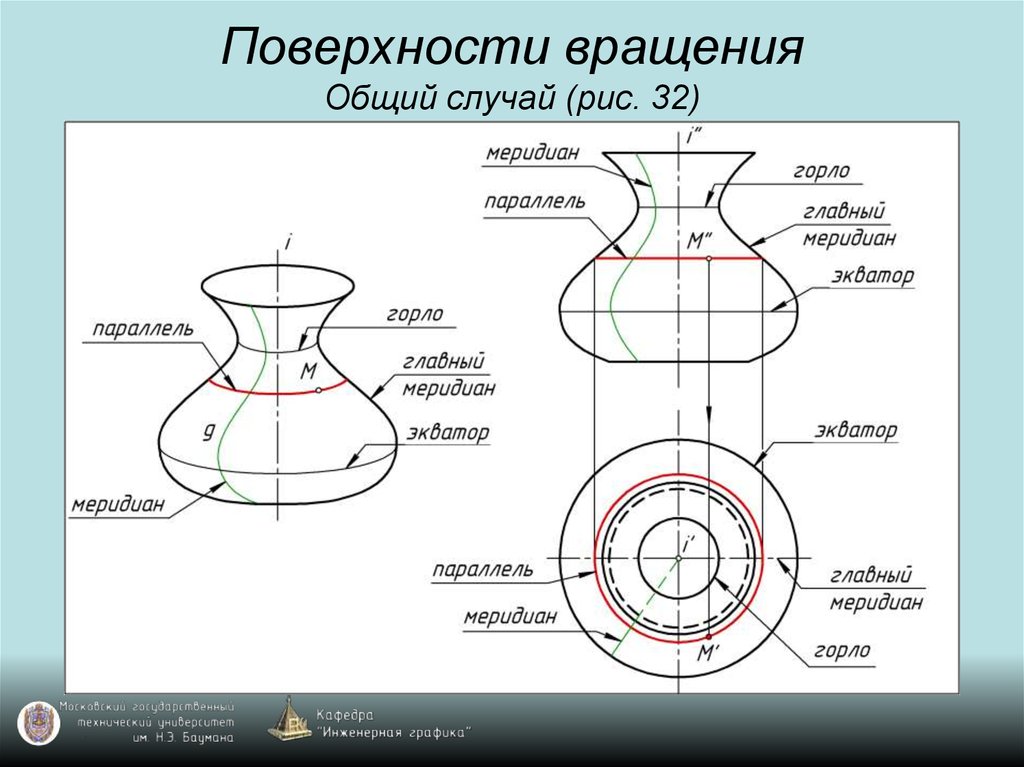
45. Поверхности вращения Общий случай (рис. 32)

46. Поверхности вращения Общий случай (рис. 32)

47. Поверхности вращения Общий случай (рис. 32)

48. Поверхности вращения Общий случай (рис. 32)

49. Поверхности вращения Общий случай (рис. 32)

50. Поверхности вращения Общий случай (рис. 32)

51. Поверхности вращения Общий случай (рис. 32)

52. Поверхности вращения Общий случай (рис. 32)

53. Поверхности вращения Общий случай (рис. 32)

54. Поверхности вращения Общий случай (рис. 32)

55. Поверхности вращения Общий случай (рис. 32)

56. Поверхности вращения Общий случай (рис. 32)

57. Поверхности вращения Общий случай (рис. 32)

58. Поверхности вращения Общий случай (рис. 32)

59. Поверхности вращения Общий случай (рис. 32)

60. Поверхности вращения Общий случай (рис. 32)

61. Поверхности вращения Общий случай (рис. 32)

62. Поверхности вращения Общий случай (рис. 32)

63. Поверхности вращения Общий случай (рис. 32)

64. Поверхности вращения Общий случай (рис. 32)

65. Поверхности вращения с образующей g – прямой линией. Укажите положение образующей g относительно оси i (рис. 33).

66. Поверхности вращения с образующей g – прямой линией. Укажите положение образующей g относительно оси i (рис. 33).

67. Поверхности вращения с образующей g – прямой линией. Укажите положение образующей g относительно оси i (рис. 33).

68. Поверхности вращения с образующей g – прямой линией. Укажите положение образующей g относительно оси i (рис. 33).

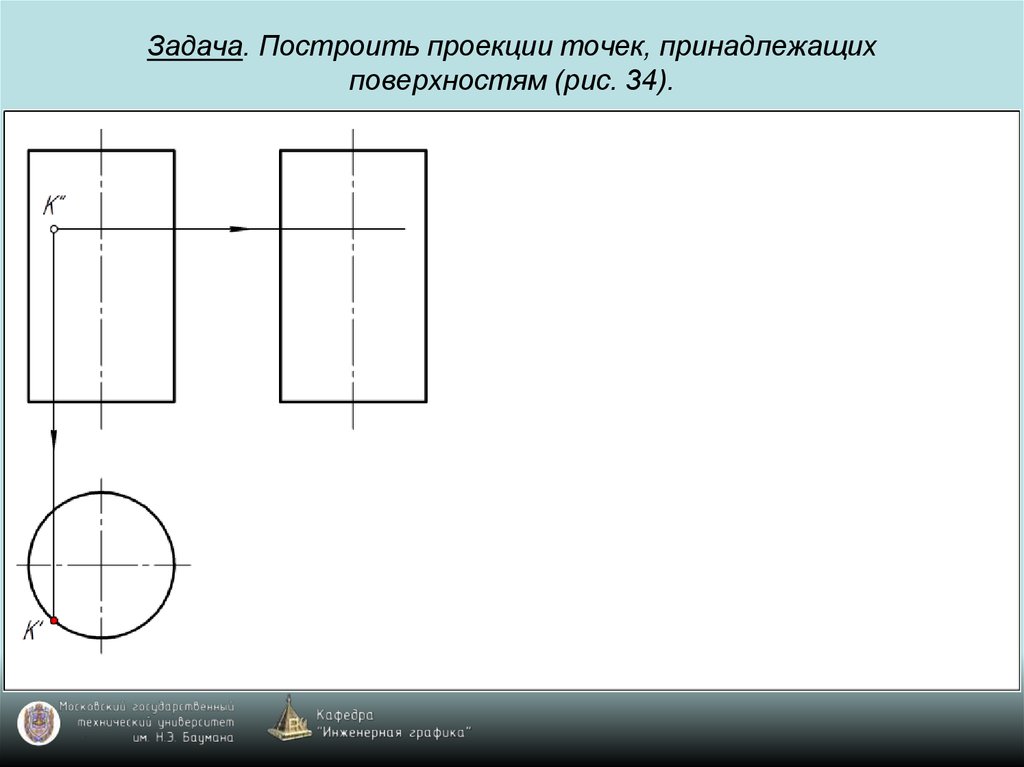
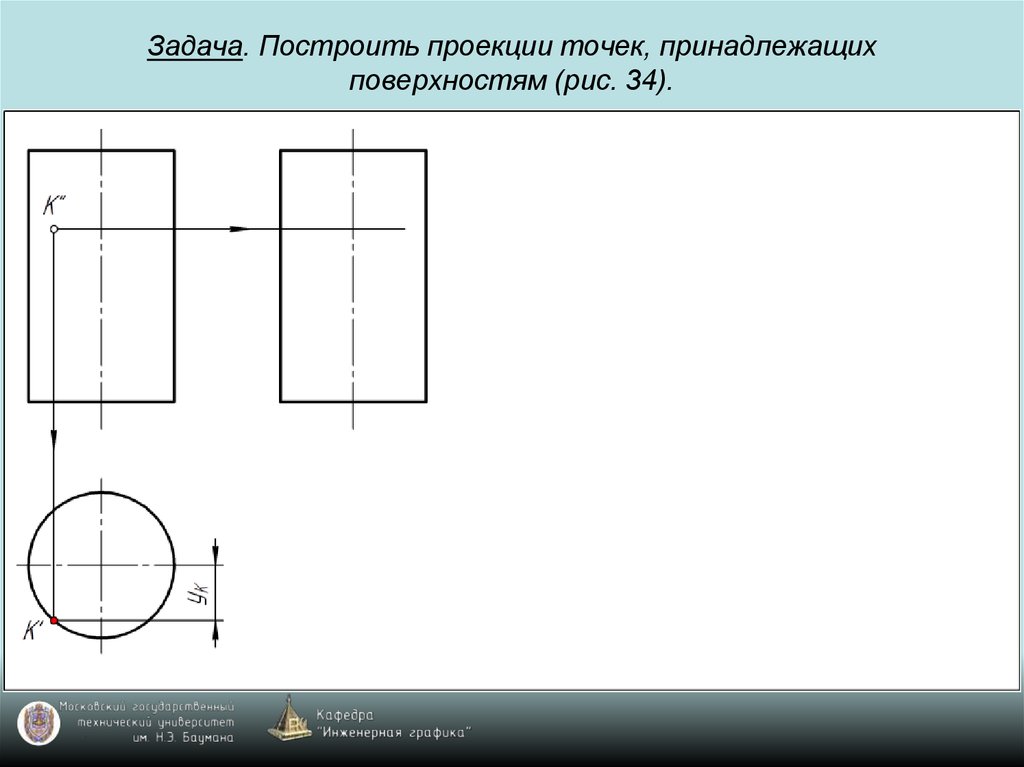
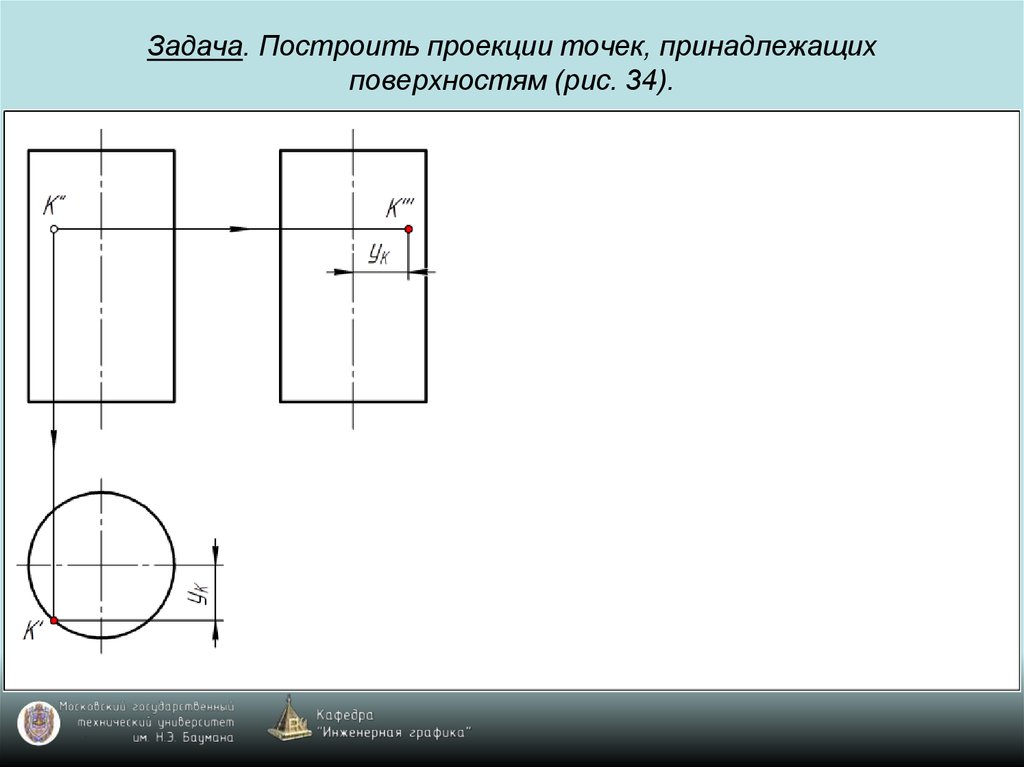
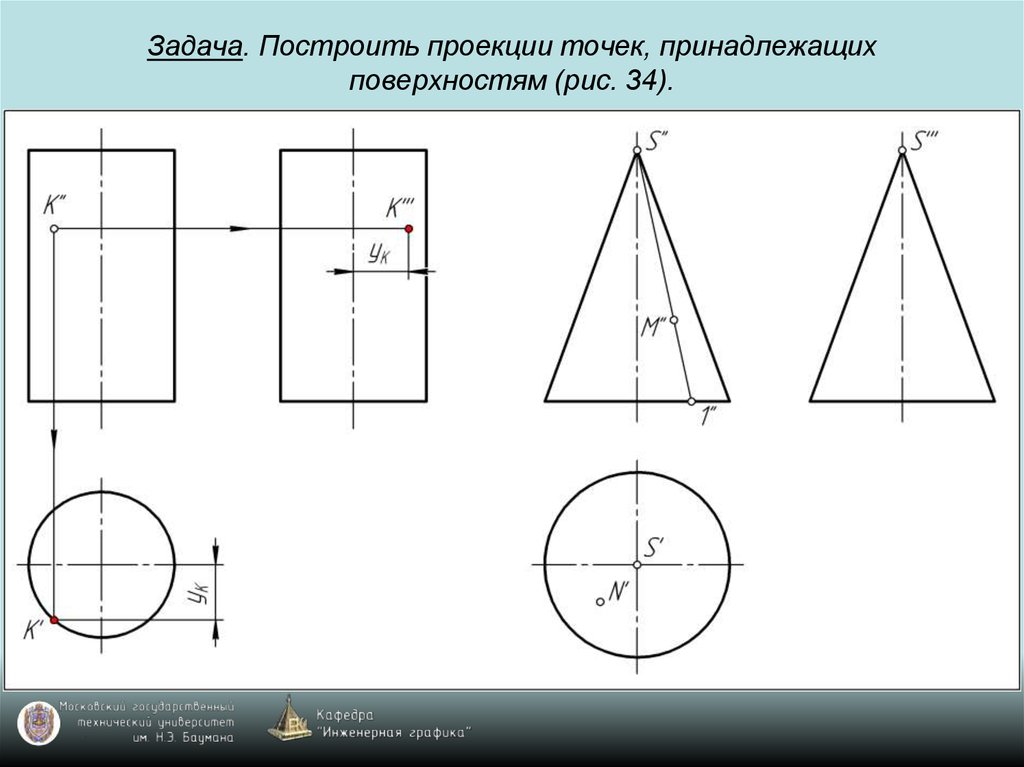
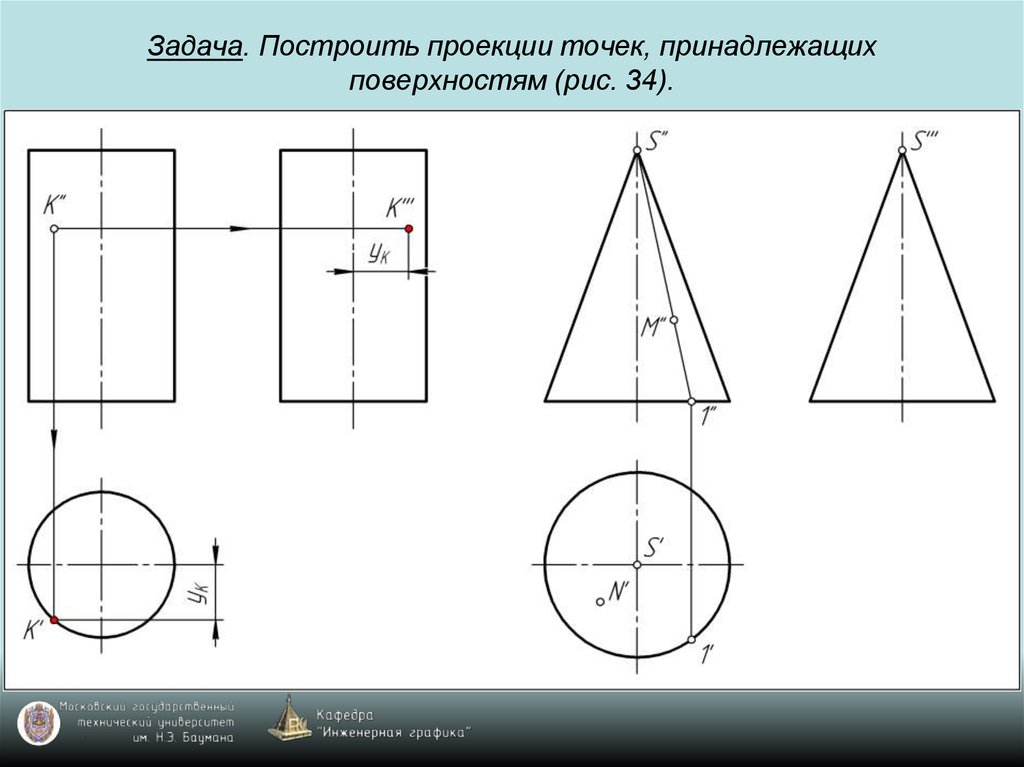
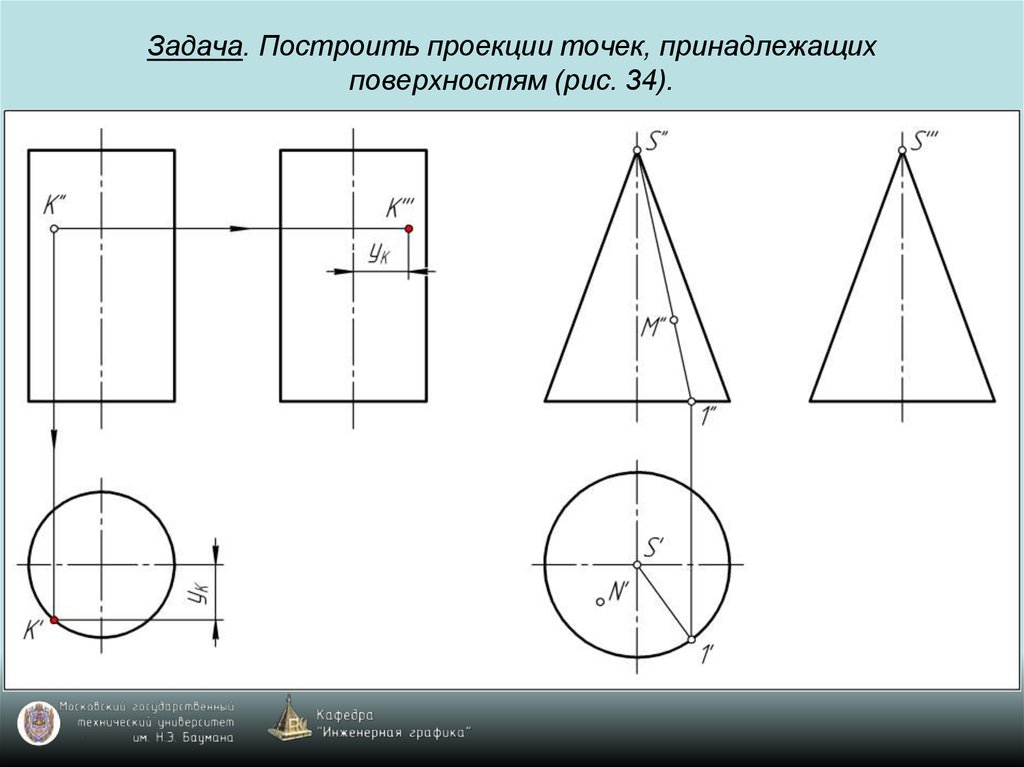
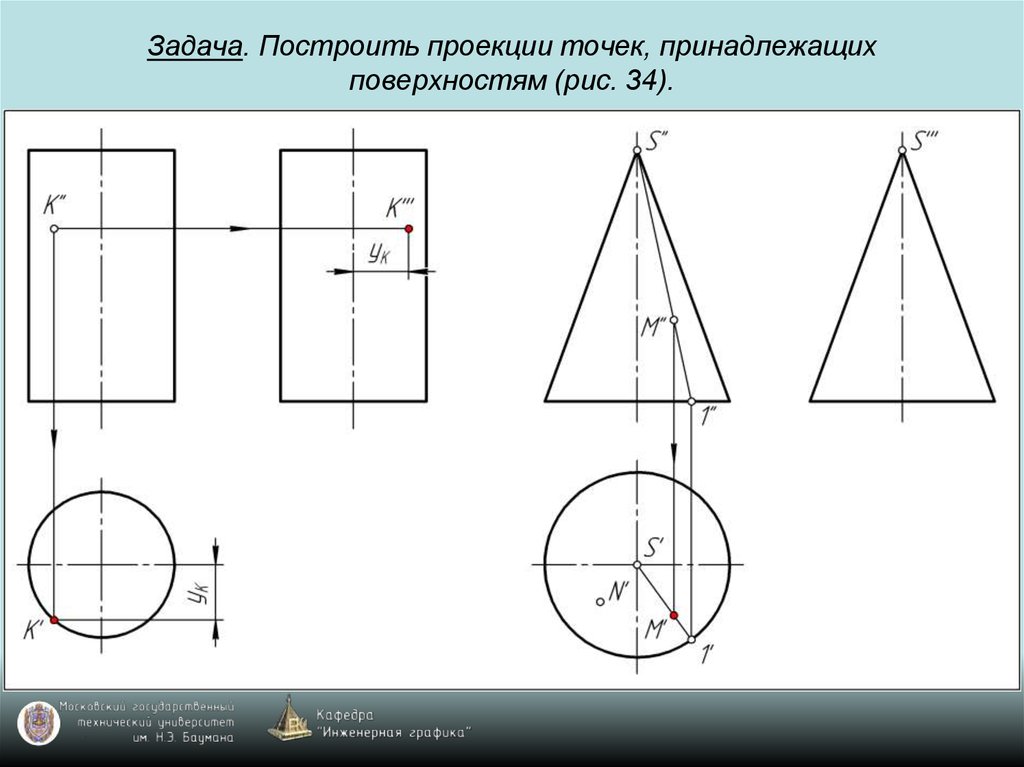
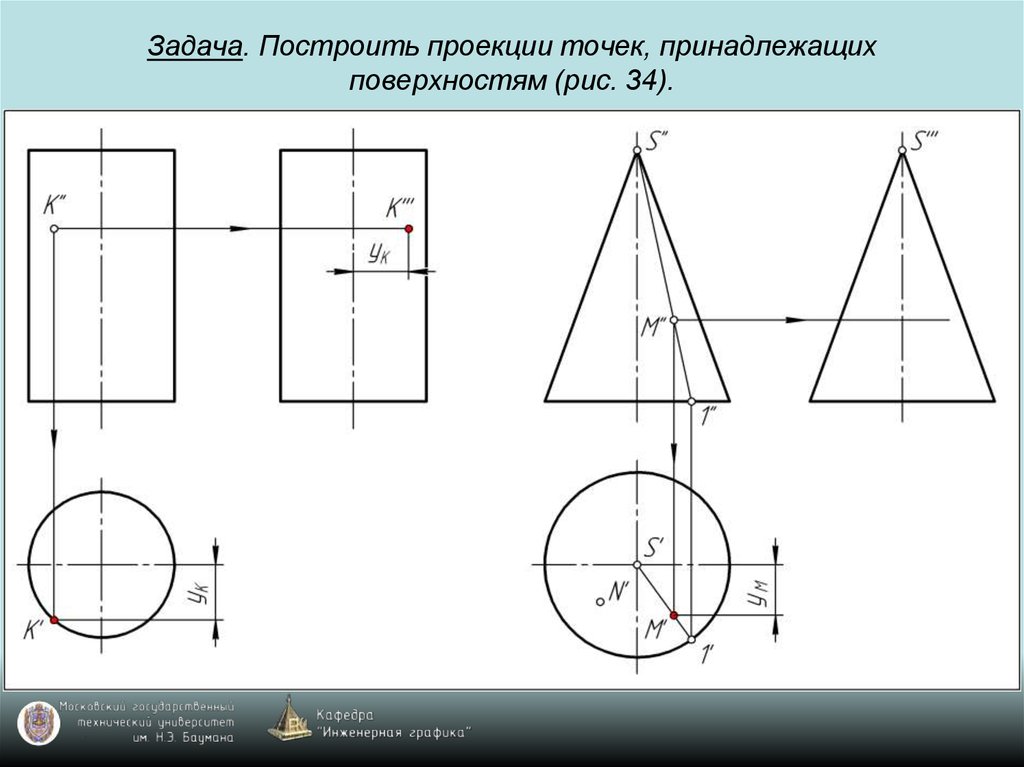
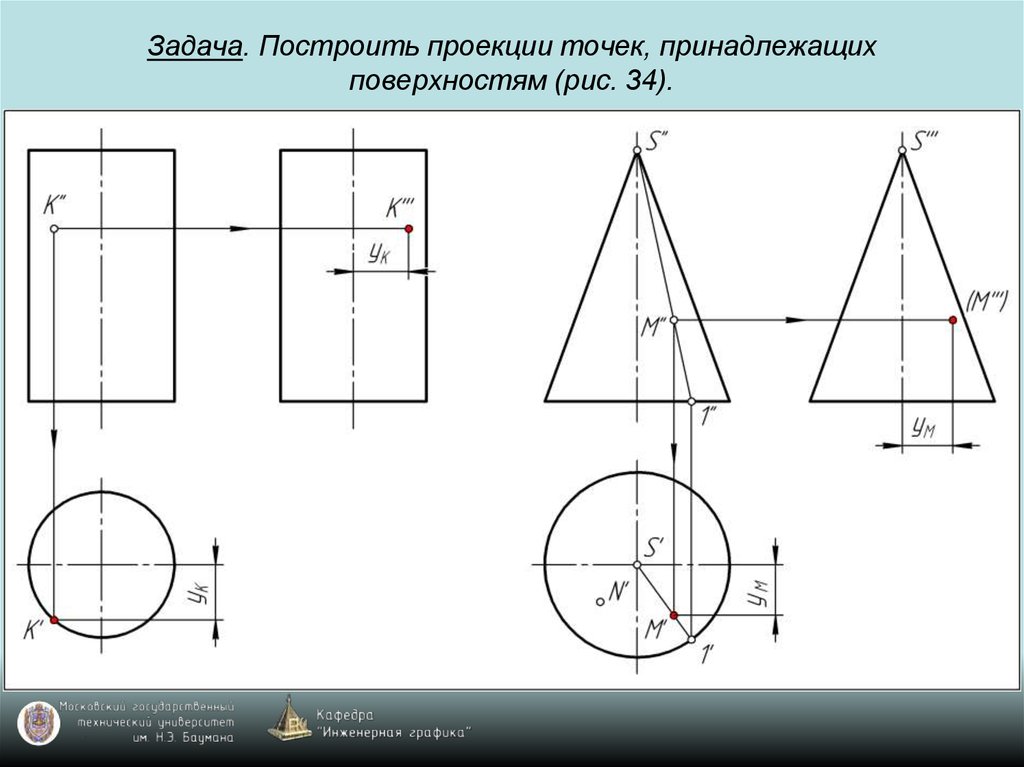
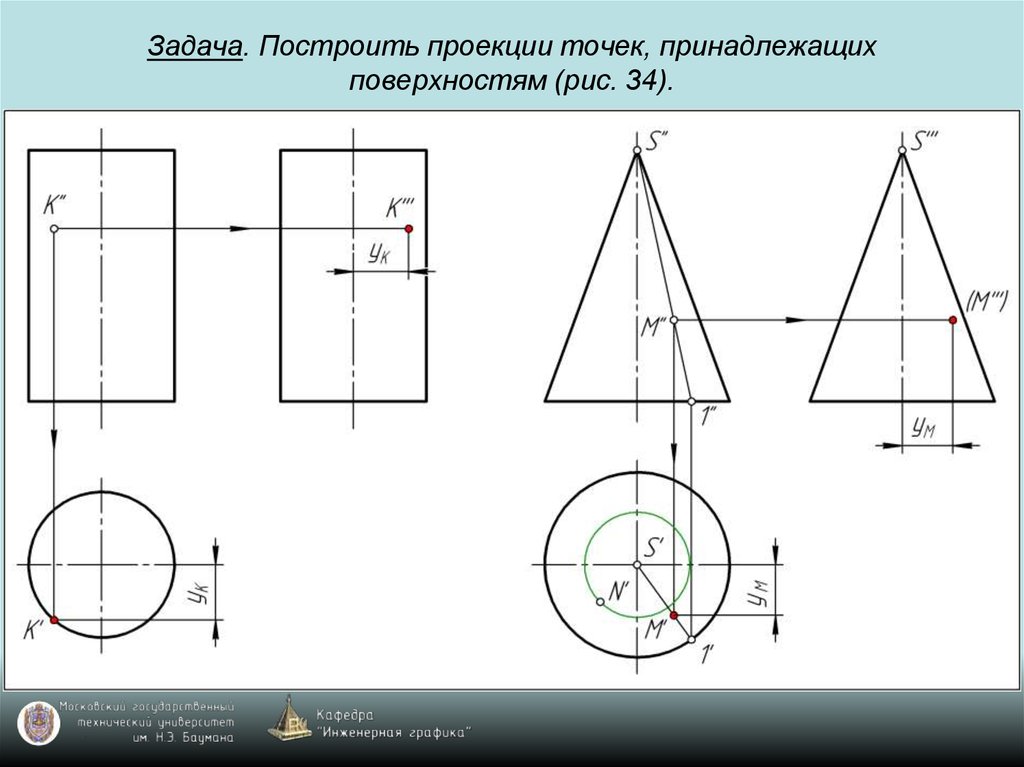
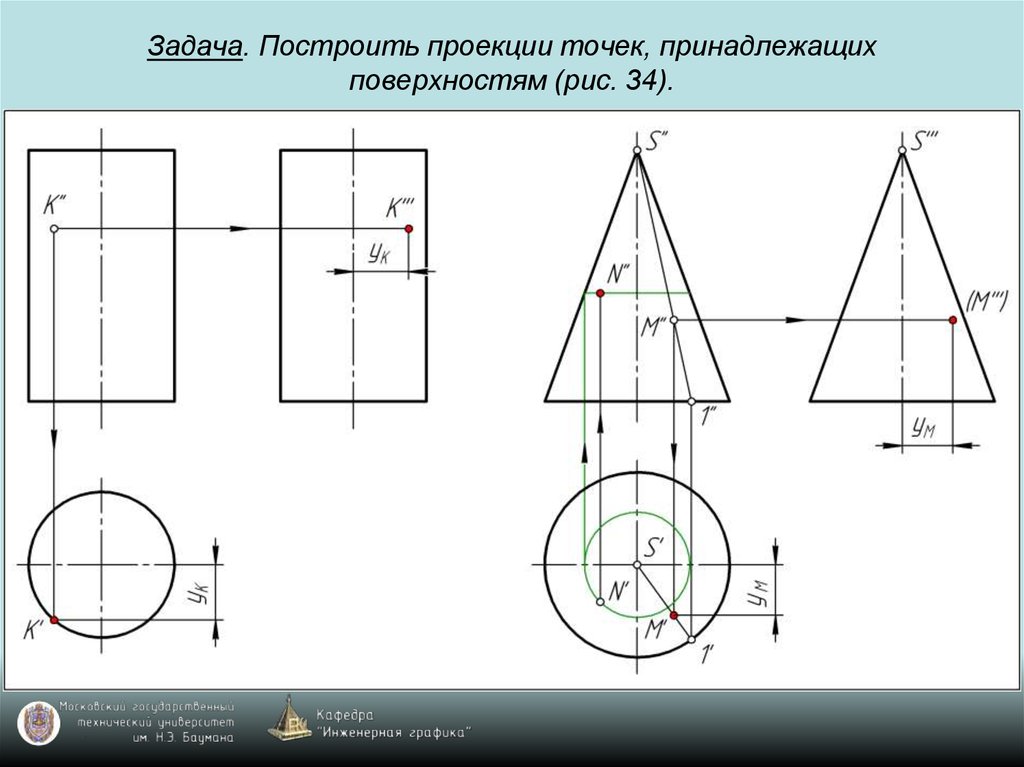
69. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).

70. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).

71. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).

72. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).

73. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).

74. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).

75. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).

76. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).

77. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).

78. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).

79. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).

80. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).

81. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).

82. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).

83. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).

84. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).

85. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).

86. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).

87. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).

88. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).

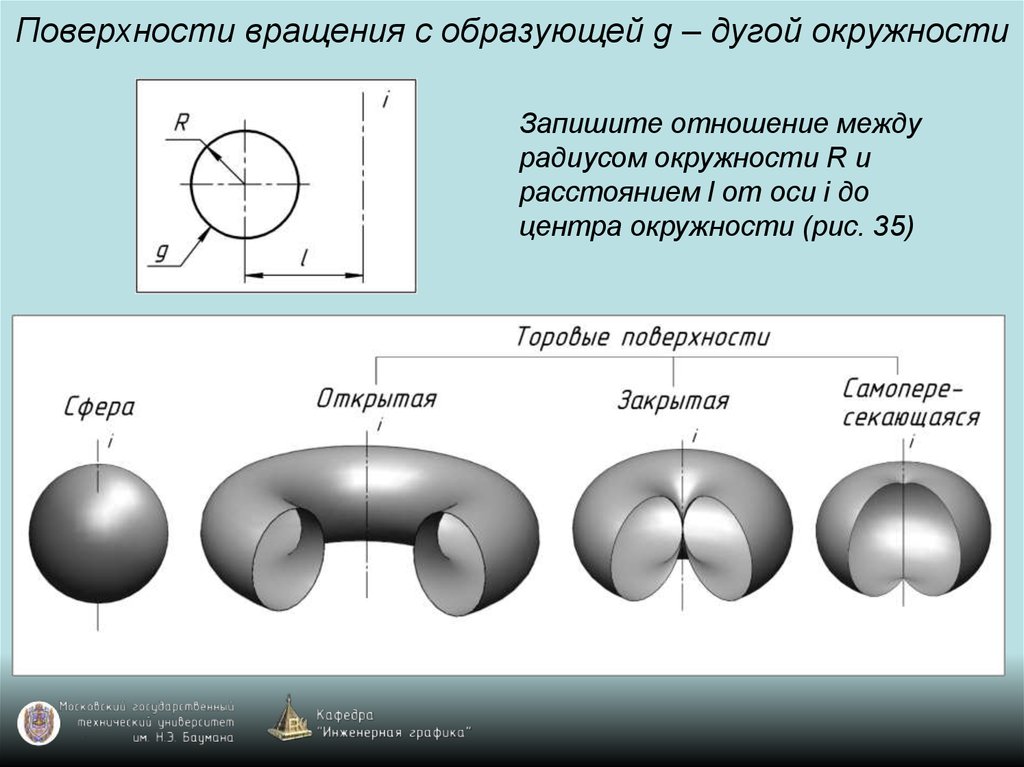
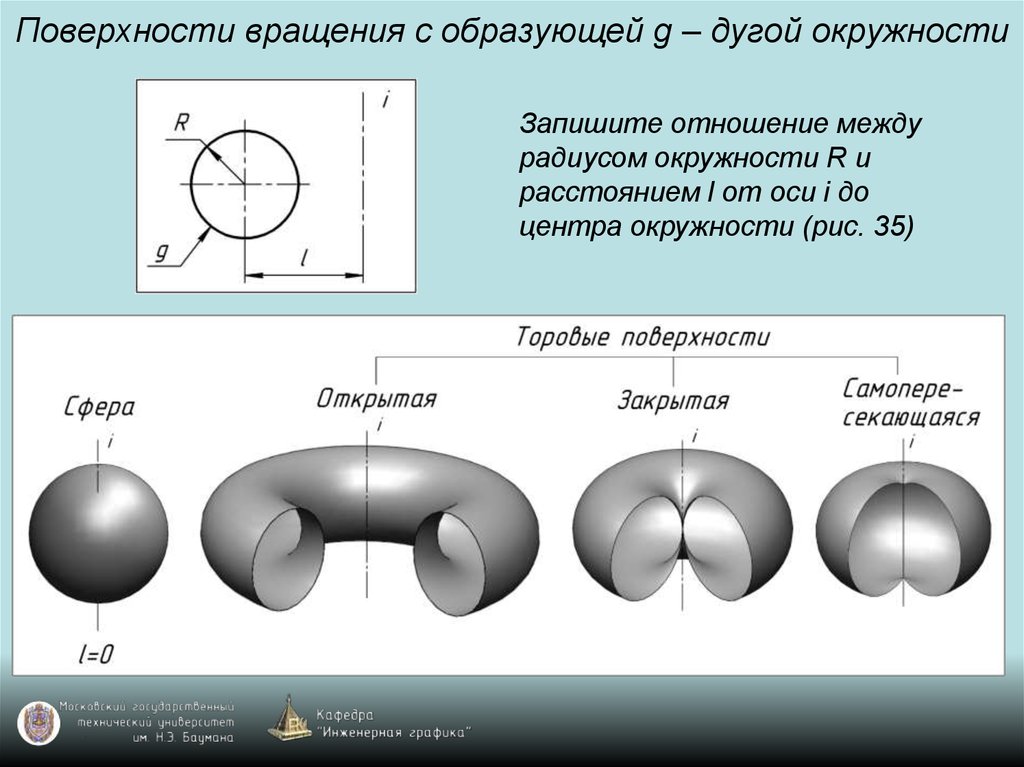
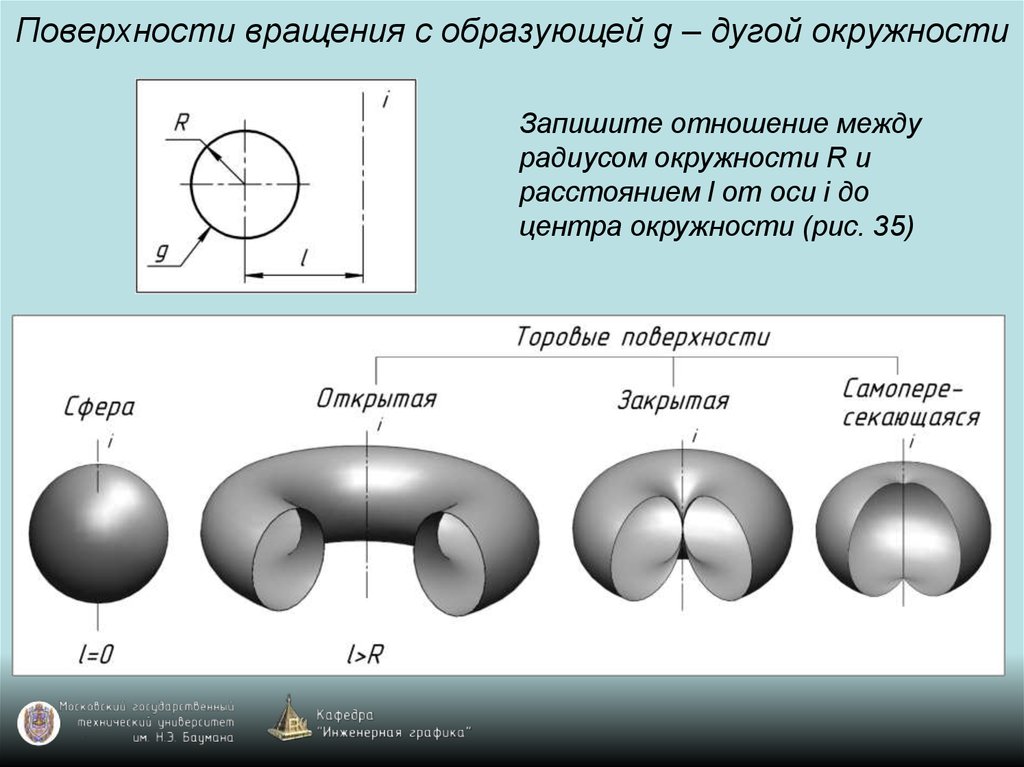
89. Поверхности вращения с образующей g – дугой окружности

Запишите отношение между
радиусом окружности R и
расстоянием l от оси i до
центра окружности (рис. 35)

90. Поверхности вращения с образующей g – дугой окружности

Запишите отношение между
радиусом окружности R и
расстоянием l от оси i до
центра окружности (рис. 35)

91. Поверхности вращения с образующей g – дугой окружности

Запишите отношение между
радиусом окружности R и
расстоянием l от оси i до
центра окружности (рис. 35)

92. Поверхности вращения с образующей g – дугой окружности

Запишите отношение между
радиусом окружности R и
расстоянием l от оси i до
центра окружности (рис. 35)

93. Поверхности вращения с образующей g – дугой окружности

Запишите отношение между
радиусом окружности R и
расстоянием l от оси i до
центра окружности (рис. 35)

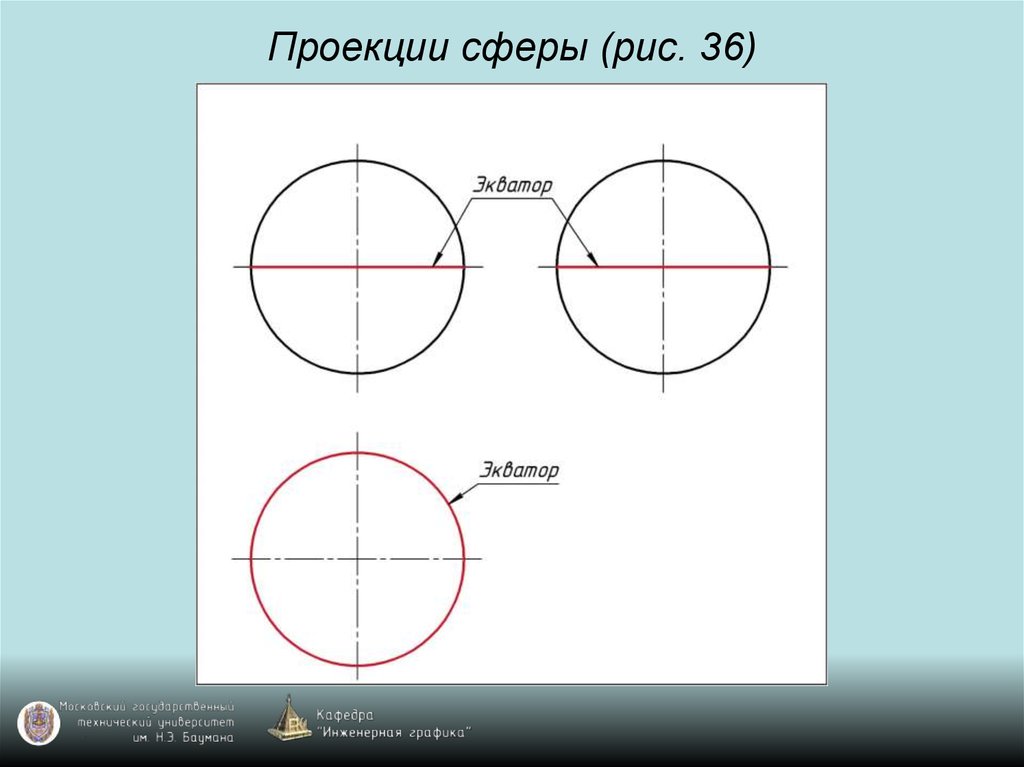
94. Проекции сферы (рис. 36)

95. Проекции сферы (рис. 36)

96. Проекции сферы (рис. 36)

97. Проекции сферы (рис. 36)

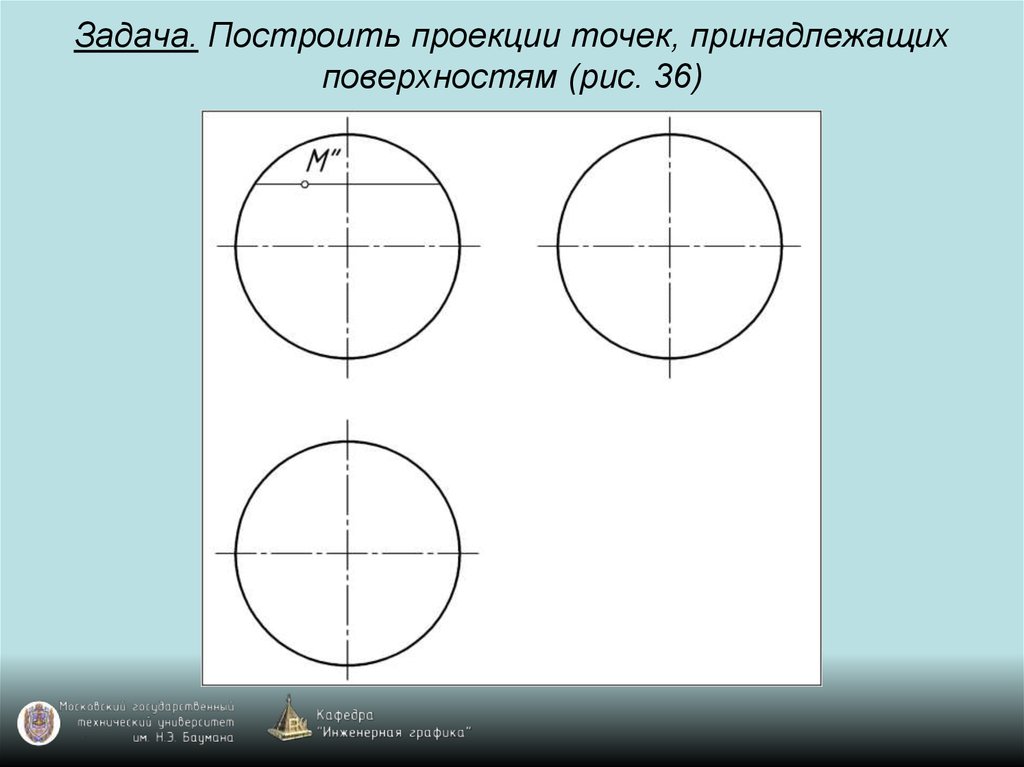
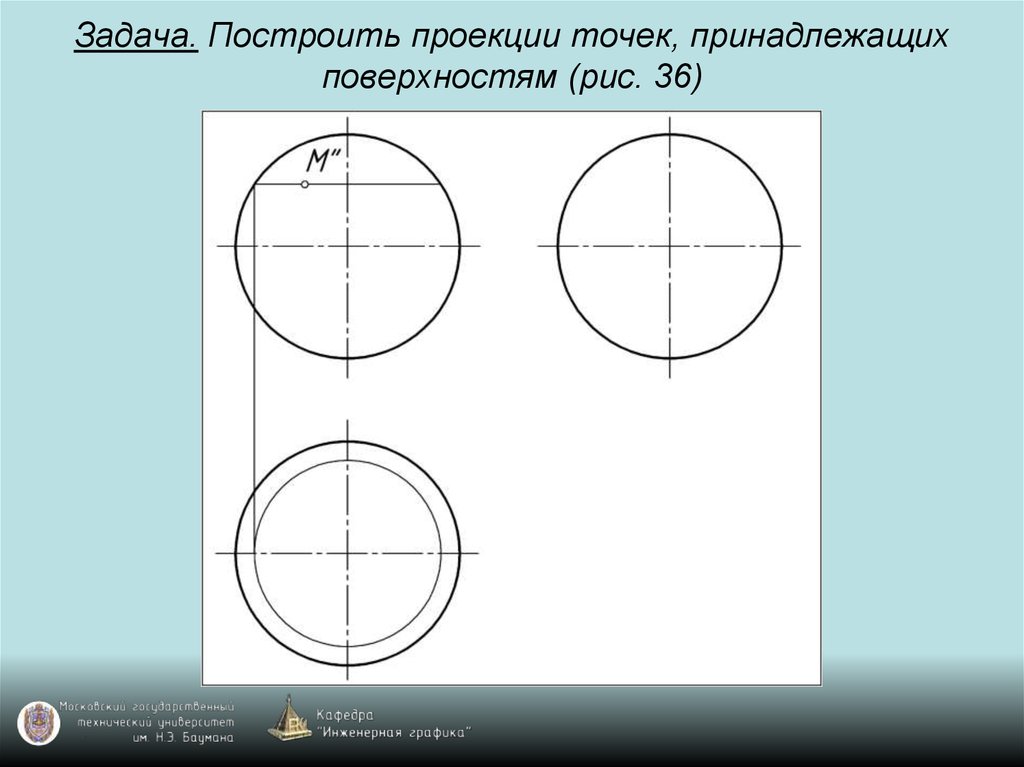
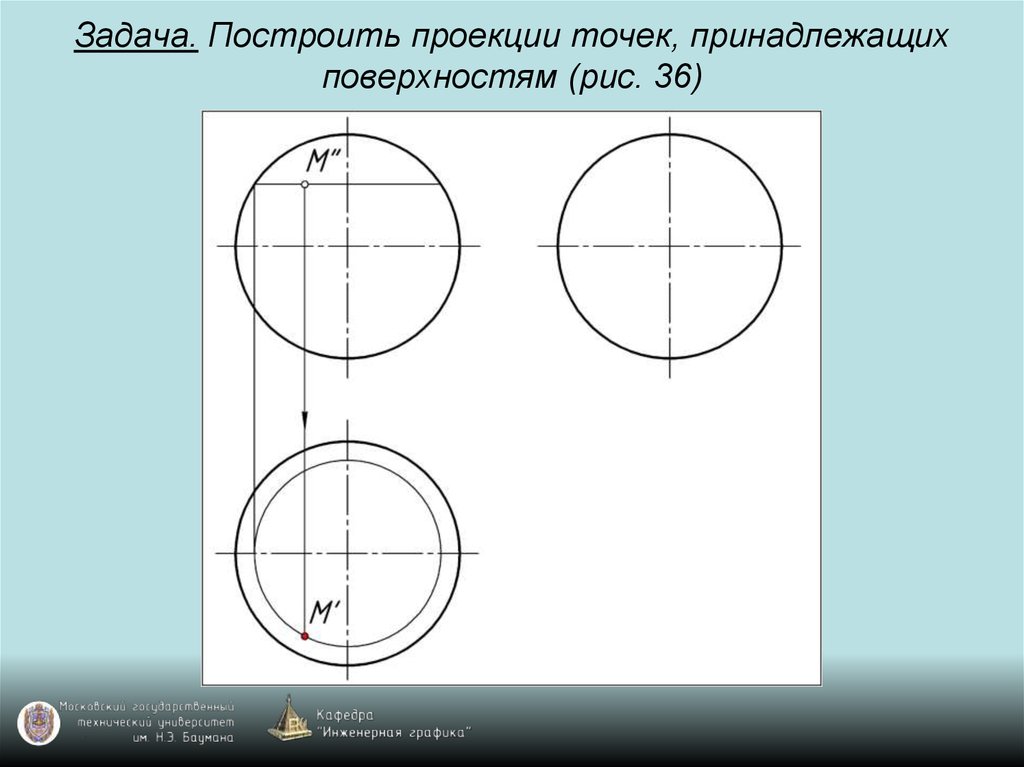
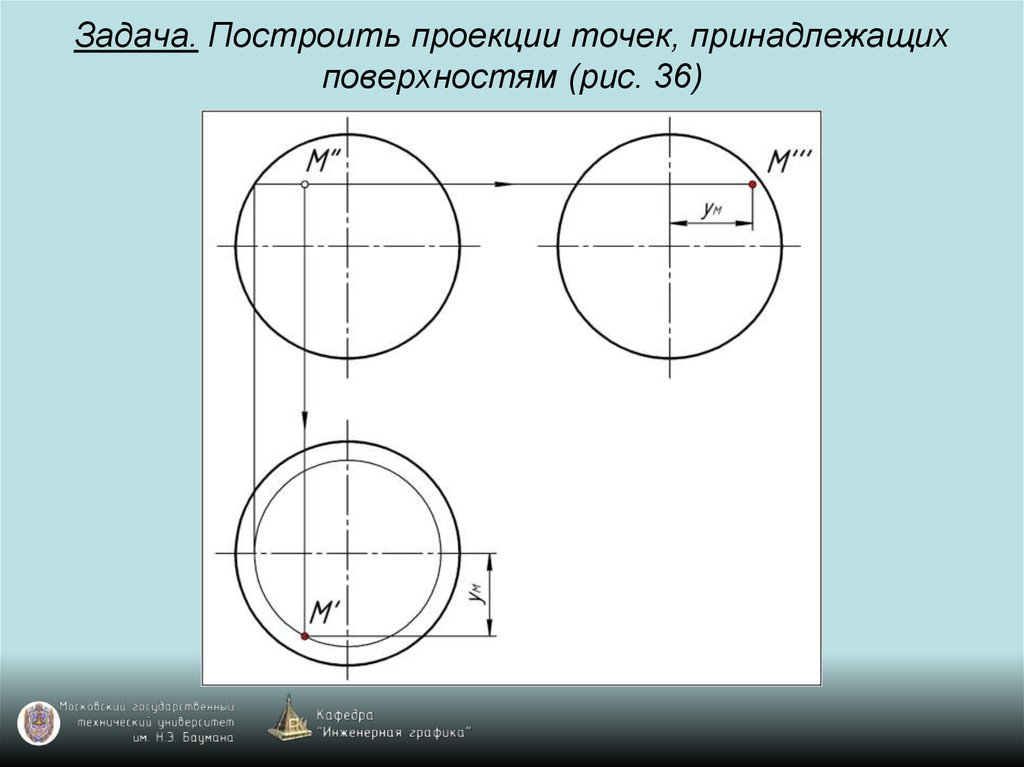
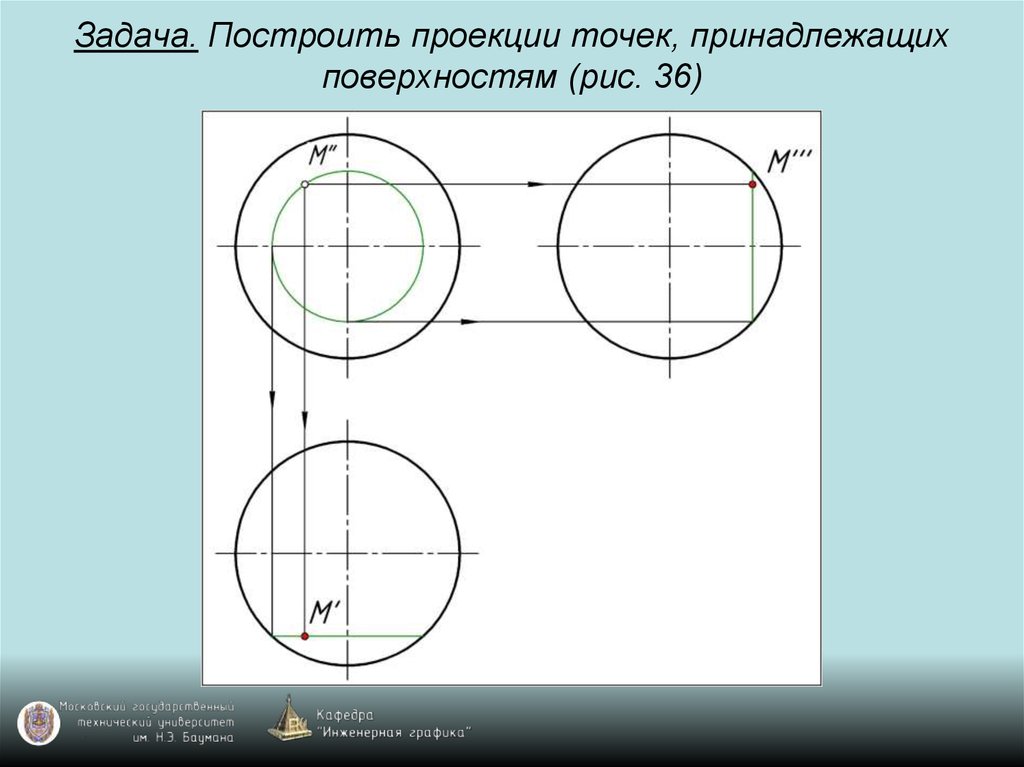
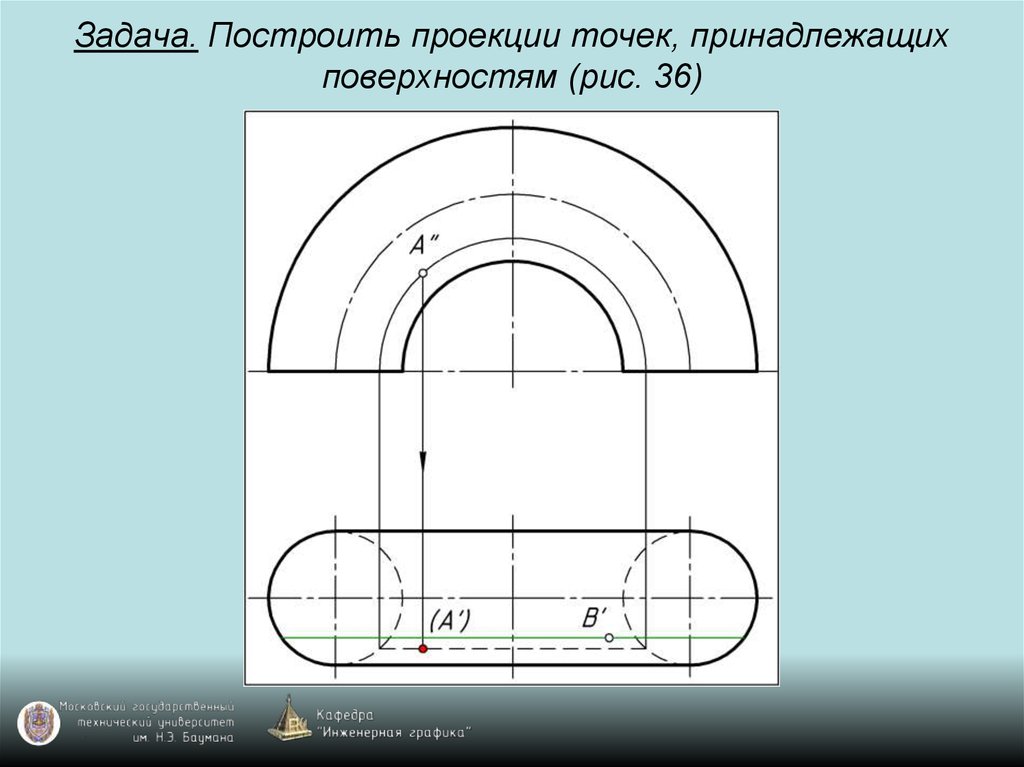
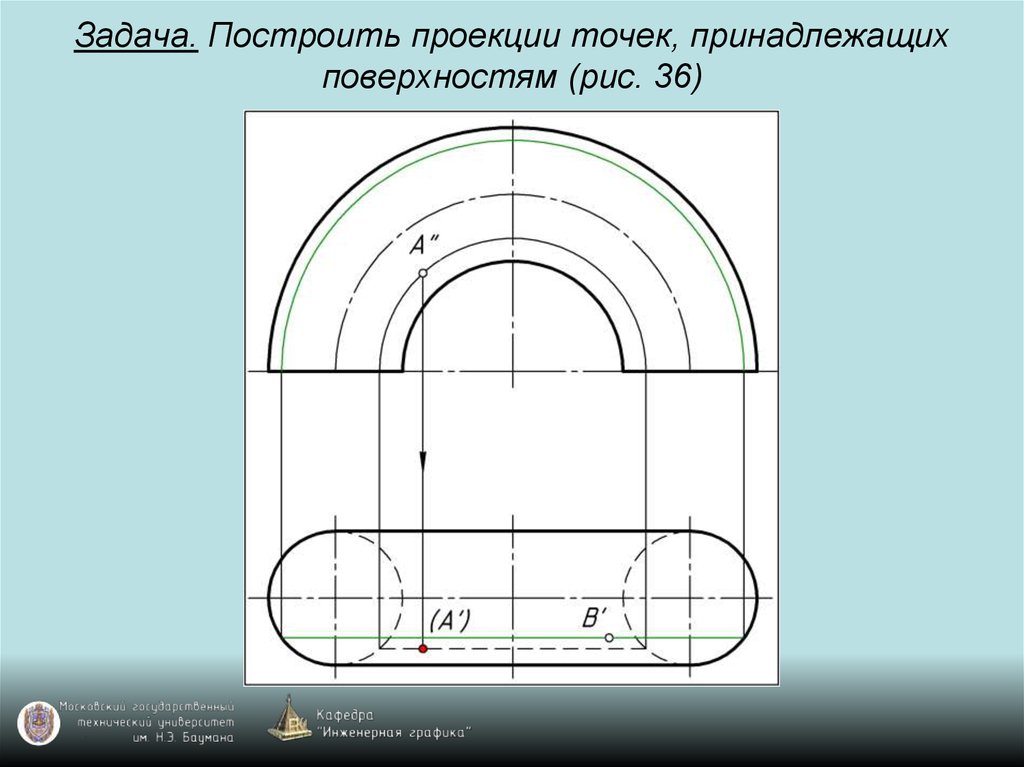
98. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)

99. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)

100. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)

101. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)

102. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)

103. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)

104. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)

105. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)

106. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)

107. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)

108. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)

109. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)

110. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)

111. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)

112. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)

113. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)

114. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)

115. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)

116. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)

117. Винтовые поверхности

Винтовая поверхность образована винтовым движением
образующей, т.е. вращением образующей вокруг оси и одновременным
перемещением вдоль оси i.
• Все точки образующей gi перемещаются по винтовым линиям.
Винтовая линия является направляющей d винтовой поверхности.
• Ход винтовой поверхности Ph.– величина линейного перемещения
точки винтовой поверхности при повороте этой точки на угол 360°
вокруг оси поверхности. Ход винтовой поверхности определяется
ходом винтовой линии
• Винтовые поверхности различают в зависимости от параметров
винтовой линии и формы образующей.

118.

• Чаще всего в технике применяют в качестве направляющей
цилиндрическую винтовую линию, называемую гелисой.
Винтовая поверхность с прямолинейной образующей
(линейчатая винтовая поверхность) с направляющей гелисой
называется геликоидом.
• Геликоиды разделяются на закрытые (g∩i), открытые (g ∙ i),
прямые (g ┴ i), наклонные (g не ┴ i).

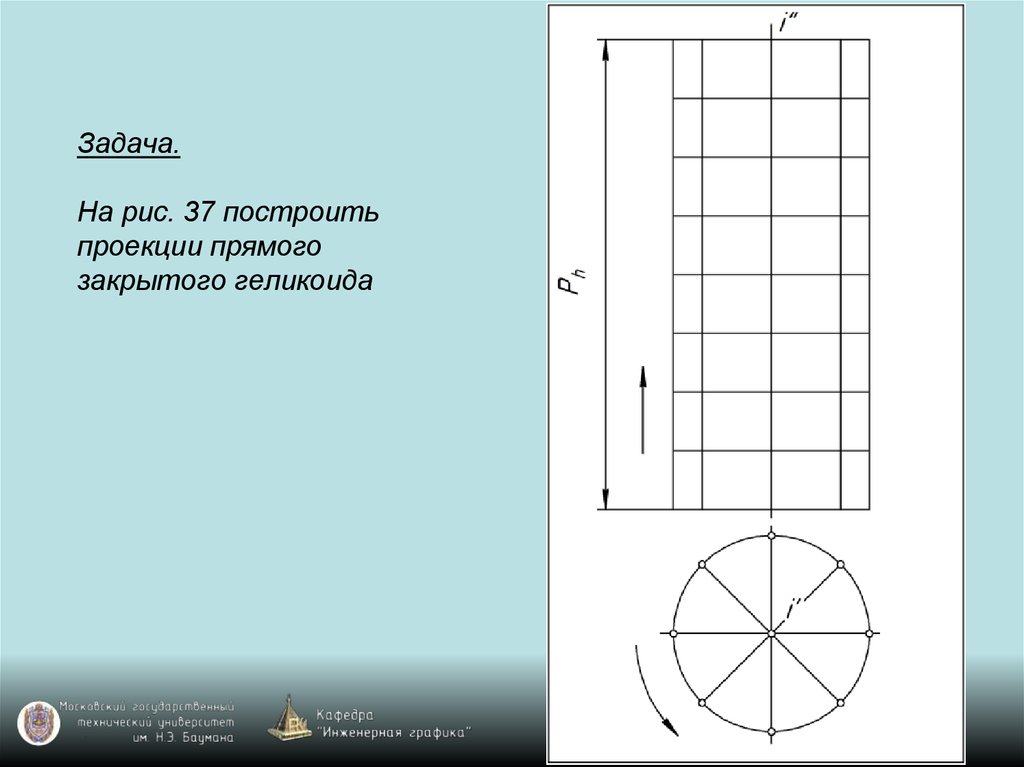
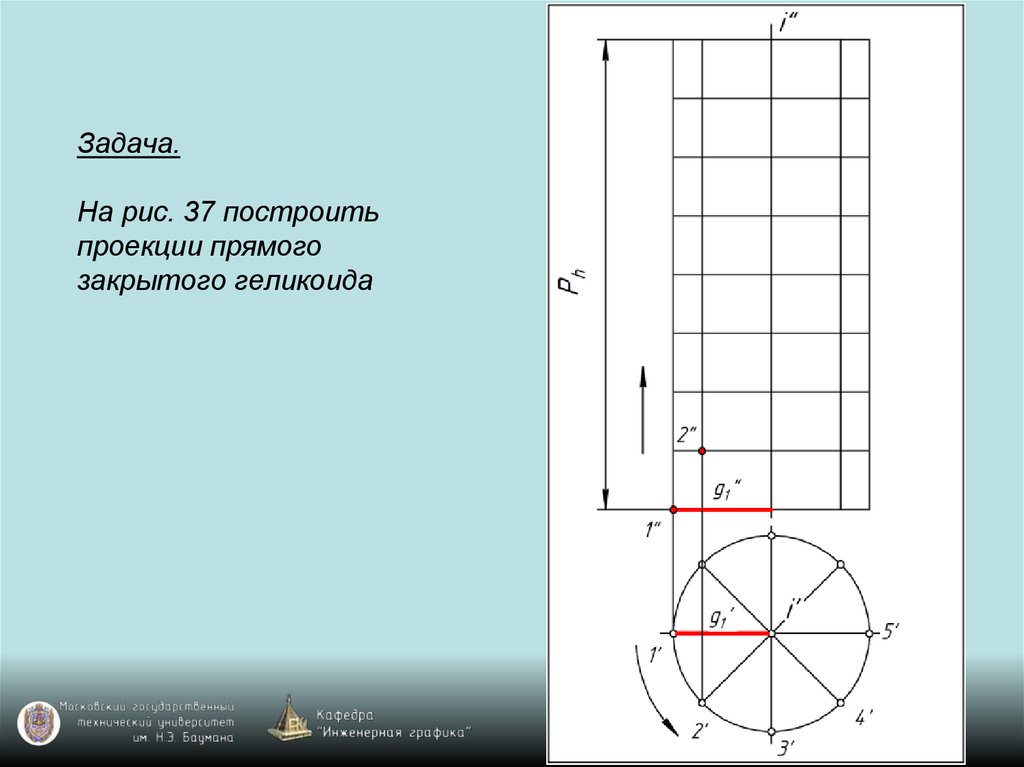
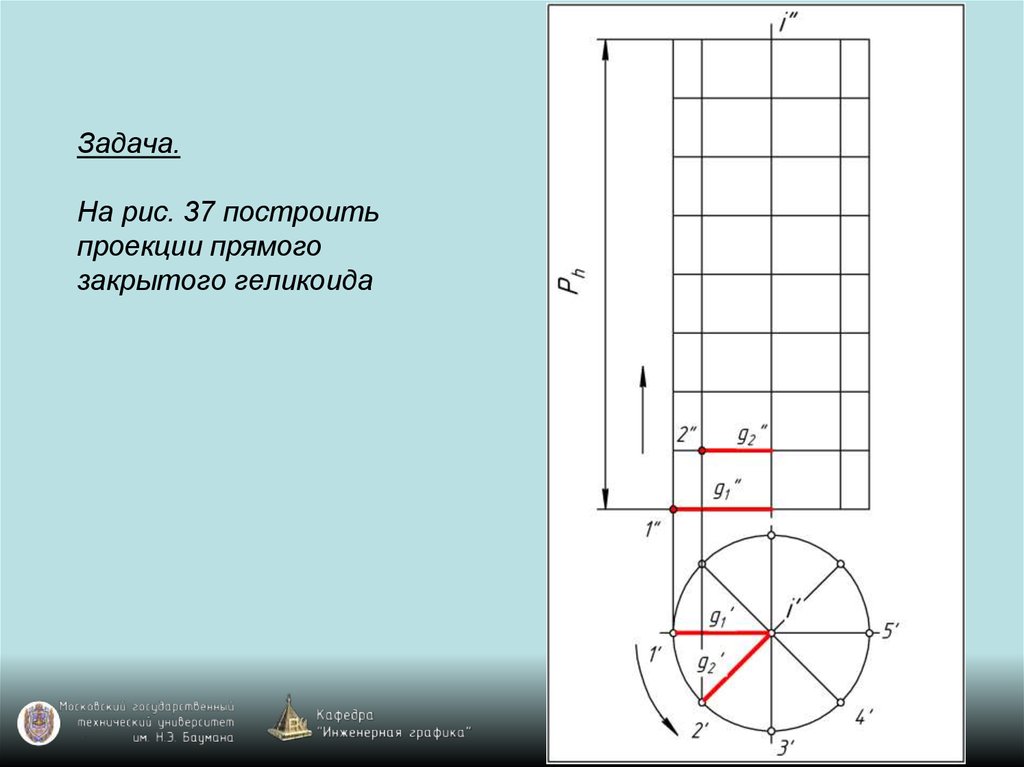
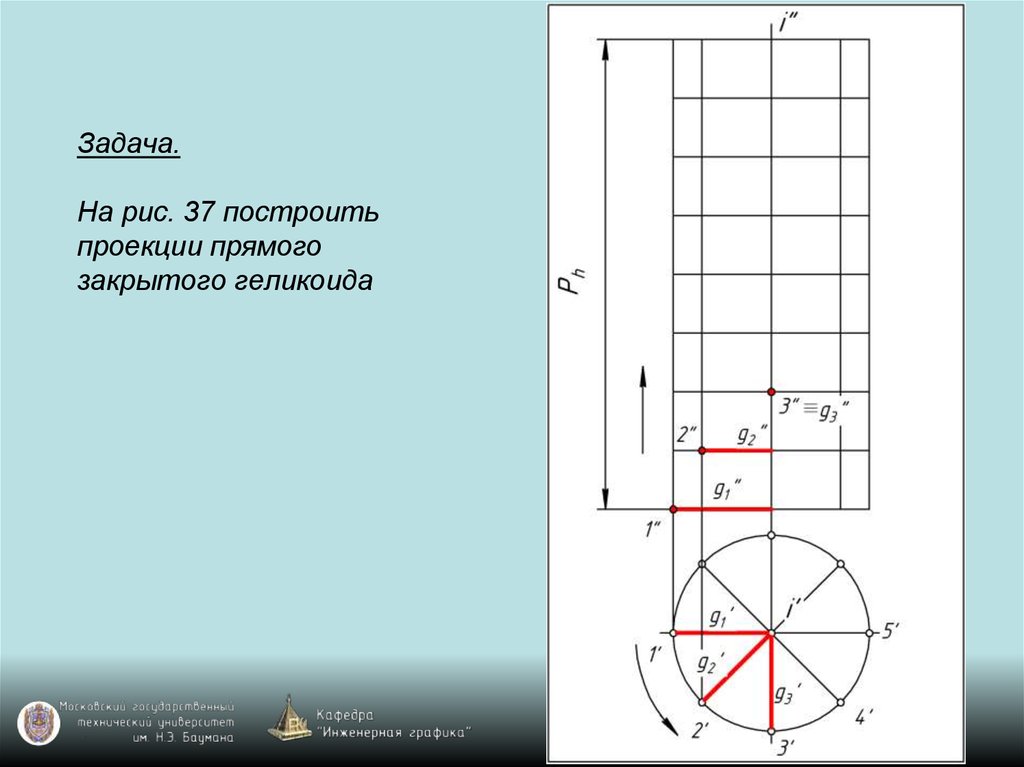
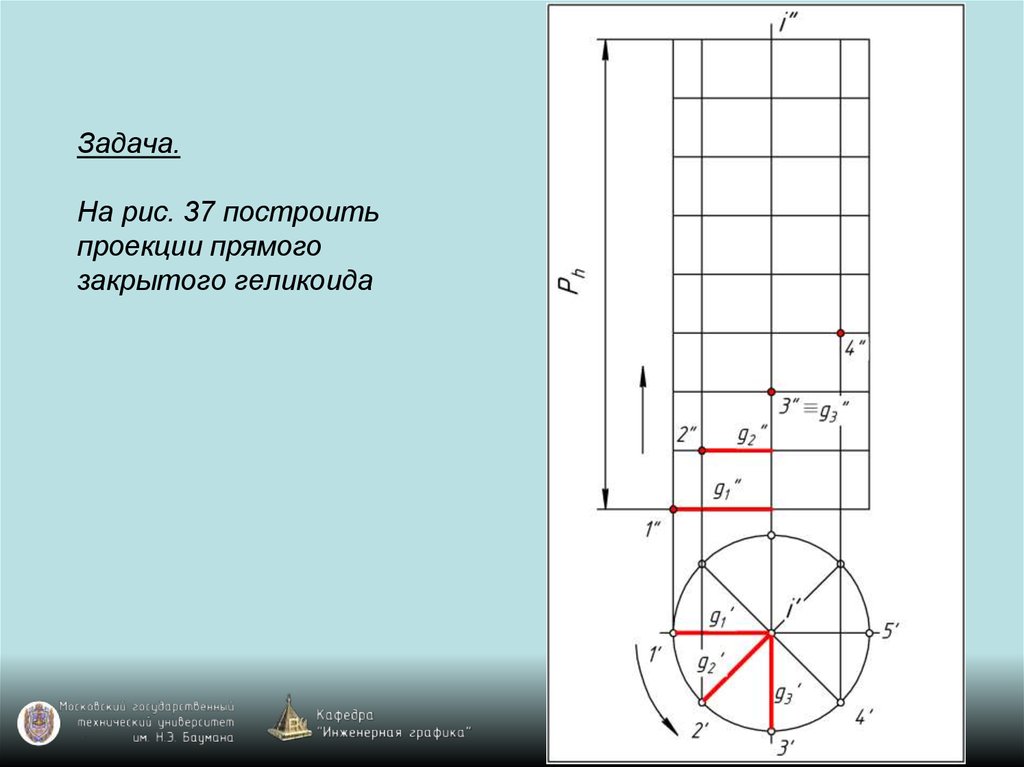
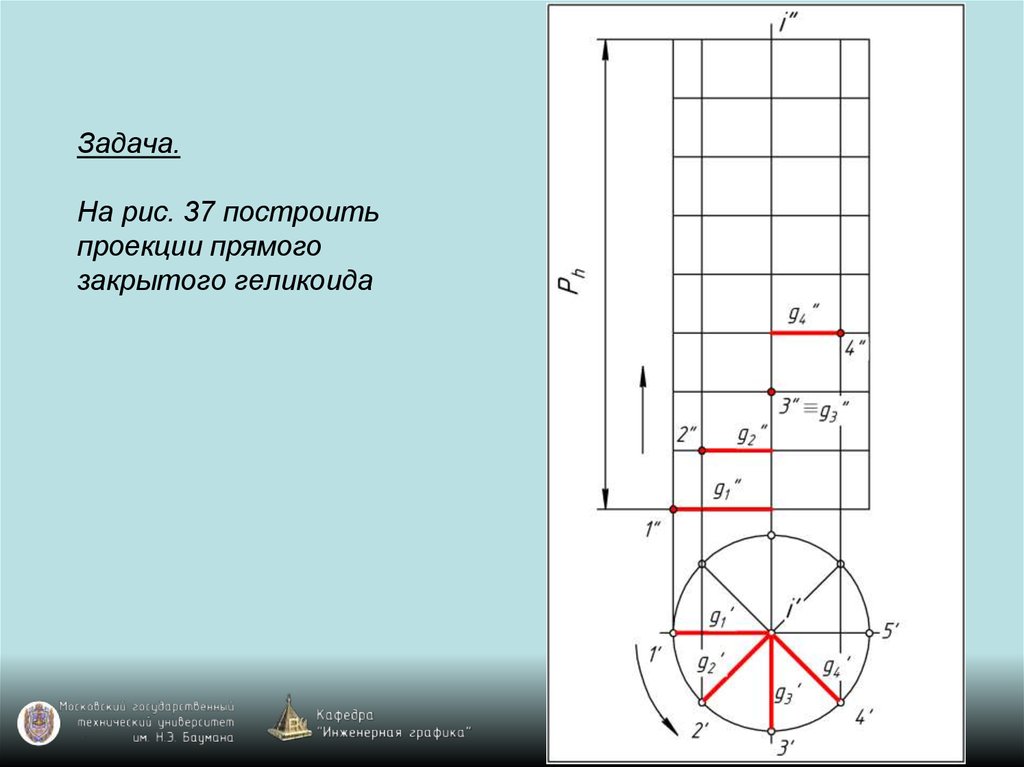
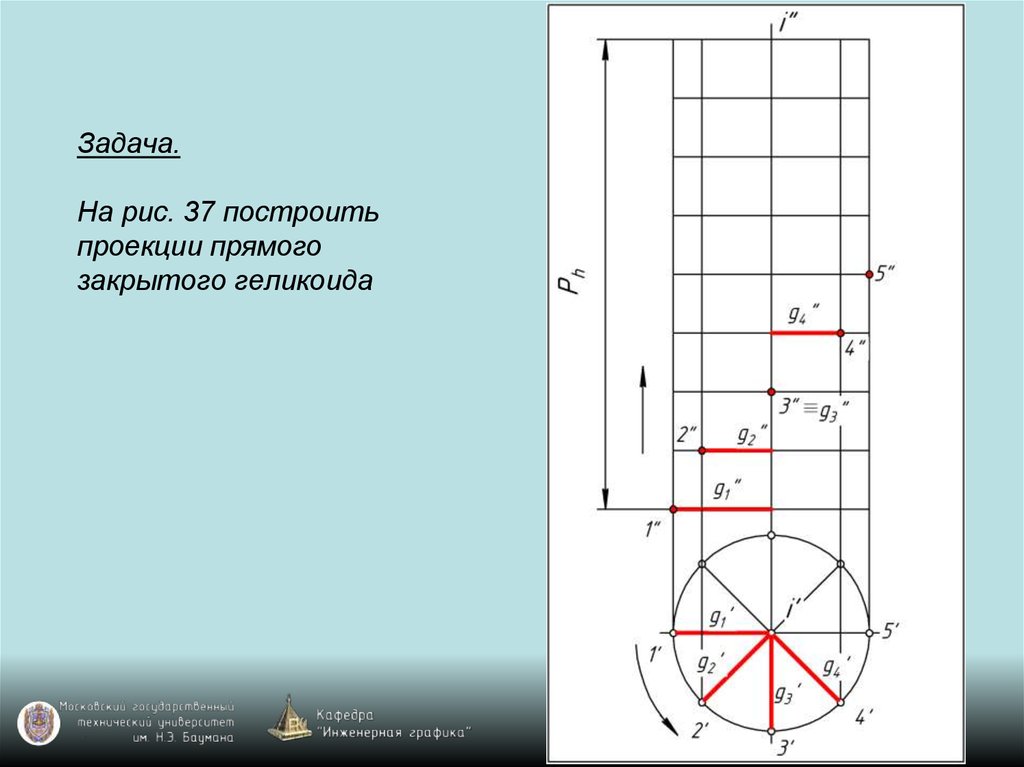
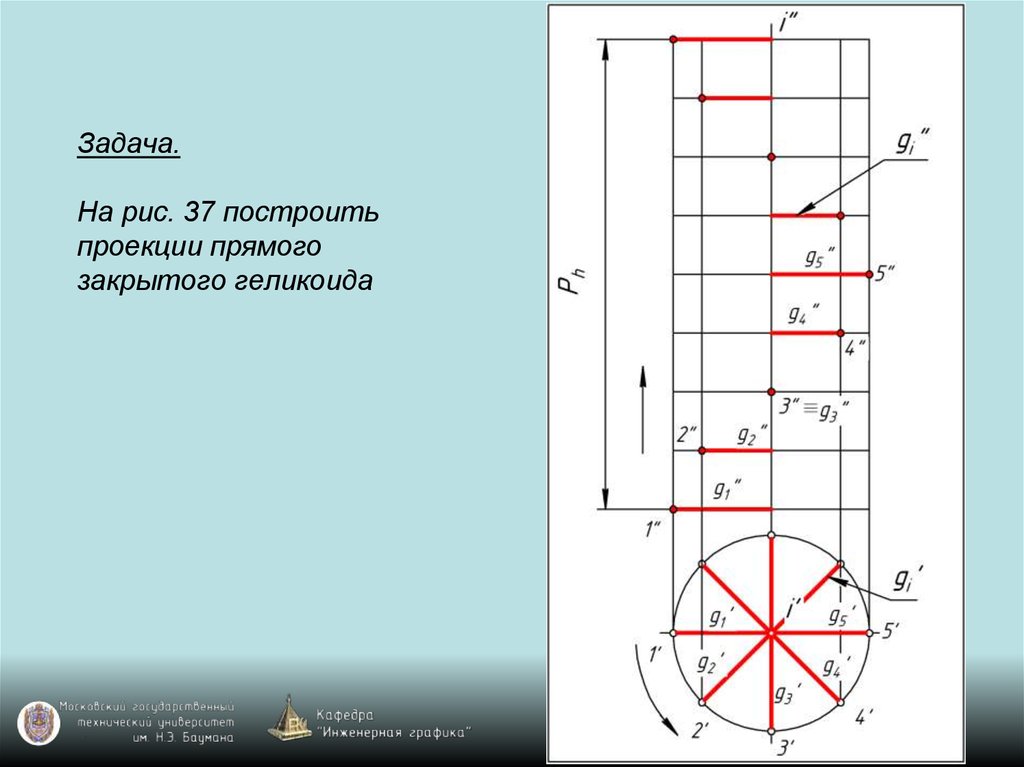
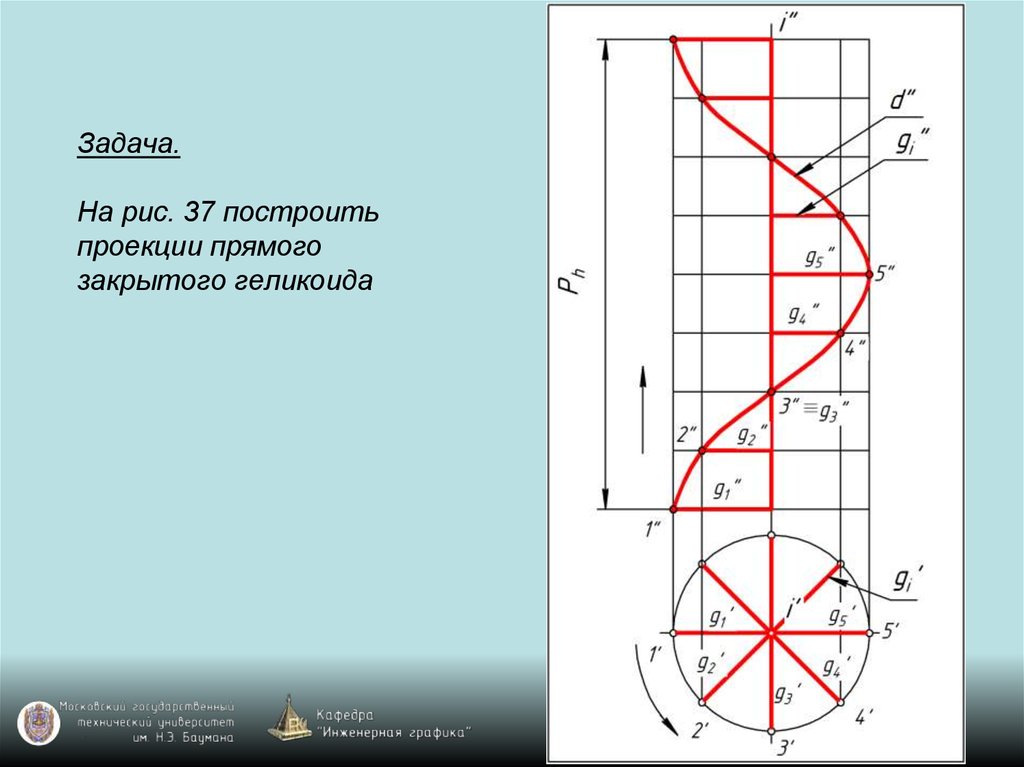
119. Задача. На рис. 37 построить проекции прямого закрытого геликоида

120. Задача. На рис. 37 построить проекции прямого закрытого геликоида

121. Задача. На рис. 37 построить проекции прямого закрытого геликоида

122. Задача. На рис. 37 построить проекции прямого закрытого геликоида

123. Задача. На рис. 37 построить проекции прямого закрытого геликоида

124. Задача. На рис. 37 построить проекции прямого закрытого геликоида

125. Задача. На рис. 37 построить проекции прямого закрытого геликоида

126. Задача. На рис. 37 построить проекции прямого закрытого геликоида

127. Задача. На рис. 37 построить проекции прямого закрытого геликоида

128. Задача. На рис. 37 построить проекции прямого закрытого геликоида

129. Задача. На рис. 37 построить проекции прямого закрытого геликоида

130. Задача. На рис. 37 построить проекции прямого закрытого геликоида

131. Задача. На рис. 37 построить проекции прямого закрытого геликоида

132. Задача. На рис. 37 построить проекции прямого закрытого геликоида

133. Задача. На рис. 37 построить проекции прямого закрытого геликоида

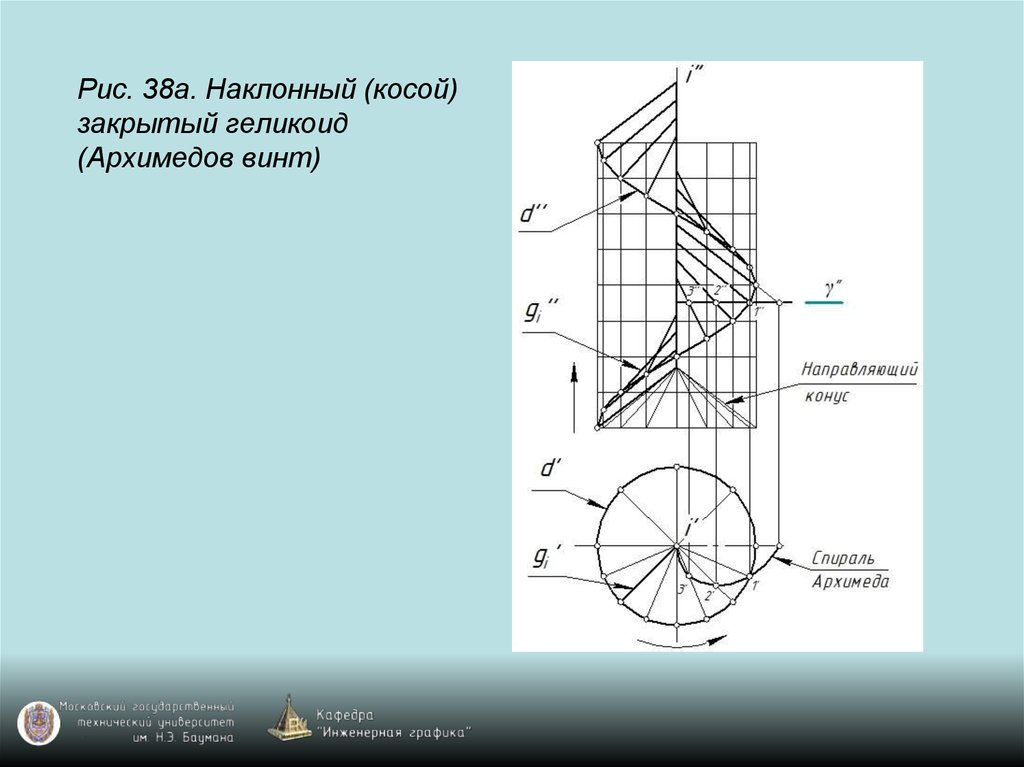
134. Рис. 38а. Наклонный (косой) закрытый геликоид (Архимедов винт)

135.

Рис. 38б. Прямой
открытый геликоид