Похожие презентации:
Квадратичная функция у = ах + bх + с
1. Квадратичная функция у = ах + bх + с
22.
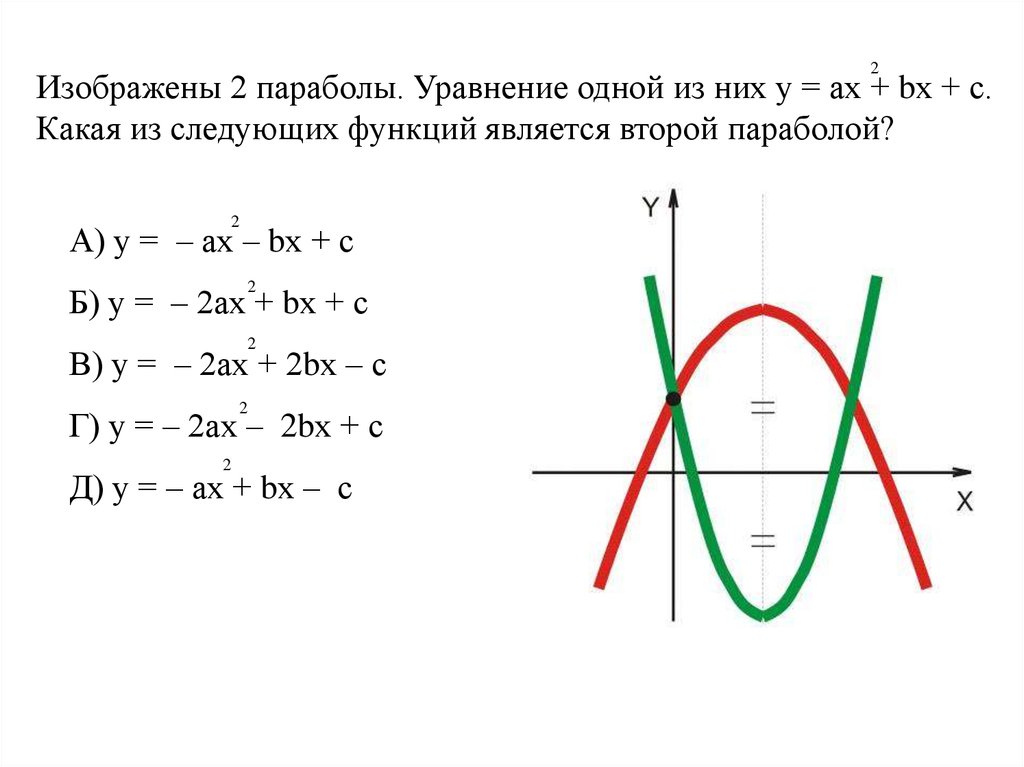
2Изображены 2 параболы. Уравнение одной из них у = ах + bх + с.
Какая из следующих функций является второй параболой?
2
А) у = – ах – bх + с
2
Б) у = – 2ах + bх + с
2
В) у = – 2ах + 2bх – с
2
Г) у = – 2ах – 2bх + с
2
Д) у = – ах + bх – с
3.
№1. Найти значения х, при которых значения функцииу положительны.
Y
А
Б
В
X
(-∞; 1) U (3; ∞)
(0; 4)
(-∞; -2) U (-2; ∞)
4.
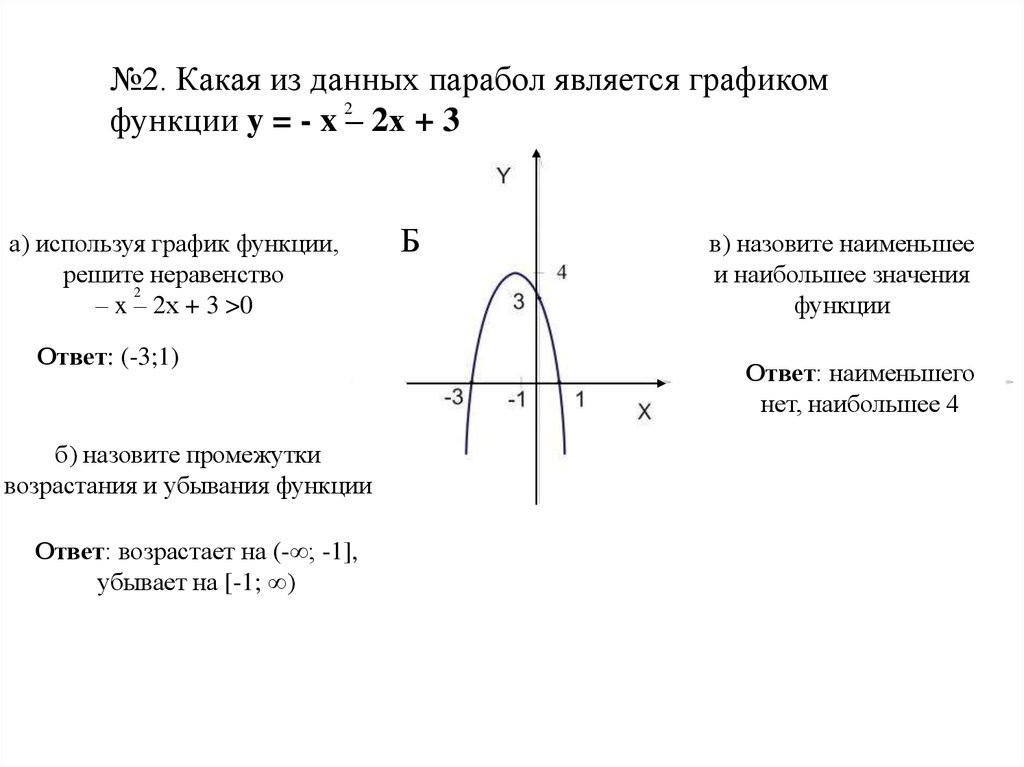
№2. Какая из данных парабол является графикомфункции y = - x 2– 2х + 3
а) используя
А график функции,
решите неравенство
2
– x – 2х + 3 >0
Ответ: (-3;1)
б) назовите промежутки
возрастания и убывания функции
Ответ: возрастает на (-∞; -1],
убывает на [-1; ∞)
Б
Вв) назовите наименьшее
и наибольшее значения
функции
Ответ: наименьшего
нет, наибольшее 4
5.
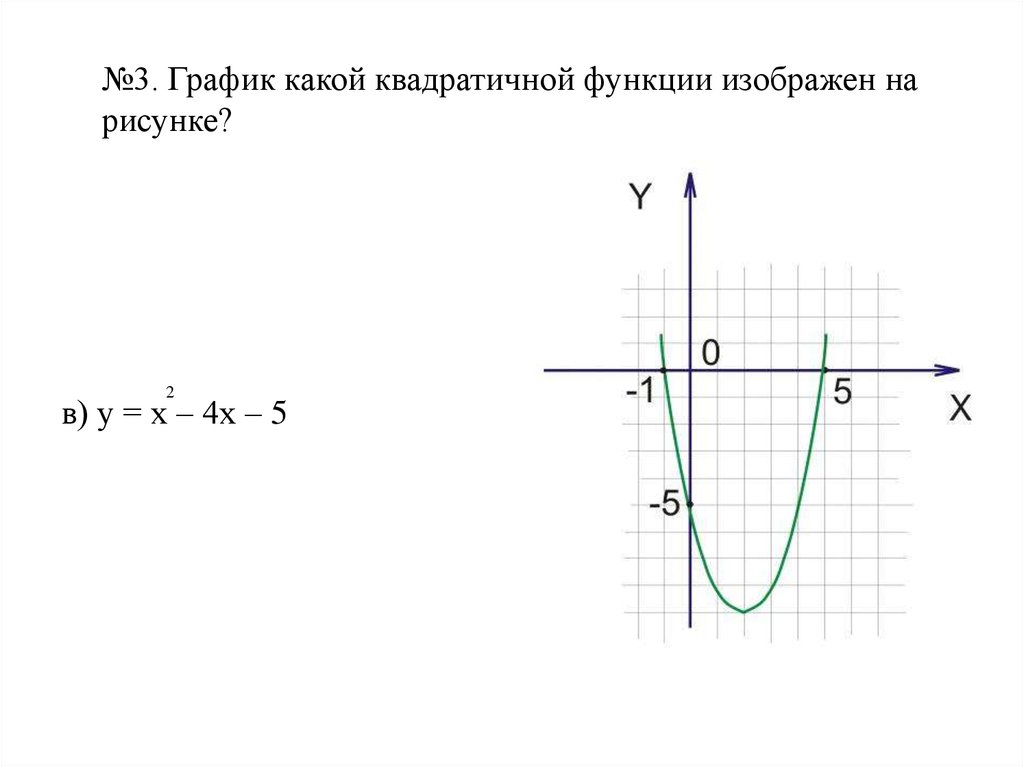
№3. График какой квадратичной функции изображен нарисунке?
2
а) у = х + 4х – 5
2
б) у = х + 6х + 5
2
в) у = х – 4х – 5
2
г) у = х – 4х + 5
6.
Тест2
1. Найти координаты вершины параболы: у = – 2х + 8х – 13
а) (-2; 5) б) (2; 5) в) (2; 7) г) (2; -5)
2. Укажите среди изображенных на рисунке
2
парабол график функции у = – х + 4х – 3
3. Запишите функцию, график которой получен из
2
параболы у = х с помощью следующей цепочки преобразований
1) сжатие в 2 раза к оси абсцисс; 2) сдвиг вправо на 3 единицы;
3) сдвиг вверх на 5 единиц
2
2
2
а) у = (0, 5х – 3) б) у = 0,5 (х + 3) – 5 в) у = 0,5 (х + 3) + 5
2
г) у = 0,5 (х – 3) + 5
2
4. С помощью графика функции у = х + 2х решите неравенство
2
х + 2х >0
а) (-∞; 0) б) (-∞; 2) U [0; ∞) в) (-2; 0) г) (-2; ∞)
2
5. При каких значениях а парабола у = ах – 2х + 25 касается оси абсцисс?
а) а = 25 б) 0 в) 0,04 г) 0,4
6. Имеет ли корни уравнение:
2
1234 х – 4231х + 2431 = 0
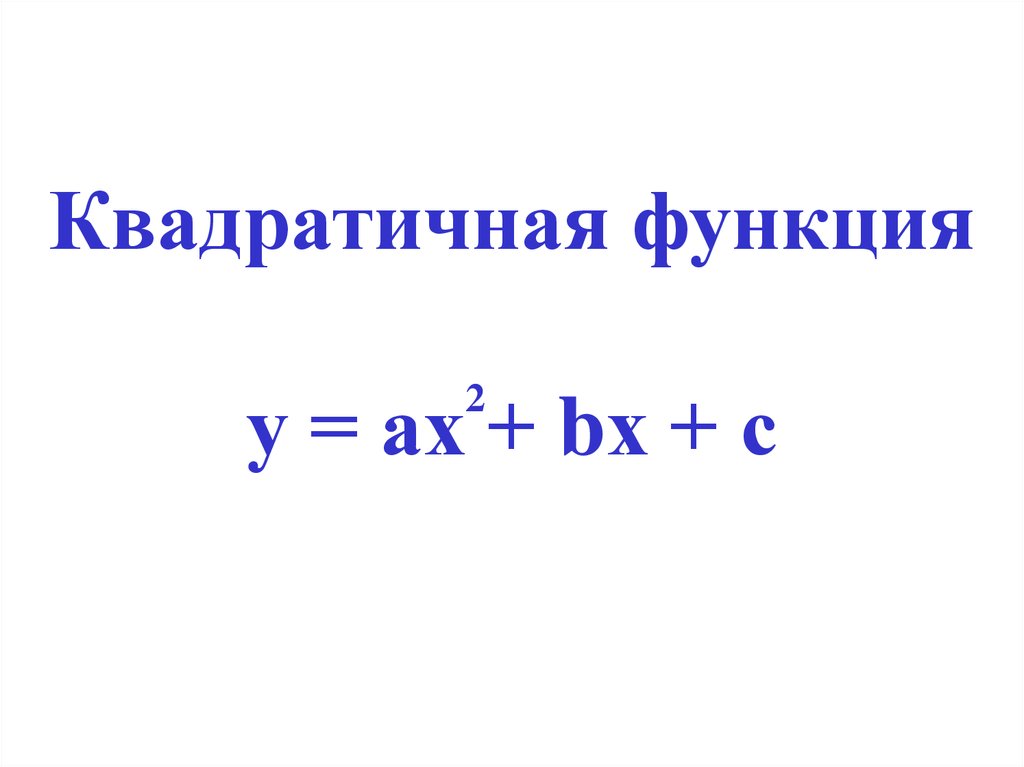


 Математика
Математика








