Симметрия. Виды симметрии

1.

Подготовил:
учитель математики
МОУСОШ №8 им.А.Я.Тимова
пос. Прикубанского
Абакумова Ю.В.

2.

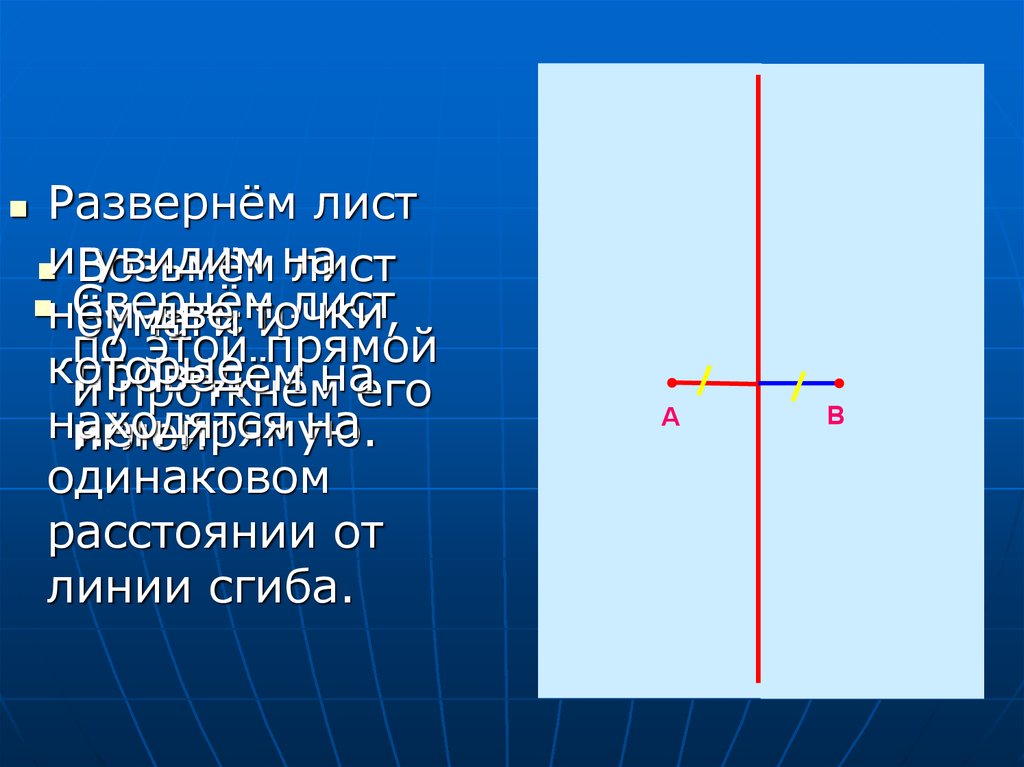
Развернём лист
увидим на
иВозьмём
лист
нём
Свернём
две точки,
бумаги
и лист
по
этой
прямой
которые
проведём
и
проткнёмнаего
находятся
на
нём прямую.
иглой.
одинаковом
расстоянии от
линии сгиба.
А
В

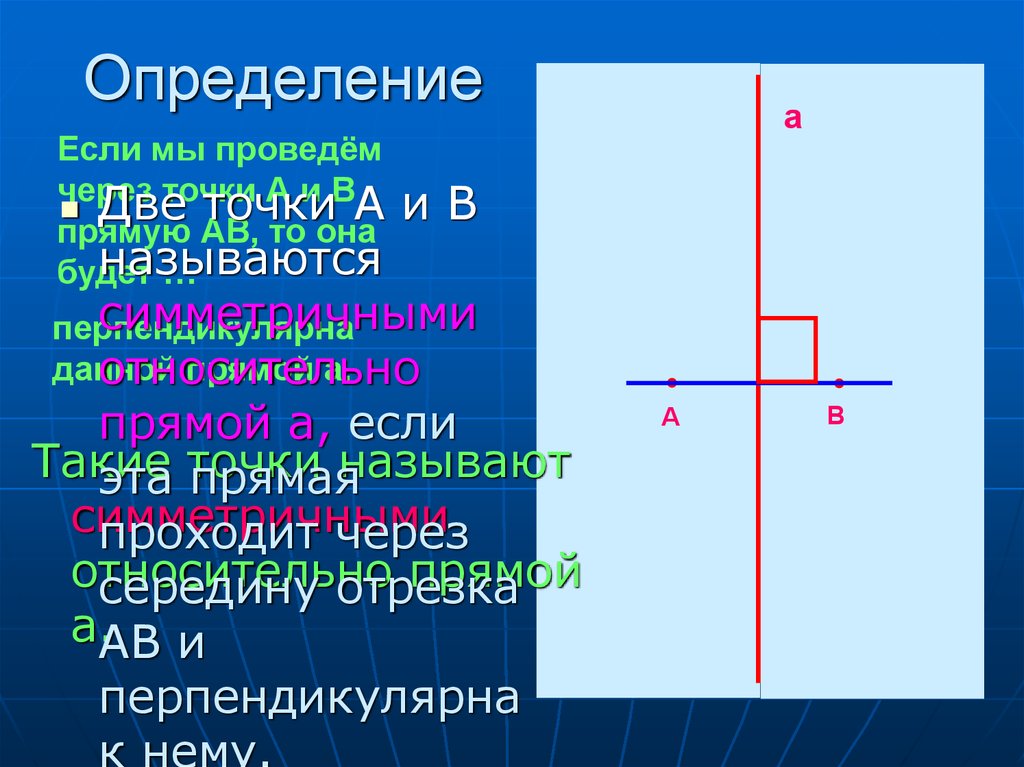
3. Определение

Если мы проведём
через точки А и В
Две точки А
прямую АВ, то она
называются
будет
…
а
иВ
симметричными
перпендикулярна
данной
прямой а.
относительно
прямой а, если
Такие
называют
эта точки
прямая
симметричными
проходит через
относительно
прямой
середину отрезка
а.АВ и
перпендикулярна
к нему.
А
В

4.

Фигура
называется
Симметричной
относительно прямой а
если для каждой точки фигуры
симметричная ей точка так же
принадлежит этой фигуре.
Прямая а называется
ось симметрии

5.

6.

Симметрия – это гармония…

7. осевая симметрия

Сколько
Все рассмотренные
фигуры имеют один
и тот же вид
симметрии, который
называется…
осей
симмет
рии
имеет
эта
фигура
?
осевая симметрия

8.

Осевая симметрия
ещё называется
зеркальной…
Зеркало

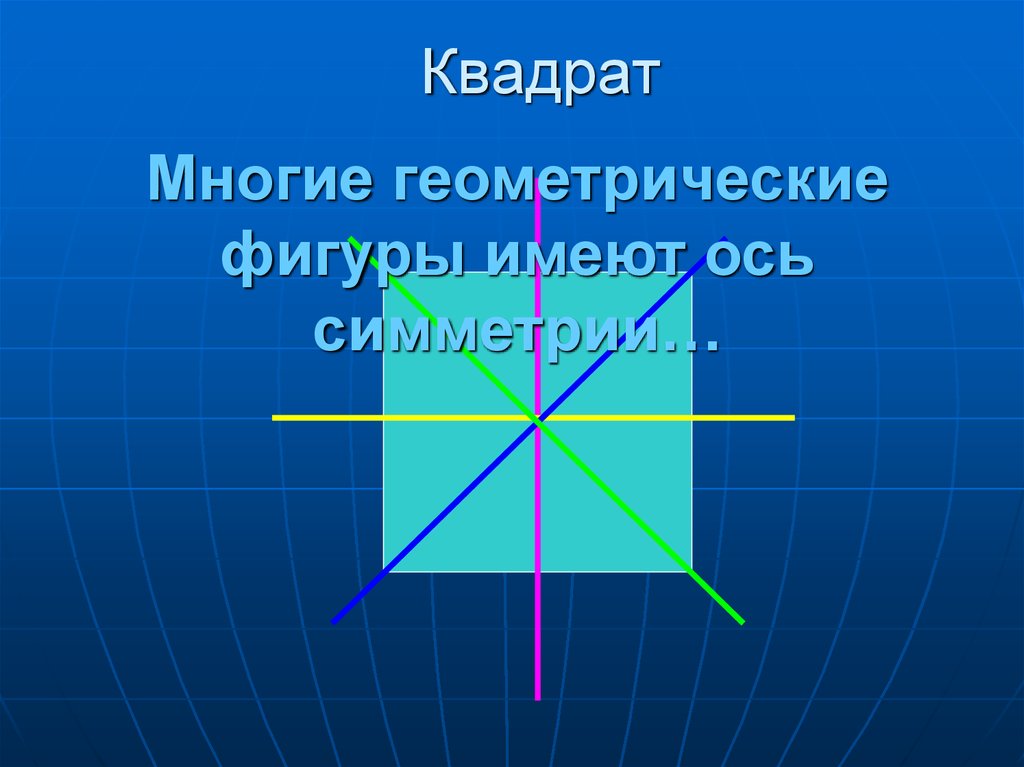
9. Квадрат

Многие геометрические
фигуры имеют ось
симметрии…

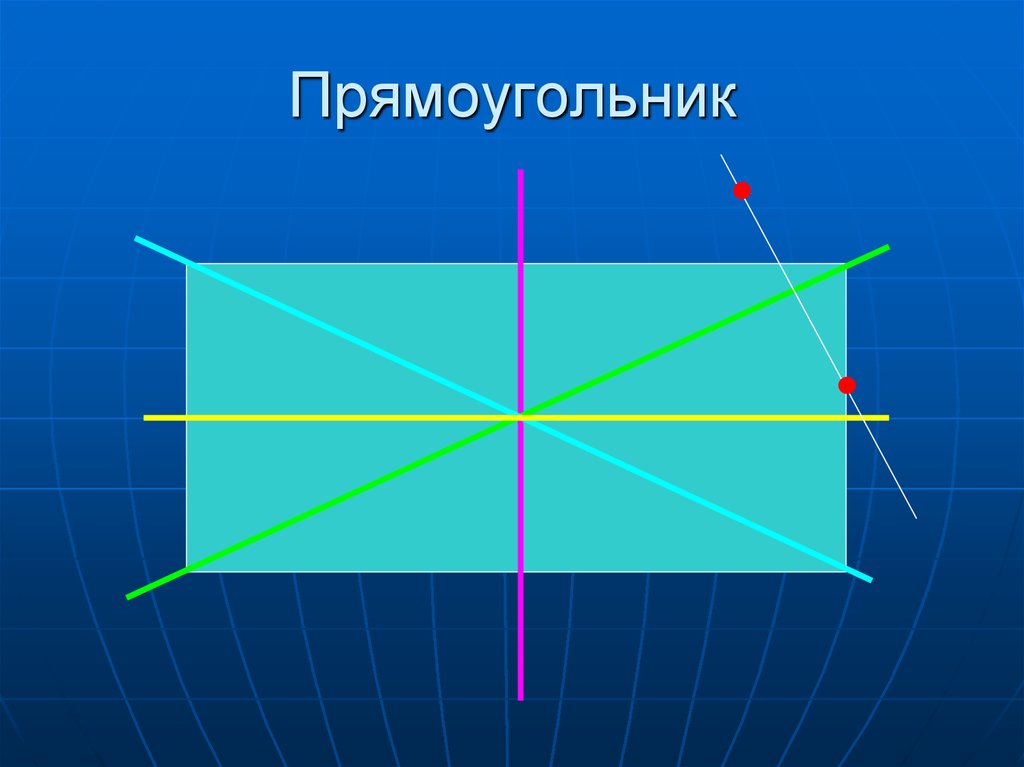
10. Прямоугольник

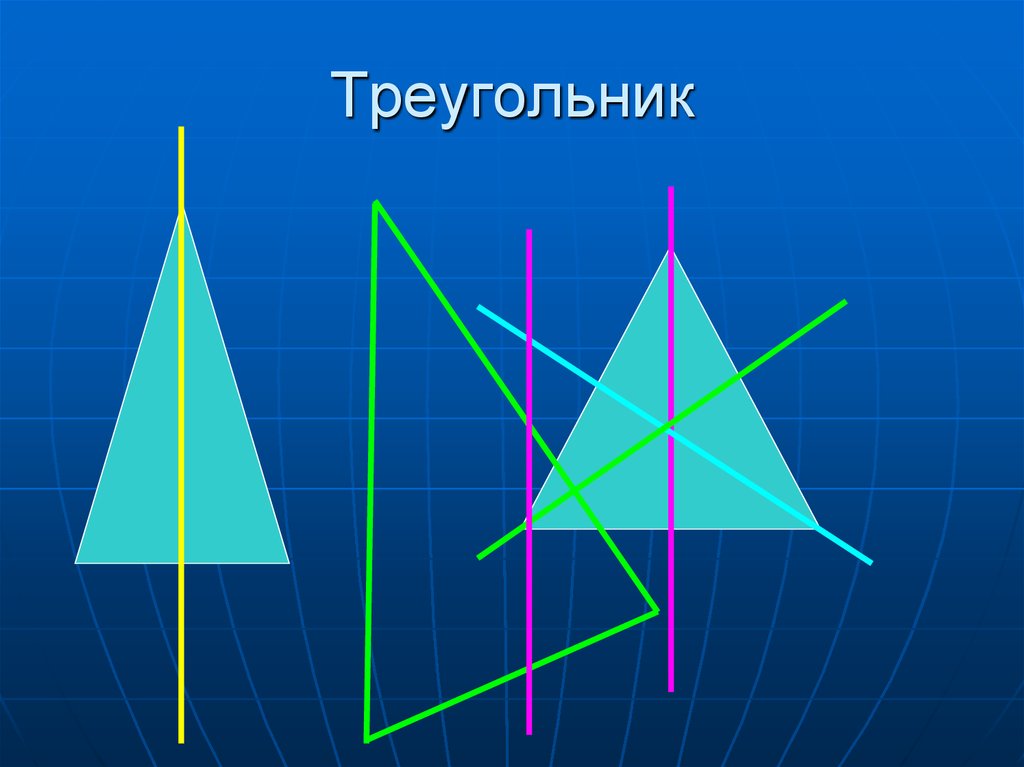
11. Треугольник

12. Прямая имеет бесконечное количество осей симметрий!

Примеры других геометрических
фигур,
имеющие
оси
симметрии:
Какая ещё геометрическая фигура
обладает подобным свойством?
Прямая имеет бесконечное
количество осей симметрий!

13. Фигуры, не обладающие осевой симметрией

Произвольный
треугольник
Параллелограмм
Неправильный
многоугольник

14.

Кроме осевой симметрии
существует еще и ЦЕНТРАЛЬНАЯ
СИММЕТРИЯ.
Она характеризуется наличием центра
симметрии – точки О.
О
При повороте вокруг точки О на 180 градусов фигура
переходит сама в себя.

15.

Задачи
1. Отрезок АВ, перпендикулярный прямой с, пересекает ее в
точке О так, что АО≠ОВ. Симметричны ли точки А и В
относительно прямой с?
2. Прямая а пересекает отрезок МК в его середине под углом,
отличным от прямого. Симметричны ли точки М и К
относительно прямой а?
3. Точки А и В расположены в различных полуплоскостях с
границей р так, что отрезок АВ перпендикулярен прямой р и
делится ею пополам. Симметричны ли точки А и В
относительно прямой р?

16.

Задачи
1. Отрезок АВ, перпендикулярный прямой с, пересекает ее в
точке О так, что АО≠ОВ. Симметричны ли точки А и В
относительно прямой с?
Ответ: нет
2. Прямая а пересекает отрезок МК в его середине под углом,
отличным от прямого. Симметричны ли точки М и К
относительно прямой а?
Ответ: нет
3. Точки А и В расположены в различных полуплоскостях с
границей р так, что отрезок АВ перпендикулярен прямой р и
делится ею пополам. Симметричны ли точки А и В
относительно прямой р?
Ответ: да

17.

4. Изобразите точку А, лежащую в I четверти
координатной плоскости.
Точка В симметрична точке А относительно
оси y.
Точка С симметрична точке В относительно
оси х.
Точка D симметрична точке С относительно
оси у.
Что вы можете сказать:
a.
о точках A и D
b.
о фигуре ABCD
c.
при каком условии ABCD будет квадратом

18.

Ответ:
a.
b.
c.
Точки A и D симметричны
относительно оси х.
ABCD – прямоугольник
Если расстояния от точки А до оси х и
у будут равными

19.

5. Относительно какой из координатных осей симметричны
точки М(7;2) и К(-7;2)?
6. Точки А(5;…) и В(…;2) симметричны относительно оси Ох.
Запишите их пропущенные координаты.
7. Точка А(-2;3), В - симметричная ей точка относительно оси
Ох, точка С – симметричная точке В относительно оси Оу.
Найдите координаты точки С.
8. Точка А(3;1), В – симметричная ей точка относительно
прямой у = х. Найдите координаты точки В.
Проверь себя

20. Проверь себя

5. Ответ: Оу.
6. Ответ: А(5;-2) и В(5;2).
7. Ответ: С(2;-3).
8. Ответ: В(1;3)

21.

9. Для каждого из случаев, представленных на
рисунке, постройте точки А' и В',
симметричные точкам А и В относительно
прямой с.
А
А
В
В
с
А
с
В
с

22.

9. Для каждого из случаев, представленных на
рисунке, постройте точки А' и В',
симметричные точкам А и В относительно
прямой с.
А
А'
А
В'
В
В'
В
с
А'
А
с
В
с
А'
В'

23.

10. Постройте треугольники,
симметричные данным, относительно
прямой с.
с
с

24.

10. Постройте треугольники,
симметричные данным, относительно
прямой с.
с
с

25. Многие предметы окружающего мира имеют ось симметрии или центр симметрии.

Симметрия в природе

26. Симметрия в природе

27. Центральной симметрией обладают различные плоды

28. Центральная симметрия в цветах

29. В архитектуре

30. Бордюры (орнаменты в виде лент)

Применяют маляры и художники при оформлении
комнат, зданий.
Для выполнения этих работ изготавливается
ТРАФАРЕТ.
Маляр передвигает трафарет, переворачивая или
не переворачивая его, обводит контур, повторяя
рисунок, и получает орнамент.

31. Виды бордюров

С параллельным переносом
С зеркальной симметрией
С центральной симметрией

32. Параллельный перенос

33. Бордюр с использованием параллельного переноса и зеркальной симметрии

34. Бордюр с использованием параллельного переноса и центральной симметрии

35. Орнаменты

Кроме рассмотренных линейных
орнаментов существуют плоские
орнаменты, заполняющие
плоскость без промежутков. Такие
орнаменты называют ПАРКЕТАМИ.

36. Пример паркета

37.

Имеют ли буквы русского алфавита ось симметрии?
О
А
В
Х
Е
Э
Г
Р
Н
М
К
Б
И
Ю
Ж
Ф
Л
С
Д
З
Т
УП
Одна ось симметрии
Две оси симметрии

38. Пушкин А.С. «Медный всадник»

…В гранит оделася Нева;
Мосты повисли над водами;
Темнозелеными садами
Ее покрылись острова…
Пушкин А.С. «Медный всадник»

39. Симметричность форм в транспорте

40. Заключение

Симметрию можно
обнаружить почти везде,
если знать, как ее искать.
Многие народы с древнейших
времен владели
представлением о симметрии
в широком смысле – как об
уравновешенности и
гармонии. Творчество людей
во всех своих проявлениях
тяготеет к симметрии.
Посредством симметрии
человек всегда пытался, по
словам немецкого математика
Германа Вейля, «постичь и
создать порядок, красоту и
совершенство».